不同數據處理策略對Chl-a濃度預測精度的影響

(三峽大學 水利與環境學院,湖北 宜昌 443002)

水華是在溫度、光照、營養鹽等環境條件適宜時，藻類大量生長繁殖并富集成一定濃度，導致區域水體變色的現象，是水體富營養化的典型代表。水華暴發易引起明顯的水質變化，嚴重阻隔生態能量的有效循環，破壞水體的生物多樣性，已成為水環境治理中的難題[1]。葉綠素a含量常被作為特征指標用以預測藻類生長暴發，在水體理化性質和生物存量分析指標中占據重要地位[2]。研究藻類水華的暴發機制，分析水體中葉綠素a的時空變化規律，預測水華的時空分布，對水華及其生態影響的預警和防范都具有重大意義[3]。

利用實時監測數據，采用神經網絡對水體中葉綠素a含量進行預測，是水體中葉綠素a含量預測的主要手段之一[4]，得到了廣泛應用[5]，取得了比較有效的預測結果。例如Velo-Suarez等[6]在Andalucia的大西洋沿岸流域實現了對藻類的神經網絡預測模型構建；Guallar等[7]在地中海Alfacs灣建立了對雙鞭毛藻和硅藻的神經網絡預測機制；趙文喜等[8]在中國海河干流完成了基于BP神經網絡的葉綠素a含量預測短時預測研究，皆對相應流域的藻類生長趨勢進行了有效預測。

輸入數據的準確性對神經網絡的預測精度有決定性的影響，但實時監測數據受各種隨機因素影響，會存在異值點、數據缺失、數據不光滑等不符合物理規律的情況[9]，需要對原始監測數據處理，以提高數據質量及預測精度。相關研究表明，不同處理方法對預測精度影響較大。例如王亞宸等[10]在澳大利亞能源市場研究中，采用小波變換處理噪音數據，成功實現了維多利亞州電力負荷以及電價的高精度預測；Iliou等[11]在骨質疏松癥預測案例中，應用了一種基于MLP分類器的新型數據處理方法，達到神經網絡高效分類的目的。但數據處理對基于神經網絡的水體葉綠素a含量預測精度影響方面尚沒有專門研究。

因此，本文在實時監測數據基礎上，分別采用3種異值點處理方法與2種數據光滑方法組合，討論不同數據處理方法對主成分影響，研究神經網絡的輸入參數確定方法，選擇5種神經網絡輸入參數組合，分析不同數據處理方案下神經網絡預測精度，研究樣本數據處理策略對基于神經網絡的葉綠素a預測精度的影響，為提高基于神經網絡的水華暴發預警技術的預警精度提供支撐。

1 數據預處理

1.1 數據來源

研究所采用的數據為研究水域2016年4月下旬到12月監測時段內的pH、氨氮(NH3-N)、電導率(COND)、水溫(WT)、溶解氧(DO)、葉綠素a(Chl-a)、淡水藍綠藻(AFA)、氧化還原電位(ORP)、氣溫(AT)、氣壓(AP)、相對濕度(RH)、降雨(Rainfall)及光強(Lux)13項實時監測數據，數據頻率為每10 min1次。受多種因素影響，數據存在異常值，部分數據缺失，數據連續性及光滑性不足等問題(圖1(a)中，氨氮監測數據存在異常值；圖1(b)中，水溫監測值連續性、光滑性不足)。

圖1 監測數據異常分布示意Fig.1 Unusual distribution of monitoring data

1.2 異常值及缺失值處理

結合本次監測數據的采集頻率及實際分布狀態，本文依次嘗試使用以下3種判據準則進行異常值處理。

(1) 拉依達準則[12](Pauta Criterion)，又稱3σ準則，假設監測數據只存在隨機誤差，對數據計算出標準差σ，隨機誤差在指定概率區間(-3σ,3σ)的分布概率約為99.7%，監測誤差超過指定概率區間就判定為異常值。

(2) 肖維勒準則[13](Chauvenet Criterion)，在監測數據中，臨近時段的n次監測數據，如果某監測值xi與平均值x之差的絕對值大于標準偏差與肖維勒系數之積，則該監測數據為異常值。

(1)

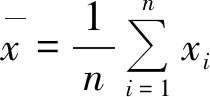
ωn=1+0.4ln(n)

(2)

針對藻類水華數據變幅較大的特性，肖維勒法剔除異常值時樣本數需靈活取值；本文以樣本數500為一組，肖維勒系數ω500=3.20進行異常值判斷。

(3) 格拉布斯準則[14](Grubbs Criterion),監測值對應殘差的絕對值滿足下式時，判定監測值為異常值。

(3)

式中，g(n,a)為格拉布斯臨界系數，與監測樣本數以及顯著水平有關，本文臨界系數取g(100,0.05)=3.17，以樣本數100為一組進行分批檢驗。

本文基于以上3種準則對監測數據進行異常值篩選處理。對于同一監測數據，3種準則選取評判的樣本群體不同(σ=0.398 2，ω500=3.20，g(100,0.05)=3.17)，對應的判定結果亦相異，拉依達準則判定標準最為寬松，格拉布斯準則最為嚴格，肖維勒準則居于兩者之間。此外，若該點監測數據為異常值，則當作缺失值進行處理。

常用缺失值處理方法有個案剔除法、均值替換法、熱卡填充法、回歸替換法、期望最大化法等。本文采用如下方法處理：同一時間點若單項監測數據缺失則采用均值替換法，若同時多項監測數據缺失則采用個案剔除法去除該時間點所有監測數據。

1.3 數據平滑濾波

水體的理化監測指標理論上應是光滑連續變化的，但受監測頻次限制及外界隨機因素干擾，數據光滑性常常不滿足要求，需要利用平滑濾波方法處理。本文在異常值處理的基礎上，分別采用臨近加權平均法、局部多項式回歸法[15]對監測數據平滑。

臨近加權平均法中，以監測點i為計算中心，計算臨近個點k的加權平均值作為監測數據xi對應的平滑值：

(4)

圖2 監測數據平滑效果對比Fig.2 Smoothing effect comparison of monitoring data

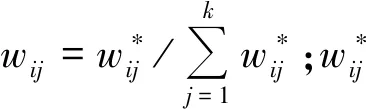
局部多項式回歸，是基于最小二乘法原理在該點擬合回歸的多項式代入值與監測值之差的平方和最小時，確定局部多項式回歸效果最佳，平滑值計算公式如下：

j=-m,…,0,…,+m

(5)

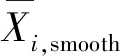
本文采用納什效率系數分析數據平滑效果：

(6)

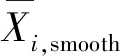
對以拉依達準則、肖維勒準則和格拉布斯準則進行數據異值處理后得到的3組數據，分別進行臨近加權平均、局部多項式回歸處理得到6組數據變換預處理方案，方案中各監測指標以納什效率系數不低于0.985作為平滑標準。各方案既有效消除了數據中的高頻“噪音”影響，同時也盡可能地保持了數據原有的客觀真實性，可以為后續研究提供數據支撐。部分數據平滑前后的對比如圖2所示。

1.4 主成分分析

表1 不同數據處理方案主成分分析結果Tab.1 Principal component analysis results of different data processing schemes

注：1.“3σ”，拉依達準則；“Chauvenet”，肖維勒準則；“Grubbs”,格拉布斯準則；2.“AAv”，臨近加權平均法；“SG”，局部多項式回歸；3.基于特征值0.6；具有Kaiser標準化的正交旋轉法。

以pH、氨氮、電導率、水溫、溶解氧、葉綠素a、氧化還原電位、氣溫、氣壓、相對濕度、降雨及光強標準化后數據進行主成分分析，分析結果擬合度均達到85%以上。顯然，不同數據處理方案得到的主成分也有區別，說明數據處理方案對主成分分析結果有一定影響。但總體而言占據優勢的成分依次為：葉綠素a、氣溫、光強、氣壓、降雨、電導率、相對濕度；可將其作為葉綠素a含量預測輸入參數。

2 基于BP神經網絡葉綠素a預測模型構建

2.1 輸入輸出參數的選擇

由于葉綠素a的含量與藻類的數量密切相關，在一定程度上能夠反映水質狀況，是判斷水體富營養化的重要指標之一[18]，前文主成分分析表明，葉綠素a需為模型輸入參數，才可保證模型的預報精度。需要定義新的輸出參數，以預測下一時刻葉綠素a含量。鑒于此，定義單位時間內葉綠素a含量的變化量為平均生長率GR，用公式表示為

(7)

其中，GR為t1～t2時刻之間的平均生長率。

下一時刻葉綠素a含量，由下式計算：

(8)

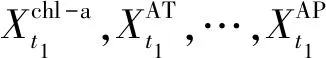
2.2 BP神經網絡結構設置及訓練

適合的BP神經網絡結構設置既能加快收斂速度，也能保證預測精度[19]。本文依據預測誤差最小確定葉綠素a含量預測的BP神經網絡隱含層為2層，隱含層神經元個數為12；隱含層采用learngdm閾值學習函數，輸出層采用purelin傳遞函數；最大迭代次數1 000次，設置0.05的步長。有效數據11 000組，其中8 000組作為訓練集，2 000組作為測試集，1 000組作為預測集。葉綠素a含量預測的BP神經網絡結構圖如圖3所示。

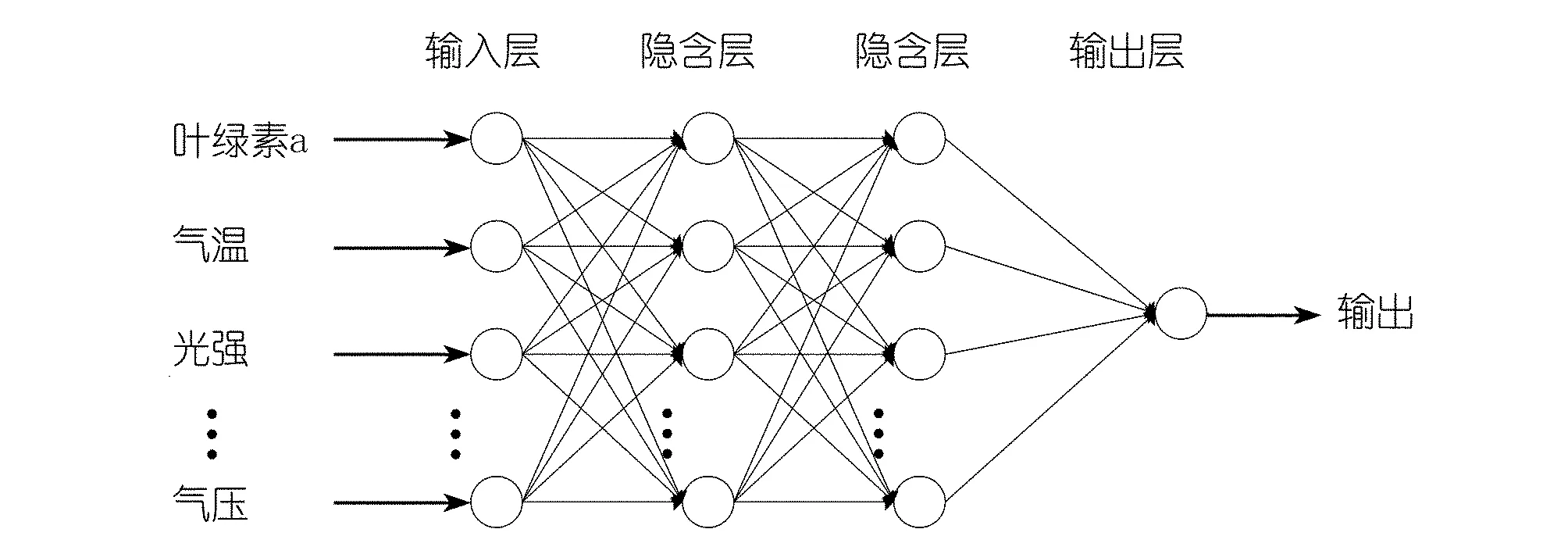
圖3 BP神經網絡結構Fig.3 BP neural network structure

研究不同數量輸入參數組合對神經網絡預測精度的影響，當參數輸入數量相同時，以預測精度最好的組合作為該輸入參數下的最優組合。以格拉布斯準則異常值處理組合局部多項式回歸平滑處理數據為例，不同輸入參數下葉綠素a含量預測值分布對比見圖4。不同數量的最優輸入參數組合，對葉綠素a含量均有較好的預測精度，說明影響葉綠素a含量變化的因子間不是相互獨立的，各因子間存在交織作用。因此，關注主要影響因子，精簡預測模型輸入是提高葉綠素a含量預測效率的可行途徑。

不同數量的最優參數組合預測精度如表2所示，對比主成分分析結果可發現，7參數下輸入參數的最優組合與主成分分析結果相同，當輸入參數減少時，去除的輸入參數為主成分分析結果中權重最小的因子，主成分分析結果可用于指導神經網絡輸入參數選擇；神經網絡預測精度隨著輸入參數的增加而提高，將所有監測參數(13個)當作輸入參數時，預測精度最高，可達0.994，相比4參數輸入的0.986，預測精度有所提高，但提高程度有限。其中，4、13參數葉綠素預測效果對比如圖5所示。

圖4 不同參數輸入下葉綠素a含量分布Fig.4 Distribution of Chlorophyll-a content under different parameters input

表2 不同輸入參數組合的平均生長率預測精度Tab.2 Average growth rate prediction accuracy of different input parameter combinations

3 數據處理對預測精度影響

將3種異值點處理方法與2種數據光滑方法組合，結合原始數據，得到了7組數據處理方案，與5種輸入參數數量方案組合，共可得到35種組合方案。針對每種數據處理方案，進行主成分分析，根據各影響因子權值，由小到大剔除輸入參數，對BP神經網絡訓練，得到不同數據處理方案及不同輸入參數組合下的預測精度結果，如表3所示。

采用原始數據進行預測時，預測精度普遍不高，如圖6所示，預測精度不隨輸入參數增加而增加，說明原始數據存在干擾項，影響神經網絡預測精度。

對比原始數據方案與數據處理后方案，在輸入參數數目相同情況下，對數據進行處理可顯著提高神經網絡的預測精度，但不同的數據處理方法對其預測精度的提高程度不同。在采用臨近加權平均法對數據進行平滑處理的條件下，不同數據異值處理方法對預測精度提高效果明顯，但預測精度與輸入參數數量間相關性較差，不同數據異值處理方法優劣無法確定，但以拉依達準則處理后得到的預測精度最高，為0.938。在采用局部多項式回歸方法對數據進行平滑處理的條件下，不同數據異值處理方法對預測精度提高顯著，預測精度與輸入參數數量間相關性強，以格拉布斯準則處理效果最好，肖維勒準則處理效果較差。

圖5 4，13參數輸入的葉綠素a含量預測效果Fig.5 Comparison of Chlorophyll-a content prediction results with 4 and 13 input parameters

表3 不同數據處理方案的預測精度Tab.3 Prediction accuracy of different data processing schemes

注：不同數據處理方案得到的主影響因素不同，相應不同方案的最優輸入參數組合不同。

整體而言，采用局部多項式回歸方法對數據進行平滑處理，對預測精度改善優于臨近加權平均方法，如圖7、8所示，采用局部多項式回歸的葉綠素a含量預測誤差，整體波動幅度更小。格拉布斯準則異值處理組合局部多項式回歸法平滑數據，在不同輸入參數數量下均可達到最佳預測結果。該方案可以將以葉綠素a、氣溫、光強及氣壓4項因素下的葉綠素a預測精度從原始數據的0.800提高至0.986，同比提高23.25%。

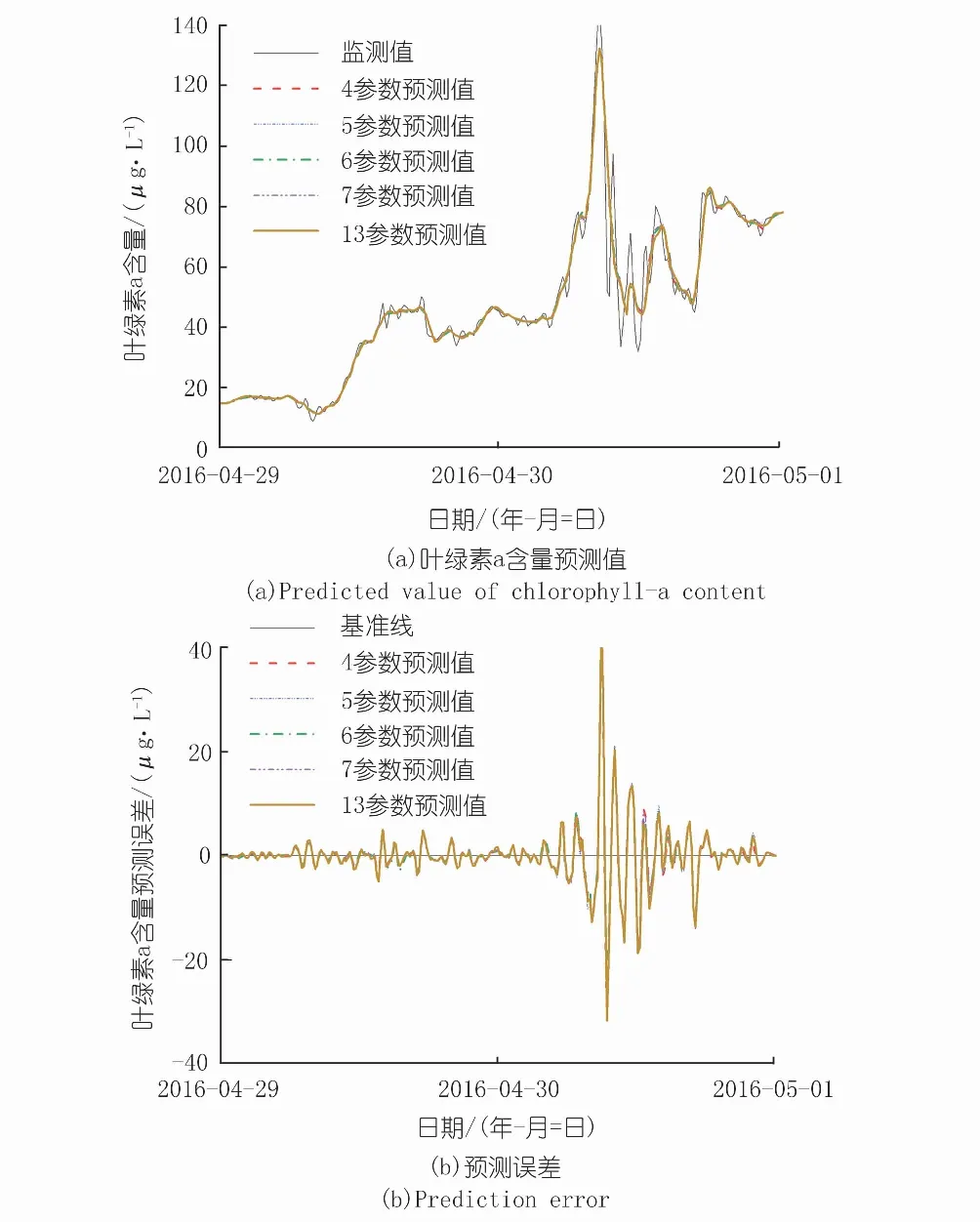
圖6 原始數據的不同輸入參數預測效果Fig.6 Different input parameters′ prediction effects with initial data

圖7 臨近加權平均法的葉綠素a含量預測效果Fig.7 Prediction effect of chlorophyll-a content by weighted average method

圖8 局部多項式回歸法的葉綠素a含量預測效果Fig.8 Prediction effect of chlorophyll-a content by local polynomial regression method

4 結 論

本文對神經網絡的訓練數據進行預處理，建立了35種組合方案，對基于BP神經網絡葉綠素a含量平均生長率進行預測，對比分析預測結果，評估數據處理對基于神經網絡的葉綠素a預測精度的影響。得到如下結論。

(1) 主成分分析方法可為BP神經網絡輸入參數選擇和簡化提供極為重要的參考。

(2) 利用數據處理技術對基礎監測數據進行處理，可顯著提高基于神經網絡的葉綠素a含量預測精度。

(3) 不同的數據處理方案對基于神經網絡的葉綠素a預測精度影響幅度不同；以格拉布斯準則進行異值處理，組合局部多項式回歸法進行數據平滑，是本研究的最佳數據處理方案。

(4) 本研究方法的內在作用機理，需要在對數據處理前后幅值、頻譜等數據特征變化進行深入研究后明確。