基于人口和GDP的主要水污染物排放量預測
——以秦皇島市為例

(同濟大學 土木工程學院，上海 200092)

1 研究背景

嚴重的環境污染問題已經成為社會經濟發展的阻礙。如今保護環境成為了人們的共識,節能減排已經正式作為一項重要工作進入國家和地方經濟發展總量規劃[1]。國家“十三五”規劃中指出：我們要下更大決心,用更大氣力,采取更有效的政策措施,切實將節能減排工作推向深入。并且制定了節能減排目標：到2020年,全國萬元國內生產總值能耗比2015年下降15%。在眾多污染問題當中水污染問題尤為嚴重。根據環保部2017年環境公報:全國地表水1 940個水質斷面(點位)中,Ⅰ～Ⅲ類水質斷面(點位)1 317個,占67.9%；Ⅳ～Ⅴ類462個,占23.8%；劣Ⅴ類161個,占8.3%[2]，水質情況不容樂觀。預測水污染物排放量對制定合理的節能減排方案是十分必要的。秦皇島市作為沿海城市之一,近年來水體污染也很嚴重,Ⅰ～Ⅲ類、Ⅳ～Ⅴ類、劣Ⅴ類水質斷面分別占48.1%，44.6%和7.3%[3]。秦皇島市水體污染高于全國平均污染,本文針對秦皇島市水體污染問題展開研究。

水污染主要包括生活污染、工業污染等[4]。生活污染中CODCr(化學需氧量)、TN(總氮)、TP(總磷)計算與人口總數關系密切,工業污染中CODCr、TP與GDP(國內生產總值)密切相關。為了能夠預測未來水污染物排放量,首先就需要對人口和GDP進行相應預測。因此,本文首先依據秦皇島市1990～2015年人口和GDP對2020年人口和GDP進行了預測,繼而研究生活污染與人口關系,工業污染與GDP關系,最終按照排污系數法預測得出2020年秦皇島市主要水污染排放總量。

2 2020年人口預測

秦皇島市統計局統計得出了1990～2015年全市人口數據,統計結果如圖 1所示。2015年年末秦皇島全市常住人口307.32萬人,比上年末增加0.87萬人；出生人口2.71萬人,人口出生率為8.81‰；死亡人口1.81萬人,人口死亡率為5.88‰；人口自然增長率為2.93‰,比上年下降2.05‰。全市城鎮化率52.02%,比上年提高2.38%,比全省平均水平高2.69%。秦皇島市人口總體上升,基本呈指數趨勢增加。因為第五次人口普查將很多原來沒有常住人口登記卡的居民登記在冊,所以2010年人口數據出現陡升。為了預測2020年主要水污染物排放量,就需要對人口進行相應分析并做出合理預測。

圖1 1990～2015年秦皇島市人口數量Fig.1 Population of Qinhuangdao in 1990～2015

對于人口數據的預測,以往的研究者多次采取了馬爾薩斯(Malthus)模型,取得了較好的擬合結果。張金明等人在北京市人口預測中利用馬爾薩斯模型,在低方案下相對誤差為1.58%[5]；何春利用馬爾薩斯模型預測廣州市人口,相對誤差最大值僅為0.14%[6]；徐金等基于馬爾薩斯模型對黑龍江省人口進行預測,2007年預測值與實際結果相比誤差僅為0.2%[7]；陳麗云等利用馬爾薩斯模型對玉溪市人口進行預測, 2017年實際值與預測值比較,預測相對誤差為7.4%[8]；金鑫等利用馬爾薩斯模型分析預測了甘肅省人口數據,根據實測值得出相對誤差僅為0.4%[9]；朱列、王宇等利用馬爾薩斯模型對廣西和新疆三地州人口進行預測，取得了較好的結果[10-11]。因此,基于眾多成功的應用,本文亦采用馬爾薩斯模型預測秦皇島2020年的人口。

英國人口學家馬爾薩斯(Malthus)于1798年提出了馬爾薩斯人口模型。其建模思路如下：假設人口的(相對)增長率是常數,人口預測采用指數增長函數公式(1)。

馬爾薩斯模型公式：

Pn=P0(1+R)n

(1)

式中,P0為初始人口,Pn為第n年人口,R為年增長率,本研究為方便用n表示年份,取1990年n=0。基于馬爾薩斯指數模型,利用Origin軟件采用指數模型擬合原始數據,得到結果如圖 2所示。

擬合后人口數據與原始統計數據基本趨勢相一致,最大相對誤差為1.6%,平均相對誤差為0.8%,能夠反映人口增長趨勢。首先依據擬合結果得出公式(1)中參數為：P0=245.428 5萬人,R=0.009 02。利用擬合得到的公式預測未來5 a人口數據如表1所示。根據秦皇島統計局最新人口數據：2016年市常住人口數為309.46萬人,與預測數據對比誤差僅為1.6%。說明擬合結果基本與實際增長趨勢相一致。

圖2 指數模型擬合人口Fig.2 Exponential model fitting population

表1 2016～2020年人口預測Tab.1 Predicted population in 2016～2020萬人

3 2020年GDP預測

GDP(國內生產總值)是國民經濟核算的核心指標,也是衡量一個國家或地區總體經濟狀況的重要指標，是一個國家經濟實力的象征。合理準確預測GDP對國家經濟研究十分重要。目前GDP預測模型主要有：多元回歸模型、生產函數模型、灰色理論模型、人工神經網絡模型、時間序列模型[12]。其中時間序列模型理論發展迅速且應用廣泛,許多研究者采用此模型預測GDP已經取得了很好的結果。魏寧在陜西省GDP預測中模擬值與實測值最大相對誤差為5.7%[13]；李守麗在鄭州市GDP預測中最大相對誤差為2.4%[14]。根據原序列是否平穩以及回歸中所含部分的不同,時間序列模型包括自回歸(AR)模型、移動平均(MA)模型、自回歸移動平均(ARMA)模型和自回歸積分滑動平均模型(ARIMA)[15]。

ARIMA模型是將非平穩時間序列轉化為平穩時間序列,然后將因變量僅對它的滯后值以及隨機誤差項的現值和滯后值進行回歸所建立的模型。ARIMA(p,d,q)方法就是將數據進行d次差分后轉換成ARMA(p,q)模型。ARMA模型原理是認為時間序列值Yt是過去干擾值εt-1、現在干擾值εt、過去觀測值Yt-i以及常數c的線性組合,具體表達式如公式(2)所示。

(2)

式中，p表示自回歸系數,q表示移動平均系數,φi為自回歸參數,θi為移動平均參數。由于GDP數據基本呈遞增趨勢,屬于非平穩時間序列,前3個模型只能應用于平穩時間序列,故GDP研究多采用ARIMA模型。

3.1 原始GDP及其一階差分

秦皇島市統計局提供的1990～2015年GDP統計數據如圖 3所示,可以看出2005年之前GDP平穩增長,2005年之后經濟快速增長。

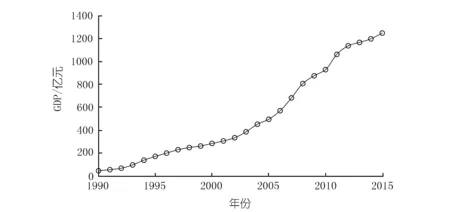
圖3 1990～2015年秦皇島市GDPFig.3 GDP of Qinhuangdao in 1990～2015

為了能夠合理進行預測,要求分析數據序列基本平穩,即需要對GDP進行平穩性分析。采用以ARIMA為基礎的時間序列模型,首先需要對GDP進行差分,使差分數據滿足平穩性要求。當顯著性水平均大于0.05時,則序列滿足白噪聲序列要求,可認為滿足平穩性要求。

秦皇島市1990～2015年GDP依時間變化關系如圖3所示,顯著性水平均為0,不滿足顯著性水平均大于0.05,序列是非白噪聲序列,不可應用于計算。需要進一步對數據進行處理,直到找到一個能夠滿足白噪聲序列的數學模型。

按照公式(3)～(5)對GDP取對數、一階差分、二階差分。

y(t)=lnGDP(t)

(3)

(4)

(5)

式中，GDP(t)表示按時間變化的GDP數據,為方便計算取1990年t=0,因GDP數據是逐年遞增,故取Δt=1。GDP一階差分數據如圖4所示,可以看到始終在0以上,不具有平穩性。

3.2 GDP二階差分

二階差分(Dy2)依時間關系可以發現Dy2數據是在0上下波動,基本滿足平穩性要求,見圖5，顯著性水平如表2所示。

由表 2相關系數分析可以看到顯著性水平均大于0.05,說明序列是白噪聲序列,所建立的數學模型能夠應用于預測計算。下一步利用Dy2進行未來GDP的預測。

圖4 GDP一階差分的時變過程Fig.4 Time-varying process of the first order difference of GDP

圖5 GDP二階差分的時變過程Fig.5 Time-vavring process of the second order difference of GDP

表2 Dy2顯著性水平分析Tab.2 Significance level analysis of GDP

3.3 GDP預測

首先利用Eviews8.0軟件處理二階差分數據,對1991～2015年二階差分值進行擬合,最后得到二階差分預測數據圖像如圖6所示,可以看出擬合結果較平穩。利用預測出的二階差分數據根據公式(3)～(5)轉換計算得出GDP,統計得出GDP實測值與預測值比較如圖7所示。

GDP預測值與實測值基本趨勢相一致,前期是模型的收斂期,后面10 a最大相對誤差為11.4%,平均相對誤差為7.3%。后面5 a最大相對誤差為8.1%,平均相對誤差為6.2%。誤差分析說明后期結果擬合較好。根據驗證后的模型可以預測得出2016～2020年GDP數據如表3所示。秦皇島統計局統計得出2016年GDP為1339.54億元,預測值與實際值相對誤差為5.6%,預測結果較好。總體來說,該模型能較好模擬1990-2015年GDP數據。采用此方法預測得到的2020年秦皇島GDP為1 420.14億元。

圖6 預測與實際GDP二階差分的比較Fig.6 Comparison of second order difference of predicted and real GDP

圖7 預測與真實的GDP比較Fig.7 Comparison between prediction and real GDP

表3 2016～2020年GDP預測Tab.3 Predicted GDP in 2016～2020億元

4 主要水污染物排放量預測

水污染主要可以分為生活水污染、工業水污染、農業水污染以及水土流失等[16]。其中生活水污染CODCr，TN，TP的計算和人口相關,工業污染CODCr，TP與經濟指標GDP相關。前面預測的2020年秦皇島人口和GDP為水污染預測提供了基礎。

4.1 生活污染

估計生活污染產生量的方法分為兩種：排污系數法和綜合污水法。本文采用排污系數法來計算。黃秀清等在樂清灣和象山港海洋環境容量及污染物總量控制研究[17-18]中,將生活污染分為農村生活污水、城鎮生活污水和人糞尿污染。秦皇島生活污染排放系數統計如表4所示。

表4 生活污染排放系數Tab.4 Emission coefficient of domestic pollution kg/(a·人)

前文預測得到2020年秦皇島人口321.32萬人,根據《秦皇島市國民經濟和社會發展“十三五”規劃綱要》預計2020年秦皇島城鎮化率65%,可以得出城鎮人口208.86萬人,農村人口112.46萬人,得到2020年生活污染排放量如表5所示。

表5 生活污染排放量Tab.5 Emission load of domestic pollution t

4.2 工業污染

工業污染的排放與經濟增長是相關的,且二者關系滿足庫茲涅茨曲線[19]。環境庫茲涅茨曲線(Environment Kuznets Curve簡稱EKC)是20世紀90年代初由美國經濟學家Grossman與Krueger提出的,表明環境污染與經濟增長兩者之間呈現“倒U形”曲線關系,指出在經濟發展過程中,環境污染物排放量先是隨經濟增長快速上升,達到一個峰值后隨經濟增長再下降。王佳等[20]根據環境庫茲涅茨曲線對秦皇島環境污染進行了分析研究，得出秦皇島工業廢水排放量與人均GDP公式(6)。

Y=-4 984.24+13 949.67X-5 949.06X2+810.85X3

(6)

式中,X為人均GDP，萬元；Y為工業廢水排放量，萬t。

前文預測得到的2020年秦皇島市人口預計為321.32萬人,全市總GDP為1 420.14億元,則人均GDP為4.42萬元/a。依據公式(6)可以得出2020年秦皇島工業廢水排放量為12.657億t。

根據《中華人民共和國污水綜合排放標準》(GB8978-1996),城鎮污水處理廠出水排入地表水Ⅳ、Ⅴ類(GB3838)功能水域或海水三、四類(GB3097)功能海域,執行污水二級排放標準,CODCr日排放量不超過100 mg/L,TP日排放量不超過3 mg/L。

按照最高允許排放濃度計算2020年工業廢水中水污染物排放量,可以得到CODCr年排放量為10 467.70 t,TP年排放量為314.03 t。

4.3 水污染物排放總量預測

本文水污染預測包含生活污染、工業污染,主要預測項目包括CODCr，TN，TP。由人口預測數據計算得出生活污染排放量,由GDP預測數據計算得出工業污染排放量,最后綜合考慮二者共同作用統計得到主要水污染物排放總量如表6所示。

表6 水污染物排放總量Tab.6 Total load of water pollutants t

5 結 語

秦皇島市人口與GDP均呈逐年遞增的態勢,分別采用馬爾薩斯模型和以ARIMA為基礎的時間序列模型進行人口和GDP的預測。以2020年人口和GDP為基礎,按照排污系數法預測主要水污染物排放量，主要結論如下。

(1) 采用馬爾薩斯模型預測近5 a秦皇島人口數,2016年人口預測值與實測值的相對誤差僅為1.6%,2020年人口預測值為321.32萬人。

(2) 采用以ARIMA為基礎的時間序列模型預測近5 a秦皇島GDP,2016年GDP預測值與實測值的相對誤差為5.6%,2020年GDP預測值為1 420.14億元。

(3) 采用排污系數法預測生活污水污染物排放量,采用環境庫茲涅茨曲線并結合《中華人民共和國污水綜合排放標準》(GB8978-1996)預測工業污水污染物排放量,預測秦皇島2020年生活和工業污染物CODCr排放量為74 317.170 t,TN排放量為2 488.946 t,TP排放量為21 672.160 t。本文的預測結果具有良好的參考價值,可以為相關部門制定節能減排方案提供科學依據。