輸氣管道環(huán)焊縫表面裂紋管道極限載荷計算方法

王 旭 帥 健

中國石油大學（北京）安全與海洋工程學院

0 引言

有關(guān)統(tǒng)計資料顯示，自2010年以來我國至少發(fā)生了管道環(huán)焊縫失效事故12起，其中強力組對、焊接缺陷和材料韌性不達標是造成環(huán)焊縫失效的主要原因。因此針對在役含缺陷管道特別是環(huán)焊縫缺陷的適用性評估是一項必要且十分迫切的工作，既能從事故源頭減少管道事故的發(fā)生，也能充分發(fā)揮管材性能，避免不必要的開挖、換管等開支[1]。

失效評定圖方法（Failure Assessment Diagram，F(xiàn)AD）作為目前評估管道缺陷的主流方法之一，最早由英國中央電力局（Central Electricity Generating Board，CEGB）提出[2]，而后由美國電力研究所（Electric Power Research Institute，EPRI） 提 出的“含缺陷油氣容器及管道的完整性評定規(guī)程”（簡稱EPRI評定規(guī)程）進一步完善[3]。EPRI提出的管道缺陷的J積分估算方法及相應的J積分理論提高了FAD評估方法的實用性及準確性，對于小口徑及低強度鋼管具有較好的覆蓋性及適用性。Lei和Budden[4]最早基于等效應力—應變的思想，結(jié)合EPRI方法，提出了考慮焊縫非等匹配下的平板中心裂紋J積分估算公式，并通過試驗與有限元的方式對公式進行修正。Kim等[5-6]基于EPRI方法考慮內(nèi)壓和彎曲載荷情況下，給出了一定范圍內(nèi)的管道和裂紋幾何尺寸的全塑性J積分解，進而給出了極限載荷的計算方法。Song等[7]提供了中心貫穿表面裂紋板的錯匹配極限載荷以及J積分估算方法。Hertelé等[8]針對焊縫結(jié)構(gòu)的材料不均勻性，提出了基于中心裂紋拉伸試件的非均勻焊縫的修正J積分計算方法。Paredes和Ruggieri[9]擴展了EPRI手冊中J積分全塑性解的適用范圍。Souza和Ruggieri[10]基于EPRI和參考應力法，研究了一定范圍裂紋幾何尺寸、焊接失配程度下的彎曲載荷作用下管道環(huán)向表面裂紋J積分的求解方法。國內(nèi)學者帥健和辛艷霞[11]提出了一種基于失效評定圖的可靠性分析方法去確定油氣管道彈塑性斷裂失效概率。孫亮等[12]在EPRI理論的基礎(chǔ)上，導出以等效原場應力為參量的塑性J積分計算方法，白永強等[13-14]擴展了EPRI手冊的適用范圍等。

綜上所述，含缺陷結(jié)構(gòu)的塑性J積分作為管道缺陷評估方法中的關(guān)鍵參數(shù)，國內(nèi)外學者針對其塑性解已有一定的研究基礎(chǔ)，但是現(xiàn)階段這些國內(nèi)外研究成果針對目前主流的大口徑、薄壁、高鋼級的管道研究應用尚有不足，公式適用范圍有限抑或是預測結(jié)果過于保守或激進，筆者基于目前國內(nèi)已規(guī)模化應用的X80級鋼管材料性能，考慮裂紋尖端處的應力奇異性，利用有限元軟件ANSYS建立了含表面裂紋的管道環(huán)焊縫有限元模型，在EPRI方法的基礎(chǔ)上考慮焊縫匹配系數(shù)的影響，研究環(huán)焊縫表面裂紋驅(qū)動力J積分的計算方法，并在此基礎(chǔ)上分析含裂紋管道的極限載荷影響因素，可為現(xiàn)役管道的安全評價及完整性管理提供參考。

1 含表面裂紋的管道有限元模型

1.1 幾何模型及參數(shù)

在工程實際問題中，管道環(huán)焊縫缺陷在承受軸向拉伸載荷時最為危險，本文建模即考慮此種情況，即建立受拉伸載荷作用下的含環(huán)向表面裂紋的管道模型，如圖1所示。

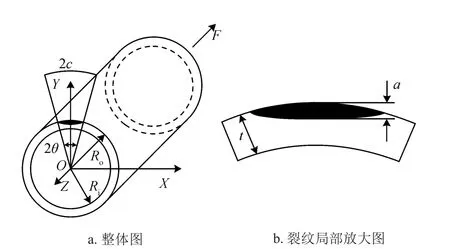
圖1 含環(huán)向裂紋的管道受拉伸載荷的幾何模型圖

建模參數(shù)參考GB/T 9711—2017《石油天然氣工業(yè)管線輸送系統(tǒng)用鋼管》[15]中關(guān)于X80級鋼管的拉伸試驗要求，設(shè)計系數(shù)取0.72，按GB 50251—2015《輸氣管道工程設(shè)計規(guī)范》[16]的壁厚公式計算壁厚，具體信息如表1所示。

表1 管道模型的尺寸及材料參數(shù)表

1.2 有限元模型

采用二維奇異單元經(jīng)裂紋路徑掃掠生成三維奇異單元的方法，考慮裂紋尖端的奇異性，進而構(gòu)建管道環(huán)向的外表面半橢圓裂紋。即采用ANSYS推薦的PLANE183單元生成裂尖單元面，用SOLID186單元通過掃掠形成整個裂紋前緣。為減小計算量，提高計算精度，同時考慮到管道模型具有對稱性，故采用1/4模型進行建模，對裂紋區(qū)域網(wǎng)格進行加密處理，同時遠離裂紋區(qū)域適當稀疏，建立的1/4含環(huán)向表面裂紋的管道模型如圖2所示。

為了研究裂紋深度和長度以及管材應變硬化性能對裂紋驅(qū)動力的影響，采用3種不同硬化指數(shù)的管材進行建模，計算了3種不同長度及深度的缺陷對裂紋J積分的影響。同時將1/4管道模型長度設(shè)為500 mm，以減少端部效應對計算結(jié)果造成的影響[17]。

1.3 模型驗證

為驗證所建立含缺陷管道模型計算結(jié)果的準確性，將模型計算得到的J積分通過公式（平面應力）轉(zhuǎn)換為應力強度因子（KI），從而與標準中提供的KI進行對比。英國標準協(xié)會（British Standards Institution，BSI）發(fā)布的BS 7910-2015 《金屬結(jié)構(gòu)缺陷驗收評定方法導則》中給出了管道外表面環(huán)向裂紋的應力強度因子求解方法[18]：

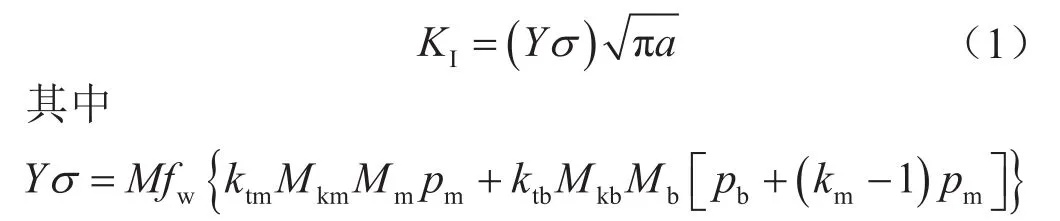
式中pm表示薄膜應力，MPa；pb表示彎曲應力，MPa；M表示焊縫匹配系數(shù)；其余符號均為無量綱的計算參量，可通過查附錄得其表達式或數(shù)值，其中下標為b的代表彎曲應力相關(guān)參量，本文計算中均取0。

圖3為在軸向拉伸載荷作用下即pm＝0.6σ0（σ0表示屈服強度，取表1數(shù)據(jù)），多組不同缺陷尺寸下的管道環(huán)向裂紋最深處應力強度因子計算值的對比情況。經(jīng)計算誤差均在5%以內(nèi)，說明所建立的含環(huán)向表面裂紋的管道有限元模型計算結(jié)果較為準確可信。

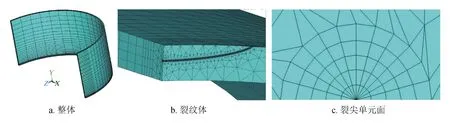
圖2 有限元模型圖

圖3 有限元計算的KI值與BS 7910標準中的KI值比較圖

2 環(huán)焊縫表面裂紋因子

EPRI方法將J積分的計算分為彈性部分Je和塑性部分Jp。其中，彈性部分Je可由式（平面應力情況下）得到。塑性部分表達式為：

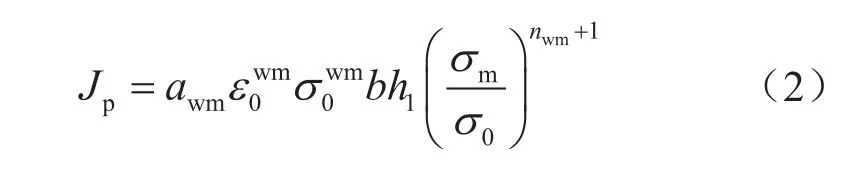
式中b表示非裂紋部分的尺寸，mm，b=t-a；σm表示管道遠端施加的拉伸載荷，MPa；σ0表示屈服強度，MPa；ε0表示σ0對應的應變；h1表示無量綱因子；其余帶wm上標或下標的符號表示焊接金屬（Weld Metal）的對應性質(zhì)。

由式（2）可以看出，h1因子為EPRI方法估算J積分的關(guān)鍵參數(shù)之一，其數(shù)值與管道環(huán)焊縫表面裂紋尺寸以及管材應變硬化性能有關(guān)。由式（2）可得：

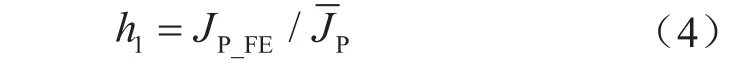
其中 JP_FE＝J-Je。

2.2 考慮焊縫匹配系數(shù)的有限元模型

為研究管道環(huán)焊縫的焊縫匹配系數(shù)對含缺陷管道的影響，考慮選用兩種較為明顯的焊縫強度錯匹配情況：20%的低匹配（指焊縫的屈服強度比母材屈服強度低20%，M=0.8）和20%的高匹配（指焊縫的屈服強度比母材屈服強度高20%，M=1.2）。并在此基礎(chǔ)上對前述的有限元模型進行材料設(shè)置。參考本文參考文獻[19]對X80級鋼管的材料性能研究，采用R-O模型來描述材料的應力應變性能，將有限元模型的管道材料設(shè)置如表2所示，表中n值為R-O模型的參數(shù)，代表材料的冪硬化指數(shù)。

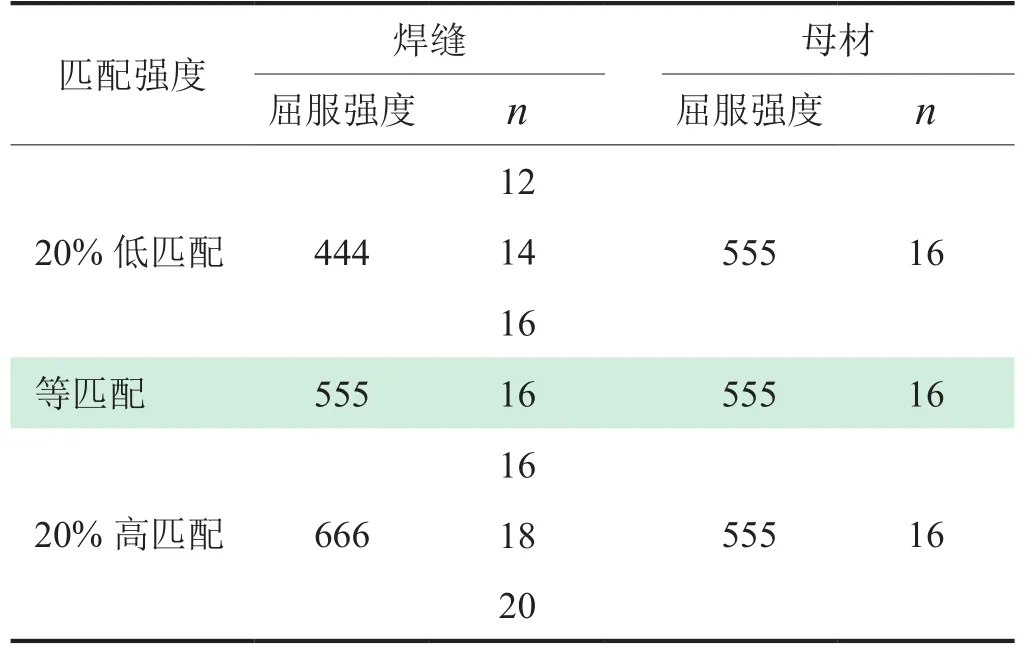
表2 含環(huán)焊縫裂紋缺陷的管道模型材料設(shè)置表

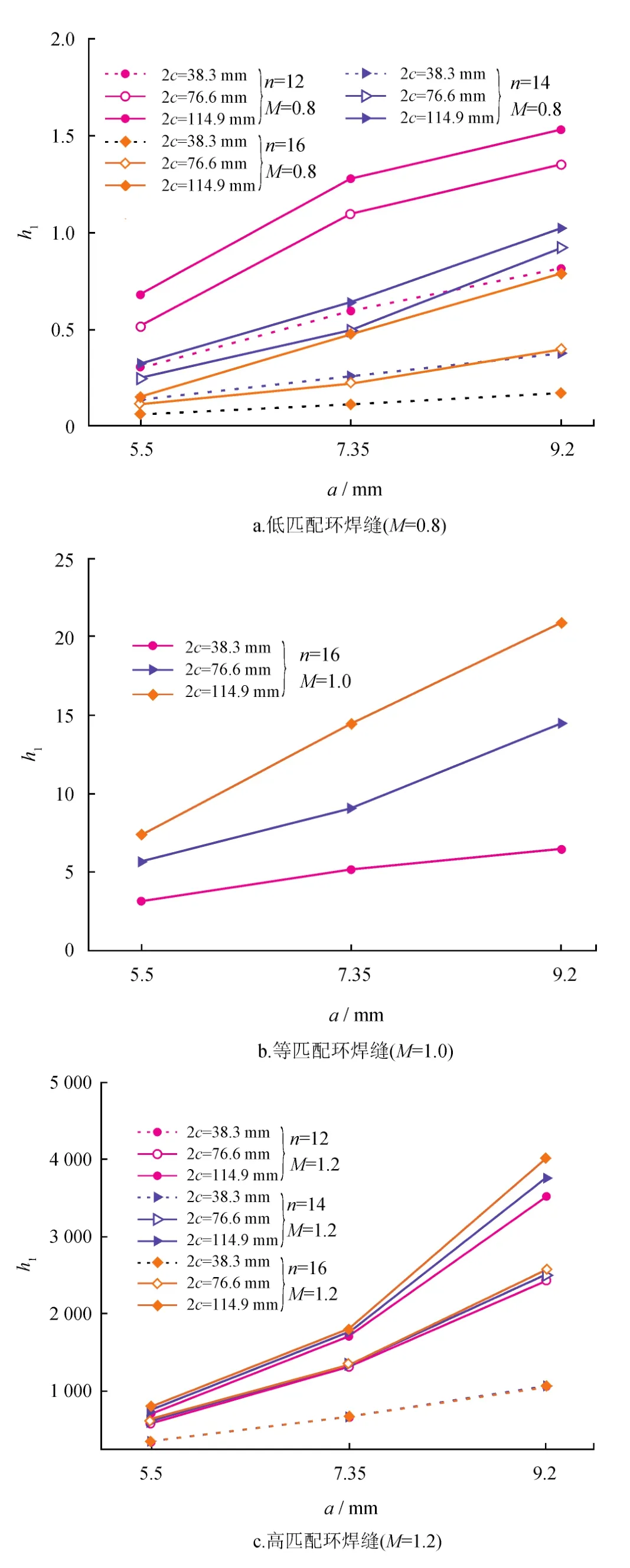
圖4 不同匹配情況下的環(huán)焊縫h1因子隨裂紋尺寸的變化圖

基于考慮焊縫匹配系數(shù)的有限元模型以及上述式（4）即可實現(xiàn)對不同情況下的h1因子進行求解。考慮不同的焊縫匹配系數(shù)及不同裂紋尺寸情況，將所得結(jié)果繪制如圖4所示。

由圖4的結(jié)果總體來看，h1因子隨著裂紋的長度、深度以及材料硬化指數(shù)及焊縫匹配系數(shù)的增大而增加，匹配系數(shù)越高，h1因子對裂紋的尺寸越敏感；而裂紋尺寸較大時，材料硬化指數(shù)對h1因子影響也越來越明顯。根據(jù)h1因子隨裂紋的長度及深度的變化情況，可將h1因子描述為裂紋尺寸的函數(shù)，裂紋長度和深度分別用來表示，采用多元多項式進行擬合，即

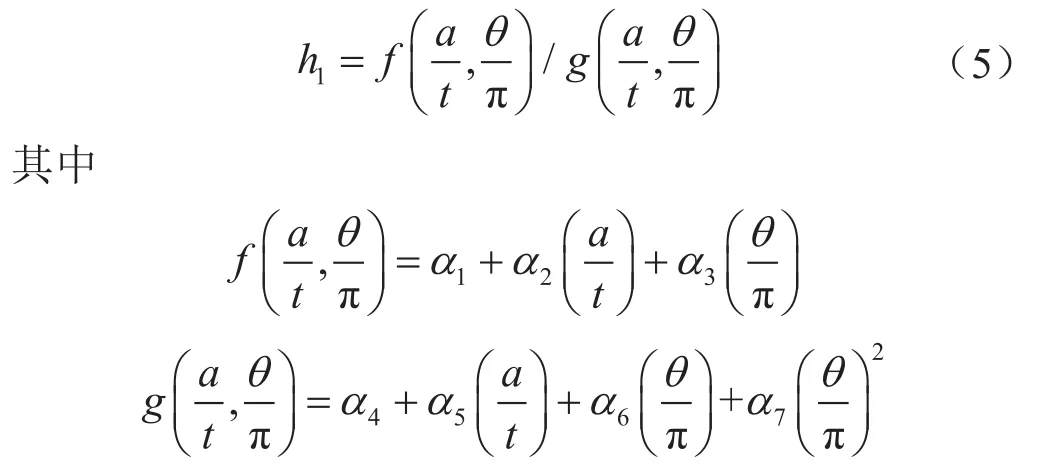
式中α1～α7表示參數(shù)，其值采用非線性最小二乘法萊文貝格-馬夸特法（Levenberg-Marquardt Method）擬合得到，列于表3中，適用范圍為0.01≤0.03、0.3≤0.5。

根據(jù)表3參數(shù)及式（5）擬合出h1因子函數(shù)，與有限元計算得到的h1因子值進行對比，計算所得誤差情況如圖5所示。可以看出低匹配和等匹配情況下部分誤差較大，在M=0.8、n=14時，出現(xiàn)最大的擬合誤差在14%左右，但是整體平均誤差在5%以內(nèi)，說明本文擬合的適用于X80管道的環(huán)焊縫表面裂紋J積分計算公式具有較高的精度，能夠?qū)崿F(xiàn)較大裂紋尺寸范圍、且考慮焊縫匹配系數(shù)的含管道環(huán)焊縫裂紋J積分運算，滿足工程計算的需要。

表3 h1因子多項式擬合的參數(shù)值表

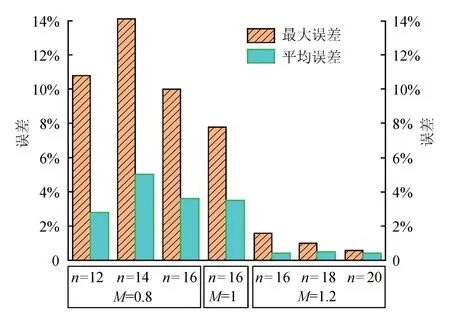
圖5 h1因子擬合誤差圖

3 基于J積分的極限載荷分析

基于塑性全量理論發(fā)展的塑性極限載荷分析理論目前已成為多個標準計算含環(huán)向裂紋管道的極限載荷的主要推薦方法之一，其中應用最為廣泛的是凈截面垮塌準則，該準則假設(shè)含環(huán)向裂紋的管道處于塑性極限狀態(tài)時，管道承受載荷發(fā)生變形時的裂紋凈截面上的應力為均布的屈服應力[20]，塑性極限載荷反映了含缺陷管道的極限承載能力。BS 7910中將含缺陷管道極限載荷定義為：

式中Lr表示載荷比；pL表示管道軸向極限載荷，MPa；Ft表示極限載荷系數(shù)；σwm表示焊縫材料的屈服強度，MPa；σref表示參考應力，其大小與缺陷位置及尺寸有關(guān)，MPa。

上式中Lr應滿足：

式中εref表示參考應變，其數(shù)值等于真應力為參考應力 σref＝Lrσ0時對應的真應變。

由式（6）、（7）結(jié)合上述建立的有限元模型，即可求得任意載荷作用下的J和Je，進而求得對應載荷作用下的Lr，具體求解過程本文不再贅述，現(xiàn)將不同匹配強度下的含缺陷管道極限載荷計算情況繪制如圖6所示。

由圖6可以看出，在低匹配、等匹配或高匹配情況下，含缺陷管道的極限載荷均隨著裂紋尺寸的增加而降低，隨著材料硬化指數(shù)的增大而增大；而在管道裂紋缺陷尺寸及材料硬化指數(shù)一定時，高匹配的含缺陷管道的極限載荷明顯要高于低匹配或等匹配的情況，某些情況下高匹配的含缺陷管道的極限載荷甚至要高于管道母材本身的屈服極限載荷。說明對含環(huán)焊縫中心線處表面裂紋的X80管道而言，高強匹配是明顯優(yōu)于低匹配的。

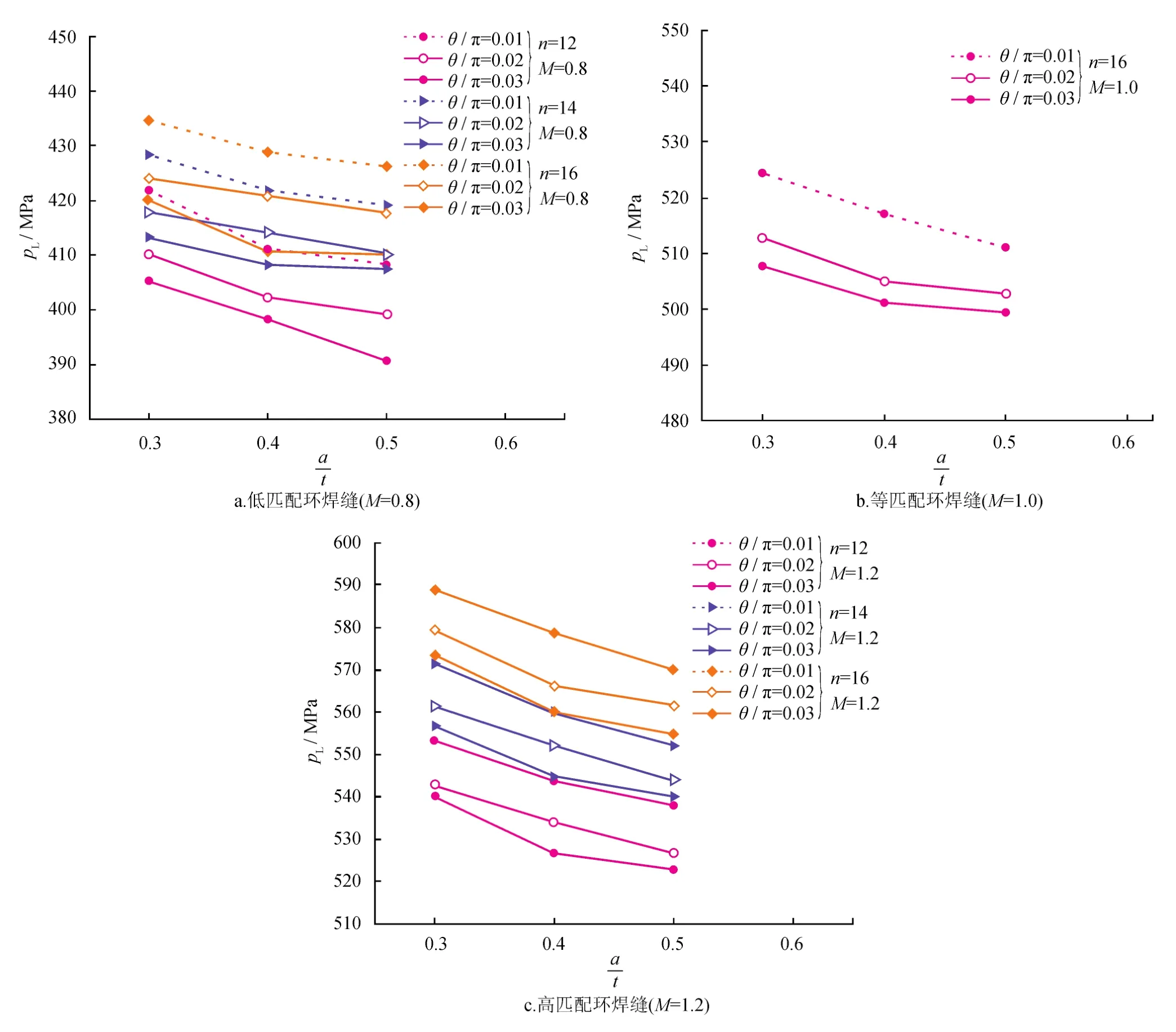
圖6 不同匹配情況下的含缺陷管道的極限載荷圖

根據(jù)含缺陷管道的極限載荷的隨裂紋尺寸、材料硬化系數(shù)、匹配強度等參數(shù)的變化情況，現(xiàn)根據(jù)式（6）求出極限載荷系數(shù)（Ft），并將其轉(zhuǎn)變?yōu)榱鸭y深度和長度的函數(shù)，采用多項式進行擬合，即可在特定強度匹配水平和材料應變硬化性能的情況下快速求出含缺陷管道的極限載荷，F(xiàn)t系數(shù)的表達式為：

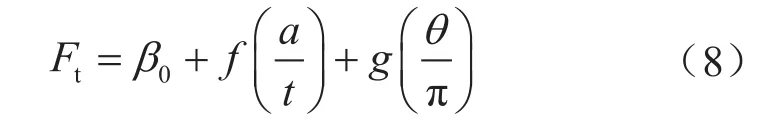
其中

式中β0～β6表示參數(shù)，其值采用非線性最小二乘法萊文貝格-馬夸特法（Levenberg-Marquardt Method）進行擬合而得，將得到的參數(shù)列于表4，本公式的適用范圍為。

據(jù)式（8）及擬合系數(shù)即可快速計算含缺陷管道的極限載荷，并與有限元結(jié)果進行對比，擬合公式的計算誤差見圖7，從中可以看出無論最大誤差還是平均誤差均沒有超過0.5%。故認為本文擬合的含缺陷管道極限載荷計算公式具有較高的精度，能夠滿足工程計算的需求，實現(xiàn)考慮焊縫匹配系數(shù)及材料硬化指數(shù)的含環(huán)焊縫缺陷管道的極限載荷快速計算。

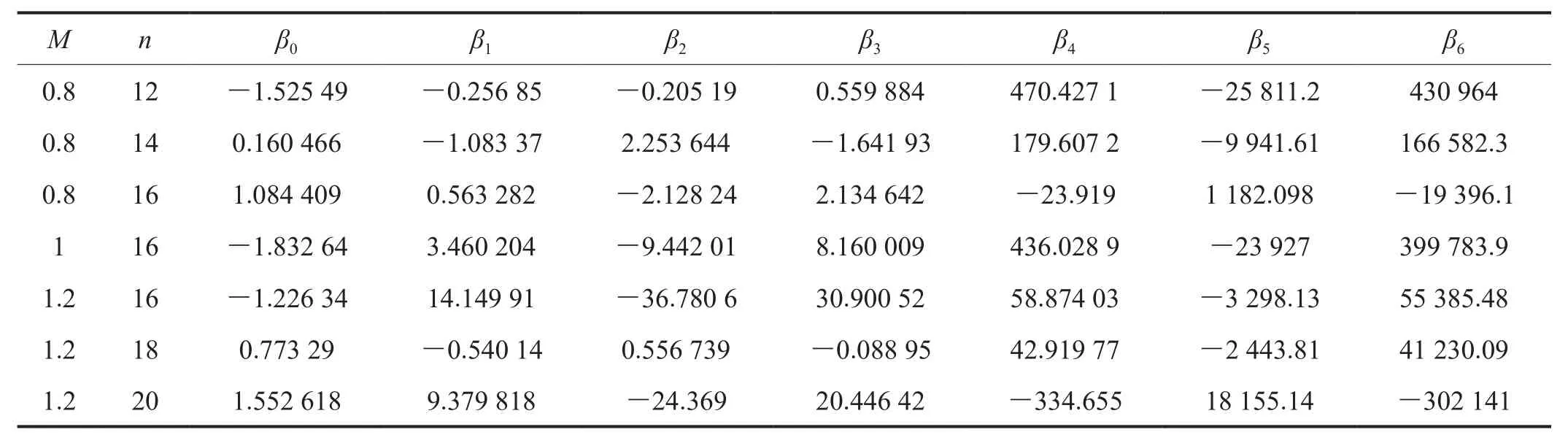
表4 Ft系數(shù)多項式擬合的參數(shù)值表

圖7 Ft系數(shù)的擬合誤差圖

4 結(jié)論

1）建立了含環(huán)向表面裂紋的管道有限元模型，與BS 7910中提供的應力強度因子值的對比誤差均在5%以內(nèi)，說明所建立的含環(huán)向表面裂紋的管道有限元模型計算結(jié)果較為準確可信。

2）含缺陷管道的裂紋J積分會隨著裂紋的長度、深度以及材料的硬化指數(shù)（n）、焊縫匹配系數(shù)（M）的增加而增加；M越大，J積分對裂紋的尺寸越敏感；而裂紋尺寸較大時，材料的n對J積分的影響也越來越明顯。

3）在低匹配、等匹配或高匹配情況下，含缺陷管道的極限載荷會隨著裂紋尺寸的增加而降低，隨著材料硬化指數(shù)的增大而增大；而在管道裂紋缺陷尺寸及材料硬化指數(shù)一定時，高匹配的含缺陷管道的極限載荷明顯要高于低匹配或等匹配的情況，說明對含環(huán)焊縫中心線處表面裂紋的X80管道而言，高強匹配是明顯優(yōu)于低匹配的。

4）在對含缺陷管道J積分及極限載荷影響因素分析的基礎(chǔ)上，提出了針對特定匹配系數(shù)和材料硬化指數(shù)情況下的，能夠?qū)崿F(xiàn)J積分及極限載荷快速計算的公式，與有限元計算結(jié)果對比表明，公式計算結(jié)果具備較高的精度，可以滿足工程計算需要。