帶兩個參數的非均勻三次三角B樣條曲線

汪 凱，張貴倉，王 敏

?

帶兩個參數的非均勻三次三角B樣條曲線

汪 凱，張貴倉，王 敏

(西北師范大學數學與統計學院，甘肅 蘭州 730070)

為了使構造的三次三角非均勻B-樣條曲線在具備形狀可調性、高階連續性、精確表示橢圓等性質的同時還具有變差縮減性，構造了一類具有全正性的帶2個參數的非均勻三次三角B-樣條基函數，進而進行曲線構造。首先假設待構造的非均勻三次三角B-樣條基在每一個節點處具有2連續且具有單位性，進而確定基函數的表達式；然后給出了基函數具有全正性等重要性質；最后給出了非均勻三次三角B-樣條曲線的定義，并證明了其具有變差縮減性等重要性質，還證明了曲線在取特殊參數值時具有(2n–1)階連續。實例表明，本文構造的曲線有效解決了傳統方法存在的問題，適合于幾何設計。

非均勻B-樣條；高階連續性；全正性；參數；變差縮減性

經典B-樣條方法是在保留Bézier方法優點的同時，克服了其由于整體表示帶來不具有局部性質的缺點以及解決在描述復雜形狀時帶來的連接問題下提出的。一直以來，B-樣條方法都是計算機輔助幾何設計(computer aided geometric design，CAGD)的主流方法，但B-樣條方法存在控制頂點確定的情況下，曲線較為固定的不足，雖然曲線曲面的非均勻有理B-樣條(non-uniform rational B-spline，NURBS)解決了該問題，但是其權因子的問題至今無法解決。為此，針對該類問題，不少學者提出了帶形狀參數的擬B-樣條曲線[1-14]，使其在保留傳統B-樣條方法基本性質的同時，且具有一定的形狀可調性。

目前，關于經典B-樣條方法的改進有很多，且以均勻B-樣條為主，但該類方法并未能在幾何造型設計中得到廣泛的應用，其主要存在3點不足：①在多項式空間框架下構造的曲線不能精確表示圓錐曲線；②只保留了經典B-樣條方法的一些基本性質，如幾何不變性、凸包性、仿射不變性等，像變差縮減性、保凸性等重要性質往往被忽略；③此類方法大都可以達到2連續，且已經滿足了大部分的幾何工業設計的需要，但對于部分高階連續的幾何設計，這些方法就很難達到其要求了。而改進方法大都只解決了其中1個或者2個問題，未能進行全面考慮。

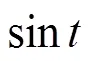
1 基的定義與性質

1.1 基礎知識

1.2 非均勻三次三角B-樣條基的構造

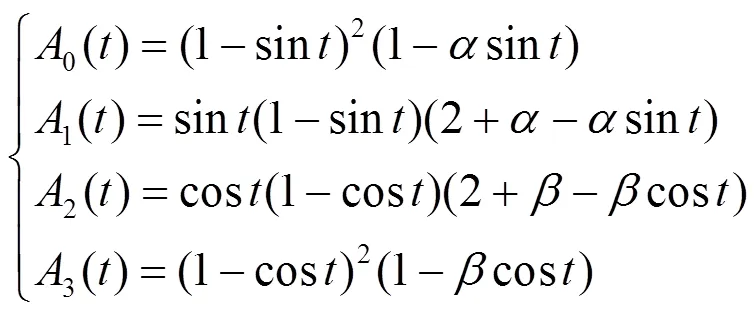
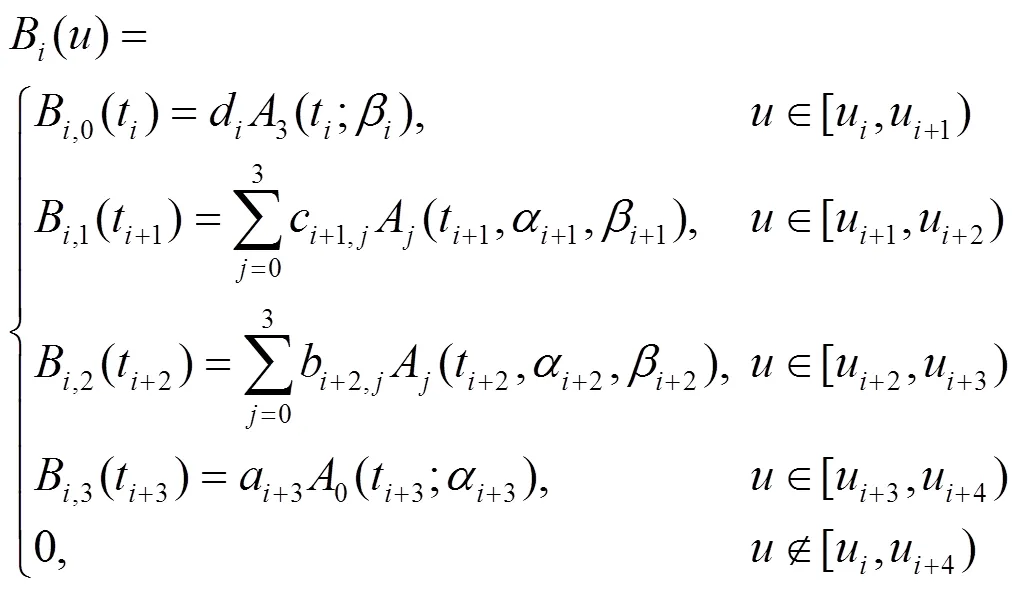
對于等距節點，稱CT-B樣條基B()為均勻CT-B樣條基，相應的節點矢量稱為等距節點矢量。對于非均勻節點，稱CT-B樣條基B()為非均勻CT-B樣條基，相應的節點矢量稱為非等距節點矢量。圖1給出了均勻CT-B樣條基在不同形狀參數下的圖像。

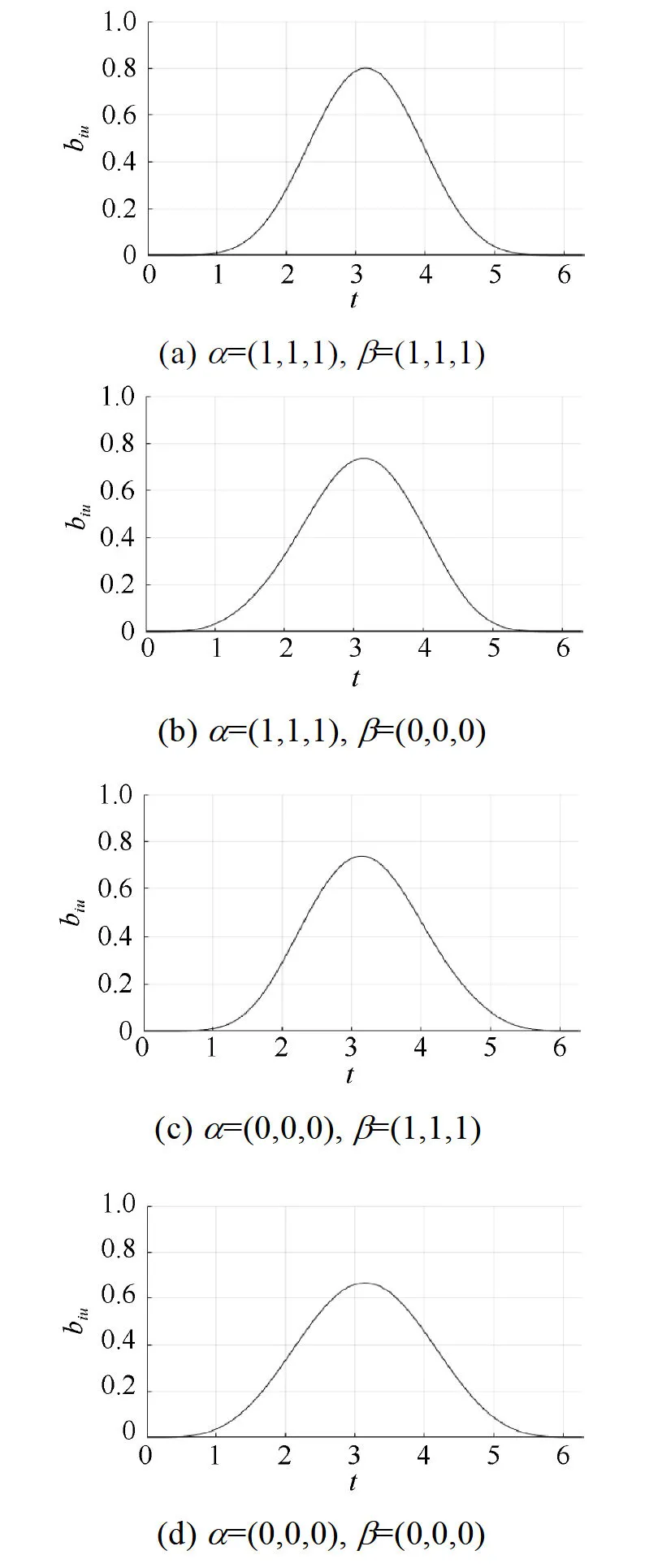
圖1 均勻CT-B樣條基

由圖1計算可得到如下引理。

(1)a+b0+i0=1；

(2)b1+c1=1；

(3)b2+c2=1；

(4)b3+c3+d=1；

(5)b=c+1,0；

(6)b+2,0=c+1,3；

(7)b+2,3=c+3；

1.3 非均勻CT-B樣條基的性質

證畢。

其中，

顯然，基函數(1)的一階導數滿足式(3)的形式；

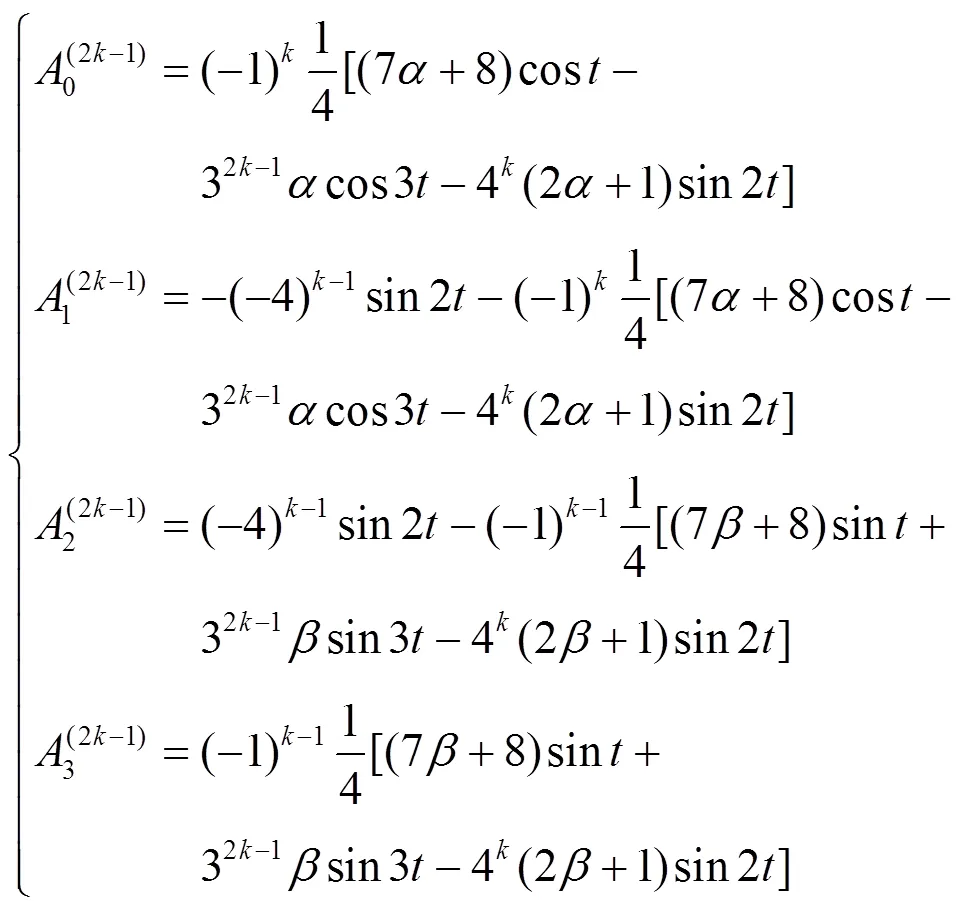
再直接對式(4)進行二次求導，整理可得

2 非均勻三次三角B樣條曲線

2.1 曲線的定義與性質

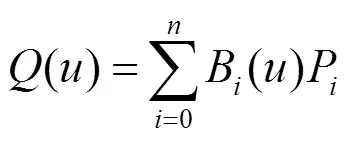
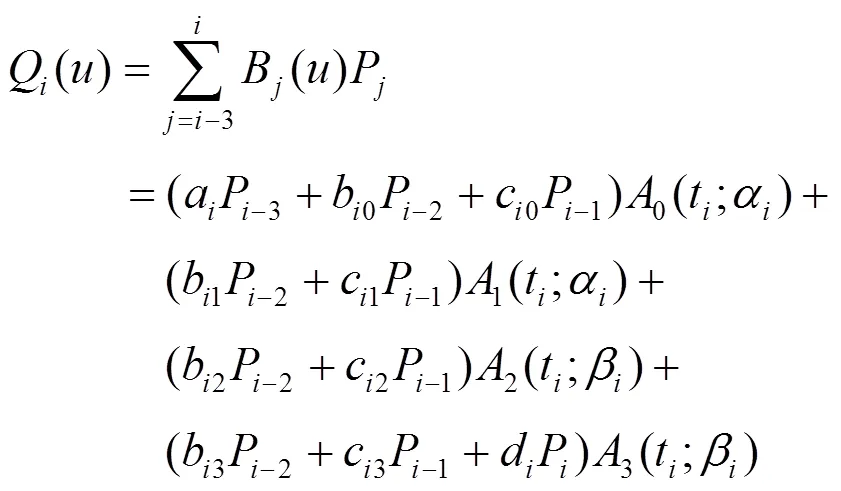
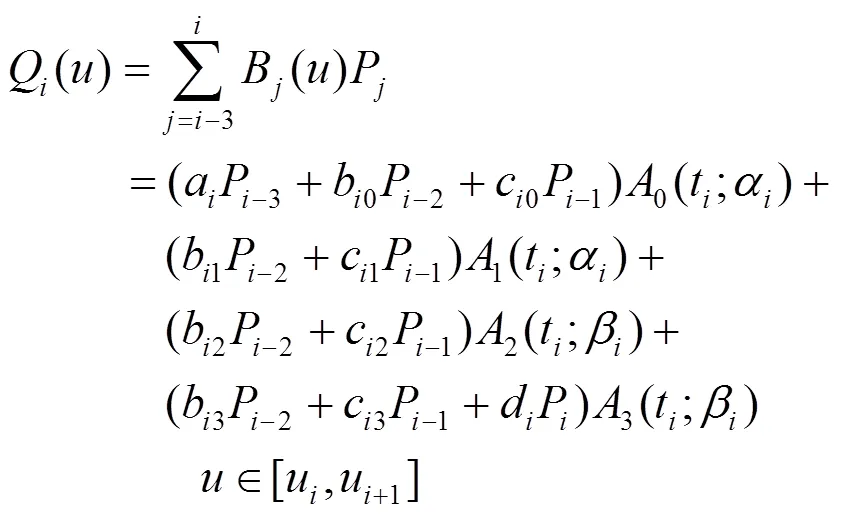
和

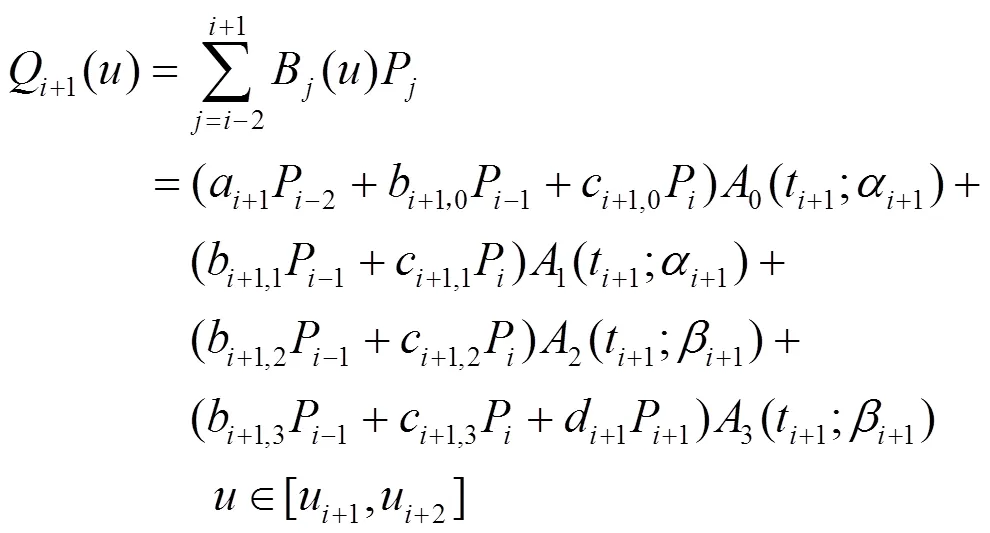
則

證明：由定理6和定理7有

2.2 局部調整性質

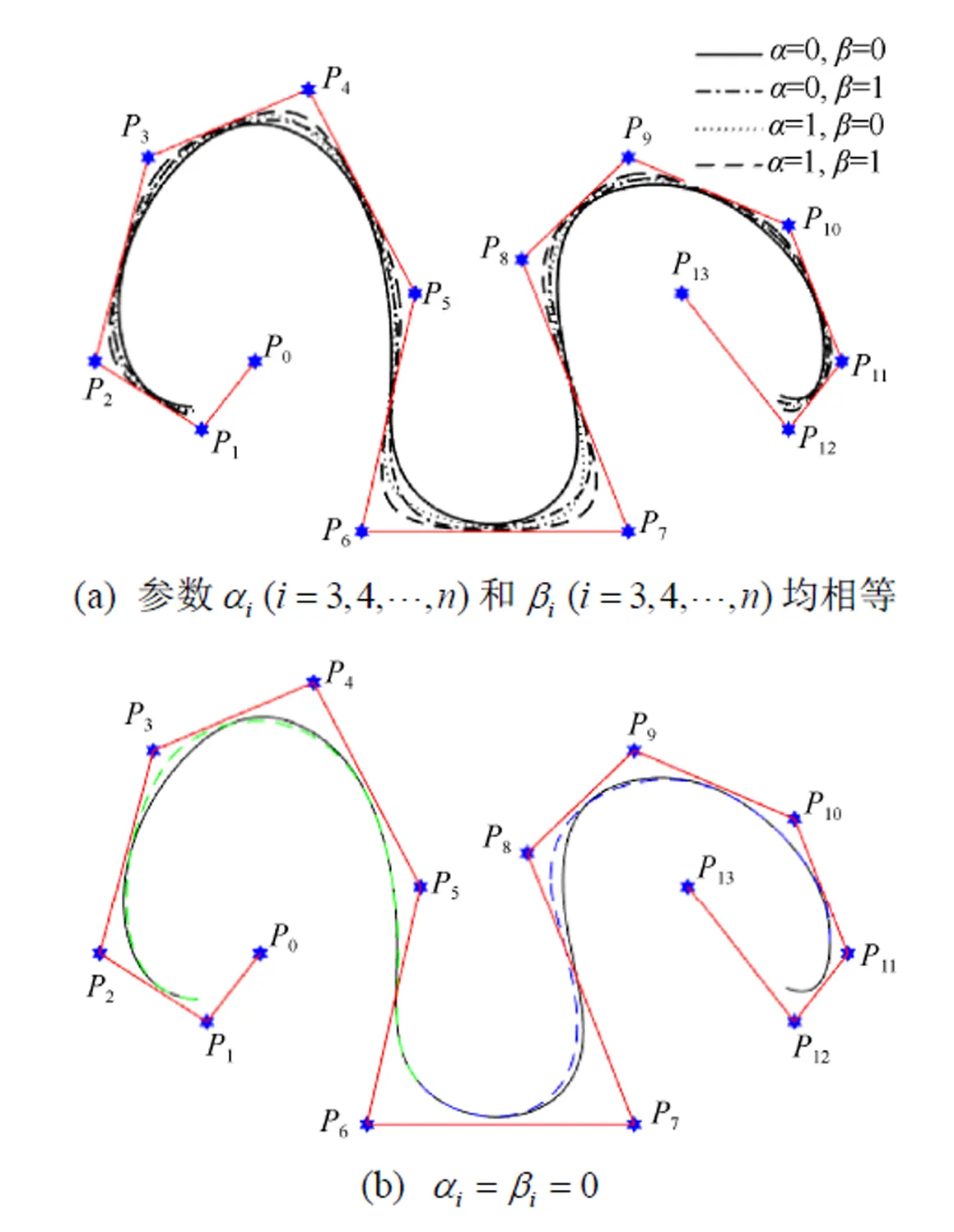
圖2 CT-B樣條曲線

2.3 橢圓的精確表示

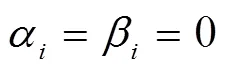
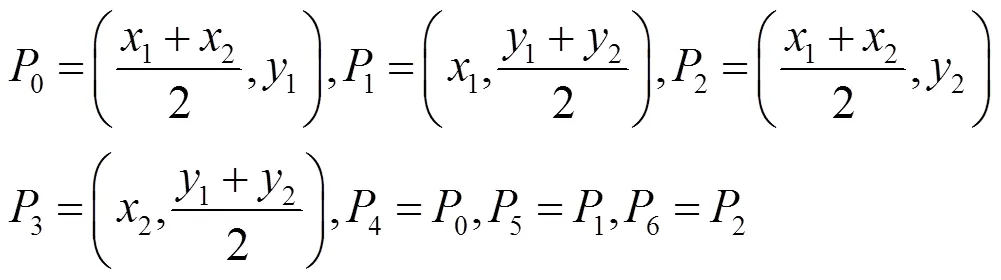
其中，，CT-B樣條曲線可精確表示一個完整的橢圓；當時，CT-B樣條曲線可精確表示1個整圓(圖3)。

3 結束語

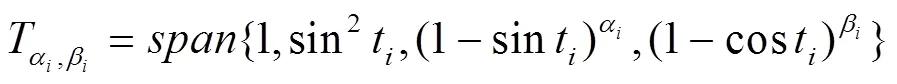
[1] 張貴倉, 耿紫星. 三次均勻B樣條曲線的α擴展[J]. 計算機輔助設計與圖形學學報, 2007, 19(7): 884-887.

[2] 韓旭里, 劉圣軍. 三次均勻B樣條曲線的擴展[J]. 計算機輔助設計與圖形學學報, 2003, 15(5): 576-578.

[3] 王文濤, 汪國昭. 帶形狀參數的均勻B樣條[J]. 計算機輔助設計與圖形學學報, 2004, 16(6): 783-788.

[4] 吳曉勤, 韓旭里. 帶形狀參數的二次三角Bézier曲線[J]. 工程圖學學報, 2008, 29(1): 82-87.

[5] 師利紅, 張貴倉. 三次TC-Bézier曲線的新擴展[J]. 計算機工程與應用, 2011, 47(4): 201-204.

[6] LYU Y G, WANG G Z, YANG X N. Uniform hyperbolic polynomial B-spline curves [J]. Computer Aided Geometric Design, 2002, 19(6): 379-393.

[7] LIU X M, XU W X, GUAN Y. Hyperbolic polynomial uniform B-spline curves and surfaces with shape parameter [J]. Graphical Models, 2010, 72(1): 1-6.

[8] 鄔弘毅, 左華. 多形狀參數的二次非均勻雙曲B-樣條曲線[J].計算機輔助設計與圖形學學報, 2007, 19(7): 876-883.

[9] 李軍成, 宋來忠, 劉成志. 集多種特性的三次三角偽B樣條[J]. 中國圖象圖形學報, 2016, 21(4): 425-433.

[10] 嚴蘭蘭, 韓旭里. 高階連續的形狀可調三角多項式曲線曲面[J]. 中國圖象圖形學報, 2015, 20(3): 427-436.

[11] 邢燕, 樊文, 檀結慶, 等. 一類C2連續的單位四元數插值樣條曲線[J]. 計算機輔助設計與圖形學學報, 2017, 29(1): 45-51.

[13] 李軍成, 嚴蘭蘭, 劉成志. 形狀可調的5次組合樣條及其參數選擇[J]. 中國圖象圖形學報, 2017, 22(2): 197-204.

[14] 嚴蘭蘭, 韓旭里. 三次均勻B樣條曲線的保形擴展[J].計算機應用研究, 2017, 34(1): 295-301.

[15] 朱遠鵬. 基函數中帶形狀參數的幾何造型理論與方法研究[D]. 長沙: 中南大學, 2014.

[16] HAN X L, ZHU Y P. Total positivity of the cubic trigonometric Bézier basis [J]. Journal of Applied Mathematics, 2014(3): 1-5.

[17] CARNICER J M, PENA J M. Total positive bases for shape preserving curve design and optimality of B-splines [J]. Computer Aided Geometric Design, 1994, 11(6): 635-656.

Non-Uniform Cubic Trigonometric B-Spline Curve with Two Shape Parameters

WANG Kai, ZHANG Gui-cang, WANG Min

(School of Mathematics and Statistics, Northwest Normal University, Lanzhou Gansu 730070, China)

To make the extended cubic trigonometric non-uniform B-spline curves possess not only shape adjustability, high order continuity, and exact representation of ellipse, but also variation diminishing, a class of non-uniform cubic trigonometric B-spline basis functions based on totally positivity is constructed. Firstly, we assume that the non-uniform cubic trigonometric B-spline basis functions to be constructed have2continuity and partition of unity at each knot, and accordingly the expressions of the basis functions are determined. Then it is proved that the basis functions have total positivity and other important properties. The definition of non-uniform cubic trigonometric B-spline curves are given, and its important properties such as variation diminishing are proved. It is also proved that the curve has(2n–1)order continuity when taking special parameter values. The example shows that the curve constructed in this paper effectively solves the problems existing in the traditional method and is suitable for geometric design.

non-uniform B-spline; high order continuity; totally positivity; parameter; variation diminishing

TP 391

10.11996/JG.j.2095-302X.2019020395

A

2095-302X(2019)02-0395-08

2018-08-22；

2018-12-18

國家自然科學基金項目(61861040)；甘肅省科技資助項目(17YF1FA119)；蘭州市科技計劃項目(2018-4-35)

汪 凱(1993-)，男，安徽六安人，碩士研究生。主要研究方向為計算機圖形學。E-mail：616688448@qq.com