考慮大孔隙下滲的HBV模型及其在山洪預報中的應用

崔逸凡，呂海深,2,3，朱永華,2，蘇建賓

(1.河海大學 水文水資源學院，江蘇 南京 210098；2.河海大學 水文水資源與水利工程科學國家重點實驗室，江蘇 南京 210098；3 河海大學 全球變化與水循環國際合作聯合實驗室，江蘇 南京 210098)

1 研究背景

近年來，由于全球氣候變化導致極端天氣頻發，突發性暴雨頻率快速增加，洪水災害已成為造成人民生命財產損失的重大災害，嚴重制約著廣大地區社會經濟的發展[1]。據統計，中國是一個洪水災害頻發的國家，洪水災害造成的死亡人數占自然災害死亡人數的比例呈上升趨勢，對人民生命安全造成了嚴重危害[2]，因此洪水的防治已迫在眉睫。洪水防治主要包括工程措施和非工程措施，其中，洪水預報作為洪水防治最重要的非工程措施已上升到國家戰略層面。目前，對于大江大河的洪水預報技術已經比較成熟，而受限于對山洪形成機制認識不全面、山區小流域水文資料匱乏和降水預報精度不高等因素，小流域山洪預報的精度往往并不能滿足實際需要。水文模型模擬是進行洪水預報的重要方法，但是由于小流域山洪具有歷時短強度大、陡漲陡落等特點，許多模型對于小流域山洪的模擬精度并不高，容易出現洪峰模擬較差以及洪水過程線模擬不準確等現象。

HBV模型是由瑞典國家水文氣象局(SMHI)在20世紀70年代開發的水文預報模型[3]，目前已被廣泛應用于全球40多個國家的數百個流域的洪水預報和水資源評估中。近年來，HBV模型在國內也已經得到廣泛應用，如趙彥增等[4]利用HBV模型對淮河官寨流域進行了模擬研究，徑流過程模擬結果比較理想，可在國內推廣應用；王有恒等[5]利用HBV模型在白龍江流域進行了模擬研究，得出HBV模型能較好地模擬洪水對降水的響應過程。然而HBV模型對土壤層的處理較為簡單，僅將土壤層分為上、下兩層，其物理過程并不明確。在植被發育區，由于土壤脹縮、動物活動、植被發育及植被根系死亡等，大孔隙普遍存在。大孔隙雖然在土壤總孔隙中所占比例較小，但由大孔隙引發的優先流對降雨的快速入滲和土壤水的快速補給產生了重要貢獻[6]，大孔隙的存在還會改變坡面尺度地表徑流、壤中流和地下徑流的形成過程和比例，提早地下徑流的出流時間和增加地下徑流在總徑流中的比重[7]，從而對徑流形成過程產生重要影響。

淮河流域位于我國南北氣候過渡帶，氣候變化復雜，降水時空分布不均勻，淮河上游干流及其南部山區的河道坡度大，匯流時間短，極易發生短歷時高強度的山洪[8]。同時，土壤大孔隙和大孔隙流在淮河流域普遍存在[9]，對徑流形成過程產生重要影響。因此，本文以淮河流域上游的黃泥莊小流域為研究區，引入變動滲漏面積方法為HBV模型增添大孔隙模塊，探究改進后的HBV模型在該流域山洪預報中的適用性。

2 研究區域及數據來源

2.1 研究區域

選擇淮河上游黃泥莊水文站以上集水區(下文簡稱黃泥莊流域)為研究區，該研究區介于北緯31°06′～31°38′和東經115°21′～115°43′之間，流域控制面積805 km2。該流域地處我國南北氣候過渡帶，多年平均氣溫為11～16 ℃，流域多年平均年降水量為1 077 mm[10]，但降水的年內分布不均。流域年降水量的50%～80%集中在汛期(6-9月)[10]，且多以暴雨形式出現。汛期降水歷時短、強度大、暴雨中心籠罩范圍小，因此汛期時由暴雨引發的山洪頻發。流域內植被發育良好，森林覆蓋率高達65%，存在豐富的地下水和壤中流。流域平均海拔為479 m，但地形復雜，西北和東南以山地為主，河道坡度大，雙扇形河網使區域產流快速向流域出口匯集。流域概況如圖1所示。

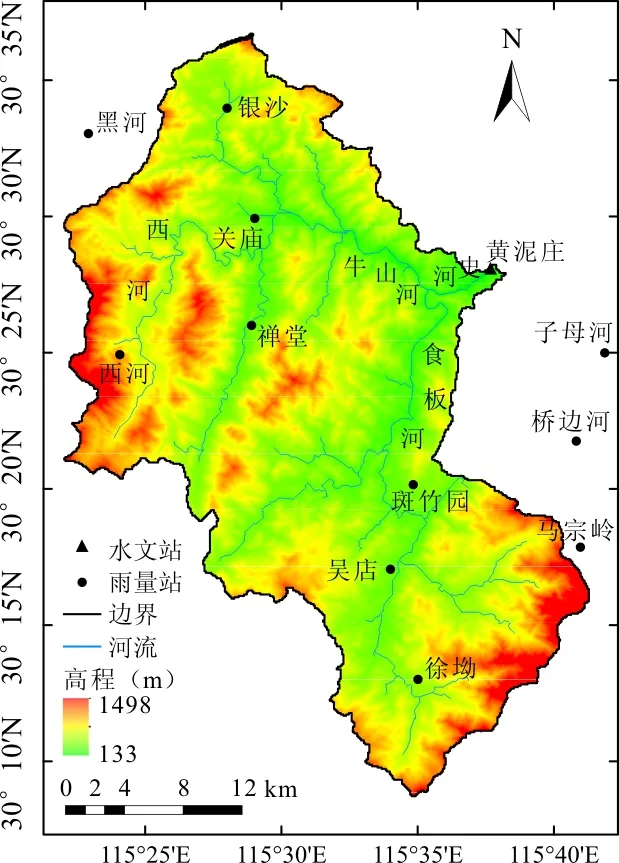
圖1 黃泥莊流域概況

2.2 數據來源

如圖1所示，黃泥莊流域有相對密集的降水觀測站網，流域及其周邊的12個雨量站點的降水觀測數據可以從淮河流域水文年鑒資料中獲取。但是獲取的長歷時資料主要以日尺度觀測為主，僅在必要時進行小時尺度加密觀測。因此，該項研究僅選擇了2010 -2015年間有小時尺度觀測數據的特定洪水事件進行研究。考慮到12個雨量站點在黃泥莊流域分布相對均勻，在對雨量站的降水數據仔細檢查后，使用泰森多邊形面積權重方法獲取小時尺度流域面平均雨量。另外，由于雨量站缺乏氣溫觀測且流域范圍內沒有國家氣象站，因此使用了高分辨率的歐洲中期天氣預報中心再分析產品(ECMWF)的逐小時氣溫數據作為HBV模型的驅動，該產品已經被證明在中國區域有很好的應用效果[11-12]。黃泥莊水文站的徑流觀測資料來自淮河流域水文年鑒洪水要素摘錄表。為了與模型輸出結果進行匹配，研究中使用了線性插值方法對加密觀測的洪水摘錄資料進行插值處理，進而得到洪水事件期間逐小時的流量觀測資料。

考慮到下游的防汛承受能力，研究中以500 m3/s為閾值，在2010-2015年間共選擇了6次洪水事件(詳細信息如表1所示)，且在選定的洪水事件期間，12個雨量站都有完善的加密降水觀測資料。從表1中可以看出，2010-2015年期間每年都至少有1次較大洪水，且洪水事件主要集中在每年的6-7月間。其中，最嚴重的1次發生在2013年，洪峰流量高達1 628.49 m3/s。

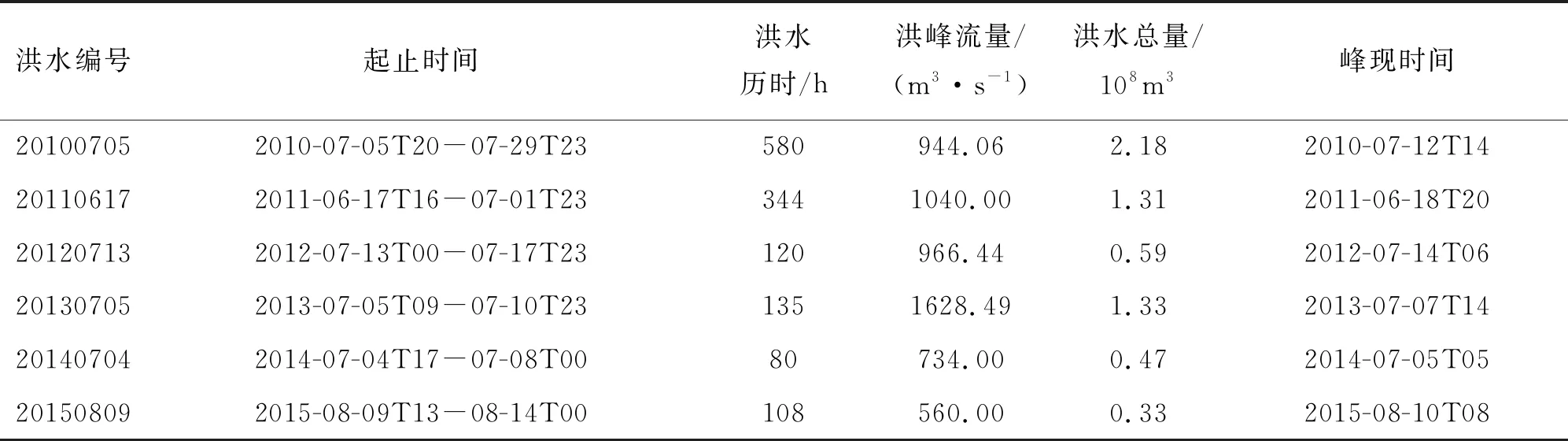
表1 黃泥莊流域2010-2015年洪水事件概況

3 HBV模型改進

3.1 概述

HBV模型為概念性水文模型，它具有輸入參數少、適用性強、模擬精度高等優點，可以適用于各種復雜氣候條件下的水文模擬，目前已被廣泛應用于水文預報、氣候變化研究、水資源評估、地下水模擬和水量平衡研究等方面[13-14]。HBV模型以降水量、氣溫和潛在蒸散發為主要驅動，輸出出口斷面徑流量。如圖2所示，HBV模型主要由3個部分組成，分別是：積雪與融雪模塊、土壤濕度計算模塊和徑流響應模塊。考慮到大孔隙對HBV徑流響應過程的影響，研究中使用變動滲漏面積方法對上層水庫進行改進，詳細描述如下。

圖2 考慮大孔隙的HBV模型結構

3.2 積雪和融雪模塊

HBV模型采用閾值方法進行雨雪分割(此次研究中使用0 ℃為雨雪分割閾值)，且模型假定融雪和積雪速率與溫度成正比。當溫度低于閾值溫度時，降水主要以雪的形式累積為積雪，反之則為降雨。當溫度一直保持在閾值溫度以下時，則不會產生徑流，但溫度一旦超過閾值溫度，融雪徑流開始產生，其中融雪速率如下式：

Sm=DD(T-Tt)

(1)

式中：Sm為融雪速率，mm/h；DD為度日因子，mm/(℃·h)；T為小時平均氣溫，℃；Tt為閾值氣溫，℃。

3.3 土壤濕度計算模塊

流域的降水通常分為兩部分：一部分滲入土壤；另一部分用于形成地表徑流，即為時段徑流深ΔQ。一般來說，土壤含水量越高，降水對徑流形成的貢獻就越大，當土壤含水量接近最大土壤含水量時，下滲量減少，降水對產流量的貢獻增加。時段徑流深的計算如下：

(2)

式中：ΔQ為時段徑流深，mm；SM為實際土壤含水量，mm；FC為最大土壤含水量，mm；β為形狀系數。

由于蒸散發與氣溫息息相關，模型采用氣溫折算方法獲取小時尺度潛在蒸散發。如公式(3)所示，利用小時平均氣溫與日平均氣溫之間的差值來修訂日平均潛在蒸散發，進而獲取小時尺度的潛在蒸散發。考慮到實際蒸散發受土壤含水量影響很大且與修正后的潛在蒸散發呈線性關系，因此當土壤含水量大于或等于土壤凋萎含水量時，實際蒸散發就等于修正后的潛在蒸散發；當土壤含水量小于土壤凋萎含水量時，受限于土壤水分不足，實際蒸散發將使用土壤含水量與凋萎含水量的比例進行折算。

PEa=(1+C(T-Tm))PEm

(3)

(4)

式中：PEa為修正后的潛在蒸散發，mm；Tm為日平均氣溫，℃；PEm為日平均潛在蒸散發，mm；C為模型參數；Ea為實際蒸散發，mm；PWP為土壤凋萎含水量，mm。

3.4 改進后的徑流響應模塊

HBV模型將徑流形成過程概化為一個響應函數，該函數由一個上層非線性水庫和一個下層線性水庫組成，即把徑流成分概化為兩個響應盒子。上層盒子有兩個徑流出口，其響應函數通過消退系數K0、K1來體現，下層盒子有一個徑流出口，其響應函數通過消退系數K2來體現。當上層盒子水位超過閾值L時，上層盒子迅速形成地表徑流(Q0)，并從第一個出口流出。上層盒子的第二個出口和下層盒子出口的徑流響應相對較慢，形成壤中流(Q1)和基流(Q2)。流域出口徑流深(Q)即為各部分徑流深之和。

(5)

(6)

Q=Q0+Q1+Q2

(7)

式中：Su為上層水庫水位，mm；Sl為下層水庫水位，mm；L為閾值水位，mm；K0為地表徑流消退系數；K1為壤中流消退系數；K2為基流消退系數；Q0為地表徑流，mm；Q1為壤中流，mm；Q2為基流，mm；Q為總徑流深，mm。

但是，HBV模型中并未考慮大孔隙對降雨入滲的促進作用以及大孔隙的存在對徑流組成成分的影響，所以模擬出的洪水過程線可能不準確，尤其是對洪峰的模擬精度較差。考慮到這一點，研究中將研究區劃分為設置模擬大孔隙下滲的變動滲漏面積和一般透水面積兩部分，且變動滲漏面積與土壤含水量有關。參考肖慶元等[9]的研究結果，變動滲漏面積和一般透水面積劃分如下：

(8)

式中：AA為變動滲漏面積所占比例；BB為一般透水面積所占比例；IA為AA的上限；n為經驗指數。

在增加大孔隙模塊后，改進的HBV模型中，將上層盒子分為兩個部分：變動滲漏部分和一般透水部分。在變動滲漏部分，下滲能力很強，一般情況下水可以沿著大孔隙直接進入下層盒子而無損失；在一般透水部分，仍然依據HBV模型的滲透常數方法進行，改進后的上層土壤滲流可以表述為：

Qprec=Su·Kprec+AA·ΔQ

(9)

式中：Kperc為滲流消退系數；Qprec為滲流，mm。

3.5 模型評價標準

根據《水文情報預報規范》(SL 250-2000)，采用Nash-Sutcliffe效率系數即Nash系數、洪峰流量相對誤差、洪量相對誤差和峰現時間誤差來衡量模型的模擬效果，它們的計算公式和最優值如表2所示。Nash系數反映的是徑流模擬值與觀測值之間的吻合度，洪峰流量相對誤差反映的是對洪峰的模擬效果，洪量相對誤差反應的是對洪水總量的模擬效果，峰現時間誤差反映的是對洪峰出現時間的模擬效果。

表2 模型評價指標

4 模擬結果和分析

4.1 參數敏感性分析

在改進的HBV模型中，IA表示變動滲漏區在流域中所占的最大比例；n為經驗指數，反映隨著土壤濕度變化，變動滲漏區中實際大孔隙區域的變化。由公式(8)可知，當IA為定值時，隨著n的增加，流域中大孔隙實際所占的面積逐漸減少；反之，當n為定值時，隨著IA的增加，實際大孔隙面積比例增加。當IA=0時，變動滲漏面積所占比例為0，可認為土壤中不存在大孔隙；當IA=1，n=0時，變動滲漏面積所占比例為1，可認為土壤中全是大孔隙。為分析模型改進效果，并確定新增大孔隙模塊主要控制參數的敏感性，不失一般性的選擇20100705次洪水為例，采用控制變量法分析參數IA和n對洪峰流量和洪水總量的影響，即使IA在0.1～1之間以0.1的步長均勻變化，n在0～0.8之間以0.2的步長均勻變化，統計IA和n的變化對洪峰流量和洪水總量的影響，結果如圖3和4所示。

由圖3和4可知，洪峰流量和洪水總量對新增加大孔隙模塊的兩個參數都很敏感。隨著IA的增加和n的減小，流域中大孔隙所占面積逐漸增加，洪峰流量和洪水總量均隨之減小且洪峰流量的變率遠超洪水總量。這主要是由于流域孔隙度的增加促進了土壤的快速入滲進而產生了更多的壤中流，而壤中流的匯流時間較長使得模擬洪水過程線坦化，降低了洪峰的模擬值。深入分析可以發現，IA和n之間有著復雜的相互關聯。當IA較小時，變動滲漏區域在流域中的占比較小，洪峰流量和洪水總量對n的變化響應強度較弱，隨著IA的增加，曲線的分布更加分散，表明此時主要的控制參數為經驗參數n。總的來說，對于IA而言，其高值區間比低值區間更加敏感，而對n而言則是低值區間更加敏感。

4.2 模擬結果分析

基于改進后的HBV模型，對2010-2015年間選定的6次洪水事件進行模擬，其中前4次洪水事件用來校準模型，采用試錯法獲取模型的最優參數[15]，后2次洪水事件用來檢驗模型結果。

表3匯總了6次洪水事件模擬結果的統計指標，總的來說，改進后的HBV模型在黃泥莊流域洪水模擬中模擬效果較好。率定期的4次洪水事件Nash系數分別為0.82、0.92、0.91和0.89；驗證期的兩次洪水事件Nash系數分別為0.92和0.76，能較好地匹配兩個時期洪水過程。除明顯低估了20130705次洪水的洪峰流量外(洪峰流量相對誤差為-28.38 %)，其余洪峰流量和洪量相對誤差均在20 %以下，能較好地捕獲洪峰流量和洪量，對災害預警和災情評估有重要意義。此次率定期和驗證期的峰現時間誤差均在2 h以內，改進后的HBV模型能夠準確地再現洪峰出現時間。依據《水文情報預報規范》(SL 250-2000)，6次洪水事件的模擬精度均達乙級及以上標準，滿足實際工程應用精度，可用于該流域洪水模擬與預報。

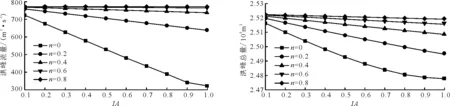
圖3IA-n-洪峰流量相關圖 圖4IA-n-洪水總量相關圖

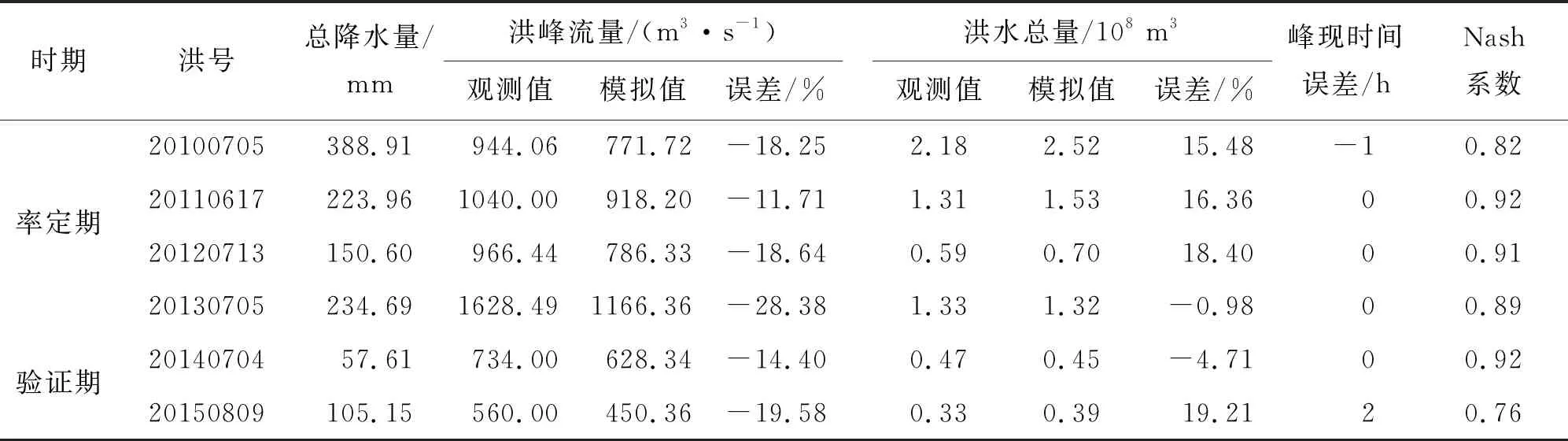
表3 黃泥莊流域洪水模擬結果

圖5和6分別展示了率定期和驗證期洪水過程線的觀測值和改進后HBV模型的模擬結果。如圖1所示，黃泥莊流域由南北兩個扇形子流域構成，洪水漲落迅速，主要以單峰的尖細洪水過程為主(圖5和6)。盡管改進后的HBV模型能較好地模擬洪水過程線，但依然傾向于低估洪峰。這可能是受限于集總式模型結構特征，改進后的HBV模型依然難以刻畫徑流過程對流域降水空間異質性的響應。同時，黃泥莊流域的雨量站點均分布在靠近河道的相對平緩的谷地，對坡面地形雨及短歷時暴雨的捕獲率不足，難以準確反映洪峰對應期流域降水，這也進一步加劇了HBV模型對洪峰流量的低估。另外，可能是受到前期土壤濕度的影響，黃泥莊流域水文過程線對小雨并不敏感，這也導致HBV模型高估了洪水過程的起漲點(例如20100705和20130705洪水)，后續的研究需要針對這一過程進行進一步的改進。集總式HBV因其具有模型結構相對簡單、計算量小、模型參數和所需驅動數據較少等優點，已經被廣泛應用于洪水模擬與預報，但對降雨徑流過程概化不足也進一步增加了模型的不確定性。總體而言，添加對物理過程的精細化描述能進一步提高模型的模擬精度。

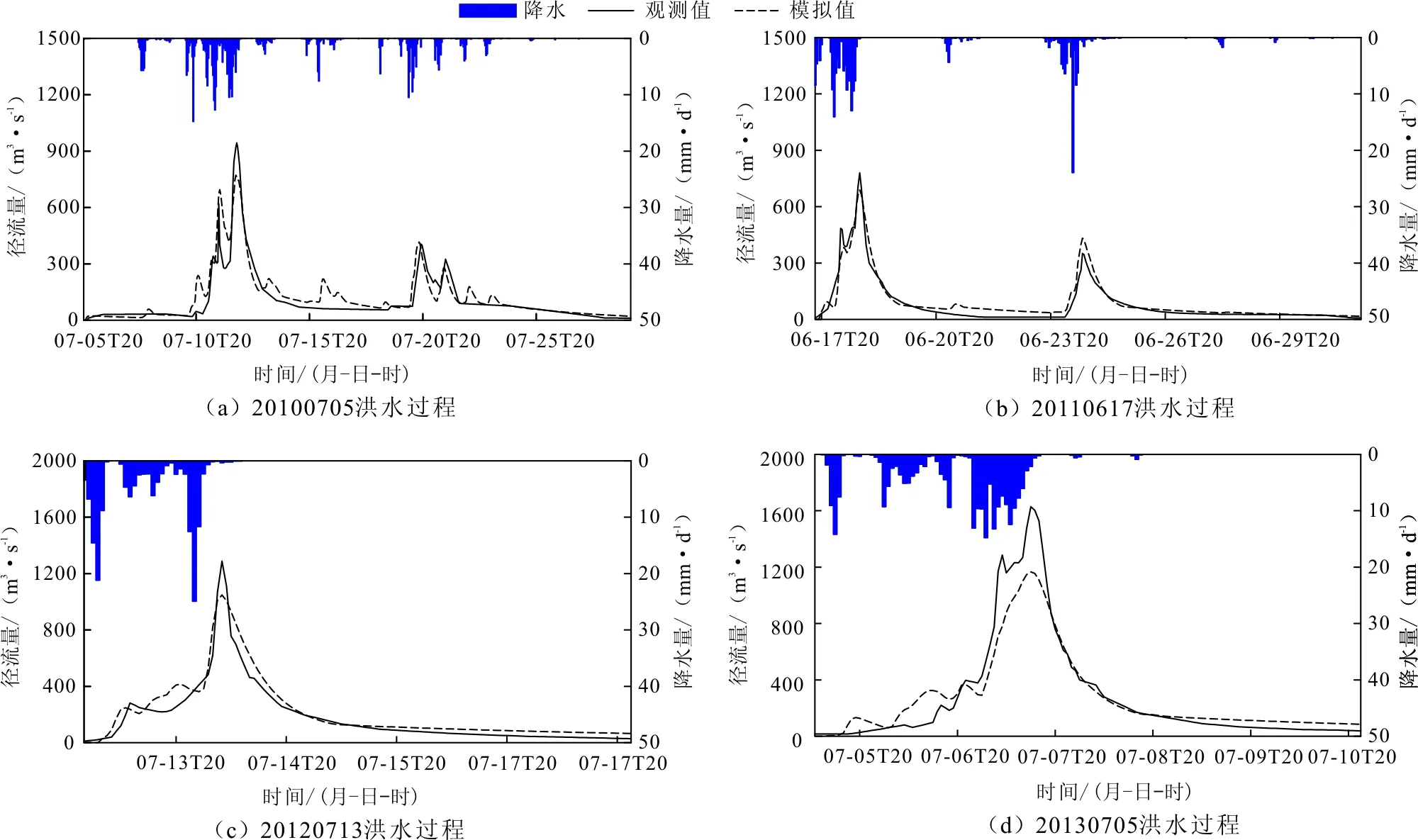
圖5 模型率定期觀測和模擬的洪水過程線

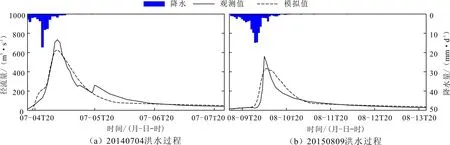
圖6 模型驗證期觀測和模擬的洪水過程線

5 結 論

無資料小流域的山洪預報一直是洪水預報中的一個難點，土壤大孔隙及其引發的大孔隙流通過改變流域產匯流過程，進一步增加了這類地區洪水模擬與預報的難度。本文使用變動滲漏面積法改進HBV模型，并以淮河流域上游黃泥莊小流域為例，對2010- 2015年的6次洪水事件進行模擬，得出了以下結論：

(1)大孔隙模塊的控制參數IA和n的變化會對洪峰流量和洪水總量產生較大影響。

(2)率定期的Nash系數在0.82～0.92之間，驗證期的Nash系數在0.76～0.92之間，洪峰流量相對誤差和洪量相對誤差基本控制在20 %以內，峰現時間誤差不超過2 h。3次洪水事件的模擬精度達到洪水預報甲級標準，3次達到乙級標準，說明改進后的HBV模型能夠很好地模擬黃泥莊流域的洪水過程，滿足該流域的實際應用需求。

(3)本研究可為淮河流域山區的防洪減災、水資源管理調度等提供參考。同時，引入變動面積方法對HBV模型的改進和對存在大孔隙的相似小流域山洪預報研究有重要的借鑒意義。