一種單自由度3T1R并聯機構的拓撲設計及其運動學

沈惠平 呂 蒙 朱小蓉 李云峰

常州大學現代機構學研究中心，常州，213016

0 引言

工業上許多場合需要結構簡單、少驅動源但能產生空間復雜運動的空間機構。在提出、研制單自由度并聯運動振動篩的基礎上［1－3］，筆者提出了“少輸入-多輸出”（Fi－Mo）并聯機構的概念，建立了驅動輸入數、自由度數、動平臺輸出運動個數（含獨立和非獨立元素）三者之間的數學模型［4］，并提出了Fi－Mo機構的兩種設計方法［5］；據此，設計了大量少輸入-多輸出并聯機構［6－8］；進一步，發明并設計了基于單自由度三轉動輸出并聯機構的肩關節康復訓練機［9］、并聯式腳底按摩機［10］以及多種輸出形式的并聯振動篩［11］，為其他新型節能裝備的設計、研發奠定了理論基礎。單自由度的Fi－Mo機構是一種新型并聯機構［4－5］，因其驅動元件少、造價低、結構緊湊，所以有著較高的實用價值和應用前景，但目前對Fi－Mo并聯機構的運動學、動力學研究還較少。

本文提出了一種新型的單自由度三平移一轉動（3T1R）并聯機構，分析了該機構的方位特征（position orientation characteristic，POC）、自由度（DOF）及耦合度κ等拓撲特性，導出了其運動位置正逆解、速度與加速度公式，此外為該機構用于產生3T1R的振動篩分裝置進行了3D虛擬樣機設計。

1 機構設計

本文提出的單自由度3T1RFi－Mo并聯機構如圖1所示，它由靜平臺0、動平臺1以及連接兩平臺 之間的 一條混 合支鏈（hybrid single－openchain，HSOC）HSOC1和一條簡單支鏈組成，其中，混合支鏈由支鏈Ⅰ（即 R11‖R12－P（4R））和支鏈Ⅱ（即 R21－P（4R）-R22）并聯連接后，與轉動副 R13串聯而 成，可 表 示 為 R11‖R12－P（4R）‖R22－P（4R）－R21）-R13，其中，P（4R）表示由4個 R 副組成的平行四邊形等效產生的一個P副，其末端構件（動平臺1的一部分）輸出為三平移一轉動；而簡單支鏈Ⅲ為 R31－S32支鏈。

靜平臺0上轉動副R11、R21的軸線和動平臺1上的R13軸線平行；轉動副R31的軸線平行于R11R21的連線。

2 機構的拓撲分析

2.1 機構POC集分析

（1）串聯、并聯機構的POC集方程［12］分別為

式中，MJi為第i個運動副的POC集；Mbi為第i條支鏈末端的POC集；MPa為機構動平臺的POC集。

（2）選取動平臺上1的任意一點為基點p。

（3）確定支鏈末端構件的POC集。由第1節可知，混合支鏈HSOC1是由支鏈Ⅰ、支鏈Ⅱ并聯后，與轉動副R13串聯而成，由式（1），它們產生的POC集分別為

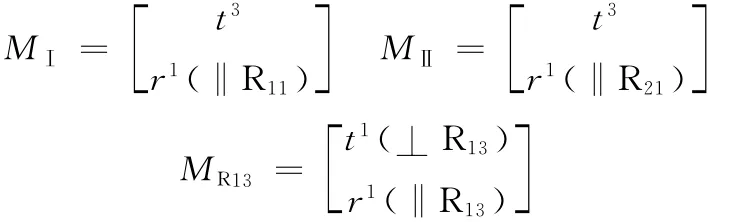
由式（1）、式（2），有

（4）確定動平臺的POC集。由式（2），得則動平臺1可產生3個平移及1個繞轉動副R13軸線的轉動。

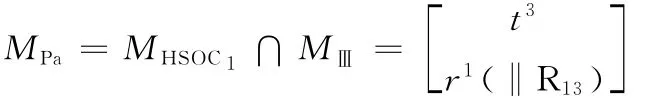
2.2 自由度計算

（1）并聯機構的全周自由度公式［12］為

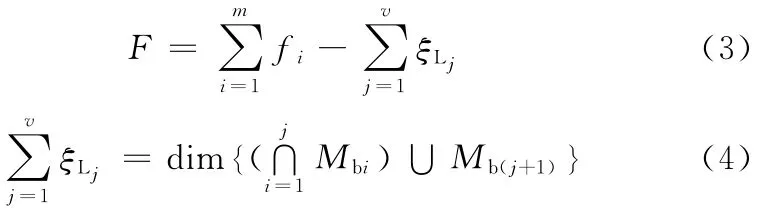
式中，F 為機構自由度；fi為第i個運動副的自由度；m為運動副數；v為獨立回路數（v＝m－n＋1，n為構件數）；ξLj為第j個獨立回路的獨立位移方程數；dim為POC集的維數為前j條支鏈組成的子并聯機構POC集；Mb（j＋1）為j＋1條支鏈末端構件的POC集。

（2）確定各回路的獨立位移方程數。此機構可分解為兩個獨立回路，即單開鏈（single open chain，SOC）SOC1｛R11‖R12－P（4R）‖R22－P（4R）‖R21｝和SOC2｛R31－S32－R13｝。其獨立位移方程數計算方法如下：

①支鏈Ⅰ、Ⅱ組成第1個獨立回路，由式（4）可得

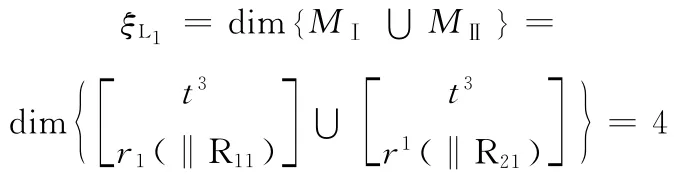
由式（2），該子并聯機構的POC集為

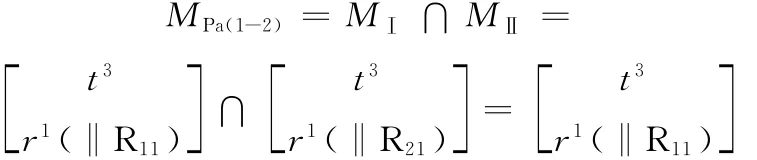
由式（3），該子并聯機構的自由度為

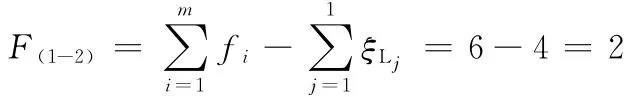
則子并聯機構的輸出僅有2個獨立運動。

②上述子并聯機構、R13及單開鏈SOC2組成第2個回路，由式（4）可得

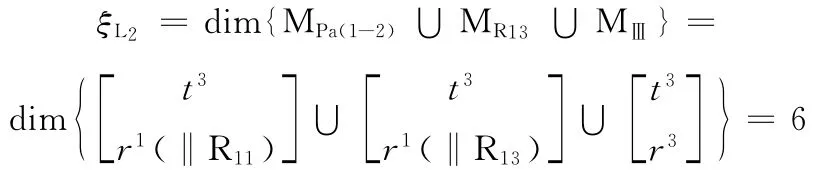
（3）確定該并聯機構的自由度。由式（3），得

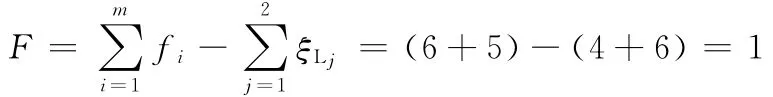
當轉動副R11為驅動時，動平臺1產生3個平移及1個繞轉動副R13軸線的轉動，但其中僅有1個獨立運動，其余3個運動為寄生運動。注：自由度計算時，如將該機構視為僅包含前述的產生3T1R的混合支鏈HSOC1和簡單支鏈Ⅲ組成的一個獨立回路，即混合支鏈等效于）支鏈。顯然，該回路的獨立位移方程數ξ＝6。由式（3）得

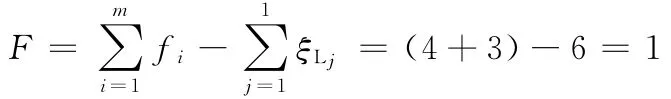
顯然，自由度計算時，采用等效支鏈替代部分復雜支鏈自由度計算較為簡單。

2.3 機構耦合度計算

（1）由基于單開鏈SOC的機構組成原理［12］知，任一機構可分解為一系列單開鏈，而第j個單開鏈SOCj的約束度為

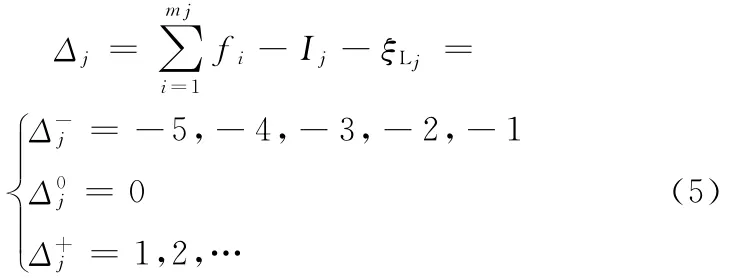
式中，mj為第j個單開鏈SOCj的運動副數；fi為第i個運動副的自由度（不含局部自由度）；Ij為第j個單開鏈SOCj的驅動副數。

進一步，一組有序的v個SOC可構成一個獨立回路數為v的基本運動鏈 （basic kinematics chain，BKC），對一個BKC而言，須滿足

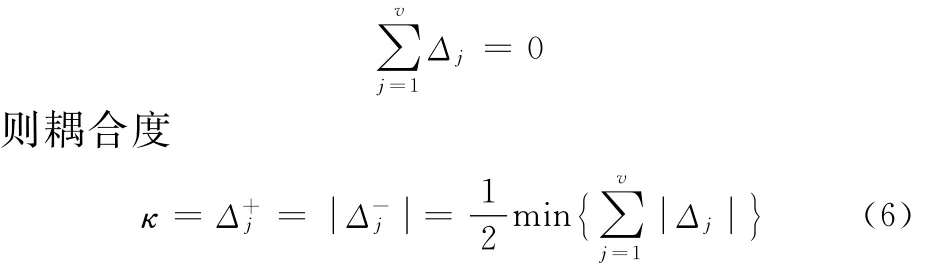
（2）2.2節中已求得兩個回路的獨立位移方程：ξL1＝4，ξL2＝6，則由式（5），得SOC1、SOC2的約束度分別為

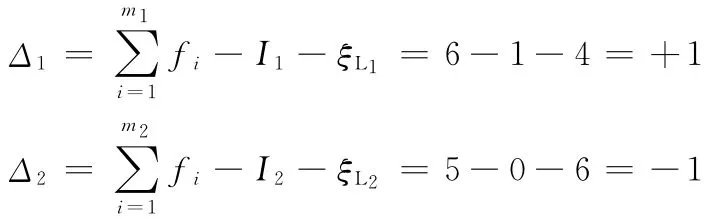
于是，耦合度

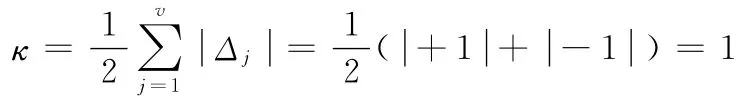
該并聯機構僅包含一個基本運動鏈，其耦合度為1，可用基于序單開鏈法的一維搜索法來求解該機構位置正解。

3 運動學分析

3.1 建立坐標系

如圖1所示，該機構靜平臺0是由轉動副R11、R21、R31為頂點的等邊三角形。動平臺1上的轉動副R13、球副S32分別位于構件1的兩端點。在靜平臺0的幾何中心處o建立固定坐標系oxyz，x軸垂直于R11R31連線且過R21，y軸平行于R11R31的連線，z軸由右手笛卡兒坐標系法則確定；在動平臺1的中點p建立坐標系puvw，v軸為R13S32連線，u軸垂直于v軸，w軸由右手笛卡兒坐標系法則確定，其運動學模型如圖2所示。

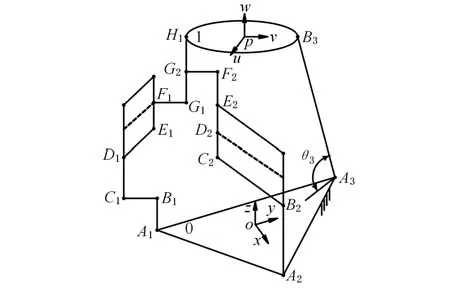
圖2 單自由度3T1R機構的位置計算簡圖Fig.2 Position calculation sketch of 1-DOF 3T1RPM

該機構的結構參數如下：lA1A2＝lA2A3＝lA1A3＝l1，lH1B3＝l2；其余桿長分別為lA1B1＝lC1D1＝0.5l3；lA2B2＝l3；lD1E1＝lB2C2＝l4；lE1F1＝lC2D2＝0.5l5；而lG1G2＝l5；lG2H1＝l6；lA3B3＝l7；lB1C1＝r1、lF1G1＝r2、lF2G2＝r3（為簡化計算，長度為ri的桿長都與靜平臺平行，桿F1G1和桿F2G2都和各自的平行四邊形共面）。

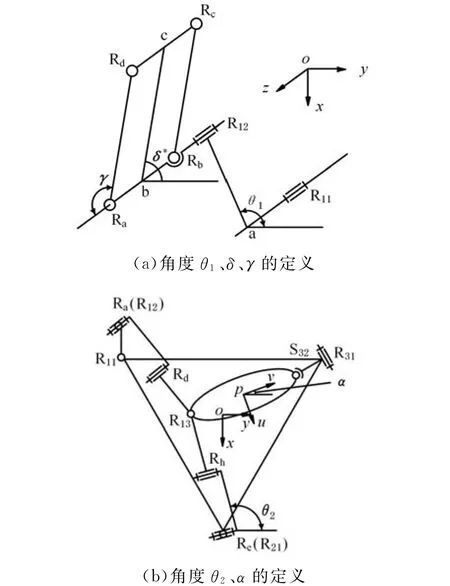
圖3 各角度的定義Fig.3 Definition of angles

各角度定義如下（圖2、圖3）：B1C1與y軸正向的夾角為輸入角θ1，F2G2與y軸正向的夾角為θ2；A3B3與靜平臺的夾角為θ3；D1E1在靜平臺上的投影與y軸正向的夾角為虛擬輸入角δ＊；D1E1與z軸正向的夾角為γ。動平臺p的坐標為（x，y，z），v軸與x軸正向的轉角為動平臺姿態角α。

3.2 基于序單開鏈的機構位置正解求解原理

因機構包含的任一BKC可分解為約束度為正值、零、負值3種形式的單開鏈，因此，機構位置正解的求解可轉化為3種單開鏈的位置求解，而3種單開鏈的約束特性及其建模方法如下。

（1）約束度為正值的SOC（Δ＋i）會使機構自由度增加Δ＋i；為確定其運動，需在約束度為正值的SOC（Δ＋i）上設定Δ＋i個虛擬變量（Δ＋i＝κ）。

（2）約束度為零的SOCΔ0i（）不影響機構自由度，其運動具有確定性，即其位置正解能獨立求解。

（3）約束度為負值的SOC（Δi－）使機構自由度減少 Δi－，即對機構施加了 Δi－個約束方程（Δi－＝κ）。

因SOC（Δi＋）中的虛擬變量數目Δi＋恰等于約束方程數目 Δi－，易建立含Δi＋個變量的位置方程；之后可得到含一個變量的高次方程并求得其封閉解，或用一維搜索法直接求得數值解。

3.3 位置正解分析

位置正解問題歸納為：已知1個驅動輸入θ1，確定動平臺的位置p （x，y，z）和姿態角α。

3.3.1 在約束度Δ1＝1的單開鏈SOC1上

在支鏈Ⅰ、Ⅱ上，分別求得G2點的坐標為

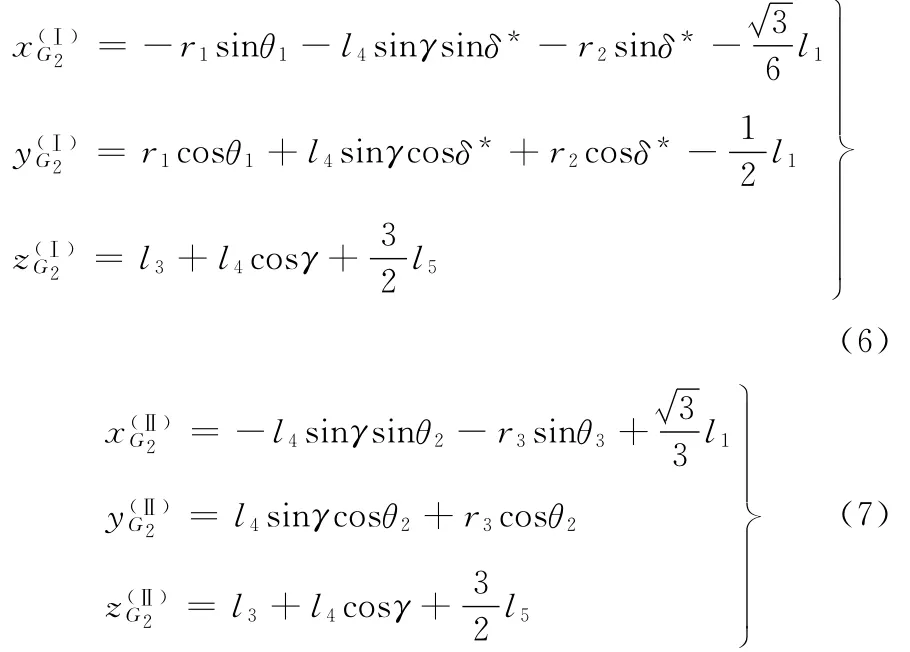
由式（6）、式（7）可得

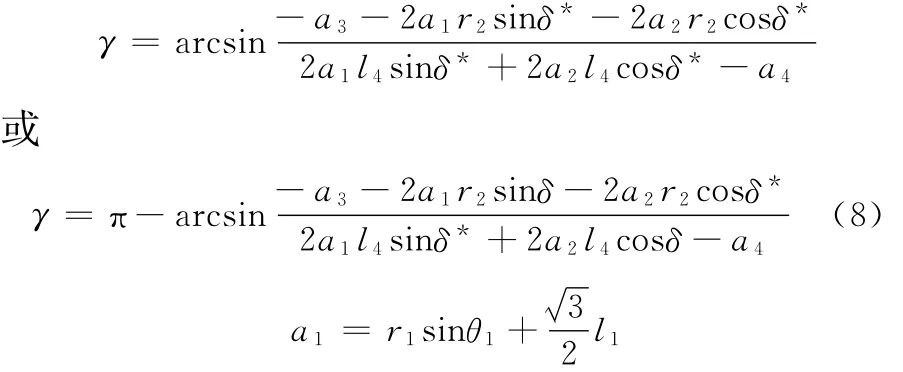
由式（8）可知，γ為虛擬輸入角δ的函數。

3.3.2 在約束度Δ2＝－1的單開鏈SOC2上

由支鏈Ⅰ、Ⅲ，分別求得p點的坐標為

由式（11）、式（12）易知，θ3、α 也為虛擬輸入角δ的函數。進一步，由，得

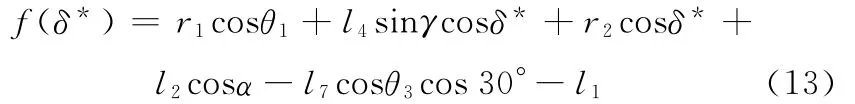
將式（8）、式（11）、式（12）代入式（13），可得到只含有虛擬變量δ＊的方程；通過不斷改變δ＊的值，找到滿足f（δ＊）＝0的真實δ＊所有解。最后，將真實的δ＊代入式（10）、式（12），可得到動平臺位置p（x，y，z）和姿態角α。

3.4 位置逆解分析

機構反解問題為：已知動平臺的位置p（x，y，z）及姿態角α，求驅動副的輸入角θ1。由位置正解式（9），可得到

3.5 速度分析

機構速度問題可描述為：已知驅動副R11的轉速θ·1，求動平臺的質心p的線速度v及角速度α。分別令式（6）、式（7）相等以及式（9）、式（10）相等，并對時間求導，消元化簡可得

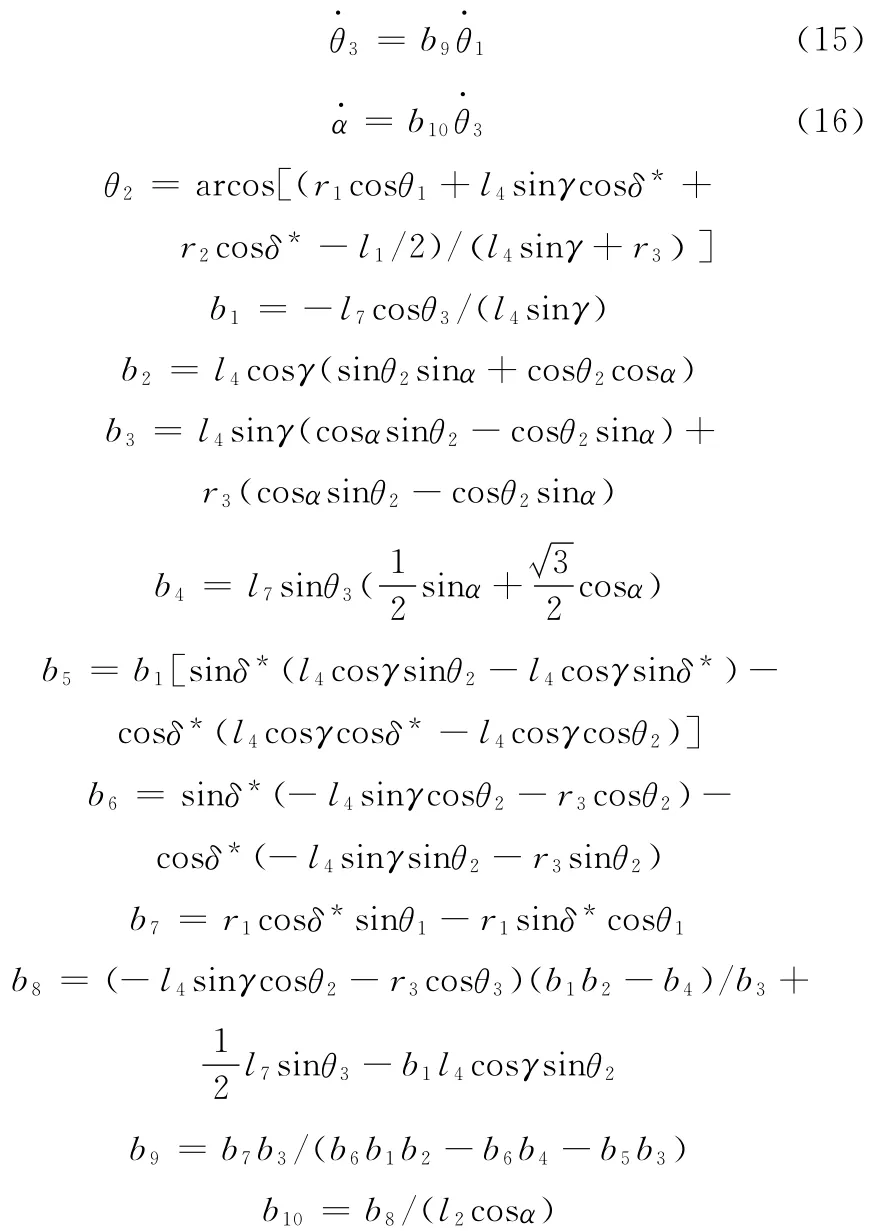
對式（10）求導，可得

由式（16）、式（17）即可得到動平臺的質心速度及其角速度。

3.6 加速度分析

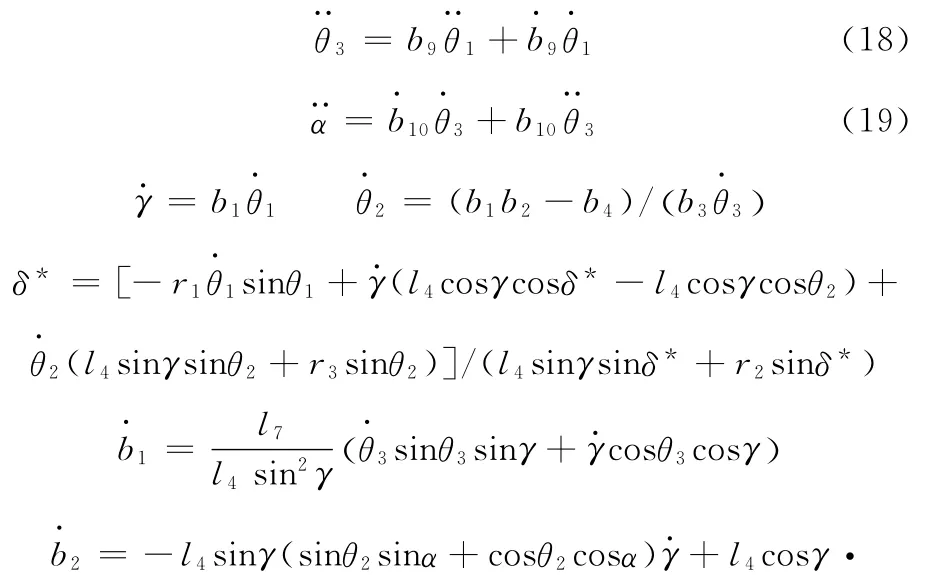
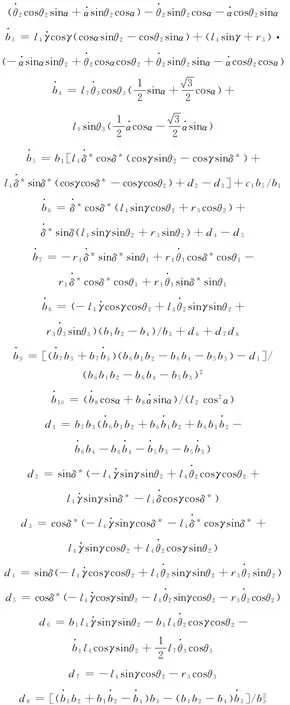
對式（17）求導可得

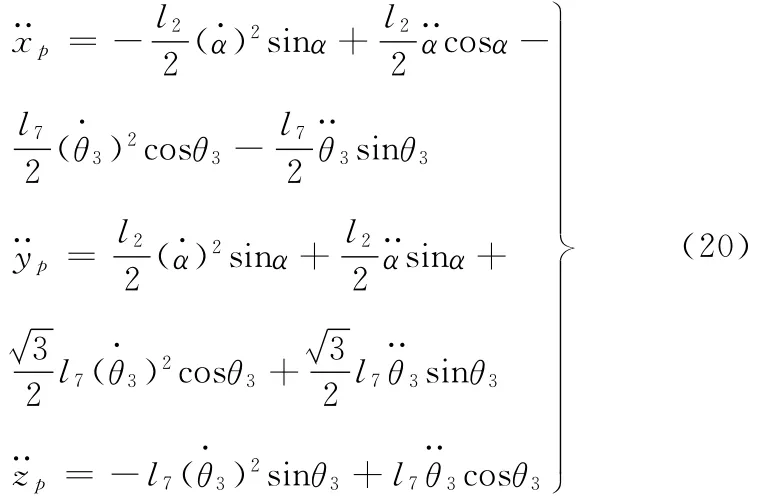
由式（19）、式（20）即可得到動平臺的質心加速度及角加速度。

4 計算實例

4.1 位置正反解算例

設該并聯機構的結構參數如下：l1＝250 mm；l2＝88mm；l3＝81.75mm；l4＝120mm；l5＝24mm；l6＝17mm；l7＝180mm；r1＝29.75 mm；r2＝30mm；r3＝45mm；設輸入角θ1＝30°，由一維搜索法可得兩組實數正解，見表1，對應的裝配構型如圖4、圖5所示。

表1 位置正解數值Tab.1 Numerical values of direct kinematics

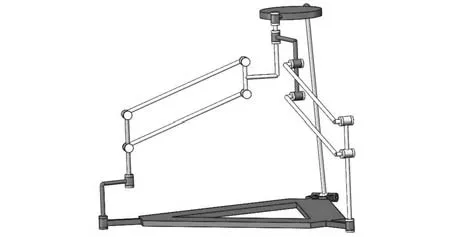
圖4 位置1對應的裝配構型Fig.4 Assembly configuration of Position1

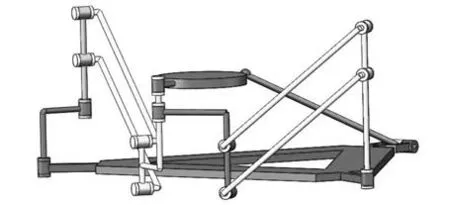
圖5 位置2對應的裝配構型Fig.5 Assembly configuration of Position2

將正解1數據代入式（13），得其中一組解為θ1＝29.998 2°，從而驗證了正反解的正確性。

4.2 速度和加速度算例

用ADAMS進行運動仿真，也可得到該機構動平臺p的速度與加速度曲線，見圖6、圖7所示。

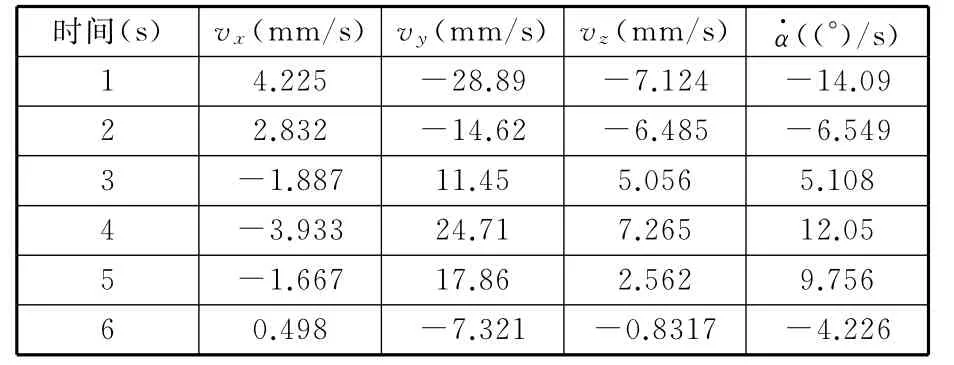
表2 動平臺的速度分析Tab.2 Velocity of moving platform

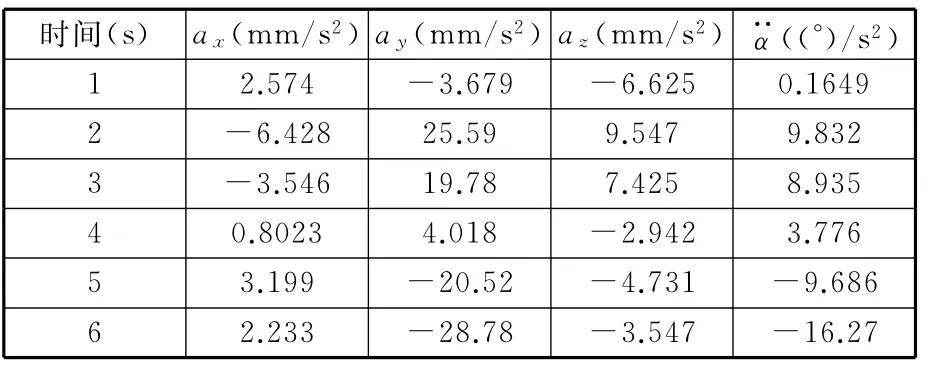
表3 動平臺的加速度分析Tab.3 Acceleration of moving platform

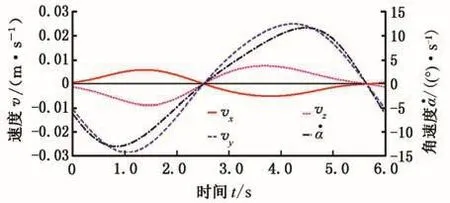
圖6 動平臺的速度曲線Fig.6 Velocity curve of moving platform

由表3知：由加速度公式（20）得到的數值（t＝2s時，ax＝ －6.428mm／s2；ay＝25.59 mm／s2；az＝9.547mm／s2；α··＝9.832（°）／s2），與加速度仿真曲線（圖7）得到的數值（t＝2s；ax＝－6.5mm／s2；ay＝25.7mm／s2；az＝9.7mm／s2；α··＝9.633 7（°）／s2）基本一致，故速度、加速度導出公式正確。

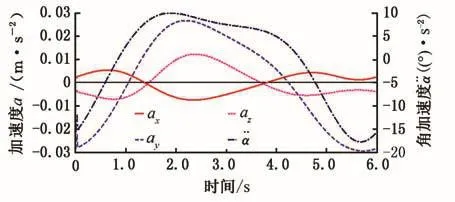
圖7 動平臺對應的加速度曲線Fig.7 Acceleration curve of moving platform

5 并聯振動篩的虛擬樣機

單自由度3T1R并聯振動篩的樣機設計如圖8所示，它包含靜平臺0、動平臺1、由支鏈Ⅰ和支鏈Ⅱ組成的混合支鏈、RS型支鏈Ⅲ以及驅動系統5大部分，可用SolidWorks分別建立其CAD設計模型。

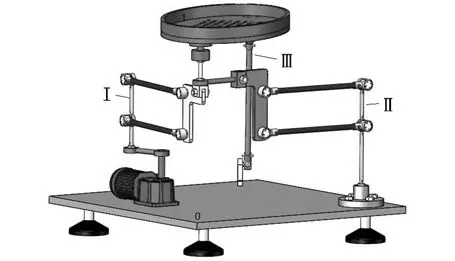
圖8 單自由度3T1R并聯振動篩虛擬樣機Fig.8 Virtual prototype of 1-DOF 3T1R parallel vibrating screen

為了保證振動篩有足夠的剛度和強度，支鏈Ⅰ、Ⅱ的平行四邊形及支鏈Ⅲ采用密度小、強度高、易加工的鋁合金；同時，在與轉動副R22連接的短邊2處宜采用鋁板，從而保證它能傳遞一定的轉矩而不變形，如圖9所示。篩分裝置的靜平臺為長方形鋼板，橢圓形篩箱為動平臺，其長半徑方向為篩分物料的給料方向。

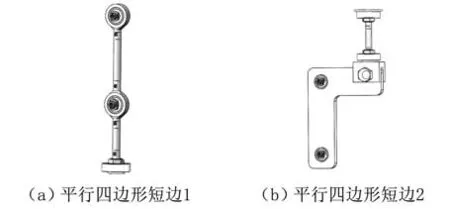
圖9 并聯機構支鏈結構設計Fig.9 Design of the limbs

6 結論

（1）提出了一種低耦合度（κ＝1）的單自由度3T1R并聯機構，該機構結構簡單、驅動源少，可用于振動篩分機構。

（2）根據序單開鏈法的運動學建模原理，建立了一個含1個變量的機構位置正解求解方程，并運用一維搜索法得到了該機構的位置正解。

（3）根據導出的正解公式，導出了該機構的速度與加速度公式，并運用ADAMS軟件仿真驗證了機構的速度與加速度曲線。

（4）給出了基于該單自由度并聯機構的3T1R維并聯振動篩的虛擬樣機設計。

本文工作為該3T1R并聯振動篩的優化、機械結構設計及制造、動力學分析提供了一定的參考。