基于PCA_LDA和協同表示分類的人臉識別算法

聶棟棟，賀悅悅，馬勤勇

(1.燕山大學 理學院，河北 秦皇島 066004；2.燕山大學 信息科學與工程學院，河北 秦皇島 066004)

0 引言

人臉識別是生物識別的一個重要課題，它在身份認證、商業交易、安全保障等多個領域廣泛應用。用計算機對人臉進行識別的過程，大致可分為圖像獲取、特征提取、分類器選擇三大步驟。圖像獲取階段主要是收集圖像數據，通常可以利用一些規范的人臉數據庫。特征提取階段常用的算法有幾何特征的方法[1]，彈性圖匹配模型[2]，子空間算法，如主成分分析(Principal Components Analysis,PCA)、線性鑒別分析(Linear Discriminate Analysis,LDA)、獨立主元分析[3]、小波變換[4]等。在分類階段，常用的分類器有卷積神經網絡[5]、支持向量機[6]、最近鄰分類[7]、基于稀疏表示的分類(Sparse Representation-based Classification,SRC)[8]算法等。

本文提出一種基于PCA主成分分析和LDA線性判別分析，通過協同表示分類(Collaborative Representation-based Classification,CRC)進行人臉識別的算法。首先采用PCA和LDA相結合的方法對人臉數據庫中的樣本信息進行降維和特征提取，然后采用CRC協同表示方法進行分類。該算法克服了主成分分析忽略了數據的類別信息及線性判別分析類內散度矩陣奇異的缺陷，在圖像維數較小的情況下就能夠取得良好的識別效果，而且算法采用協同表示分類，使它具有比經典的基于稀疏表示的分類算法具有更快的處理速度和更好的抗干擾性能。實驗結果也證實，本文算法能夠在不同的姿態、光照和面部表情的變化下，尤其是在強烈的高斯噪聲干擾下達到更好的人臉識別效果，具有非常好的實用價值。

1 PCA_LDA_CRC算法

本文提出的人臉識別算法，在特征提取并降維階段采用PCA和LDA結合的方法，在分類階段采用了CRC協同表示分類方法，因此為了描述方便簡稱其為PCA_LDA_CRC算法。

1.1 PCA_LDA特征提取方法1.1.1 PCA主成分分析法

主成分分析法是模式識別中常用的一種基于統計的特征提取方法，它通過僅損失一些次要信息達到用更低維的特征向量來表示原本的高維信息的目的。

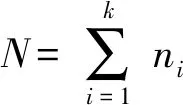
(1)

(2)

在人臉識別中,m被稱做平均臉。通過求解協方差矩陣St的特征值和特征向量，可得到一組由特征向量組成的正交基，稱為特征臉。樣本中任意的人臉圖像都可以用這一組基向量線性表示。將協方差矩陣的特征值從大到小排列：λ1≥λ2≥…≥λd≥λd+1≥…，選取前d個特征值對應的特征向量，構成維數為p×d的主成分變換矩陣P。若前d個主成分的累計貢獻率較高 (80%～99%)時，就可以在不會損失原圖像中太多的特征信息的同時減小人臉特征向量維數。任何一幅人臉圖像向變換矩陣P作投影：y=PTaij，即可獲得d×1的低維向量y，其中系數表示的是圖像在主成分子空間的位置。

PCA人臉識別方法是統計最優的，它使得原圖像與投影圖像之間的均方誤差最小。但是PCA方法同時也存在缺陷。首先它基于圖像像素值的統計，外在因素帶來的圖像差異和人臉本身帶來的差異是無法區分的。因此外界因素，如光照變化、遮擋、噪聲等都會導致識別率降低。而且由于PCA算法側重于準確保留原始圖像特征，而沒有有效利用不同類別之間的差異信息，所以用PCA算法得到的特征是最有表現力的特征，但并不是最有辨別力的特征。

1.1.2LDA線性判別分析

線性判別分析的核心思想是通過求解Fisher判別函數的極值，求得最佳投影向量，將高維空間內的信息投影到更具有分辨能力的低維特征子空間上，并使低維信息達到最小的類內散度和最大的類間散度，即在這個子空間中，各類樣本有最佳的可分離性。

令mi為樣本集中各類樣本的均值：

(3)

則人臉樣本圖像樣本集A的類內散度矩陣Sw和類間散度矩陣SB為

(4)

當類內散度矩陣Sw非奇異時，要想達到最小的類內散度和最大的類間散度，可以求解使類間散度與類內散度比值最大的投影矩陣，即通過如下優化問題求解最佳的投影矩陣L：

(5)

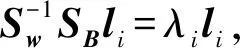
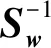
1.1.3PCA_LDA特征提取方法

為了解決上述問題，本文先用PCA對數據進行降維，再用LDA對降維后的數據提取特征，進行二次降維。這樣，不僅充分考慮到數據的類別信息，而且克服了LDA對數據要求嚴格的缺陷。

PCA_LDA特征提取的計算過程如下：

Step 1：由式(1)、(3)分別計算每類樣本和所有樣本的平均值mi,m；

Step 2：根據式(2)計算協方差矩陣St的特征值及特征向量。選擇前d個較大的特征值對應的特征向量，歸一化后組成PCA投影矩陣P；

Step 3：根據式(4)計算樣本集的類內散度矩陣Sw和類間散度矩陣SB；

Step 4：將Sw和SB投影到矩陣P上，并根據目標函數式(5)計算LDA投影矩陣L；

Step 5：計算PCA_LDA特征提取的總投影矩陣W=P×L.

1.2 CRC協同表示分類

自壓縮感知[9]被提出后，就引起了廣泛關注，并成功應用于圖像處理、模式識別[10]等各方面，如Wright等人[8]利用l1范數最小化求出最稀疏的解進行人臉識別。但是l1范數最小化計算復雜，而且目前人們也就SRC方法成功應用于人臉識別是否就是l1范數的稀疏特性所決定的問題，也一直存在著諸多疑問[11-12]。針對以上問題，本文采用一種l2范數最小化的方法，即協同表示方法進行分類。 協同表示的本質就是利用所有類別中的訓練樣本來共同表示待識別樣本。與稀疏表示的算法相比，協同表示的方法大大減小了計算的復雜度，同時增強的算法抗干擾的能力。

在人臉數據庫A的每個類中選取訓練樣本和測試樣本，假設第i類中選取r個作為訓練樣本，剩余的ni-r個做為測試樣本。計算每個訓練樣本aij在PCA_LDA特征提取總投影矩陣W上的投影：

Dij=WT(aij-m),

(6)

將Dij按列組成字典矩陣D，則D∈Rt×q，其中q=k×r表示訓練樣本數目,t表示PCA_LDA提取的特征維數，t≤k-1。

假設任何一個測試樣本y都可以用字典D中的訓練樣本線性表示，即y=Dα，其中α=(a1,a2,…,aq)表示系數向量。協同表示方法是通過l2范數最小化求得系數α：

α=arg min‖α‖2s.t. ‖y-Da‖2<ε，

(7)

引入拉格朗日常數λ，則上式可化為

故α=(DTD+λI)-1DTy。

記VT=(DTD+λI)-1DT，則V表示從測試樣本向量y到表示系數向量α的投影矩陣。而且矩陣V是獨立于測試樣本y的，因此當字典D確定后，可以先計算出矩陣VT，然后對每個測試圖像y，只需計算α=VTy即可。

最后，測試樣本y所在的類為

(8)

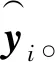
1.3 PCA_LDA_CRC算法過程

假設輸入樣本集A，類別數k，測試樣本y，則利用本文算法對測試樣本進行分類的具體過程如下：

1) 計算PCA_LDA投影矩陣W；

2) 根據式(6)計算訓練樣本y在W上的投影；

3) 計算矩陣VT=(DTD+λI)-1DT；

4) 計算系數向量α=VTy；

5) 根據式(8)得出y的分類f(y)。

1.4 算法的計算復雜度分析

在PCA分析階段，最耗時的處理是對大小為p×p的協方差矩陣St求d個最大的特征值，其復雜度為O(p2d)；在LDA分析階段，將SB和Sw投影到大小為p×d投影矩陣P上后，大小都為d×d，該階段最耗時的處理是求逆矩陣和求特征值，其復雜度是O(d3)；在CRC分類階段，最耗時的是求(DTD+λI)-1，因此該階段的復雜度是O(q3)。上述過程對所有測試樣本只需要計算一次，因此假設總測試樣本數目為s，則復雜度為O((p2d+d3+q3)/s)。又因為p?d，p?q且d,q,s量級相當，故本文算法的復雜度可簡化表示為O(p2)。

2 實驗結果

為驗證算法的有效性，實驗分別在ORL庫[13]和YALE庫、部分FERET庫上進行，其中ORL人臉庫包括40個人的400張圖片；YALE庫包含15個人的165張人臉圖片，每個人11張不同表情與光照條件；FERET庫包含1 400張圖，每人7張，本文選擇其中的40個人作為代表，分別進行實驗。這些實驗數據庫的人臉圖像在光照條件、面部表情等方面存在較大差別，因此這些數據庫不僅可以驗證算法的有效性，而且可以驗證算法的魯棒性。

首先，實驗對本文算法PCA_LDA_CRC與其它幾種典型相關算法的識別率進行了比較，結果見表1～3。其中PCA_LDA_SRC與PCA_LDA神經網絡與本文PCA_LDA_CRC采用相同的特征提取算法，但在分類時分別采用SRC、神經網絡、CRC進行分類。而2DPCA_CRC算法則采用與本文算法不同的2DPCA降維，相同的CRC分類。CRC算法則直接采用下采樣降維后進行CRC分類。表中r表示從每類人臉圖像中隨機抽取的作為訓練樣本的個數。由于樣本抽取的隨機性，所以表中結果是10次測試的平均值。實驗中所有CRC算法中的拉格朗日參數λ為取經驗值0.2。這是根據對參數在0.1到1之間，每隔0.1進行一次實驗，最終各個人臉數據庫下的綜合表現取最好的。

表1 ORL人臉庫上的實驗結果
Tab.1 Test results on ORL face database%

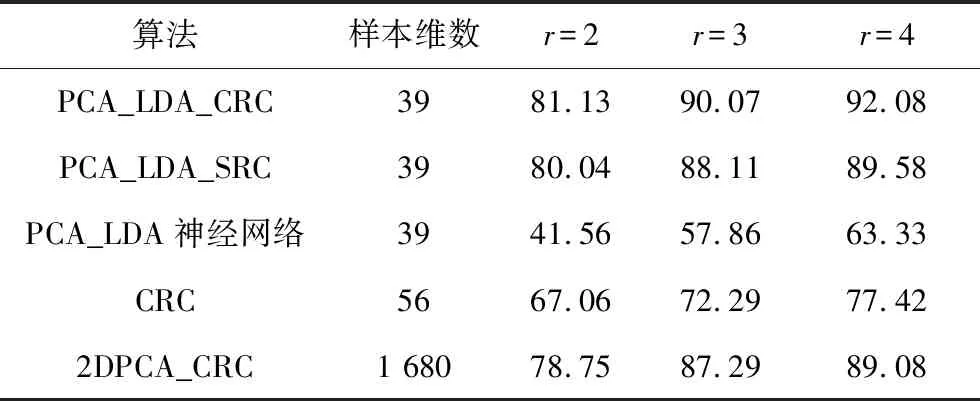
算法樣本維數r=2r=3r=4PCA_LDA_CRC3981.13 90.07 92.08PCA_LDA_SRC3980.0488.1189.58PCA_LDA神經網絡3941.5657.8663.33CRC5667.0672.29 77.42 2DPCA_CRC1 68078.7587.29 89.08

表2 YALE人臉庫上的實驗結果
Tab.2 Test results on YALE face database%

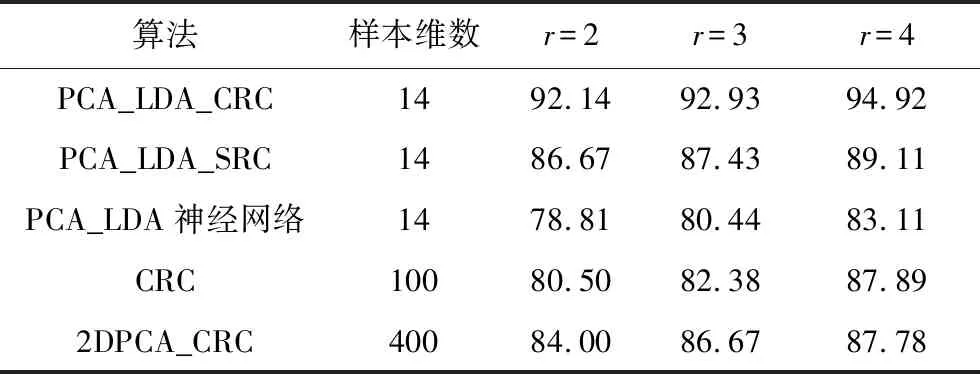
算法樣本維數r=2r=3r=4PCA_LDA_CRC1492.1492.9394.92PCA_LDA_SRC1486.6787.4389.11PCA_LDA神經網絡1478.8180.4483.11CRC10080.50 82.38 87.89 2DPCA_CRC40084.00 86.67 87.78

表3 FERET人臉庫上的實驗結果
Tab.3 Test results on FERET face database%

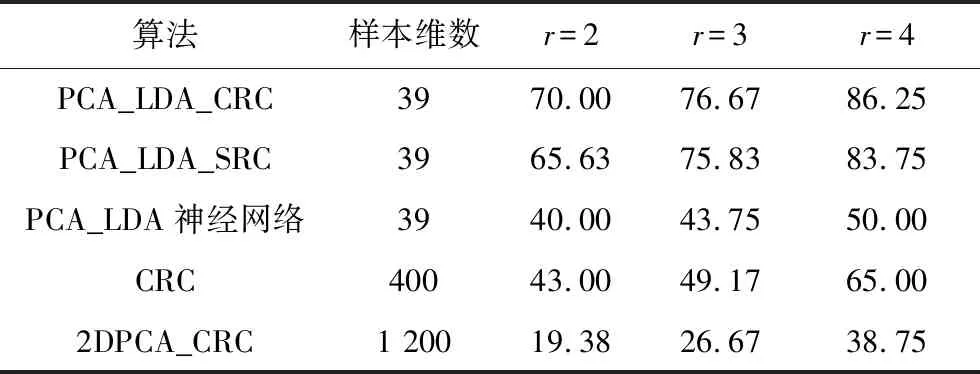
算法樣本維數r=2r=3r=4PCA_LDA_CRC3970.0076.6786.25PCA_LDA_SRC3965.6375.8383.75PCA_LDA神經網絡3940.0043.7550.00CRC40043.0049.1765.002DPCA_CRC1 20019.3826.6738.75

從表1～3結果可以得出以下結論：

1) 本文提出的PCA_LDA_CRC在使用較少的樣本維數的條件下，獲得了比其它幾種相關算法更好識別率。

2) 在ORL、YALE和FERET人臉庫上，本文PCA_LDA_CRC算法的識別效果較為穩定。而CRC和2DPCA_CRC在FERET人臉庫的識別效果都明顯比其它兩種數據庫上的識別效果差很多。PCA_LDA_神經網絡只在YALE人臉庫上稍好，在其它兩個數據庫上識別效果都較差。這證實本文算法能夠更好地消除光照、面部表情等方面的影響，算法具有良好的穩定性。

其次，為了定量分析算法的時間復雜性，本文對上述各算法的處理時間進行了統計。以ORL人臉數據庫為例，每類人臉圖像的訓練樣本數分別是r=2、3、4、5時，平均完成1幅人臉圖像識別的時間，見表4所示。算法采用MATLAB 7.0編寫，表中統計的處理時間是在臺式PC(Intel Core i5-2320 CPU@3.00 GHz，16 GB內存)上運行10次后的平均值。

表4 ORL人臉庫上的處理時間
Tab.4 Processing times on ORL face databasems

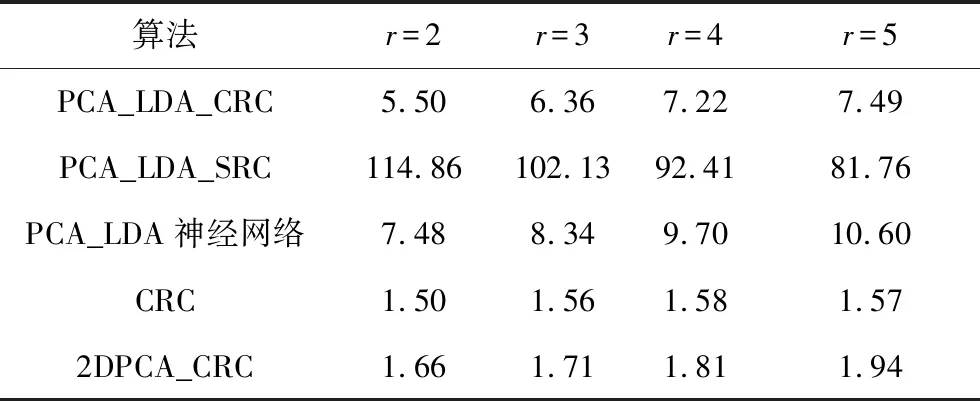
算法r=2r=3r=4r=5PCA_LDA_CRC5.50 6.36 7.22 7.49 PCA_LDA_SRC114.86 102.13 92.41 81.76 PCA_LDA神經網絡7.48 8.34 9.70 10.60 CRC1.50 1.561.58 1.57 2DPCA_CRC1.661.711.811.94

從表4中可以看出，本文算法的時間復雜度遠低于采用稀疏分類的PCA_LDA_SRC，略低于采用神經網絡分類的PCA_LDA_神經網絡，略高于2DPCA_CRC和CRC算法。但結合表1中的識別率可知，本文算法在略增加運行時間的同時大大提高了算法識別率，并增強算法穩定性，因此具有良好的應用價值。

再次，實驗還比較本文算法與其它類型的人臉識別算法[14]的識別率，見表5所示。

從表5中可以看出，除了在ORL數據庫中每類訓練樣本數r=7時，文獻[14]的DH-NMF算法的識別率略高于本文算法，其它情況下均是本文算法的識別率更高，尤其是在YALE數據庫下的兩種算法識別率的差別很大。這也證實本文算法受人臉圖像在光照、面部表情等方面的差異的影響較小，算法具有更好的穩定性。

表5 與文獻[14]算法的識別率比較
Tab.5 Comparison with the method of the literature[14]

r=3r=5r=7ORL數據庫PCA_LDA_CRC90.0793.6595DH_NMF82.991.295.4YALE數據庫PCA_LDA_CRC92.1494.9295.71DH_NMF75.078.383.3

最后，為了驗證算法在噪聲干擾下的魯棒性，實驗還測試了在樣本圖像中加入高斯白噪聲后算法的識別能力。圖1給出了ORL庫中的一個原始樣本圖像以及加入均值為0，方差分別為0.05、0.01、0.15、0.20、0.25的高斯白噪聲后的圖像。

圖1 原始人臉圖像和不同方差下的噪聲圖像
Fig.1 Original face image and noise images with different variance

表6比較了加入高斯白噪聲后，本文及其它幾種相關算法的人臉識別率。 用于實驗的樣本維數與表1相同。所有實驗結果均為測試10次的平均數。

表6 ORL人臉庫上的實驗結果
Tab.6 Test results on ORL face database%

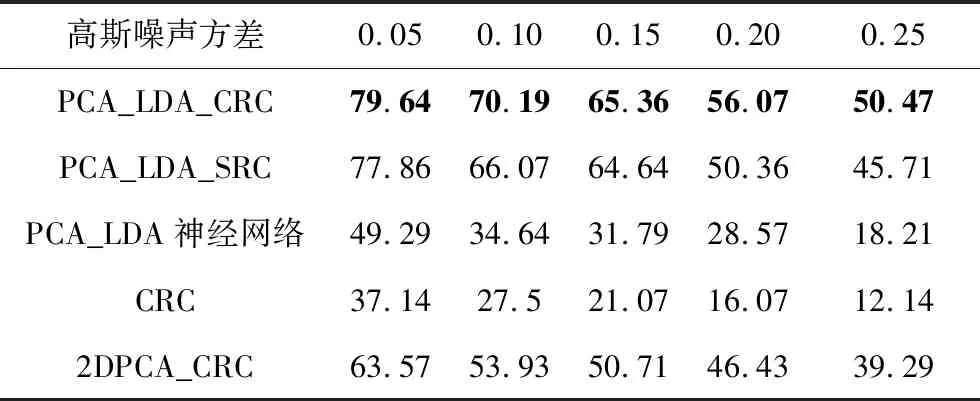
高斯噪聲方差0.050.100.150.200.25PCA_LDA_CRC79.6470.1965.3656.0750.47PCA_LDA_SRC77.8666.0764.6450.3645.71PCA_LDA神經網絡49.2934.6431.7928.5718.21CRC37.1427.521.0716.0712.142DPCA_CRC63.5753.9350.7146.4339.29

從表6中可以看出：當噪聲逐漸加強時，幾種算法的識別率都有所下降，但在同樣等級的噪聲干擾下，本文算法的識別率比其它幾種算法的識別率更高，抗噪能力更強。而PCA_LDA_SRC 和2DPCA_CRC算法在噪聲干擾下的表現一般，PCA_LDA神經網絡和CRC算法的抗噪能力則較差。

3 結論

本文提出了一種基于PCA_LDA降維和CRC協同表示分類的人臉識別算法。該方法融合了PCA算法、LDA算法和CRC算法的特點， 它能夠在有效提取樣本特征的同時，更準確的進行人臉分類。實驗證明，本文算法在三種常用的人臉數據庫上的測試結果穩定，能夠更好地消除光照條件、面部表情等方面的影響；相比其它幾種算法，本文所提算法在樣本維數較低，訓練樣本較少時，能夠在整體上獲得了更好的識別效果，而且該算法在外界噪聲干擾的情況下，識別率也一直較高，算法的抗噪性能較強。因此，本文算法具有良好的實用價值。