邊坡滲流與坡面徑流聯合求解三維有限元模型
王樂,田東方
(三峽大學水利與環境學院,湖北宜昌443002)
降雨特別是強降雨常常誘發邊坡失穩,王一超[23]等就降雨誘發土質邊坡失穩的成因進行了相關研究。由于邊坡巖土體的強度和受力等均與滲流場相關,因而強降雨時邊坡水分運移模擬是準確評價邊坡穩定性的基礎。但在強降雨條件下,除降雨入滲過程外,往往還伴隨坡面徑流;入滲與徑流過程相互影響,使問題變得十分復雜。
降雨時邊坡滲流模擬可基于Richards方程[1]實現。目前的各種分析方法中,在坡面未產流之前,將坡面視為流量邊界,流量大小即為降雨強度;坡面產流之后,根據對坡面徑流處理方式的不同,可以分為2類。
a) 忽略坡面徑流,將降雨入滲邊界視為定水頭邊界,水頭值等于地面高程[2-7]。這類方法的依據是:雖然坡面徑流增加了入滲水頭進而增大入滲率,但坡面水深往往很小,忽略這一水深(即認為水深為0)對入滲率影響不大。
b) 考慮坡面徑流,如采用運動波方程[8]或擴散波方程[9]描述坡面徑流,與滲流場耦合求解。根據耦合方式的不同,又可細分為2種方法。①以坡體滲流、坡面徑流兩場間的交換流量為聯系,采用迭代方法求解。基本思路是先假定兩場在坡面的交換流量,以此為邊界分別求解兩場,然后根據計算結果基于達西定律更新交換流量后再求解兩場,如此循環計算;以前后2次計算所得徑流水深是否足夠接近為依據結束迭代[10-14],這種方法可稱為迭代求解模型。②同樣以兩場間的交換流量為聯系,通過消去交換流量這一未知量,將滲流和徑流兩場同時求解;例如用徑流水深表示交換流量,然后代入滲流場邊界條件[15],又如把離散后的兩場方程組(例如有限元格式的離散方程組)相加消去交換流量[16-17];這種方法可稱為聯合求解模型。該方法要求在離散兩場控制方程時,對時間和空間的離散必須相同(詳見本文第3節)。
上述方法在處理某些特定問題時存在一定缺陷。以圖1為例,當滑床滲透性較小而滑體滲透性較大,在強降雨條件下邊坡AB段產流但BC段未產流,雖然AB段邊坡的徑流水深對該段邊坡降雨入滲影響較小,但雨水會流經至BC段邊坡而入滲。與坡面水深對滲流的影響相對應,本文將徑流的這種影響稱之為流量補給。第一類方法無法考慮該影響[18];文獻[19]通過修正流量邊界,建立了可以考慮流量補給的二維聯合求解模型。然而產匯流受地形影響較大,二維方法無法模擬三維情形下的產匯流過程。因此,本文在文獻[19]的基礎上開展進一步研究,建立了三維聯合求解模型。

圖1 典型滑坡剖面
1 基本理論
1.1 非飽和滲流控制方程
以各向同性和忽略源匯項的多孔介質飽和-非飽和滲流為例,基于質量守恒和達西定律的Richards方程[1]為:
(1)
式中C=?θ/?hs——容水度,L-1,這里表示非飽和土的容水度;θ——體積含水率;hs——壓力水頭,L;H=z+hs——總水頭,L;z——位置水頭,L;t——時間,T;K=KrKs——滲透系數,L/T;Kr——相對滲透系數;Ks——飽和滲透系數,L/T;x、y、z——空間坐標,L,z軸豎直向上為正。這里L、T分別表示長度、時間量綱。
初始條件為:
H(x,y,z,0)=H0(x,y,z)
(2)
簡單起見,邊界條件只考慮降雨入滲邊界S:
在未產流邊界S1上:
(3)
在產流邊界S2上:
(4)
式中H0——已知函數;R——降雨強度,L/T;nb——坡表內法線方向;I——入滲率,L/T;S=S1∪S2;S1∩S2=空集。
1.2 坡面徑流控制方程
采用運動波模型描述坡面徑流,該模型已被證實可用于模擬淺水和緩坡時的徑流過程[15]:
(5)
式中h——垂直于坡面方向的水深,L;x'、y'——位于坡面的坐標系;qn=Rcos(nb,z)-I——凈雨率,L/T;qsx'、qsy'——x'、y'方向的單寬流量,L2/T,由式(6)計算:
qsx'=C1h5/3;qsy'=C2h5/3
(6)

通常可認為初始時刻坡面無徑流;邊界條件為徑流上游邊界(分水嶺處)水深一直為0。
1.3 VG模型
非飽和滲流方程中的容水度C和相對滲透系數Kr可由土水特征曲線(SWCC)確定,常用的有VG模型:
(7)
(8)
式中Se——有效飽和度;θr——殘余體積含水率;θs——飽和體積含水率;a——VG模型擬合參數,L-1;n——VG模型擬合參數,m=1-1/n。
2 聯合求解模型的構建
2.1 求解域的離散
本文采用有限元離散滲流控制方程;采用特征有限元離散坡面徑流控制方程。只對滲流計算域劃分網格;徑流計算網格用滲流網格的坡表部分;兩場采用相同的空間離散。以圖2所示的一個單元為例,滲流網格單元為12 345 678,則徑流網格單元為1 234。同時,兩場也采用相同的時間離散。當坡面產流后,由于坡度較緩,垂直水深近似等于豎直水深,即式(1)中的hs近似等于式(5)中的h。因此,滲流場中坡表節點與徑流場中相同位置的節點在同一時刻具有相同水深,例如節點1、2、3、4等。

圖2 有限元網格
2.2 控制方程的FEM格式
Richards方程的有限元格式為:
(9)

運動波方程的特征有限元離散格式推導如下。式(6)可寫成:
(10)

(11)

式(11)變為:
(12)
設tk是時間的第k層,h=∑Nihi。式(12)的加權余量格式為:
(13)


ψ(x',y',tk)·

(14)

(15)
將式(14) 、 (15) 代入式(13) 并寫成矩陣形式:
(16)

2.3 聯合求解FEM模型的構建
由于H=hs+z,而hs近似等于h,則式(16)可寫成:
(17)
將式(9)、(17)等號兩邊對應相加:
(18)
進一步化簡為:
(19)
式(19)即為聯合求解模型的有限元格式。矩陣[A]只在產流的坡表單元上才不為0。

(20)

2.4 流量修正
坡面被離散為四邊形單元,見圖3。用h1、h2、h4、h5、h7和h8分別表示節點1、2、4、5、7和 8的水深。假設此時h1和h2為負值,而h4、h5、h7和h8為正;即單元I產流,而單元II未產流。此時,對單元II而言,邊界入滲流量將包括降雨、鄰近產流單元的徑流補給兩部分(如單元I)。此處以單元I為例說明徑流補給流量的確定方法。

圖3 補給流量的確定
首先根據節點水深由式(6)確定節點流量。例如節點4沿x'方向、y'方向流量,分別用q4x'和q4y'表示;節點5的2個流量分量也可同樣確定。則單元I經邊45流向單元II的水量隨之確定。單元II的其他臨近的產流單元也類似確定補給流量,設單元II的總補給流量為Qa,則單位面積補給流量為qa按式(21)計算:
qa=Qa/SII
(21)
式中SII——單元II的水平投影面積,L2。
計算時,每個時步內先通過式(19)計算滲流和徑流場,然后根據徑流結果按2.4節方法計算補給流量修正邊界條件后再次計算,直到前后兩次結果充分接近后再進入下一時步。
3 數值算例
以簡單邊坡為例,從累積入滲量的角度,說明當邊坡滲透性差異較大時,使用本文方法的必要性。計算域為平行六面體ACFDGINL,見圖4。ACFD為降雨邊界,降雨強度為R= 20 mm/h,持續10 h;其余為不透水邊界。初始體積含水率θ0為0.1。區域ABEDGHML為材料1;區域BCFEHINM為材料2。材料2的SWCC和滲透性函數數據見表1,飽和滲透系數用Ks2表示。簡便起見,材料1的飽和滲透系數為7.22×10-7cm/s,其余與材料2相同。

圖4 算例的幾何尺寸(cm)

表1 SWCC 與滲透性函數
分別采用本文方法和Geo-Seep模擬了不同Ks2時的降雨入滲過程。圖5為2種方法所得的累積入滲量(Q1、Q2)以及與累積降雨量RC的相對誤差(D1、D2)。其中,Q1、D1為本文方法結果;Q2、D2為Geo-Seep結果。

a) R=20 mm/h,Ks2=10-4 cm/s
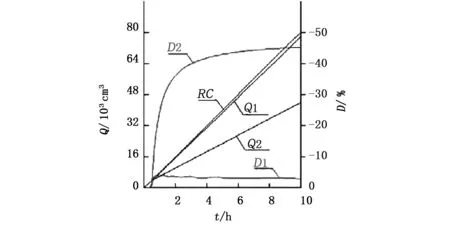
b) R=20 mm/h,Ks2=10-3 cm/s圖5 累積入滲量對比
圖5a表明,當下段邊坡滲透系數Ks2相對雨強較小時,不僅ABED段邊坡很快產流,而且BCFE段也很快產流,徑流對滲流的影響只有徑流水深,2種方法結果幾乎相同;說明了此時如果只關心入滲過程,忽略徑流是合理的。圖5b表明,當滲透系數Ks2相對雨強較大時,只有ABED段邊坡很快產流,而BCFE段未產流,徑流對滲流的影響除了徑流水深還有流量補給,本文方法更符合實際情況。此時如不考慮徑流補給,累積入滲量則只有累積降雨量的一半左右;可以推知,隨著產流區域(ABED)面積的進一步增大,誤差將更大。
4 結論與展望
a) 采用Richards方程描述邊坡飽和-非飽和滲流過程,采用運動波模型描述坡面徑流過程;分別采用有限元和特征有限元格式構建滲流、徑流控制方程的有限元格式;將2組有限元方程相加而消去交換流量,構建了邊坡滲流與坡面徑流聯合求解模型;根據徑流場修正入滲邊界流量。
b) 采用所建模型和Geo-Seep對簡單邊坡降雨入滲進行數值模擬,累積入滲量的對比表明:當上段邊坡滲透性相對下段邊坡較小,且上段邊坡產流而下段邊坡未產流時,本文方法所得的累積入滲量更加符合實際情況。

