基于可變模糊集模型的渭河流域水質監測

劉 嶸

(甘肅省天水水文水資源勘測局，甘肅 天水 741000)

作為我國黃河最大支流，渭河全長818km，流域總面積134766km2，渭河流域主要分為甘肅省段與陜西省段，流域范圍較廣，水系復雜且不對稱，擁有較多支流[1]。從俯視圖上可以清楚地看出秦嶺北坡的徑流深隨山地高程升高而增加，由低于100mm到高于600mm，最高中心在太白山及南五臺山。渭河沖積平原十分平坦，水利化程度很高，屬于低產流區[2- 3]。渭河流域人口密集，耕地資源豐富，且渭河支流部分存在許多工業基地。隨著我國工業產業的飛速發展、人口數量的激增，生活污水、工業污水大量排放，造成水體嚴重污染，極大影響了生態功能和區域經濟發展。因此，環保部門和水質監測部門極其重視河流水體污染問題[4]，確保渭河流域能夠可持續發展，實現水資源的科學合理利用，實現社會、資源、環境以及經濟的協調發展。本文基于可變模糊集模型對渭河流域的水質進行監測，了解渭河流域水質具體情況，為渭河流域水體保護、水污染治理提供數據參考。

1 渭河流域水質調查情況

近年來全國各地水體嚴重污染，針對這一情況對渭河流域水質進行調查，發現陜西省的居住人口都集中在渭河流域，另外還有很多發展迅速的工業基地，緊鄰渭河支流[5]。據統計，渭河流域人口占全省人口的61%，工業企業千余家，無論是城市污水還是工業廢水，都經支流最終排入渭河。因此，基于可變模糊集模型對渭河流域水質進行監測是十分必要的，有助于詳細了解渭河流域水質現狀，并做出針對性的治理和保護[6- 7]。

2 基于可變模糊集模型的水質監測

陳守煜教授創建的模糊集合理論是可變模糊集模型的基礎性理論，也是可變模糊集模型的核心。基于模糊集合理論，并結合相對隸屬度處理連續隸屬、指標動態變化及模糊邊界情況[8]。通過變換模型參數指標來完成變量間的線性模擬或非線性模擬。

可變模糊集理論包含了隸屬函數和自然辯證法，不僅被應用于實際工程領域，更被廣泛應用于水文水資源學中。可變模糊集模型可綜合多個指標，對渭河流域水質樣本進行客觀、科學地監測，能夠更加準確地獲取該流域內水質狀況。也能夠為渭河流域水體保護和水污染治理提供依據[9- 10]。本文把可變模糊集模型應用于渭河流域水質監測中，具體步驟如下。

2.1 水質監測樣本處理

(1)

式中，xij—j水質樣本、i指標的特征值，i可取值1，2，…，m；j可取值1，2，…，n。m—指標特征數量；n—待監測水樣數量；X—指標特征矩陣。

(2)

式中，yih—i指標h級別的標準值，h可取值1，2，…，c；Y—構成m×c型指標的標準特征值矩陣。

2.2 可變模糊集模型建立

設立具有代表性的水質監測點，通過對關鍵點的監測了解水域整體水質空間分布特征情況：

(3)

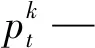
(4)

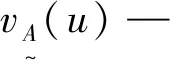
(5)

(6)

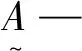
2.3 水質監測

由于指標存在量綱，且指標變化方向不統一(透明度、溶解氧為逆指標，總磷、總氮為正指標)，利用下列公式規劃水質監測樣本和標準。

(7)

(8)

式中，rij—j水質樣本i指標對監測的相對隸屬度；Sih—i指標的h級標準特征值的規劃結果。計算渭河流域水質檢測樣本與標準的廣義指標權距離，即可求出所監測水質樣本j在水質標準級別h中的相對隸屬度uhj。

(9)

式中，h—水質標準級別，取值1，2，…，c；aj—監測水質樣本的下限值；bj—監測水質樣本的上限值。

通過模型參數可以模擬指標與標準間的不同關系，一般a，p可分下列4種關系：

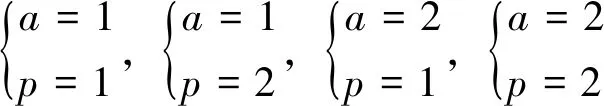
(10)

把式(9)求得的相對隸屬度uhj代入式(11)中，即可得出渭河流域監測水樣j的綜合監測級別。

(11)

式中，H—監測水樣的綜合監測級別，其他系數同上述公式。用此可變模糊集模型來監測渭河流域水質情況，經分析研究，統計數據可用于渭河流域水體保護和污染治理。

3 監測結果及分析

為了驗證基于可變模糊集模型對渭河流域水質監測的準確性，以渭河流域總磷已知濃度和錳元素已知濃度為參考標準，與原子吸收分光光度法做對比，經過多次實驗，得出渭河流域總磷濃度監測對比(如圖1所示)和渭河流域錳濃度監測對比(如圖2所示)。

圖1 渭河流域總磷濃度監測對比

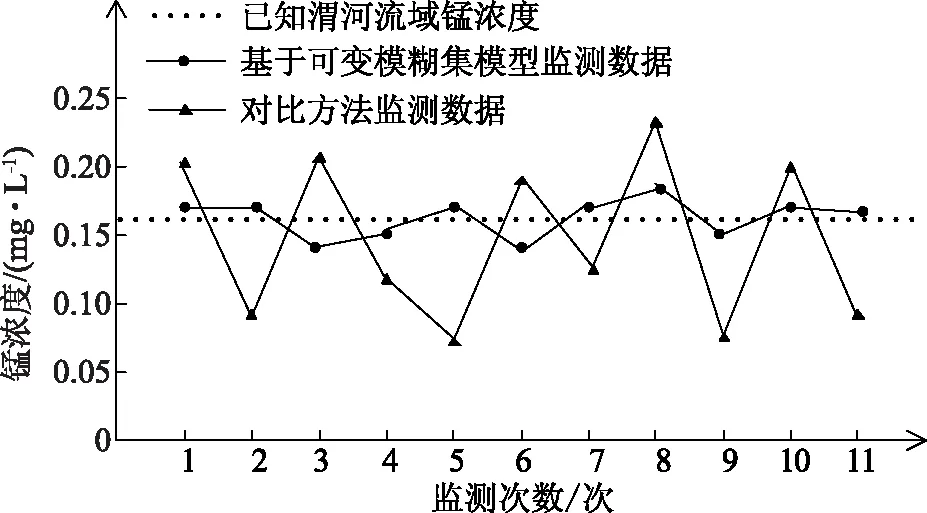
圖2 渭河流域錳濃度監測對比

經過實驗對比驗證發現，基于可變模糊集模型對渭河流域總磷濃度和錳濃度的監測數據更接近已知濃度，而對比試驗使用原子吸收分光光度法進行監測的數據則偏離已知濃度較遠。由此可知，本文提出的基于可變模糊集模型對渭河流域水質監測相較于其他監測方法更為準確，有助于實時掌握渭河流域水質狀況，更適合應用。對于水體保護和治理水體污染具有重要現實意義。

4 結語

由于渭河流域附近工業廠房較多，居住人口密集，導致近年來渭河流域水質污染嚴重，由于水質監測結果的不準確給水體治理帶來了難度和阻礙。為了更準確掌握渭河流域水質狀況，基于可變模糊模型對渭河流域水質進行監測。經過對比驗證，發現該方法的監測數據結果更為準確，提高了渭河流域水質監測工作的效率，說明該方法的有效性和快捷性。希望為水質監測提供方法參考和依據，為治理水體污染提供準確的數據保障。