電廠溫排水熱擴散三維數值模擬研究
佘格格
(三峽大學水利與環境學院,湖北 宜昌 443002)
溫排水是指電廠冷卻水中溫升約10℃并經由電廠重新排回自然水體的那部分水,會引起工程附近河道水體溫升變化。同時溫排水擴散引起的取水溫度升高會降低機組的效率,甚至由于過度的熱回歸效應而導致停機[1]。溫排水擴散問題涉及取排水平面布置,是工程的一個核心技術問題。因此,溫排水溫度三維分布的研究對指導電廠設計與控制水體污染等方面具有重要的現實意義。
1 三維數學模型建立
1.1 控制方程
為適應水域床面和自由表面變化緩慢,選用σ坐標描述淺水流動和溫度輸運三維數學模型。這樣數值離散與計算過程中,計算域在垂向可以分為相同的層數,帶來了網格剖分和數值離散的方便[2]。同時在σ坐標下可以精確地給定床面和水面的邊界條件,使結果在垂向有較高的分辨率。
1.1.1三維水流運動方程
笛卡兒坐標系下的水流運動控制方程為:
(1)

(2)

(3)
其中,

(4)
(5)
(6)
式中,u、ν、w—在x、y、z方向的流速分量;w—通過某一σ坐標層的流速;h—水深;f—柯氏力系數,f=2ΩsinΦ;Ω—地球旋轉角速度;Φ—地理緯度;g—重力加速度;ρ—水體密度,密度為溫度和鹽度的函數,ρ=ρ(T,S);ρ°—參考密度;A—水平紊動黏性系數;νt—垂向紊動黏性系數;pa—大氣壓強;us、vs—排入環境水體中的水流流速;S—點源流量。
1.1.2溫度運輸方程

(7)
(8)

1.2 初始條件
計算水動力時,初始時刻水域各點初始溫升取為0或是取水口溫升值對結果精度影響不大。所以模型初始流速均設置為0,初始水位為計算條件中各時期河段平均水位。模型邊界由自由表面與床面組成。水氣界面上的流速邊界條件由假定給出。自由表面處溫度由表面散熱條件確定,床面溫度滿足絕熱條件。
2 數值計算方法
研究采用基于非結構三角形網格的有限體積法求解溫排水運動的數學模型[4- 6]。為了適應地形的復雜變化,研究中采用非結構三角形網格對計算區域進行離散,選用網格中心式的有限體積法離散控制方程。求解三維水流模型時,時間積分采用半隱格式,將水平項的時間積分采用二階龍格庫塔格式,垂直項的時間積分采用二階隱式梯形格式。在三維溫度運輸方程的求解中,將水平與垂直非黏性項采用二階龍格庫塔格式,垂直黏性項采用二階隱式梯形格式積分。
3 模型驗證
在驗證計算時采用某電廠實測資料。驗證內容包括水流驗證及水溫驗證,水流驗證內容有水面線、斷面流速分布和分流比驗證。
水文測驗沿程共布設6個水尺,實測期間沿著計算河段布置了CS1~CS5共5個,在排水口上下游布置了3個采樣點,分別位于排水口上游50m、排水口末端中點和排水口下游500m處,進行同期垂線點溫升觀測,具體布置情況如圖1所示。電廠已建2×300MW機組,夏季用水量約25.0m3/s,排水溫升約9.0℃;冬季用水量約15.0m3/s,排水溫升約14.0℃。共布置了20330個網格節點和39430個計算單元,在垂直方向對水體進行分層,層數為20。

圖1 各斷面布置
3.1 水位驗證成果
采用實測的水面線資料(21900m3/s)進行糙率率定,采用水面線資料(Q=11700m3/s)進行水面線驗證,其成果見表1。

表1 水位驗證成果 單位:m
3.2 斷面流速驗證成果
由于篇幅限制,圖2為流速計算值與實測值對比圖,表2為計算與實測垂線平均流速對比表,統計得到各斷面上不同測點流速計算值與實測值間誤差一般均在0.10m/s內。

圖2 流速計算值與實測值對比
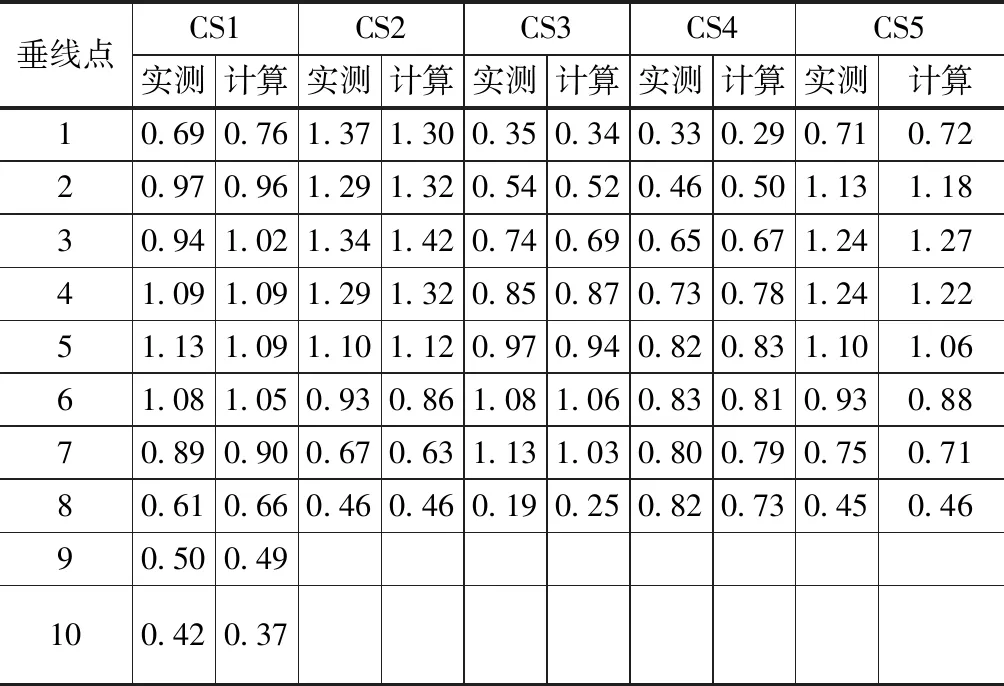
表2 測流斷面計算與實測流速對比單位:m/s
3.3 汊道分流比驗證
對測流時汊道分流比進行了驗證,見表3。由表3可見,汊道分流比誤差均在1%內,說明汊道分流比驗證較好。
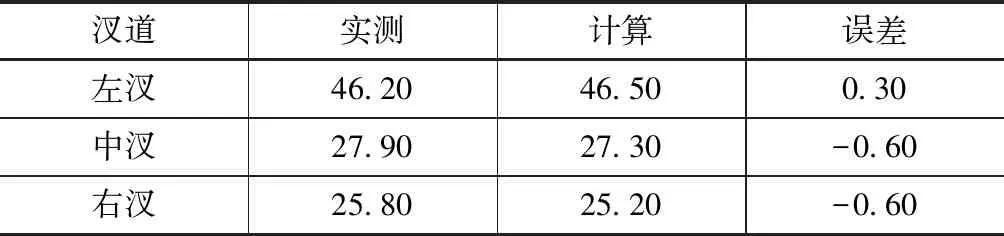
表3 汊道分流比驗證 單位:%
3.4 溫升分布驗證
將計算溫升與實際測得溫升進行比較見表4。可以看出排水口上、下游采樣點溫升驗證均較好,而排水口處采樣點誤差稍大,總體而言,計算值與實測值大部分吻合。

表4 溫升分布驗證 單位:℃
由以上結果可見,模型能夠較好地模擬整個計算河段的水流運動與溫度場分布。
4 結語
采用的三維溫排水數學模型較好地模擬了計算河段的水流運動,水面線過程、斷面流速分布及汊道分流比驗證較好,并采用實測資料對模型溫度場進行了驗證,數學模型計算方法可行,參數取值合理,可為類似情況提供工程參考。

