一種用于超聲成像的零相位濾波后處理方法?

韓曉麗 吳文燾 曹 政

(中國科學院聲學研究所 北京 100190)

0 引言

超聲相控陣系統中，聲波信號在經過隔離、限幅、放大、濾波等模擬調理電路時必然會引入一定的噪聲干擾[1]，因此，由A/D 采樣后的數字信號在成像之前，必須要經過一定的濾波處理，以提高信噪比和成像質量[2?3]，也就是說，濾波是一個必備的處理過程。在對接收的回波信號進行分析的過程中，通常需要將信號不同成分進行分離，然后對不同成分做不同的處理或調整，從而最終提高對于缺陷或目標的檢測能力[4]。大部分具有頻率依賴性的檢測識別算法的實現都需要輔以濾波處理的過程，包括超聲檢測系統廣泛采用裂譜處理(Split spectrum processing, SSP)方法，從本質上講，也是采用若干帶通有限脈沖響應(Finite impulse response, FIR)濾波器進行濾波的過程[4?5]。

在超聲無損檢測領域，超聲波遇到缺陷時會發生散射，在接收端會接收到經缺陷散射的回波信號，與缺陷有關的信號出現的時間即到達時間(Time of arrival, TOA)或傳播時間(Time of flight, TOF)[4]恰恰能夠反映缺陷在檢測對象中所處的位置，以此來對缺陷進行定位。同時，為了保證系統檢測的靈敏度和能夠通過缺陷回波幅度在一定程度上估計缺陷的大小，要求缺陷回波波幅在濾波前后保持不變。基于上述兩點，在對接收的回波信號進行濾波處理時，要保證濾波過程不影響主要頻率成分的到達時間，這就需要濾波器具有零相位的相位響應特性。雖然FIR濾波器在單位脈沖響應序列h(n)滿足一定的對稱性時，具有線性相位特性[6?7]，但是濾波前后必然會出現一定的時延，難以滿足零相位的要求。而無限脈沖響應(Infinite impulse response,IIR)濾波器不能實現嚴格意義上的線性相位特性。

除了直接設計具有零相位響應的數字濾波器以外，零相位濾波的過程還可以通過一種比較巧妙的方式實現，即采用前向-后向濾波-反向輸出(Forward-reverse filtering, reverse output, FRR)[8]或反向濾波-反向輸出(Reverse filtering,reverse filtering,RRF)的方法[9?10]。這種方法借助于兩次濾波和信號翻轉的組合，實現對輸入信號的零相位濾波。鑒于FIR濾波器具有便于實現線性相位特性的優越性、系統穩定性好和使用上的靈活性[11]，通常大家習慣性地選用FIR 濾波器實現濾波過程，包括零相位濾波，也主要以FIR 的方式實現[10]。然而，由于FIR 濾波器傳遞函數的極點固定在原點，只能靠改變零點位置來改變它的性能。所以要達到高的選擇性，必須用較高的階數；對于同樣的濾波器設計指標，FIR 濾波器所要求的階數可能比IIR 濾波器高5～10倍，信號延時也較大，處理效率低[11]。

近年來，在超聲檢測領域，實時缺陷檢測的需求越來越高，要求系統能夠盡快地實時采集、分析和處理超聲波回波信號，這對于超聲成像系統的實時性提出了更高的要求[5]。許多學者致力于探索如何高效地實現超聲回波信號采集之后的濾波過程[12]，也包括開辟濾波器的高效硬件實現的新思路[5,10]。快速高效地實現零相位濾波，將有利于超聲檢測系統信號處理效率的提升，確保檢測系統具有更高的實時性能。

本文針對在超聲相控陣成像領域，在采用基于FIR濾波器的FRR零相位濾波時，由于FIR濾波器階數高導致運算量大、處理效率低、難以滿足實時性要求高的系統需求的問題，探討在實際超聲相控陣系統中使用IIR 濾波器實現FRR 零相位濾波的可行性，比較基于FIR和IIR 濾波器實現FRR零相位濾波的性能，探索IIR 濾波器實現FRR 零相位濾波時的效率提升程度，并且把IIR 零相位濾波應用于實時超聲成像后處理系統中，通過實際的成像實驗，驗證使用IIR 濾波器實現FRR 零相位濾波的效果。

1 基于IIR的零相位濾波

根據線性系統理論，對信號進行經典線性濾波的過程對原始輸入信號主要產生兩大方面的影響[9]：一是對信號不同頻率成分的幅值進行調整，通帶內的頻率成分一般不衰減甚至得到放大，而阻帶內的成分通常被衰減，以減少這些成分在原始信號中所占的比重或影響，這是通過濾波器的幅頻響應來實現的；二是對信號的不同頻率成分產生相應的相移，這是通過濾波器的相頻響應Arg[H(ejw)]來實現的。濾波器的線性相位指的是不同頻率成分的時間延時是相同的，則總體上輸出信號相對于輸入信號不發生相位失真，僅發生一定的延遲。在超聲相控陣成像系統中借助于零相位濾波正是巧妙地實現了對超聲回波信號的濾波處理，同時保證群延時為零，即處理后的回波信號仍具有正確的到達時間。

借助于兩次濾波和信號翻轉的組合以實現零相位濾波的具體方法有兩種：FRR 和RRF。FRR零相位濾波過程如圖1所示。設濾波器單位脈沖響應序列h(n)，對應的Z變換(Ztransformation)為H(Z)。FRR先將輸入序列x(n)按順序輸入到濾波器H(Z)中進行濾波，即前向濾波；然后將所得的結果序列y1(n)，翻轉后得到序列y1(?n)，y1(?n)再次輸入到濾波器H(Z)中，即反向濾波；再將所得結果y2(n)逆轉后輸出，即反向輸出；最后得到精確的零相位失真的輸出序列y(n)。RRF 先將輸入信號序列反轉后通過濾波器，然后將所得結果逆轉后再次通過濾波器，這樣所得結果即為精確零相位失真的輸出序列[9]。不管是哪種具體方法都需要預先設計具有特定幅頻特性的濾波器H(ejw)。

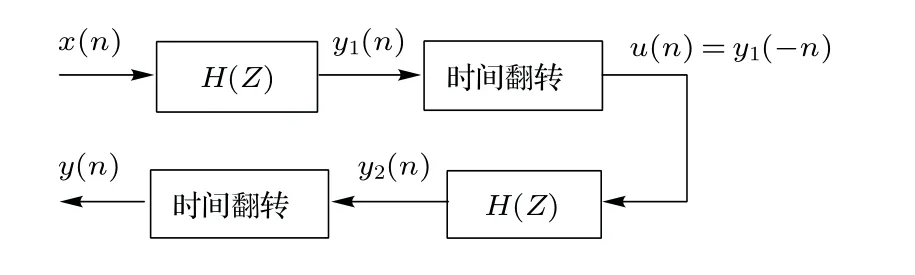
圖1 FRR 零相位濾波過程Fig.1 Zero phase filtering based on FRR

FRR簡單的推導過程[5]如下：

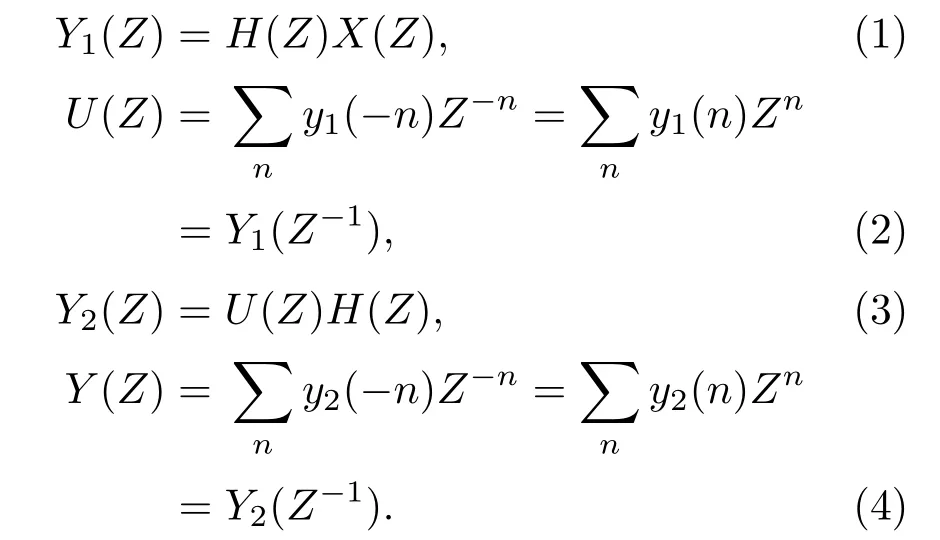
聯立以上4 式，可以推得整個零相位過程的等效傳輸函數Heq(Z)：

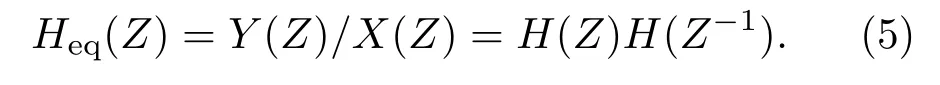
即等效系統頻率響應為

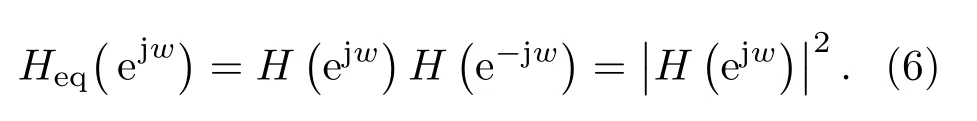
也就是說，FRR 濾波過程真正實現了對輸入信號x(n)的群延時為零的濾波處理，僅對其各頻率成分進行了幅度調整。RRF 的推導過程與FRR 類似，這里不再贅述。因此，設計零相位濾波時，主要是設計滿足特定需求的具有特定幅頻響應特性的基礎濾波器H(Z)。在上述推導過程中，并未指定濾波器H(Z)為有限脈沖響應濾波器(FIR)還是無限脈沖響應濾波器(IIR)。本文在后續章節中，將基于FIR 的FRR零相位濾波稱為FIR FRR，將基于IIR的FRR零相位濾波稱為IIR FRR。

2 IIR FRR零相位濾波的設計與分析

FRR 或RRF 的過程對輸入信號的相位最終不產生影響，因此我們在設計基礎濾波器H(Z)時主要關注其幅頻特性，使其幅頻特性滿足我們的具體應用需求即可。下面以帶通FRR 零相位濾波為例，設計IIR FRR和FIR FRR的基礎濾波器H(Z)。FIR FRR主要用于與IIR FRR進行對比。

2.1 基礎濾波器的設計

分別設計幅頻特性參數如表1所示的FIR 和IIR 濾波器。前者采用等波紋(Equiripple)法，后者采用契比雪夫II (Chebyshev II)法。

設計的FIR 和IIR 濾波器的幅頻響應曲線如圖2所示。前者為57階，即N=57，后者為12 階，即N=12，其中Nb=12。在表1所示的幅頻響應特性參數的約束下，兩種情況設計的幅頻響應曲線在通帶內的形狀差不多，主要差異在于低頻范圍內的通帶到阻帶的過渡帶上，IIR 濾波器更窄。其中IIR 濾波器的零極點分布如圖3所示。距離單位圓最近的極點是0.9484±0.2190 i。

表1 帶通濾波器幅頻特性描述參數Table1 Bandpass filter amplitude-frequency characteristic parameters

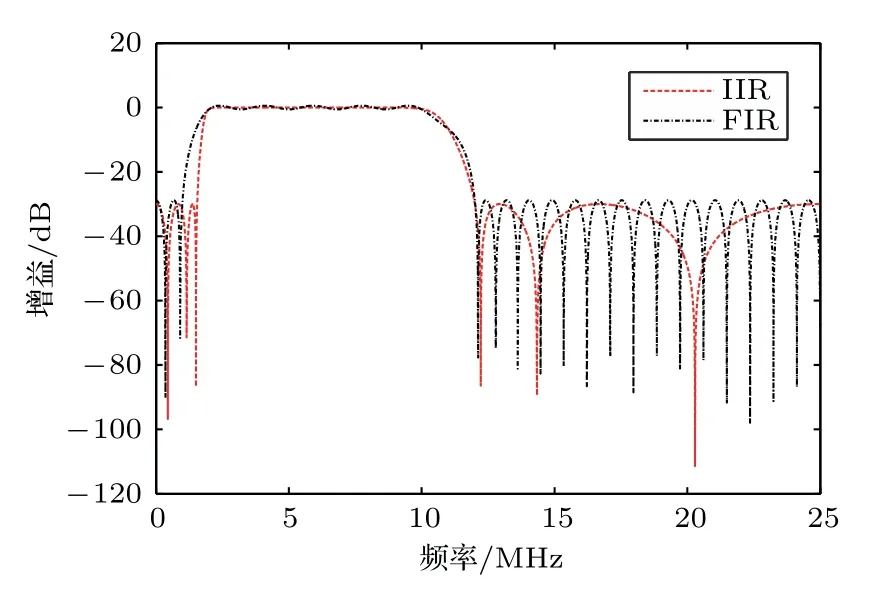
圖2 IIR 和FIR 濾波器幅頻特性曲線Fig.2 Amplitude-frequency curves of IIR and FIR filters

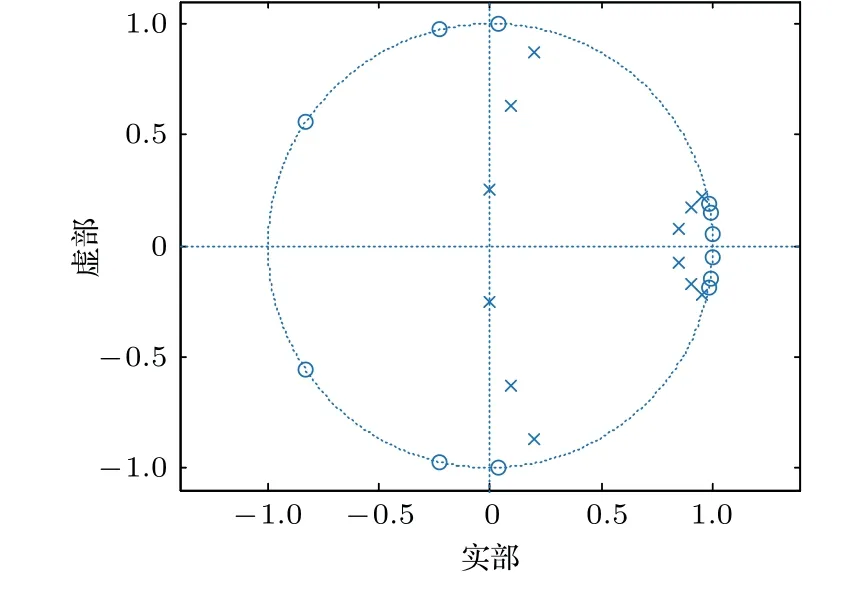
圖3 IIR 濾波器零極點圖Fig.3 Pole-zero diagram of IIR filter

2.2 FRR運算量分析

設x(n)為長度為Nx的因果序列， 即n ∈[0,Nx ?1]。對于一個N階的直接型FIR 濾波器，根據公式(7)可以推知，完成N階的FIR 濾波需要的運算量為(N+ 1)(Nx ?N+1)次乘法，N(Nx ?N+1)次加法。

對于一個N階的直接I 型IIR 濾波器，根據遞推公式(8)可以推知，完成N階的IIR 濾波需要的運算量[13]為(N+Nb+1)(Nx ?N+1)次乘法，(N+Nb)(Nx ?N+1)次加法。其中，Nb為IIR濾波器傳輸函數H(Z) 的分子多項式的階數，需要注意的是，這里假定兩種情況下輸出序列的長度都僅取決于已知的輸入序列x(n)和濾波器階數，即輸出序列y(n)的序列號范圍均為n ∈[N,Nx]。

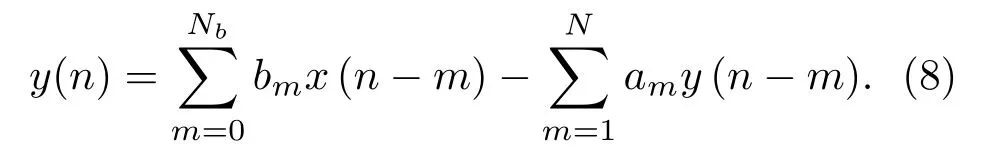
因此，上述的57階FIR和12階IIR濾波器直接I 型實現時的運算量如表2所示，其中，輸出序列長度Ny=16384，輸入序列長度Nx=16384+N ?1。由此看出，理論上，前者的運算量約是后者的2倍多。

表2 FIR 和IIR 運算量理論值Table2 Amount of calculation comparison between FIR and IIR

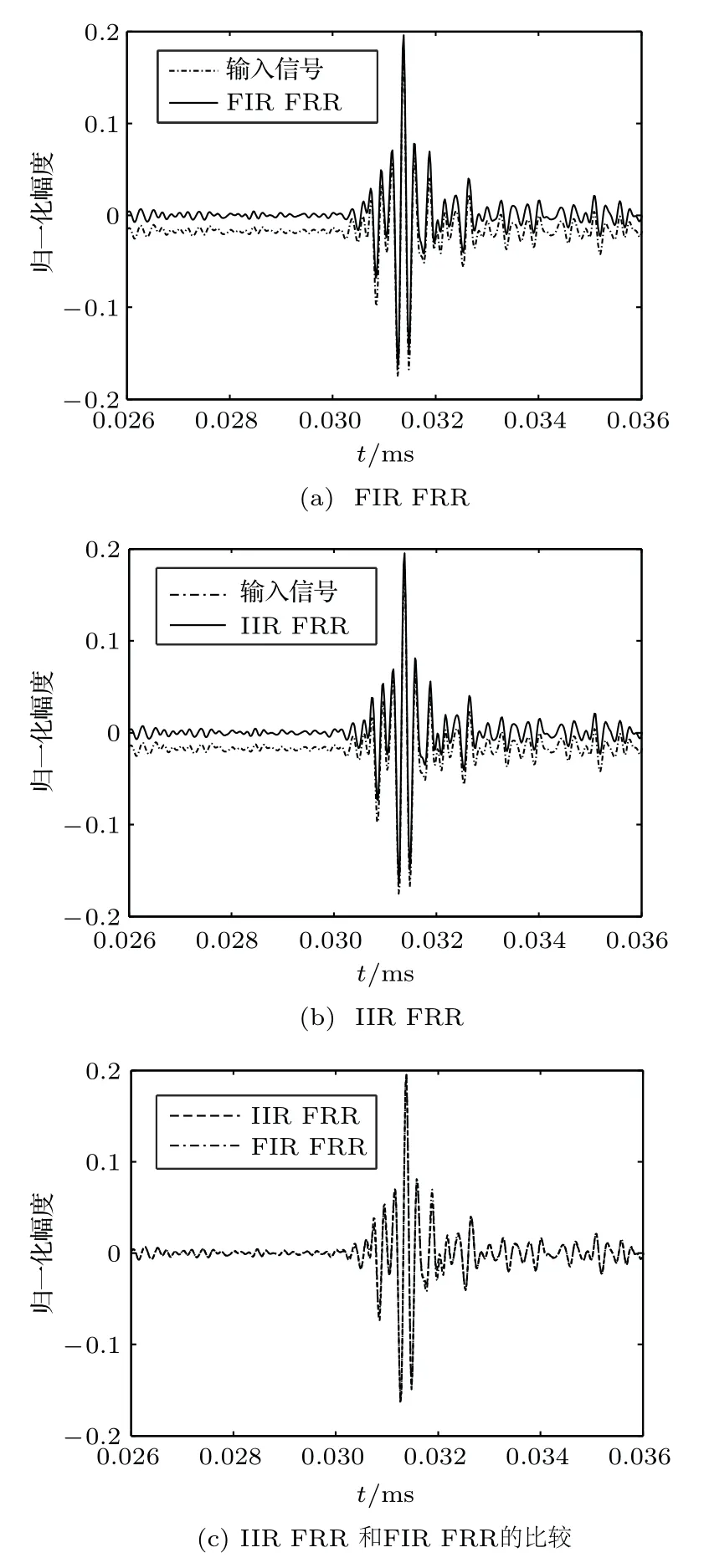
圖4 FIR FRR 和IIR FRR 零相位濾波結果比較Fig.4 Comparison of zero-phase filtering results of FIR FRR and IIR FRR

在Matlab 中，利用設計的FIR 和IIR 濾波器對射頻回波信號進行FRR 零相位濾波處理，對原始回波信號進行FIR FRR 和IIR FRR 的濾波結果如圖4(a)和圖4(b)所示。由圖4可知，IIR FRR同FIR FRR 一樣，也可以實現零相位濾波的功能。濾波前后，FIR FRR 和IIR FRR 的細節比較如圖5所示，兩種情況輸出信號的時間位置相同，在幅度上只有較小的差異，造成差異的原因是兩種濾波器的幅頻特性曲線并不是完全相同的。因此，在幾乎一致的幅頻響應特性情況下，FIR 濾波器的階數約為IIR濾波器階數的5 倍，理論上的運算量約是IIR 濾波器的2倍多。

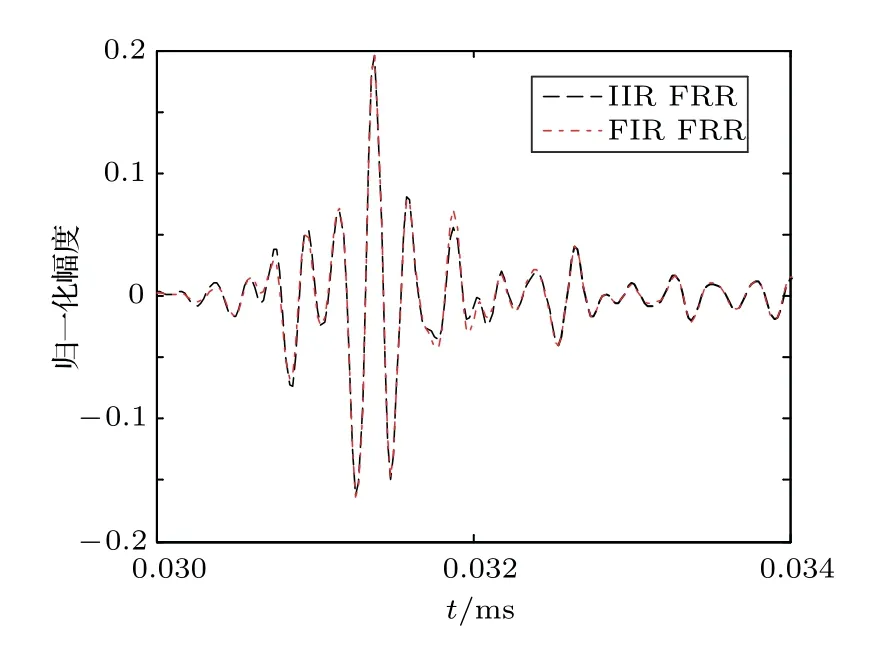
圖5 FIR FRR 和IIR FRR 濾波結果的細節比較Fig.5 Detailed comparison of FIR FRR and IIR FRR results

3 IIR FRR用于超聲成像后處理

為了比較IIR FRR 和FIR FRR 的超聲成像效果，設計兩組成像實驗，分別利用FIR FRR 和IIR FRR對原始信號進行零相位濾波，然后經過相同的其他后處理后獲得超聲成像結果，并對結果進行比較。從原始數據到成像的整個后處理過程如圖6所示。兩組成像實驗分別為：(1)單孔成像，(2)多孔成像。采用由課題組自主研發的UA special I 超聲相控陣系統采集一幀原始回波數據，采集時使用的試塊和換能器的放置形式如圖7和圖8所示。圖7中，試塊在深度25 mm 處有一個直徑為1 mm 的通孔，相控陣換能器通過耦合劑與試塊表面直接耦合，聚焦深度為25 mm。圖8中的試塊為標準的B 型便攜式相控陣試塊，由濟寧模具廠生產，檢測時換能器中心位于18??2 排孔最左側兩個孔的中間連線上，以18??2排孔為檢測時的主要目標，聚焦深度設為50 mm。數據采樣率為50 MSPS，超聲相控陣換能器中心頻率為5 MHz。

圖6 超聲成像后處理過程Fig.6 Post-processing of ultrasonic imaging involving zero-phase filtering

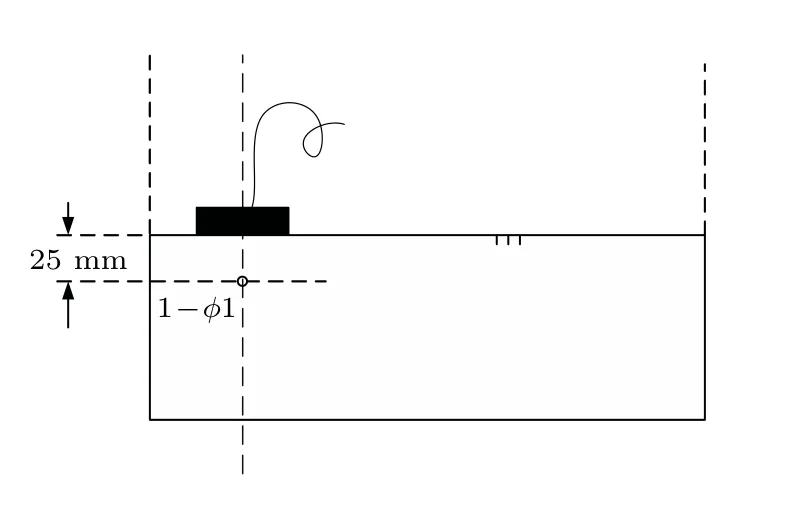
圖7 數據采集時試塊和換能器位置示意圖——單孔Fig.7 Test block and transducer position during data acquisition (single hole)

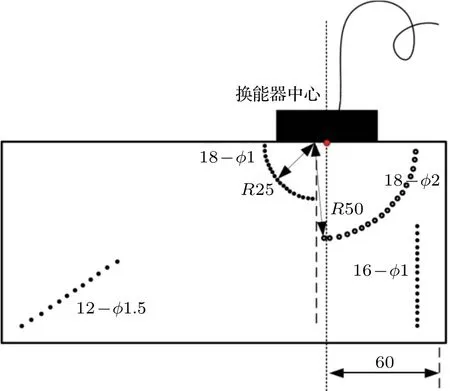
圖8 數據采集時試塊和換能器位置示意圖——多孔Fig.8 Test block and transducer position during data acquisition (a row of holes)

3.1 基于IIR FRR 的超聲成像

利用圖7情況下采集的回波數據集，經過圖6所示的處理過程，其中的零相位濾波的過程分別利用FIR FRR 和IIR FRR 完成，最終形成如圖9所示的單孔成像結果。由圖9可知，經FIR FRR 和IIR FRR 處理后的數據的成像效果幾乎完全相同，視覺上難以分辨差異。

圖9 FIR FRR 和IIR FRR 成像結果——單孔Fig.9 Imaging based on FIR FRR and IIR FRR (single hole)

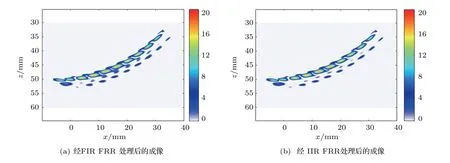
圖10 FIR FRR 和IIR FRR 成像結果——多孔Fig.10 Imaging based on FIR FRR and IIR FRR (a row of holes)

另外，利用圖8情況下采集的回波數據集，經過圖6所示的處理過程，其中的零相位濾波分別利用FIR FRR 和IIR FRR 完成，最終對18??2 排孔形成如圖10所示的成像結果。由圖10可知，在復雜的多孔成像情況下，經FIR FRR 和IIR FRR 處理后的數據的成像效果也幾乎完全相同，僅在18??2后方的偽影處存在極其細微的差別，這是由于兩種濾波器的幅頻特性曲線并不是完全相同導致的。

由成像結果可以看出，IIR FRR 可以實現與FIR FRR幾乎相同的零相位濾波性能，得到幾乎一致的超聲成像效果。

3.2 算法實時性的驗證

系統后端采用8 核處理器TMS320C6678 進行處理，利用定時器統計連續執行1000 次FIR FRR和IIR FRR 零相位濾波的時間，然后計算平均一次FRR 零相位濾波的時間。57 階FIR 和12 階IIR 采用直接I 型網絡結構實現，數據格式采用浮點格式，其中，輸出序列y(n)的長度Ny= 16384，輸入序列x(n)長度Nx=16384+N ?1。統計結果如表3所示。需要注意的是，在統計時間時，保持兩種濾波過程采用相同的程序結構來實現，保證調用相同的函數，以及在調用函數時保證采用相同的調用格式，以保證在兩種情況下，濾波算法的結構、實現的具體方式是相同的，從而盡可能減少其他因素對處理時間的影響。

從表3中可以看出：基于12 階IIR 的FRR (直接I) 比FIR FRR (直接I) 耗時少，后者是前者的1.71 倍。

表3 FIR FRR 和IIR FRR 耗費的時間對比Table3 Time consumed during FIR FRR and IIR FRR

4 討論

(1)處理時間

從理論角度分析，實現幅頻響應類似的濾波，IIR 確實相比FIR運算量低很多，如表2所示。保守來講，IIR甚至僅為FIR的1/2。

由表3可知，采用直接型I 結構實現高階IIR 濾波器時，相對于采用直接型結構的FIR，IIR FRR的處理效率優于FIR FRR。對比表2和表3，相比基于57 階FIR 的FRR，基于12 階的IIR(直接I 型)的FRR 處理時間確實更短，但并沒有達到約2 倍多的處理效率的提升。這是因為FRR 的過程包括兩次濾波和兩次序列的翻轉，濾波耗時只是FRR處理總時間的一部分，在硬件處理器上執行FRR算法的時間，不僅包括完成兩次FIR 或IIR濾波的時間，還包括序列翻轉的時間。這些時間導致最終統計的時間效率比值不可能達到實現IIR 和FIR濾波器本身的時間效率比。

(2)穩定性

由于IIR 濾波器存在極點，如圖3所示。當極點取值在單位圓內時，理論上IIR 濾波器是穩定的。但是在硬件處理器上實現時，濾波參數的量化或截斷效應可能會引起實際濾波器極點位置的偏移，從而會引起濾波器出現不穩定的情況。在定點處理器中，這種問題尤為突出。但是FIR 濾波器由于只存在零點，不會出現不穩定的問題。從這個角度上說，FIR 濾波器實現起來更容易，更穩定，對參數數據占位寬度或精度的要求更低。因此基于IIR 的FRR更適用于浮點處理器。

5 結論

基于IIR FRR 零相位濾波可以實現與FIR FRR 相當的處理效果。當IIR 濾波器采用直接I型結構直接實現時，相對于FIR FRR，IIR FRR 可以在保證成像效果的前提下，將處理效率提升近1倍。在實際實時超聲成像系統中，為了獲得更高的處理效率，實現更高的幀率，可以選擇采用IIR FRR零相位濾波取代FIR FRR。尤其在浮點型硬件處理器中，采用直接型IIR 實現FRR 零相位濾波，可以一定程度上提高處理效率。在實際應用中，需要仔細權衡FIR FRR 和IIR FRR 零相位濾波器在性能、時效、精度、穩定性、可控性、占用內存等多方面的要求，合理選擇采用何種方式實現零相位濾波處理。