小振幅振動翼型升力遲滯環變向的成因分析
薛臣,周洲,*,李旭,許曉平
1.西北工業大學 航空學院,西安 710072 2.西北工業大學 無人機特種技術重點實驗室,西安 710065
隨著航空技術的發展,飛行器的應用范圍變得越來越廣泛,因此面臨的問題也更加復雜。近幾年,人們越來越重視綠色航空,太陽能無人機由于其自身獨有的特點越來越受到人們的重視,如美國的太陽神[1-3]、英國的西風[4-5]。此外,谷歌和Facebook也都宣布了各自的太陽能無人機計劃。太陽能無人機因為受限于目前能源利用率較低的因素,一般展弦比很大,呈現超輕面密度的結構特點,所以太陽能無人機在飛行中會面臨較嚴重的振動問題,研究這一問題對指導太陽能無人機設計有重要意義。
在翼型振動方面,目前多數學者的研究重點都在大迎角運動和增升機理方面。大迎角俯仰振蕩研究方面現在主要集中在翼型動態失速研究,Albertson等[6]、Helin和Walker[7]通過實驗發現翼型前緣加速側會出現動態失速渦(文獻[8-9]中也叫前緣渦),在低雷諾數條件下,這個渦會顯著提高升力。文獻[10-11]也指出對于撲翼來說,這個動態失速渦會在增升方面扮演著重要的角色;Leknys等[12]采用粒子圖像測速(PIV)對NACA0021翼型的動態失速問題進行研究,發現翼型的轉動造成了翼型的升力有一個明顯的延遲現象,而且可以將翼型的整體分離流動出現的角度推遲到60°。
注意到在翼型的大幅振蕩研究中,已經發現翼型的振動會推遲翼型的失速迎角,這種由翼型振動帶來的遲滯現象也吸引了很多學者的注意。實際上,這種非定常效應引起的遲滯效應與很多因素有關,例如振動頻率,振動軸位置和振動幅度等[13],Jung和Park[14]發現在低雷諾數條件下,振動減縮頻率的增大會減小尾渦的脫落頻率; Yu等[15]研究了前緣渦對翼型的升力阻力和力矩系數的影響,發現隨著減縮頻率k的增大,翼型的最大升力系數和相應迎角逐漸增大。Qin等[16]在低雷諾數情況下通過大渦模擬計算了不同減縮頻率下的SD7003翼型的氣動特性,發現減縮頻率k的增大會使升力系數隨時間變化(CL-t)曲線的相位變大;Yu和Bernal[17]發現在相同的減縮頻率情況下,振動軸位置的后移會延遲翼型周圍渦的發展,但是主要的流動結構并沒有改變。
而在小振幅振動研究中,目前所見的研究并不多,高正紅[13]在無黏跨聲速條件下,研究了振動軸位置和減縮頻率對小振幅振動翼型氣動特性的影響,研究發現小振幅簡諧振動翼型的升力系數-迎角(CL-α)曲線會呈現一個橢圓狀的環型曲線,指出減縮頻率的變大會使得CL-α曲線的繞向從逆時針變為順時針,而且當振動軸位置后移時,發生這種變向所對應的減縮頻率k值越大;Ekaterinaris和Platzer[18]利用面元法計算了NACA0012翼型的強迫振動,迎角幅度為±10°(未失速),發現翼型振動會帶來相位上的改變,而且減縮頻率k的增大會使得力矩系數遲滯環從逆時針變為順時針。
雖然已經有不少學者研究了翼型振動帶來的一些特殊現象,但是這其中仍有很多問題并沒有得到很好的解釋,目前大多學者都把遲滯環方向的改變簡單歸結為非定常效應引起的,張正秋等[19]指出,升力與扭矩的遲滯效應隨各參數的變化趨勢相同,但是從文獻[13]的計算結果可以看出,升力系數遲滯環的變化和力矩系數遲滯環的變化是不相同的,并且文獻[20]中指出“非失速情況下,氣動力系數的遲滯環面積表征了遲滯效應的大小”,注意到文獻[20]是在力矩系數變化情況下得到的結論,這一結論是否能推廣到升力系數遲滯環還有待研究。
可以看出目前專門針對翼型小振幅振動問題展開研究的并不是很多,而且多基于跨聲速情況,會有激波出現,對于低速情況,這種翼型小振幅振動會不會出現類似文獻[13]里的情況,有待研究。本文在前人的基礎上,結合本課題組在太陽能無人機實際飛行中遇到的特定問題,在低雷諾數條件下,從翼型小振幅振動入手研究振動軸位置和減縮頻率對振動翼型的氣動特性影響。
1 計算模型
本文采用的翼型為常用的低雷諾數翼型SD7037,網格劃分如圖1所示。Menter[21]指出,為準確地捕捉層流和轉捩邊界層,在低雷諾數流動計算中,需使y+接近于1。本文采用結構化的O型二維網格,翼型弦長為c,計算域邊界半徑為25c,整個計算域及壁面附近網格如圖1所示。
圖1 振動翼型的計算網格Fig.1 Calculation grid of oscillation airfoil
2 數值方法
當弦長雷諾數在2×105~1×106的范圍內變化時,基于雷諾時均的Navier-Stokes(RANS)方程也可以較好反映出翼型周圍的流場結構[18,22]。本文采用滑移網格方法實現翼型的振動,采用k-kl-ω轉捩模型,因為S-A(Spalart-Allmaras)及SST(Shear Stress Transport)k-ω湍流模型主要考慮的是全湍區域,很難預測低雷諾數下的分離泡結構,而k-kl-ω轉捩模型可以相對準確地捕捉觀察到翼型表面復雜流動現象及特征,轉捩位置及分離泡預測能力及精度相對較高,在低雷諾數轉捩流動數值求解中適用性較好[23]。
為了驗證本文所用轉捩模型的準確性,采用算例1的實驗數據[24],驗證了k-kl-ω轉捩模型捕捉低雷諾數分離泡特征的能力,結果如圖2所示(圖中Cp為壓力系數)。
算例1:翼型GA(W)-1,雷諾數Re=1.6×105,迎角α=12°。
本文中翼型的運動規律定義為
α=αmsin(ωt)
(1)
式中:αm為迎角運動幅度,本文中取為4°;ω為運動圓頻率,與減縮頻率k的關系為
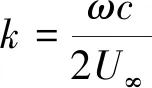
(2)
其中:U∞為來流速度。
為了加快收斂,本文先利用定常計算得到一個較為穩定的流場作為非定常運動計算的初始輸入,繼續進行非定常運動計算,每個時間步內的子迭代步數選為30,時間步長按無量綱時間t/T=0.004 5選取,其中T為翼型運動周期。
為了驗證本文采用的計算方法對非定常運動計算的可靠性,采用了2個算例來驗證。
算例2:利用Piziali[25]的實驗結果進行驗證,翼型為NACA0015,馬赫數Ma=0.29,Re=1.95×106,運動規律為α=4°+4.2°sin(2πft),其中頻率f=10 Hz。
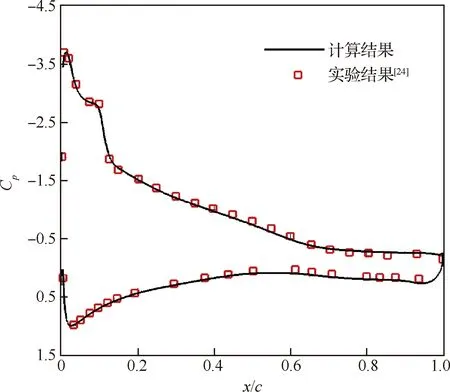
圖2 GA(W)-1翼型壓力分布(α=12°)Fig.2 Pressure distribution of GA (W)-1 airfoil (α=12°)
算例3:翼型為NACA0012,Re=485 755,Ma=0.035 5,運動規律為α=10°+10°sin(2πft),其中f=1.62 Hz,實驗條件及數據可以參考文獻[26]。
從圖3和圖4給出的升力系數遲滯環曲線中可以看出,本文采用的方法與實驗結果符合較好,說明本文采用的計算方法有足夠的可靠性。
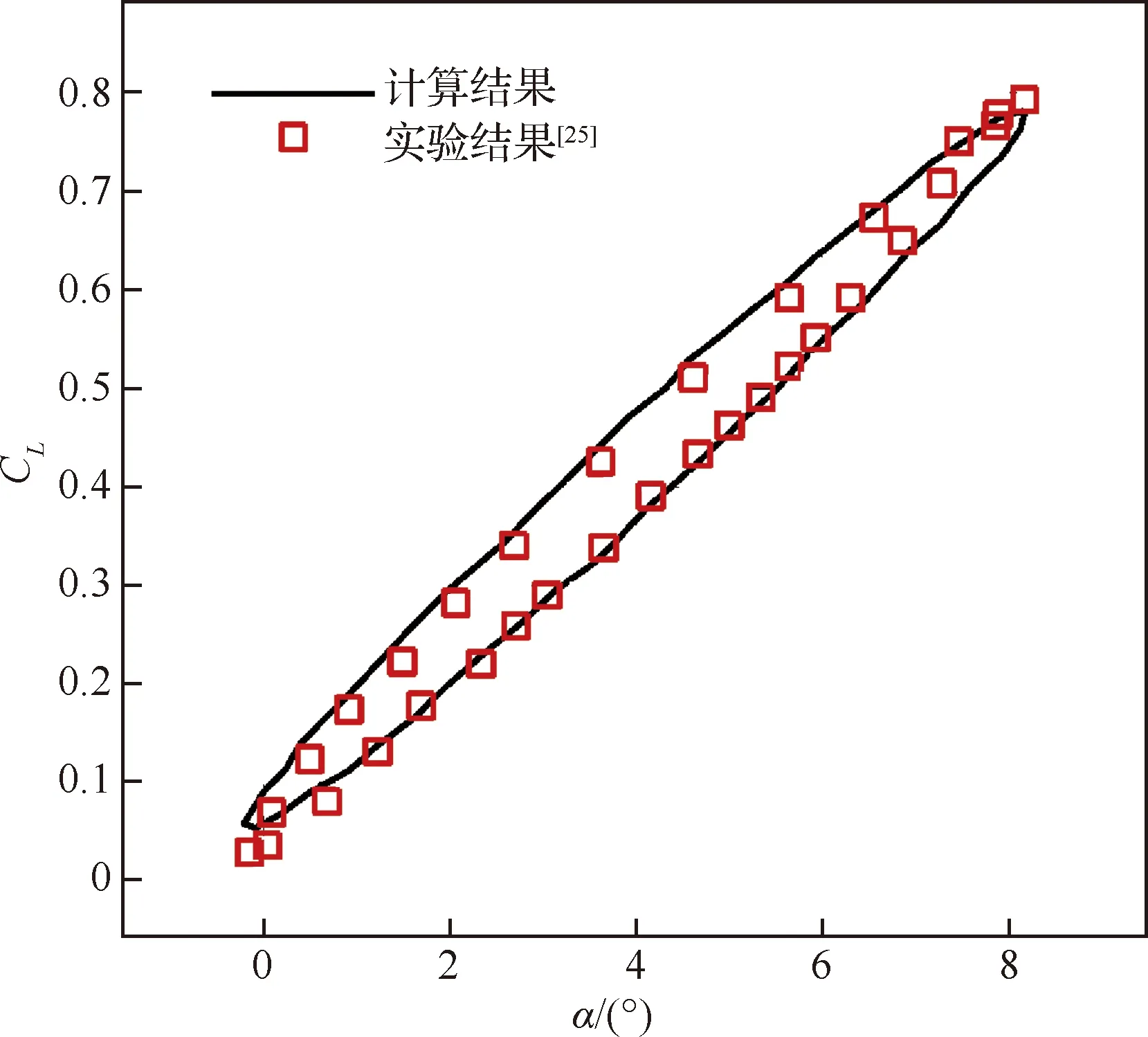
圖3 NACA0015翼型升力系數遲滯環Fig.3 Hysteresis loop of lift coefficient of NACA0015 airfoil
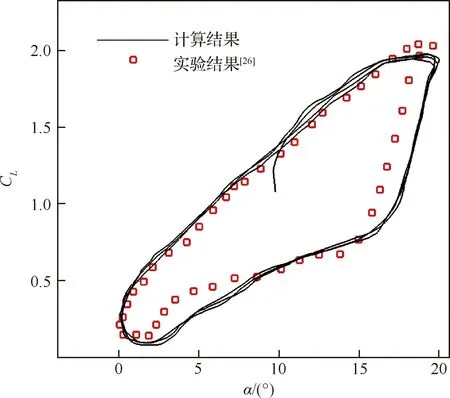
圖4 NACA0012翼型升力系數遲滯環Fig.4 Hysteresis loop of lift coefficient of NACA0012 airfoil
3 結果及討論
通過計算可以發現,當翼型作俯仰振動時,CL-α曲線呈現為一個橢圓形,而且方向上也有變化。為了研究振動軸位置和減縮頻率k對CL-α曲線遲滯環的繞向的影響,本文首先在減縮頻率不變的情況下,研究振動軸位置對遲滯環的影響,隨后通過更改減縮頻率k,研究k對遲滯環繞向的影響,并分析原因。
3.1 振動軸的影響
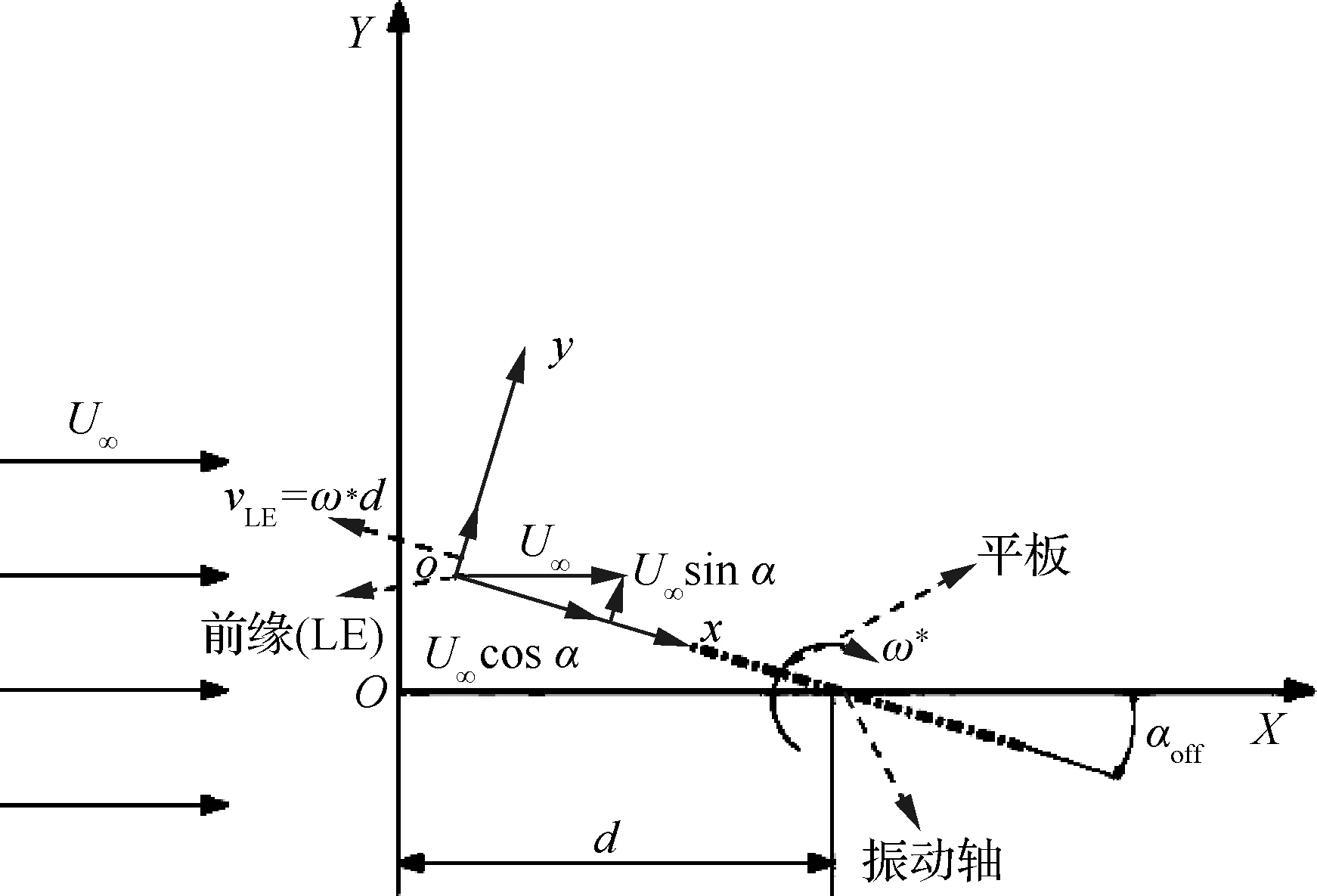
本文中定義了2個坐標系,一個是隨著平板運動的體坐標系oxy,另一個是固定的慣性系OXY(風軸系),當翼型未振動時,這2個坐標系是重合的,如圖5所示。分別將振動軸定位于前緣處、1/4弦線、半弦長、后緣處,即x=0,0.25c,0.50c,c處(見圖5)。
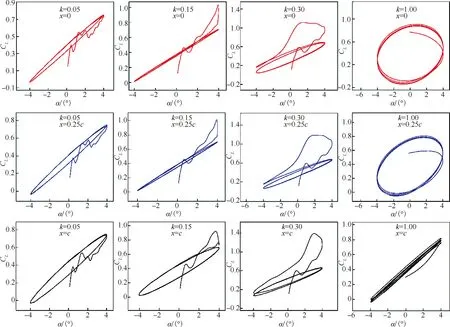
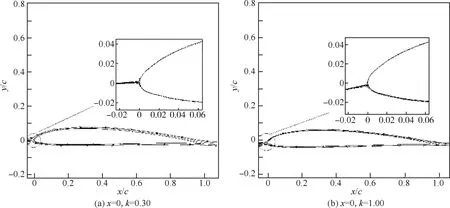
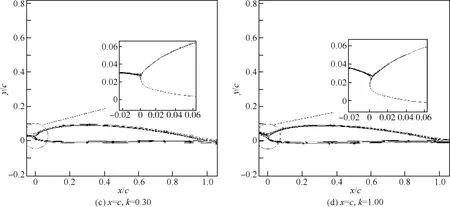
這里僅展現k=0.3和k=1.0時的計算結果分別如圖6和圖7所示。從圖6(a)可以看出,當k=0.3,翼型繞前緣轉動時,此時的CL-α曲線“遲滯環”的繞向為順時針,對比圖6(d)可以發現此時的“遲滯環”方向變為逆時針,即在k保持不變的情況下,當振動軸向后移動時,“遲滯環”方向有從順時針方向變為逆時針的趨勢,而且在這個變化過程中,會經歷一個“直線”過程,如圖6(c)所示。當k=1.0時,可以看出當振動軸從前緣移動到半弦長處時,對應的遲滯環均為順時針,但是當振動軸移動到后緣處時,CL-α曲線此時也出現了近似直線的情況,如圖7(d)所示。
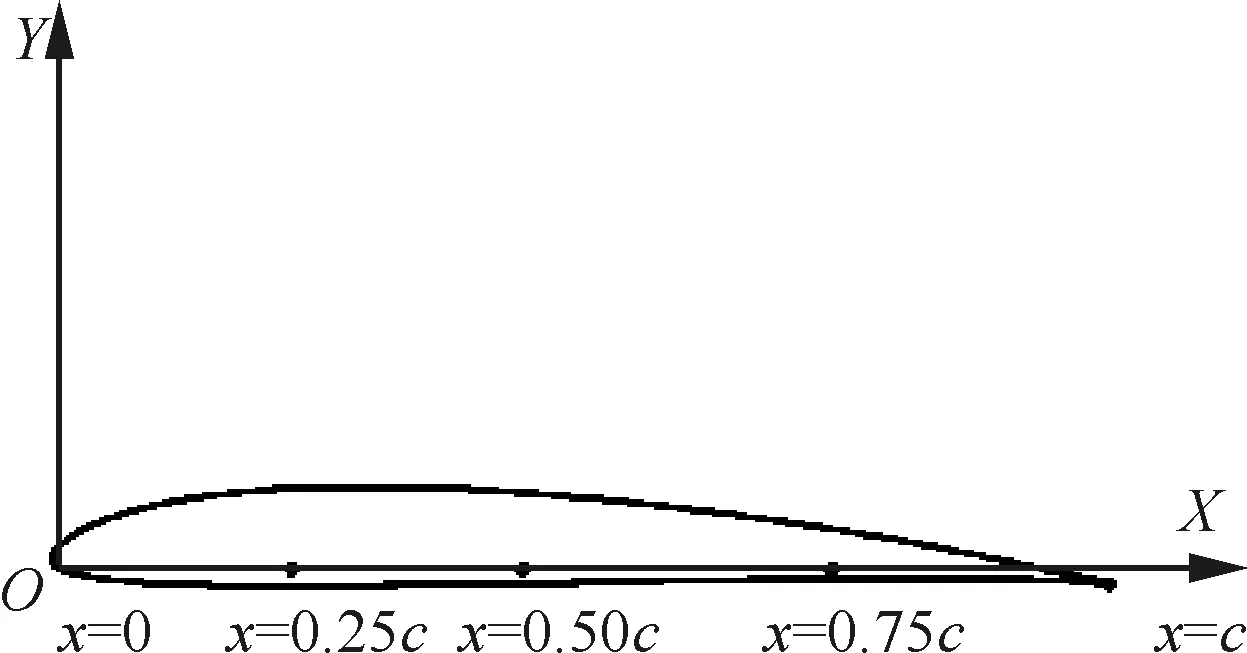
圖5 不同振動軸在坐標系中的示意圖Fig.5 Sketch of different pivot locations in coordinate system
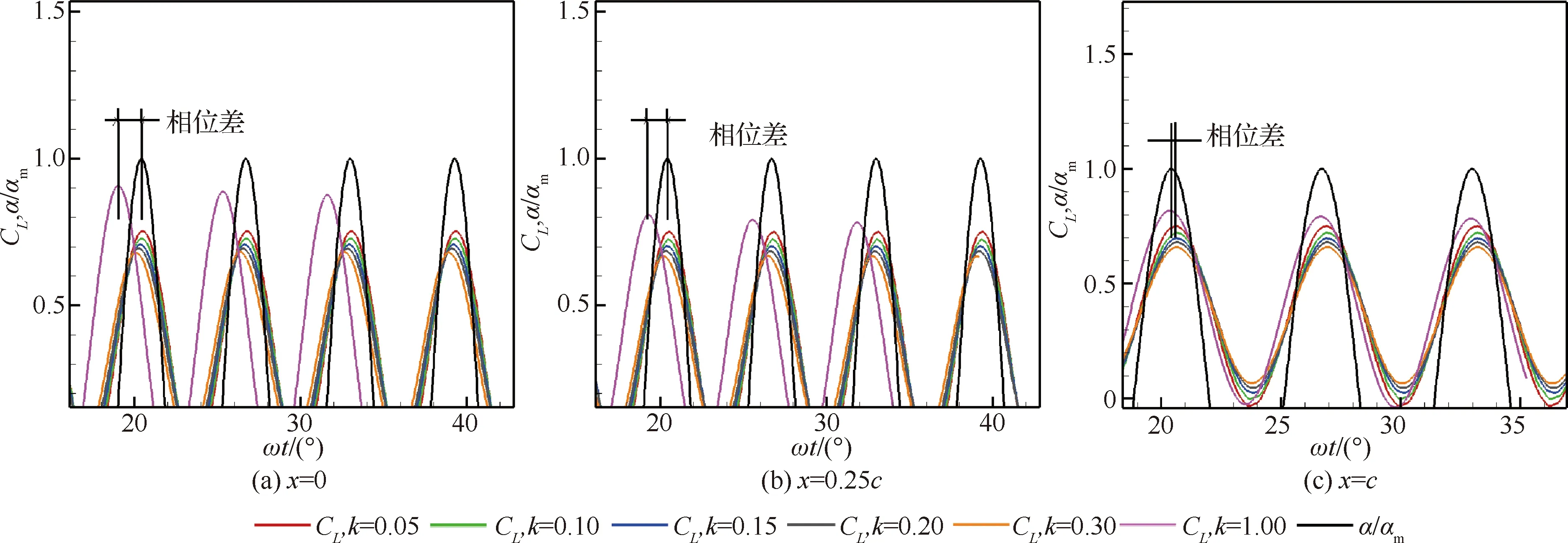
為了弄清楚這種現象的原因,將升力系數隨時間變化曲線展開,如圖8所示。從圖中可以看出k=0.3,振動軸位置從前緣向后移動時,升力系數的峰(谷)值在時間上均出現了向后移動。
表1給出了不同雷諾數下對應不同振動位置的升力系數曲線特性,表1中的Δt和φ是相對于α-t曲線計算得到的時間差和相位差,負值代表相位相對α-t曲線(時間)延遲,正值代表相位提前;CLmax和CLmin分別為升力系數的最大值和最小值,CLamp為振動時升力系數的幅值大小,CLmean為
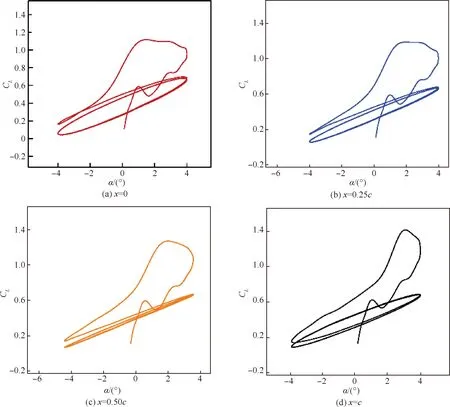
圖6 k=0.3時不同振動位置的CL-α曲線(Re=7.89×105)Fig.6 CL-α curves at different pivot locations at k=0.3 (Re=7.89×105)
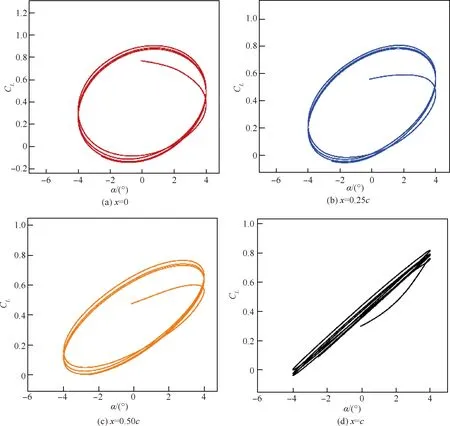
圖7 k=1.0時不同振動位置的CL-α曲線(Re=7.89×105)Fig.7 CL-α curves at different pivot locations at k=1.0 (Re=7.89×105)
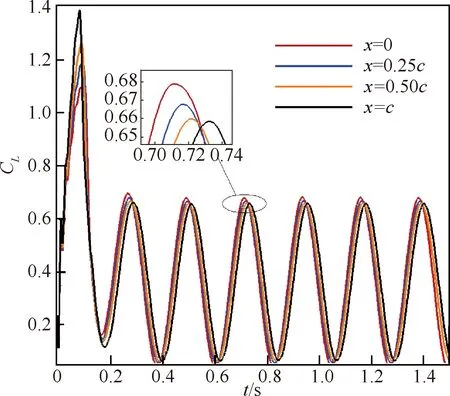
圖8 k=0.3時不同振動位置的CL-t曲線(Re=7.89×105)Fig.8 CL-t curves at different pivot locations at k=0.3 (Re=7.89×105)
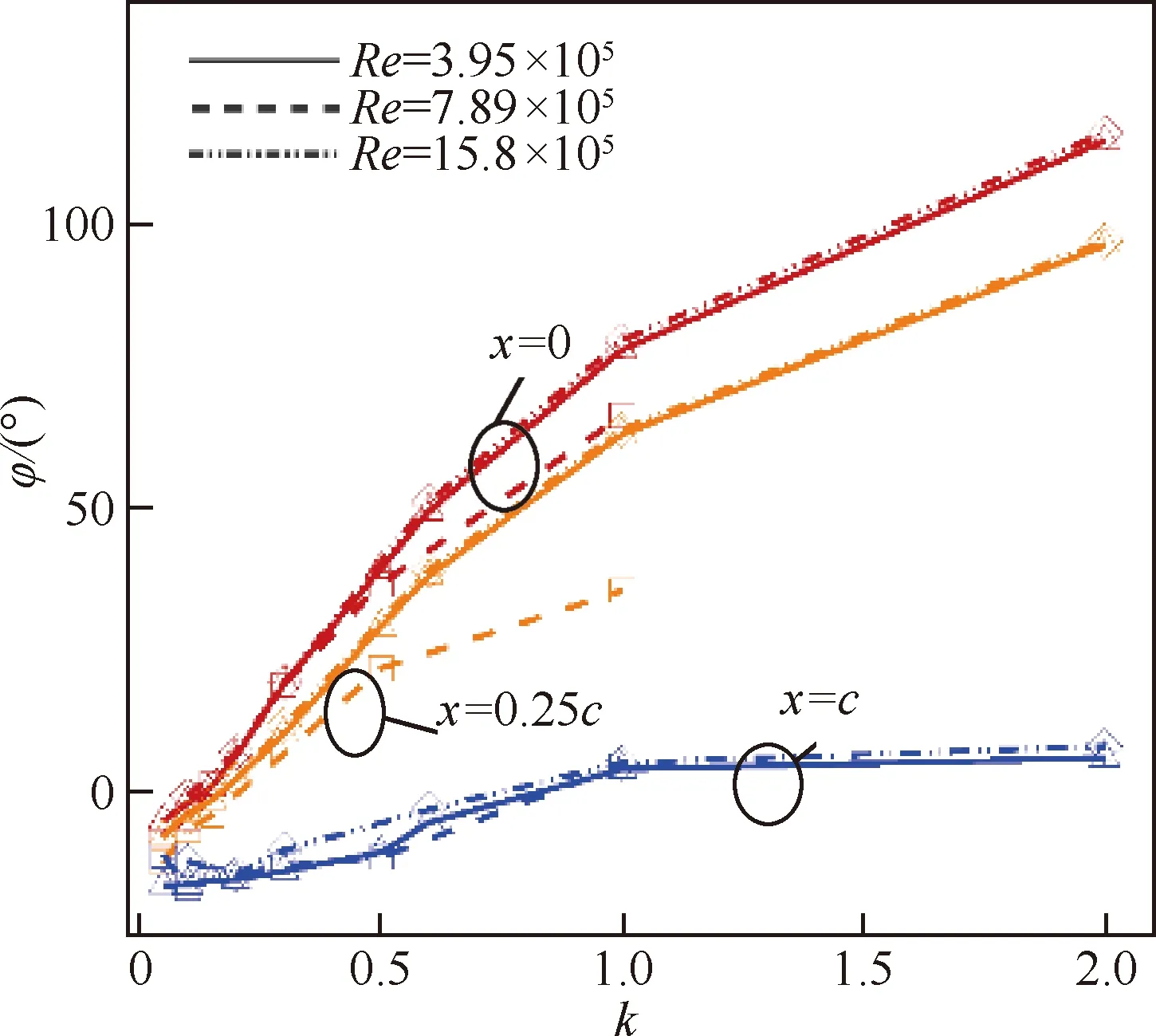
升力系數的平均值。從表1中可以看出,振動軸的位置對升力的平均值影響不大,而且振動軸的位置越靠近后緣,升力系數能達到的最大值越小;對于同一振動軸位置,隨著雷諾數的變大,時間和相位在數值上是逐漸增大的,雖然對于x=c位置來說,相位為負值,代表此時CL-t曲線相對于α-t曲線相位滯后,但是隨著雷諾數的增大,其滯后相位的絕對值也在變小,即當雷諾數變大時,會使得相位提前變多。
此外,從表1中還可以看出Re=7.89×105時,x=0位置處的相位較迎角曲線的相位要提前19.22°,x=0.25c位置相位提前10.43°,而對于x=c位置,相位滯后11.52°,這種相位上的差別就導致了遲滯環曲線的方向變化,這里可以從數學上加以證明。
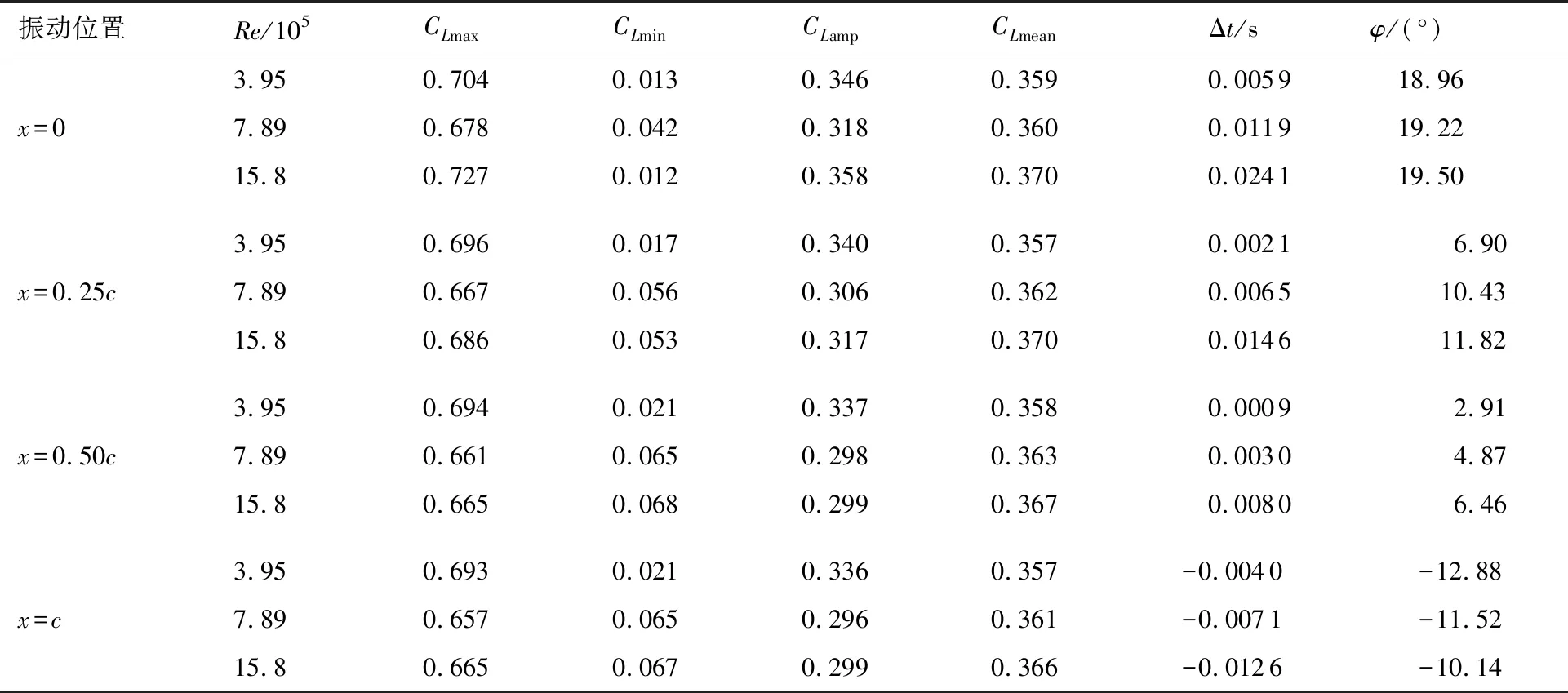
表1 不同雷諾數下對應不同振動位置的升力系數曲線特性(k=0.3)
迎角的運動形式為α(t)=αmsin(ωt),穩定后的升力系數曲線可以寫為:CL(t)=CLampsin(ωt+φ),這點在3.2節可以被證明。
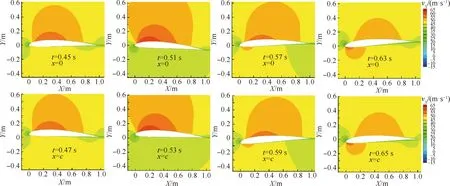
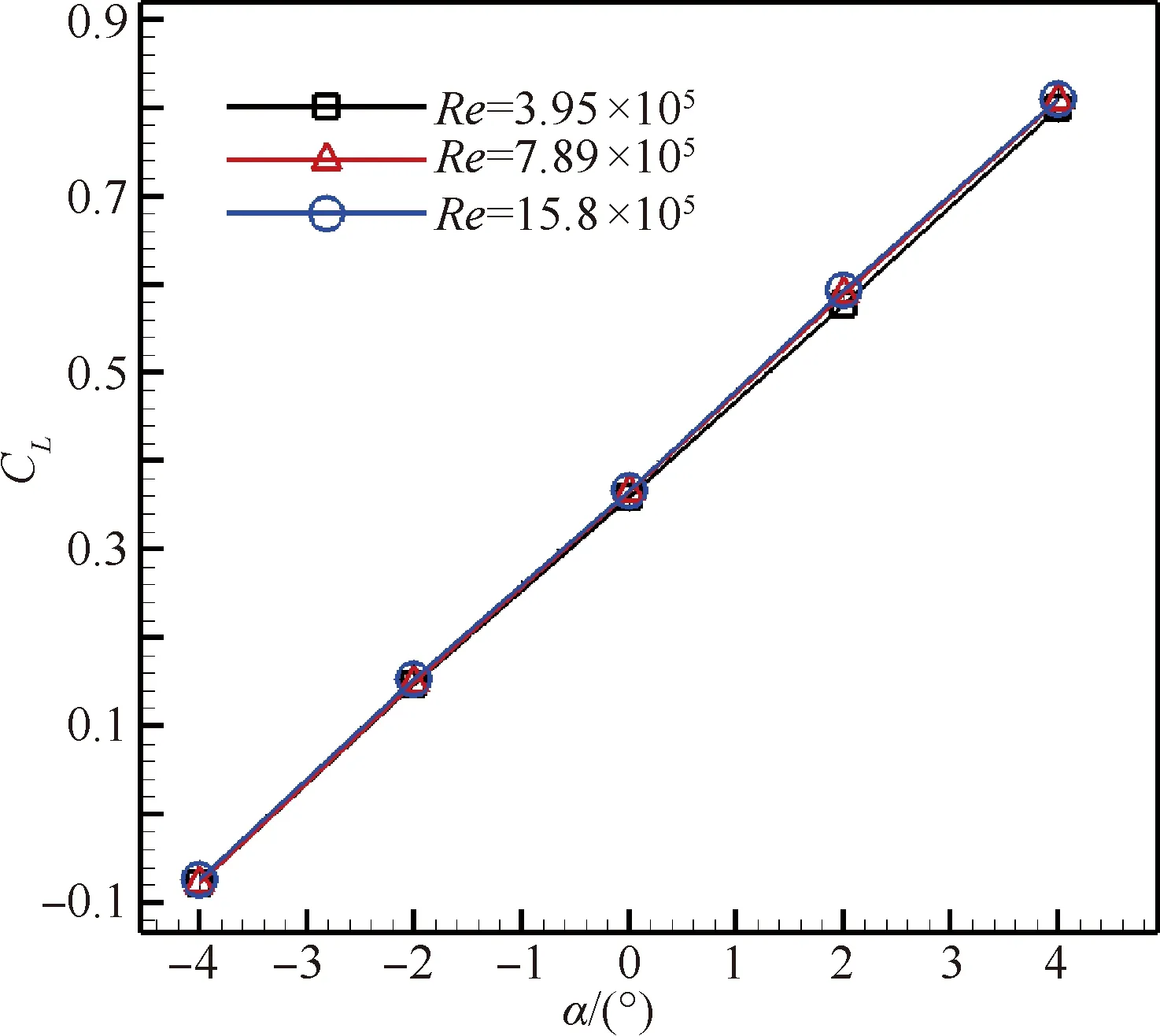
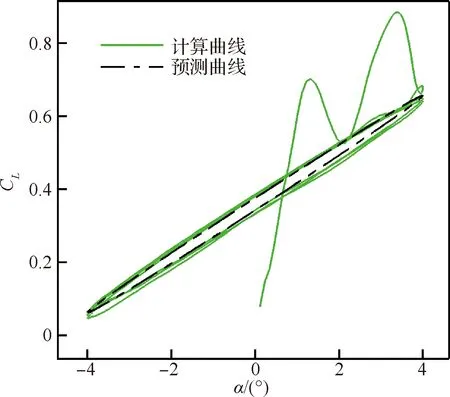
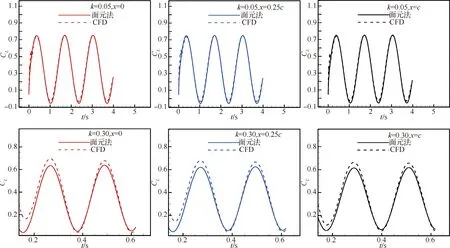
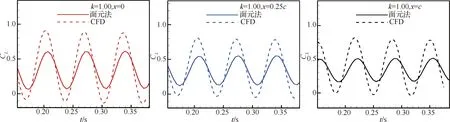
為了方便說明,以前1/4周期為例(其他情況類似),t1(t1 從數學關系上的證明可以看出,在一定范圍內,相位φ的絕對值越大,t1、t2時刻對應的升力系數差別越大,即遲滯環表現得會更加飽滿(無論是順時針還是逆時針),而φ又與振動軸位置和k相關,所以這才是導致遲滯環變化的根本原因,而不是簡單的增大k就會導致遲滯環飽滿,對比圖7(d)和圖6(d),可以看出增大k也可能使得遲滯環曲線變得扁平,甚至為直線;從圖6和圖7中還可以看出,向前移動振動軸位置也可能使得遲滯環變得更加飽滿。 圖9 相位差φ帶來的升力系數差Fig.9 Lift coefficient difference caused by phase difference φ 從以上分析可以看出,當振動軸位置向后緣移動時,CL-t曲線的相位會變小,即出現相位延遲,CL-α曲線也會從順時針向逆時針變化。對于此現象,可以有如下解釋:以平板為例,振動軸位置定在離前緣d處,如圖10所示。假設整個平板在來流速度為U∞的流場里以ω*的角速度繞振動軸順時針旋轉(即迎角增大),則在體軸系里面觀察,前緣處會有一個vLE=ω*d的向上速度,如圖10所示,而當迎角為αoff時,此時在體軸系里觀察來流,在y方向上的速度為vy=U∞sinαoff,但是注意到此時前緣自身仍有一個vLE的向上速度,所以前緣處感受到的實際速度只有vLE-real=U∞sinαoff-vLE,也就是說實際迎角被減小了,而且只有當αoff=arcsin(ω*d/U∞)≈ω*d/U∞(小角度)才能剛好抵消前緣運動速度的影響,此時在體軸系觀察,來流沿x方向流過,迎角為0°,即相比較繞前緣振動,時間上滯后了。 這里雖然只對前緣處作了分析,但是其他位置處的有效迎角是相似的,在振動軸前的部分有效迎角是減小的,振動軸后處的部分有效迎角在增大,這也可以看出當d較大時,即振動軸離前緣的位置越遠,有效迎角減小的部分更多,要達到和繞前緣振動相同狀態則需要更長的時間,反映在升力系數上,就是振動軸的后移延遲了相位,如圖8所示。此外,還可以看出振動軸帶來的相位滯后在k一定的情況下,主要和離前緣的距離d和當地的平均流速Uav的比值近似呈線性關系。 圖11中展現了翼型振動時沿X方向的速度vX云圖,從圖11中可以看出,當振動軸位于翼型后緣(x=c)時,基本上要比繞前緣處(x=0)振動滯后0.02 s,才會出現相似的流場結構。 圖10 平板的速度示意圖Fig.10 Sketch of velocity of flat plate 圖11 繞前緣和后緣振動不同時刻的vX云圖對比(k=0.3)Fig.11 Comparison of vX contour at different times when pivot located at leading edge and trailing edge (k=0.3) 本節在相同振動軸位置,研究了不同k對遲滯環曲線的影響。圖12給出了x=0,0.25c,c時,k=0.05,0.15,0.30,1.00的計算結果。 從圖12中可以看到,在不同振動軸處,隨著k的變大,“遲滯環”的轉向會從逆時針向順時針轉變,中間會出現直線段過程,這并不如文獻[19]結論中指出的那樣,“隨著振動頻率的增加,氣動力系數遲滯曲線飽滿程度增加”。可以看出增大k值類似于振動軸的前移過程,也可以提前相位。 從圖12中還可以看出,當k=1.00時,越靠近前緣處,升力系數遲滯環面積越大,這主要是因為當振動軸靠近前緣時,初始的負相位φ的絕對值較小,因此k增大到一個較小的值時,就會抵消這個負相位,此時升力系數遲滯環即變為直線型,繼續增大k這個相位φ就會變成正值,并不斷變大,按3.1節的解釋,遲滯環面積會變大,且此時的升力系數遲滯環為順時針轉向,而當振動軸位置靠近后緣時,這個初始的滯后相位的絕對值會較大,因此k需要增大到更大的水平才能抵消這個滯后相位,所以反映到遲滯環曲線上,如圖12,當k=1.00時,越靠近前緣的振動軸位置的曲線更加飽滿,當振動軸位于后緣時,CL-α曲線基本呈直線型,表明當振動軸位于后緣時,當k增大到1.00時,才能抵消相位滯后,而當振動軸位于前緣時,k只需到0.15,就可以抵消相位的滯后了。 圖13將不同k下的CL-t曲線與α-t曲線進行了對比,可以看出,隨著k的變大,CL-t曲線相對于此時對應的α-t曲線的相位逐漸變大,即k的增大可以使得相位提前,此時對應的CL-α曲線遲滯環也會從逆時針向順時針變化,直線段則對應相位差為0°的情況。 圖12 不同振動軸位置隨k變化的CL-α曲線(Re=7.89×105)Fig.12 Variation of CL-α curves with k at different pivot locations (Re=7.89×105) 圖13 不同k的CL-t曲線與α-t曲線的對比(Re=7.89×105)Fig.13 Comparison between CL-t curves and α-t curves for different k (Re=7.89×105) 圖14給出了φ隨k的變化,可以清楚地看到對于同一振動軸,k的增大使得曲線的相位提前,而且曲線的相位是與減縮頻率k和振動軸有關的,此外可以看出相位與k之間存在一個函數關系,這點也在后文中進行了證明。 圖15給出了SD7037翼型在不同雷諾數下的小迎角升力系數曲線,可以看出在氣動上,本文選取的翼型在小迎角范圍內,升力系數和迎角近似呈線性關系CL=CLαα(CLα為升力線斜率),現在將翼型及流場之間的共同作用看成一個系統,升力系數是輸出量,很明顯在小迎角范圍內此時這個系統滿足線性系統的定義,本質上是線性的。從控制的角度來看,一個系統的線性與否是其自身屬性,與輸入量沒有關系,雖然這里的輸入為迎角的變化:α=αmsin(ωt),但是不會改變這個系統的線性特點,所以本文在這里將此系統看作是線性系統。另外從圖8中也可以看出,升力系數CL此時也是正弦變化形式,而且頻率保持與迎角變化頻率一致,也從側面驗證了這種假設的合理性。在線性系統假設的前提下,輸入(迎角)和輸出(升力系數、力矩系數)的關系可證明如下。 圖14 CL-t曲線與α-t曲線之間的相位差φ隨k的變化Fig.14 Variation of phase shift φ between CL-t curve and α-t curve with k 圖15 SD7037翼型在不同雷諾數下的小迎角升力系數曲線Fig.15 Lift coefficient curves of SD7037 airfoil at small angles of attack with different Reynolds numbers 系統的輸入為α(t)=αmsin(ωt),則輸出的拉氏變換可以寫為 CL(s)=Φ(s)αm(s) (3) 式中: Φ(s)為整個系統的傳遞函數;M(s)為Φ(s)的分子多項式;-s1,-s2,…,-sn為系統極點。為了方便討論,不妨認為系統穩定,并假設特征根均為互異的負實根,利用部分分式展開法即有: (4) A2e-s2t+…+Ane-snt (5) 當t趨于無窮時,輸出穩態分量: (6) 所以穩態分量為 CL(t)|t→∞=αm|Φ(jω)|· αm|Φ(jω)|sin(ωt+∠Φ(jω))= CLamp(ω)sin(ωt+φ(ω)) (7) 從證明中可以看出,振幅CLamp和相位φ都是與ω有關的函數,這也驗證了圖14所示的規律。 結合以上證明,如果小振幅振動的翼型可以被看成一個線性系統,則可做一個合理的假設,即當雷諾數和振動軸位置確定后,運動的初始相位不會影響最終的CL-t曲線的相位。為了驗證這一假設,本文選取k=0.30、振動軸位置為x=0.25c和x=c處進行分析,從表1可以看出,振動軸位于0.25c處時,CL-t曲線相對α-t曲線的相位本身就是提前的,而振動軸位于后緣時,這個相位是負值,即相位滯后了。為了驗證初始相位對最終CL-t曲線相位的影響,在x=0.25c處預加-18°的初始相位,即α=αmsin(ωt-18°),相應的在x=c處預加+18°的初始相位,即α=αmsin(ωt+18°)。計算結果如表2所示,對比表1中的數據,可以發現初始相位的存在并沒有改變最終的相位特性,即CL-t曲線的相位不受迎角的初始相位影響。 表2 改變初始相位后的CL-t曲線相位特性 Table 2 Phase characteristics ofCL-tcurve after changing initial phase 在3.1節的分析中,已清楚了振動軸位置主要是通過影響有效迎角進而影響相位的變化,接下來研究k的變化對相位的影響。 注意到本文研究的是翼型的簡諧強迫振動,所以這里參考了二維Theodorsen非定常氣動力模型,具體表達式[27-28]為 將本文的翼型運動規律帶入化簡,可以得到升力系數表達式: CL=πkαm(cos(ωt)+aksin(ωt))+…+ (9) 參考文獻[17,29],本文在這里把翼型排開空氣的質量稱為“附加質量”,而且文獻[17,29]的研究結果都指出:“當k較大時,翼型排開的空氣質量帶來的慣性反作用力會帶來額外的升力,從而提前相位”,而且可以看出當k較大時,帶來的額外升力也會比較明顯。 從式(9)中還可以看出,這個附加質量帶來的慣性反作用力只會對升力的幅值和相位有所影響,并不影響CL-t曲線的頻率特性,這與計算結果也是相符合的。 此外,從圖14中可以看出,當振動軸位置向后緣移動時,k增大帶來的相位增加并不明顯,即升力系數曲線的相位對k不再敏感了,這與文獻[13] 的結論相似,從本節的分析可以看出,當k變大時,翼型排開的附加質量帶來的慣性反作用力會變大,使得翼型升力變大。從式(9)可以得到在周期開始時(瞬時迎角為0°),由于反作用力帶來的升力系數增量為ΔCL=πkαm,所以當k=1.00 時,由于反作用力帶來的升力系數增量ΔCL1-t=0.219 3,k=0.30時,升力系數增量ΔCL2-t=0.065 8,即k=1.00相比于k=0.30,升力系數差值為ΔCL-t=0.153 5,從圖13中可以得到繞前緣振動時,k=1.00和k=0.30在周期開始時升力系數差值為ΔCL1-c=0.221 1,而繞后緣振動時,對應的升力系數差值ΔCL2-c=0.116 6,此時有ΔCL1-c>ΔCL-t>ΔCL2-c,可以看出當振動軸后移時,升力增量的確是減小的,這主要是因為當振動軸在前緣時,翼型在迎角增大的過程中,有效迎角也在變大,如圖16(a)和圖16(b)所示,即此時升力的2個組成部分,附加質量帶來的反作用力和常規的氣動力都是增加的,因此相位提前很顯著,而當振動軸后移時,特別地,對于振動軸在后緣時,翼型上的有效迎角是減小的,如圖16(c)和圖16(d) 所示,雖然由于附加質量帶來的反作用力隨k的增大在增大,但是翼型上產生的氣動力由于有效迎角的變小在減少,而且振動軸后移本身會帶來負相位,這就大大抵消了慣性力帶來的額外升力增量,表現出來的就是k增大,相位增加緩慢。 圖16 繞前緣和后緣振動時翼型周圍流場隨k的變化(Re=7.89×105)Fig.16 Variations of flow field around airfoil with k when pivot located at leading edge and trailing edge (Re=7.89×105) 從3.1節和3.2節的分析可知,利用已知的計算結果得到繞其他振動軸位置振動的升力系數曲線(幅值會略有差別)是可行的,例如,當k=0.30,Re=7.89×105時,從表1可以看出,繞x=0.50c處振動時CL-t曲線的相位偏移為4.87°,即時間上提前0.003 s,而繞x=c處振動時,相位和時間分別為-11.52°和-0.007 1 s(負號代表滯后),根據本文的結論,在這兩個振動軸位置之間必然會出現相位為0的情況,即CL-α曲線呈現直線型,而且可以根據這兩個狀態推算出相位為0°時對應的振動軸位置。首先,從這兩個狀態可以推算出x=0.50c到后緣處這一段翼型表面的平均流動速度為 Uav=(c-0.5c)/(0.003+0.007 1)=49.5cm/s 假設振動軸位置位于x0處時,相位差為0°,即時間差也為0,從3.1節的分析可以看出振動軸位置對相位的影響主要是線性的,所以有 x0-0.5c=Uav×0.003≈0.15c 即這個振動軸位置位于x=0.65c時,CL-α曲線近似呈現直線型。 圖17 k=0.30,x=0.65c時的CL-α曲線(Re=7.89×105)Fig.17 CL-α curve at k=0.30, x=0.65c (Re=7.89×105) k=0.30,x=0.65c時的CL-α曲線如圖17所示,驗證了推算的準確性。相應地,如果想推算已知振動軸位置的升力系數曲線,可以利用同樣的方法,推算出此振動位置的CL-t曲線與α-t曲線的相位差,如當k=0.30時,已知振動軸位置x=0.75c,利用x=0.50c和x=c的結果可以推算出其時間上滯后0.002 s,即相位差應為-3.23°,則升力系數曲線為 CL-x=0.75c=CLmean+CLampsin(ωt-3.23°) (10) 式中:CLmean和CLamp可以由表1插值得到,這里分別為0.362和0.297。 如圖18所示,推算的結果和計算的結果符合良好,可以看出本文得出的結論是正確可靠的,這對于工程實際應用有較大的意義,例如可以通過計算或實驗獲得容易測量位置的結果,以此推算出其他位置的結果。 此外,根據本文的分析,小振幅振動的翼型并沒有牽涉到渦的形成和發展,這也意味著傳統的勢流理論一定程度上也可以預測這種遲滯環變向的現象。 圖18 k=0.30, x=0.75c時的預測曲線和計算曲線對比Fig.18 Comparison between predicted curve and calculated curve at k=0.30, x=0.75c 本文利用面元法[30]計算了相應的狀態,結果如圖19所示,可以看出當k<0.30時,面元法預測的結果和基于RANS方程計算的結果高度一致,但是當k=1.00時,升力系數計算結果不僅在幅值上有較大差別,而且相位預測也有差異。這主要是因為傳統的勢流理論只能處理附著流,而從圖16中可以看出,當k增大到一定程度時,振動翼型周圍流場特別是前緣處的有效迎角被改變,因此面元法計算結果也和CFD結果相差較大。但是,面元法在一定程度上還是提供了一種更加快速的研究小振幅振動翼型氣動特性的方法。 圖19 面元法與CFD動網格計算結果對比(Re=7.89×105)Fig.19 Comparison of calculated results of panel method and CFD sliding mesh (Re=7.89×105) 1) 遲滯環現象主要是升力系數、力矩系數隨時間變化的曲線在相位上與迎角變化規律曲線的差異,當升力系數曲線與迎角隨時間變化曲線的相位差φ>0°,即升力曲線相位提前時,升力系數隨迎角變化的遲滯環曲線呈現順時針變化規律,而當φ<0°,即升力曲線相位滯后時,遲滯環曲線呈現逆時針變化,當φ=0°時,此時的升力曲線恰好為直線型,而這個相位與振動軸位置和減縮頻率k有著密切關系。 2) 振動軸的影響:本文的計算結果顯示,振動軸位置后移會帶來相位上的延遲,而且這種影響近似呈線性關系。相位上的延遲,使得遲滯環向順時針變化就越困難,即相同的k下,振動軸的位置越靠后,升力系數遲滯環越可能呈現逆時針變化。 3) 減縮頻率k的影響:減縮頻率k對升力系數曲線的影響機制與振動軸不同,k的增大,帶動周圍空氣振動從而帶來的慣性反作用力增大,進而提高了升力,即提前了相位,但是并不改變CL-t曲線的頻率。可以看出這種變化不再類似振動軸位置的線性影響。 4) 雷諾數的影響:本文研究結果表明,當雷諾數變大時,流動黏性會相對變弱,因此相位滯后比低雷諾數時較小,但是不會使得遲滯環現象消失,文獻[13]在無黏情況下(可以看成雷諾數無窮大)也觀察到了遲滯環現象,與本文結論類似。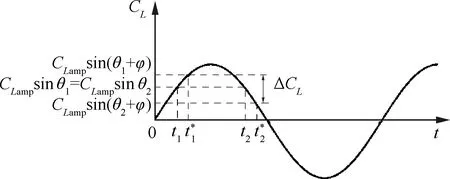
3.2 減縮頻率的影響
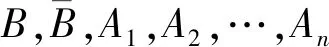

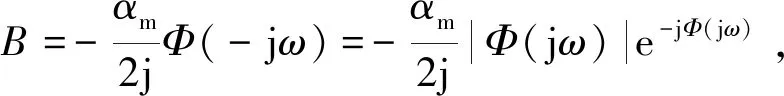
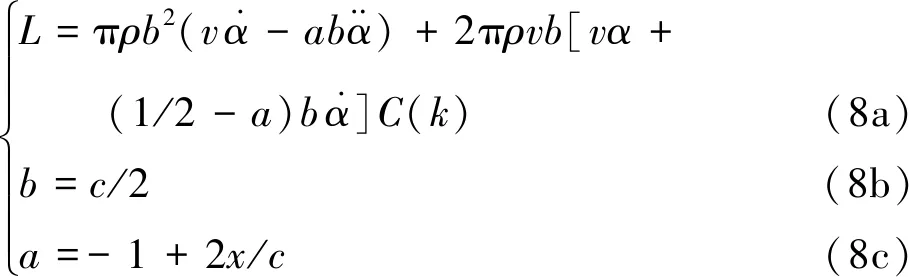
3.3 推論及應用
4 結 論

