模擬退火算法在物流線路選擇方面的研究

楊飛

摘要：隨著電子商務的不斷發展，互聯網訂單數量的不斷增加，線下物流配送的壓力越來越大。如何設計一個效果優良，可靠性強的物流線路選擇方法越來越成為人們關注的熱點。文章采用模擬退火算法對多節點物流配送路線最短選擇問題進行了研究，建立了適用于物流配送路線最短問題的模擬退火算法方法。對于物流配送最短路線的優化計算提供了算法參考。對于其他行業關于多節點遍歷路線最短問題同樣具有參考意義。

關鍵詞：模擬退火算法；物流配送；線路選擇

中圖分類號：TP301.6 文獻標識碼：A 文章編號：1009-3044（2019）04-0270-02

隨著電子商務的不斷發展，互聯網訂單數量的不斷增加，線下物流配送的壓力越來越大。在此背景下，現有諸多電商和物流相關企業都在進行物流配送線路選擇的研究和應用，如阿里巴巴，京東等。物流配送研究是為了解決物流線路規劃的問題而存在的，其是一個典型的旅行商問題[1]（Travelling Salesman Problem，TSP），它是一個組合優化問題。關于物流線路選擇問題，可以將每個城市看成一個AOV有向圖的節點，節點與節點之間有的單向連接，有的雙向連接，也有的沒有連接。如圖1所示。

從圖1中選擇任意一個節點作為開始節點，找出一條路徑，路徑包含剩余所有節點，并只包含一次，最后返回到開始節點，要求這條路徑所花費的代價最少（距離最短），這就是TSP問題。物流線路選擇作為一個典型的TSP問題，當城市個數增加時，它可能的配送路線數量是成指數型增長的，是一個NP[2]難題。眾所周知，NP難問題是很難精確的求出其最優解，因此，對于物流線路選擇問題求出近似解是具有意義的。

1 相關工作

目前，在電商行業和物流行業飛速發展的背景下，關于物流配送的路徑規劃方面的研究越來越多。劉婷婷等人根據物流配送最短路線規劃的現狀，利用最小生成樹法對現有問題進行分析，通過資料整合、建立實例模型、使用Kruskal算法建立模型、比較權值大小并用canvas畫布顯示最終路徑圖形等過程，得出物流配送網絡的最佳路徑，最后用Java實現整個模型，得出最短路徑和最低時耗方案[3]。張倩等人針對 如何更好地確保電商平臺生鮮食品冷鏈物流運作成本和運作效率的問題，提出了一種改進的蟻群算法，優化了生鮮電商冷鏈物流的配送路徑，并通過實例仿真驗證了優化方法的可行性[4]。王勇等人采用遺傳算法對多節點物流配送路線最短選擇問題進行了研究，建立了適用于物流配送路線最短問題的遺傳算法方法[5]。

此外，由于物流配送的路徑規劃本質就是TSP問題的研究，所以關于TSP問題的研究工作是在研究物流配送的路徑規劃問題時不可避免的。李陽等人為優化TSP，結合禁忌搜索算法（TS）和模擬退火算法（SA）的思想設計了混合退火算法（TSA）。針對模擬退火算法搜索效果不穩定等問題，在初始階段TSA多次禁忌搜索并篩選初始解，確保算法穩定地收斂到全局最優值，在求解部分設計了快速退火算法，使其快速退火并收斂。與其他算法相比，TSA求解精度高，求解效果穩定魯棒性強，并且求解時間短[6]。Christine等人提出了一種進化分裂與侵占（EDAC）方法，用于替代遺傳算法在硬組合搜索中的應用，該方法可以利用對子問題的良好解決方案的知識來改進問題本身的解決方案。文中使用遺傳算法來探索問題細分的空間，而不是解決方案本身的空間，并給出了應用于幾何TSP的該方法的一些初步結果[7]。

2 模擬退火算法原理

SA起源于物理學中固體退火原理，固體退火過程包括加溫過程、等溫過程和冷卻過程。固體加溫過程中，固體內部粒子隨著溫度的上升變成了無序狀，導致內能增大。固體等溫過程中，固體內部粒子漸趨有序，致使在每個溫度都達到平衡態。固體冷卻過程中，固體內部粒子隨著冷卻達到基態，內能減小為最小。模擬退火法的一般原理如下：

1）初始溫度為[T0]，及初始點[x]，計算該點的函數值[f（x）]；

2）隨機產生擾動[?x]，得出新點[x'=x+?x]，計算新點函數值[f（x'）]，和函數值差[?f=fx'=f（x）]；

3）假如[?f≤0]，則接受新點，當做下一次模擬的初始點；

4）假如[?f>0]，則計算新點接受概率：[p?f=exp -?fK?T]，產生[0，1]區間上均勻分布的偽隨機數[r]，[r∈0，1]，若[p（?f）≥r]，則接受新點作為下一次模擬的初始點；否則放棄新點，仍取原來的點作為下一次模擬的初始點。

以上的原理過程也稱為Metropolis過程。可遵循一定的物理退火原理逐步降低物體溫度，重復Metropolis過程，形成模擬退火算法。

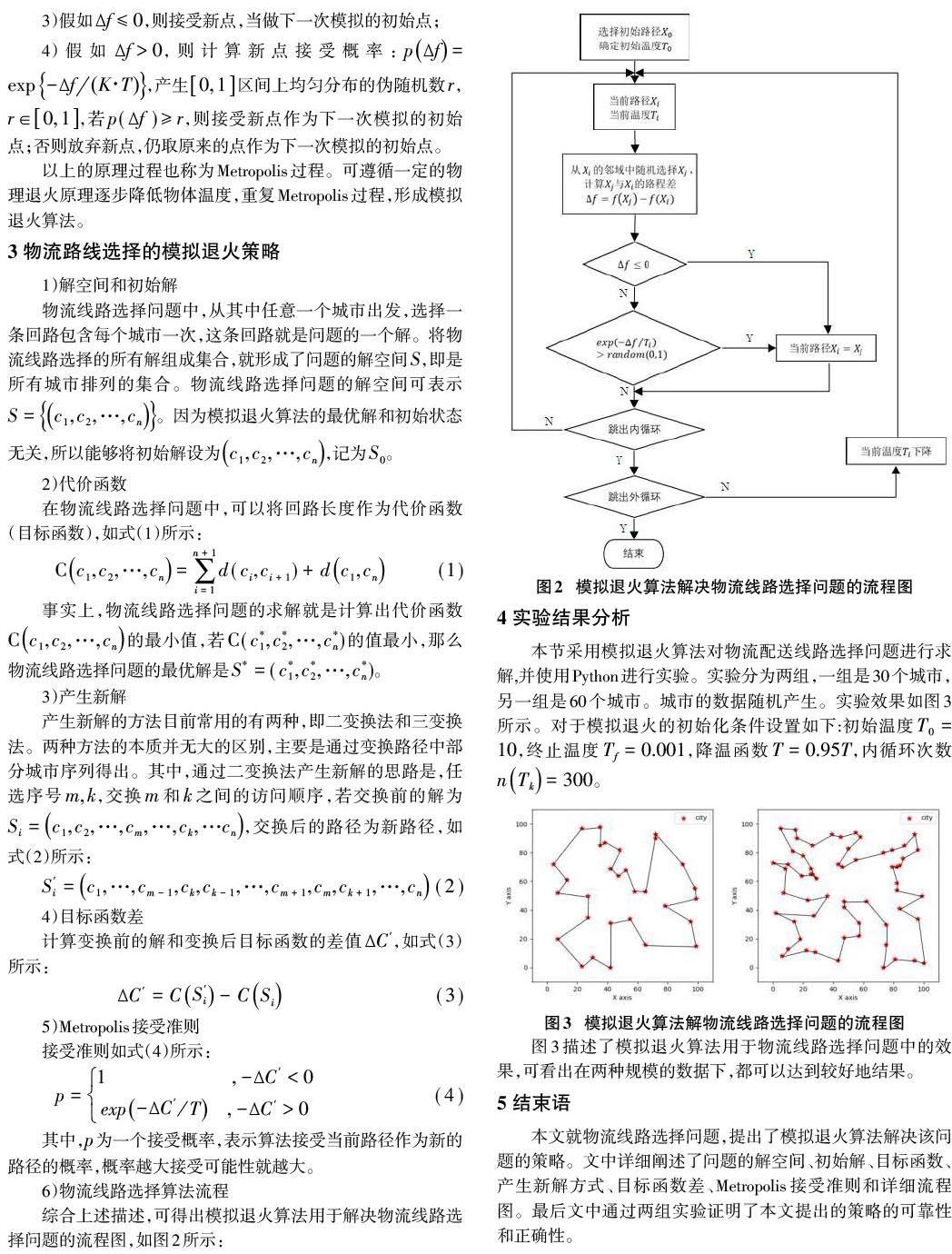
3 物流路線選擇的模擬退火策略

1）解空間和初始解

5 結束語

本文就物流線路選擇問題，提出了模擬退火算法解決該問題的策略。文中詳細闡述了問題的解空間、初始解、目標函數、產生新解方式、目標函數差、Metropolis接受準則和詳細流程圖。最后文中通過兩組實驗證明了本文提出的策略的可靠性和正確性。

參考文獻：

[1] Tao G， Michalewicz Z. Inver-over Operator for the TSP： International Conference on Parallel Problem Solving from Nature[C]， 1998.

[2] Woeginger G J. Exact Algorithms for NP-Hard Problems： A Survey[J]. 2003.

[3] 劉婷婷， 于衛紅. 物流配送網絡最短路線規劃[J]. 電子商務， 2018（12）：9-10.

[4] 張倩， 張悟移， Rattapon Incharroen. 電商環境冷鏈物流路徑優化研究[J]. 特區經濟， 2018（11）： 103-105.

[5] 王勇. 遺傳算法在物流配送線路選擇方面研究[J]. 物流科技， 2018（4）.

[6] 李陽， 李文芳， 馬驪， 等. 混合退火算法求解旅行商問題[J]. 計算機應用， 2014，34（S1）： 110-113.

[7] Valenzuela C L， Jones A J. Evolutionary Divide and Conquer（I）： A Novel Genetic Approach to the TSP[M]. MIT Press， 1993.

【通聯編輯：張薇】