有理有據(jù) 規(guī)范書寫 分分必爭

陳新合

圓是初中幾何中一個簡單而完美的圖形，擁有諸多特性，它既是一個中心對稱圖形，又是一個軸對稱圖形，有無數(shù)條對稱軸。這些特性使得圓與平行線、三角形、四邊形和平面直角坐標系等圖形組合形成綜合性問題。下面通過兩道例題來示范如何規(guī)范解決這類問題，希望對同學們有所幫助。

例1 如圖1，△ABC內接于⊙O，∠B=60°，CD是⊙O的直徑，點P是CD延長線上一點，且AP=AC。（1）求證：PA是⊙O的切線；（2）若PD=5，求⊙O的直徑。

圖1

【思路分析】（1）連接OA，根據(jù)圓周角定理求出∠AOC，由OA=OC得出∠ACO=∠OAC=30°，再由 AP=AC 得出∠P=30°，繼而由∠OAP=∠AOC-∠P=90°，可證得OA⊥PA。

（2）利用含30°角的直角三角形的性質求出OP=2OA，可得出PD=OD=OA，由PD=5可求出⊙O的直徑。

【規(guī)范解答】證明：（1）如圖2，連接OA。

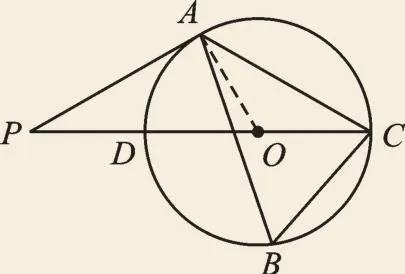
圖2

∵∠B=60°，

∴∠AOC=2∠B=120°，（得1分）

又∵OA=OC，

∴∠OAC=∠OCA=30°，（得1分）

又∵AP=AC，

∴∠P=∠ACP=30°，

∴∠OAP=∠AOC-∠P=90°，

∴OA⊥PA，（得1分）

∵OA是⊙O的半徑，

∴PA是⊙O的切線。（得1分）

解：（2）在Rt△OAP中，

∵∠P=30°，

∴PO=2OA=OD+PD，（得1分）

又∵OA=OD，

∴PD=OA，（得1分）

∵PD=5，

∴2OA=2PD=25，（得1分）

∴⊙O的直徑為2 5。（得1分）

【踩點提示】本題考查了等腰三角形的性質、圓周角定理、切線的判定及含30°角直角三角形的性質。在解題時，我們要明確證明切線的兩種方法：知半徑，證垂直；知垂直，證半徑。本題已知點A在圓上，連接OA得出半徑，選用“知半徑，證垂直”方法來證明。在書寫解題過程時，我們要注意：①在得出∠OAP=90°時，不能直接得出PA是⊙O的切線，必須要寫出OA⊥PA，這一步非常重要，不能省略；②（2）中，所有的解題都是在Rt△OAP中進行的，所以我們在書寫時應明確點出來，使得過程規(guī)范清晰，有利于自己檢查和老師批閱。

例2 如圖3，AB是⊙O的直徑，AC為弦，∠BAC的平分線交⊙O于點D，過點D的切線交AC的延長線于點E。求證：（1）DE⊥AE；（2）AE+CE=AB。

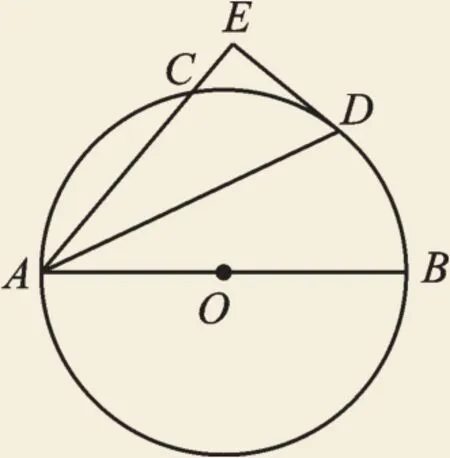
圖3

【思路分析】（1）連接OD，先根據(jù)等腰三角形的性質和角平分線的性質得出∠CAD=∠ODA，從而證得AE∥OD，可知∠E+∠ODE=180°，再由圓的切線性質證得OD⊥DE，可知∠ODE=90°，從而得出∠E=90°，DE⊥AE得證。

（2）根據(jù)角平分線與垂直的組合，容易想到過點D作DM⊥AB，交AB于點M，得到關于角平分線性質的基本圖形，得出DE=DM，再證明△DAE≌△DAM，由全等三角形的性質可得出AE=AM。根據(jù)弦、弧、角之間的關系︵，可︵想到連接CD、DB，由∠CAD=∠OAD可得出C，從而證出CD=BD，結合DE=DM，可證Rt△DCE≌Rt△DBM，根據(jù)全等三角形的性質可得CE=BM，結合AB=AM+BM，即可證得AE+CE=AB。【規(guī)范解答】證明：如圖4。

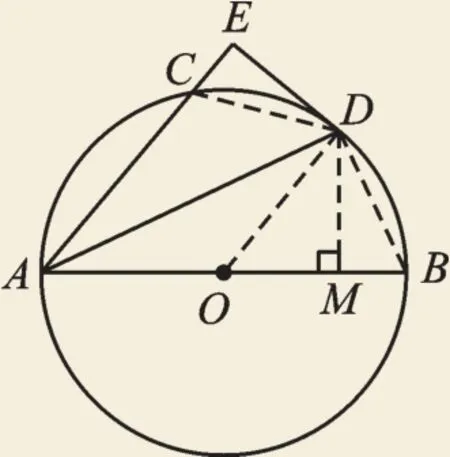
圖4

（1）連接OD，

∵OA=OD，∴∠ODA=∠OAD

∵AD平分∠BAC，∴∠CAD=∠OAD。

∴∠CAD=∠ODA。

1.3.1 套管堵塞。套管堵塞相對常見，由于部分治療肺結核藥物需要輸注濃度較高，而輸液后未能對導管進行徹底清洗，且患者年齡較大，自身合并有一些基礎性疾病，導致患者的血管破壞嚴重，影響液體通暢程度。因此，在治療過程中，輸注部分高濃度、大分子的藥物時要減緩輸液速度，并進行足夠的稀釋，輸注完成之后立即對導管進行清洗，并選擇合適的封管液正確封管，必要時可采取脈沖式封管，最大程度減少導管堵塞情況發(fā)生；如導管已經(jīng)出現(xiàn)堵塞，必須進行回抽，禁止使用注射器進行推注，避免凝固的血栓進入血管引發(fā)不良反應。

∴AE∥OD。（得1分）

∴∠E+∠ODE=180°。

∵DE是⊙O的切線，

∴OD⊥DE。

∴∠ODE=90°。（得1分）

∴∠E=90°。

∴DE⊥AE。（得1分）

（2）過點D作DM⊥AB，交AB于點M，連接CD、DB。

∵AD平分∠BAC，

∴DE=DM，∠AED=∠AMD=90°。

在Rt△DAE和Rt△DAM中，

∴△DAE≌△DAM（HL）。（得1分）∴AE=AM。

∴CD=BD。（得1分）

在Rt△DEC和Rt△DMB中，

∴Rt△DEC≌Rt△DMB（HL）。

∴CE=BM。（得1分）

∴AE+CE=AM+BM。

即AE+CE=AB。（得1分）

【踩點提示】解題時要抓住常見圖形的組合：由等腰三角形與角平分線可得平行線；由垂直與角平分線組合可得角平分線性質定理；見切點，連半徑，得垂直；由圓中弦、弧、角之間的關系，利用等量代換的方法處理線段的和、差問題。在書寫過程時，我們要做到有理有據(jù)，嚴格按照定理要求書寫，不要跳步和省略步驟，比如：例2中由切線的性質可以得到OD⊥DE，不能因為后面需要∠ODE=90°，而跳過OD⊥DE，直接得出∠ODE=90°。證明三角形全等時需要使用大括號，按順序寫出條件，并在后面注明三角形全等的判定方法，這樣使得證明過程條理清晰、簡潔美觀。