基于改進的加權中值濾波與K-means聚類的織物缺陷檢測

張緩緩， 馬金秀， 景軍鋒， 李鵬飛

(西安工程大學 電子信息學院， 陜西 西安 710048)

作為衣著、裝飾、醫用、產業用、航天軍工用品的原料，織物是生活與工業生產中不可或缺的材料，在織物生產中，由于紗線瑕疵、機械故障、人工操作失誤以及生產環境干擾等因素，不可避免地會產生織物缺陷。缺陷的存在對紡織終端產品的質量及價格有著決定性影響，如果缺陷產品應用于航空、軍工及醫用中，將造成不可估量和無法挽回的損失，因此，織物缺陷檢測尤為重要。然而由于各類織物紋理結構復雜，噪聲和細微缺陷之間相似性高，極大增加了缺陷檢測的難度。目前絕大部分的紡織企業依賴人工視覺檢測織物缺陷，傳統的人工檢測易受個人視力、疲勞狀況、情緒、光照等主客觀因素的影響，往往無法確保檢測的精度及準確率，尤其對于紋理復雜、圖案花型多變、顏色差異較小的缺陷，人眼幾乎不能識別，遠遠不能滿足工業生產應用的需求。探索一種有效、具有普適性的織物疵點檢測方法，使其能夠快速且準確地識別各種印花織物的疵點，具有重要的學術價值和應用價值。

近年來，針對織物疵點的檢測算法主要包含 4種方法。基于統計的方法主要包括分形維數、互相關、共生矩陣、局部二進制模式：Conci等[1]運用分形維數理論檢測織物瑕疵；朱丹丹等[2]采用自相關算法計算各個紋理基元和標準模板的相似度，評估格子織物圖像中有無瑕疵紋理基元；然而該類方法對紋理周期性不強的織物檢測效果差。基于頻譜的方法近年來被廣泛應用于瑕疵檢測，主要包括Gabor濾波器[3-4]、小波變換[5]和傅里葉變換[6]：Kumar等[7]研究了幾種不同的利用Gabor小波特征進行紋理材料表面檢測的方法；Tsai等[8]利用傅里葉模型提取織物瑕疵的傅里葉特征，進而實現疵點分割；該類方法可有效提取瑕疵的特征，但對于方格條紋織物檢測效果不佳，自適應性不強。基于模型的方法有自回歸模型、馬爾科夫隨機場模型等：Hajimowlana等[9]使用一維自回歸模型提取誤差區域生成疵點形狀；李敏等[10]應用改進的高斯混合模型，通過分塊建模思想有效識別出彩色紋理織物表面疵點；可以看出，基于模型的方法適合織物紋理之間的分類，雖然可識別紋理結構相對簡單、顏色單一的織物瑕疵，但在瑕疵識別研究中相對于統計法和頻譜法應用較少，另外該類方法的算法復雜度高，檢測時間較長。基于學習的方法常見的有應用卷積神經網絡、自編碼網絡[11]：Yapi等[12]提出了一種新穎的基于監督學習的方法；Tsang等[13]提出的Elo評級方法，在點形和星形圖案的織物圖像中被證明有很好的效果；Li等[14]基于Fisher準則將含有疵點和不含疵點的織物圖像進行分類，表明該方法在復雜的提花經編織物上有更好的結果；基于學習的方法需要觀測者對大量圖像進行標記質量分數來訓練模型參數，而主觀標記質量分數存在不精確、費時耗力等缺陷。

綜合以上分析可知，現有檢測方法很難有效描述復雜多樣的織物紋理，且具有很高的運算復雜度，自適應性不強，致使檢測效果不明顯。針對織物組織紋理結構復雜、花型繁多、材質多樣的特點，如何有效檢測出疵點仍然是研究的熱點。本文提出改進的加權中值濾波與K-means聚類相結合的方法，以提高算法對不同織物紋理的適應性，在抑制背景紋理的同時通過聯合直方圖以及中位跟蹤平衡算法顯著提高濾波速度；利用K-means聚類標記出疵點與非疵點區域，以檢測方格、點形、星形、平紋、斜紋等各種紋理織物的疵點。

1 織物疵點檢測方法

本文織物疵點檢測流程圖如圖1所示。首先采用快速加權中值濾波對圖像進行平滑處理，改善織物紋理和噪聲對疵點檢測的影響，并提高圖像預處理速度；其次，利用K-means均值聚類算法對平滑之后的圖像進行聚類，將圖像標記為疵點區域和非疵點區域，進而實現瑕疵的檢測。

1.1 加權中值濾波

織物紋理是織造過程中緯線與經線有規律的交織形成的周期結構，具有隨意多樣的特點，這給織物疵點的檢測帶來很大的困難。加權中值濾波處理織物疵點圖像可更好地保留疵點特征信息。

加權中值濾波器可看作是一個運算符，是用本地窗口中相鄰像素的加權中值替換當前像素。形式上，在處理圖像I中的像素p時，僅考慮以p為中心，半徑為r的局部窗口R(p)內的像素，與傳統未加權中值濾波器不同，對于每個像素q∈R(p)，加權中值濾波基于對應特征圖f中像素p和q的親和度將其與權重Wpq相關聯，如式(1)所示。

Wpq=g(f(p),f(q))

(1)

式中：f(p)和f(q)為f中像素p和q處的特征；g為相鄰像素之間的典型影響函數，可以是高斯 exp{-‖f(p)-f(q)‖} 或其他形式。

將I(q)表示為圖像I中的像素q和n=(2r+1)2處的值作為R(p)中的像素數，將R(p)中的所有像素的值和權重表示為(I(q),Wpq)。按升序的規則對值進行排序，像素p的加權中值運算符返回一個新的像素p*，I(p)由I(p*)代替。這個過程得到的p*如式(2)所示。

(2)

式中，k為像素數。該定義對于p*之前的所有像素，意味著相應權重的總和應該是所有權重相加的一半，f映射通過式(2)確定權重。

1.2 改進的加權中值濾波

加權中值濾波處理紋理織物疵點圖像時不能解決重復進行訪問排序的問題，比較耗時，在疵點檢測實時性要求較高的情況下難以應用，因此，采用以下方法改進加權中值濾波[15]，減少背景紋理信息對檢測的影響，同時提高檢測速度以滿足工業生產的需求。

1.2.1 聯合直方圖

將聯合直方圖與滑動窗口策略相結合，以實現預處理速度的提升。聯合直方圖是一種常規但非常有效的二維直方圖結構，用于存儲像素數，如圖2所示。在2-D聯合直方圖H中，將像素q放入第f行和第i列的直方圖中，整個聯合直方圖構造如式(3)所示。

我父親1918年初生人，屬馬。要是活著今年整一百歲了。我奶奶家當年是做生意的，經濟上挺富裕。1916年她16歲那年，在讀私塾的時候認識了我爺爺。當時我爺爺家境并不好，只因為他叔叔是教書先生，他才能跟著讀私塾。那個年代婚姻都是家長做主，可我奶奶有大小姐脾氣，再加上民國了讀書了，思想相對開放了，非要嫁我爺爺不可。一來二去，家里看實在攔不住了，只能勉強同意。轉年，我爺爺家下了聘禮，我奶奶下嫁了我爺爺。

H(i,f)=#{q∈R(p)I(q)=Ii,f(q)=ff}

(3)

式中：運算符#為計算元素的數量，該計數方案即使在窗口移動時也能實現權重的快速計算。對于屬于窗口中(i,f)的任何像素，考慮濾波器中心p，其權重可立即計算為g(ff,f(p))，通過遍歷聯合直方圖，可獲得像素權重值為i的所有像素的總權重，如式(4)所示。

(4)

式中，Nf為不同特征的總數。

圖2 聯合直方圖圖解Fig.2 Joint-histogram illustration

算法以掃描線順序處理輸入圖像，每個位置執行2個步驟。步驟1為中值查找：首先遍歷聯合直方圖，根據式(2)計算權重,將他們相加得到第1遍的總權重wt；然后進行第2遍遍歷，計算總權重wt的一半的加權值，并輸出相應的像素值。步驟2為移位和更新：如果不是此圖像的結尾，將濾波窗口移動到下一個位置。計數離開窗口的每個像素相應減少的單元格，每移出1個像素就增加1個來更新聯合直方圖。

算法加快了中值濾波效率，但由于步驟1需要遍歷直方圖，占用更多的時間。為進一步改善，采用中位跟蹤平衡算法，使步驟1能夠加速到300～2 000 倍。

1.2.2 中位跟蹤平衡算法

根據定義，在累積權重達到總權重一半的位置處得到加權中位數，在當前濾波器中認為在該位置找到加權中值并作為切點c，如圖3所示。其中左邊的權重總和等于右邊權重的總和，wl和wr之間的差異接近于零，有助于通過求解找到加權中位數。

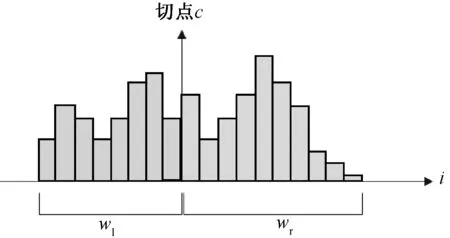
圖3 切點與平衡點的分布Fig.3 Illustration of balance and cut point

使用平衡算法，可直接獲得窗口的平衡點b，如式(5)所示。

(5)

式中，B(f)測量c兩側特征ff的像素數是否平衡。通過計算像素數差異的輕量級平衡度量，可判斷是否找到加權中位數，以此代替累積權重算法。

1.3 K-means聚類

預處理削弱了織物紋理背景的影響，疵點得以突顯，同時分析織物本身的特性可知，織物疵點圖像可看作是疵點和織物紋理二類簇的疊加。根據該特點，采用K-means算法對預處理后的圖像實現織物疵點的分割，如圖4所示。

圖4 K-means算法對織物疵點進行分割Fig.4 Segment of fabric defect by K-means. (a)Texture part; (b)Defect part; (c)Fabric defect image

設xi為簇Ci中的數據對象，ci為簇Ci的中心點(均值)，通常所用的目標函數如式(6)所示。

(6)

式中，Je為輸入數據對象與其所在簇的中心點的平方誤差總和。

K-means算法過程如下：1) 隨機選擇k個對象作為初始聚類中心；2) 計算每個樣本點到各個聚類中心的歐式距離，以距離為依據將各個樣本點分配到與其最近的類中；3) 重新計算每個類別所有樣本點的均值，更新聚類中心；4) 重復過程(2)、(3)，直到目標函數收斂為止。

利用K-means聚類算法的特性，對織物圖像的像素灰度值進行聚類計算，判斷織物圖像的像素值屬于疵點類別還是非疵點類別，實現缺陷的分割。

2 結果與討論

為驗證所提出的紋理織物疵點檢測算法的可行性，采用香港理工大學自動化實驗室[16]的3類圖案織物(方格織物、點形織物、星形織物)樣本及德國TILDA織物紋理數據庫其他類型的織物疵點樣本進行測試。

在中值濾波階段，影響檢測結果的2個參數為：改進的快速加權中值濾波的r(窗口半徑)和σ(標準偏差的高斯內核值)。以方格織物為例，分析各參數對織物圖像檢測結果的影響，如圖5所示。可知：窗口半徑r越小，織物背景紋理對檢測結果的干擾較大；而r過大又會造成檢測結果失真，故選取r=13.0。圖6示出不同σ值對應疵點檢測結果。可知：σ越小，背景紋理越不易被抑制，疵點檢測越困難；σ越大，檢測到的疵點面積有所變化，部分背景被當作疵點區域檢測出來，導致疵點區域過于完整與連續，故選取σ=135.0。針對不同紋理類型的織物，其參數選擇不同。參數范圍如表1所示。

圖5 不同窗口半徑r對應的檢測結果Fig.5 Detection results of different r. (a)Grid beheaded; (b) r=10.0; (c) r=13.0; (d) r=15.0

圖6 不同σ值對應的檢測結果Fig.6 Detection results of different σ. (a) Box-patterned oil; (b) σ=100.0; (c) σ=135.0; (d) σ=500.0

表1 改進的快速加權中值濾波的參數設置Tab.1 Parameters setting for modified faster weighted median filter

圖7 本文方法對部分方格點形及星形織物樣本檢測結果Fig.7 Some results of square, dot, star fabric defect detection by method of this paper. (a) Fabric original image; (b) Result by using improved weighted median filtering; (c) Detection result

實驗過程中選擇多種紋理的多種疵點進行檢測，其部分檢測結果如圖7、8所示。同時，將本文方法與文獻[3]所述的Gabor濾波法、文獻[17]所述的Frangi濾波器和模糊C均值結合的方法進行比較，結果如圖9所示。由圖9(b)可知，Gabor濾波法不能完全地去除紋理對檢測結果的影響，噪聲干擾比較大；由圖9(c)可以看到，疵點區域膨脹或者部分疵點區域丟失，對疵點的細節信息檢測不準確，所以Frangi濾波器和模糊C均值結合的方法不能很好地看到效果。綜上，本文提出的改進的快速加權中值濾波不僅可很好避免背景紋理的干擾，突出疵點信息，而且使用 K-means 聚類后能更清晰地突出疵點，可視化較好，準確率高(見圖9(d))。

為驗證算法的分割精度，利用準確度(ACC)、真陽性率(TPR)、假陽性率(FPR) 3個參數進行量化對比，如式(7)～(9)所示。

(7)

(8)

(9)

式中：TP為真正例；FN為假反例；FP為假正例；TN為真反例。

算法對每種類型紋理織物采取120張圖片進行測試，求取檢測結果平均值。表2示出不同類型的紋理織物的疵點檢測所用的平均時間，檢測結果準確率對比如表3所示。

表2 使用不同方法檢測所用平均時間Tab.2 Comparison of average time by three different methods s

由表2和表3可以看出，本文提出的方法檢測準確度可高達到97%，整體可靠度水平較高。從算法的執行速度來看,本文所提出的方法在檢測各類紋理織物時，與文獻[3]、[17]方法相比，檢測時間明顯縮短。

表3 使用不同方法的準確率對比Tab.3 Comparison of accuracy by three different methods

3 結 論

為減少織物紋理信息對疵點檢測的影響，對中值濾波進行改進，將聯合直方圖與滑動窗口策略相結合，實現預處理速度的提升；利用K-means聚類算法將織物的疵點和非疵點進行分類檢測，避免復雜的確定分割閾值環節，直接完成疵點檢測，進一步提升了檢測效率；本文提出的方法可對方格、點形、星形、平紋、斜紋等紋理織物的疵點進行檢測。實驗結果表明提出的方法效果較好，具有較高的可靠性。