臥式容器中液體體積的計算
丁 浩,劉 輝,劉勇營,陳先進
(浙江化工院科技有限公司,浙江 紹興 312369)
臥式容器由于安裝和使用方便等諸多因素,被廣泛應用于化工、石油、冶金等行業中。在生產和貯運過程中,經常需要根據液位來計算出容器中的液體體積,以方便計量和操作。臥式圓筒容器內液體體積的計算是與其封頭形式有關系的,因封頭形式不同計算公式有所不同,封頭形式主要有平封頭、橢圓封頭蝶形封頭、球形封頭等幾種類型,但應用最廣泛的主要為橢圓型封頭臥式容器。本文以數學分析的方法詳細推導出橢圓型封頭臥式容器內液體體積的計算公式,以便準確地計算出容器的介質質量。
1 橢圓型封頭臥式容器液體體積計算
橢圓型封頭臥式容器[1]由直筒和橢圓型封頭兩部分組成,如圖1所示。
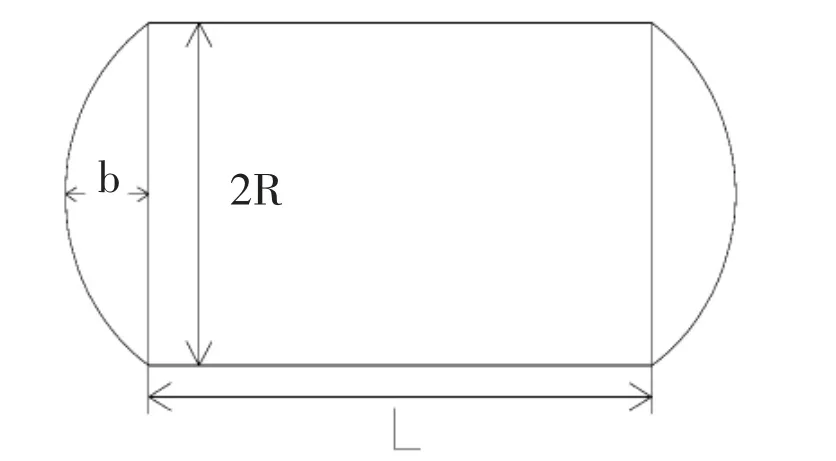
圖1 臥式容器結構示意圖
圖1 中臥式容器直筒部分的長度為L,半徑為R,橢圓型封頭曲面高度為b。
整個容器內物料的體積為直筒部分物料體積和兩個橢圓型封頭物料體積之和,即,式中V為臥式容器總體積,V1為直筒部分體積,V2為單個橢圓型封頭體積。
1.1 直筒部分液體體積
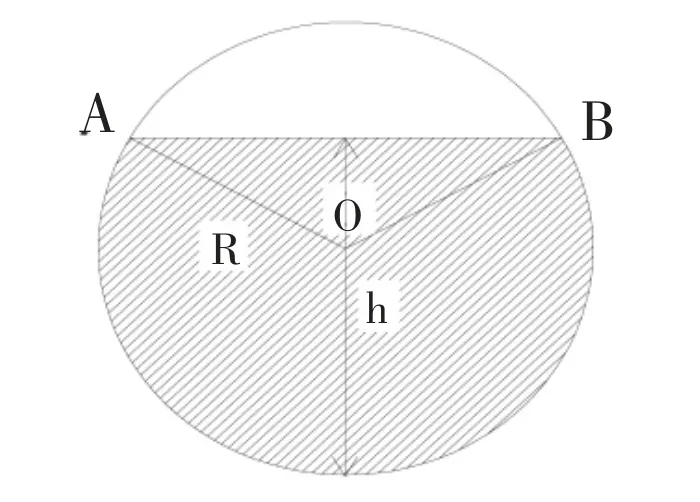
直筒內裝有高度為h的液體體積等于液體淹沒直筒橫截面的弓形面積乘以直筒部分長度。直筒部分橫截面結構(h<R)如圖2所示。
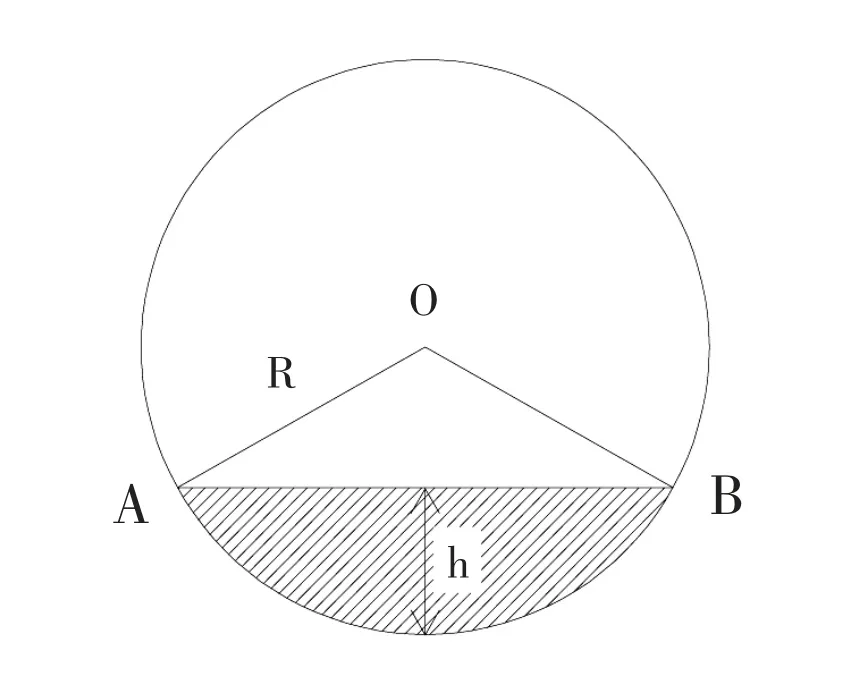
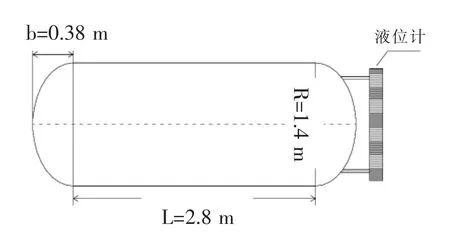
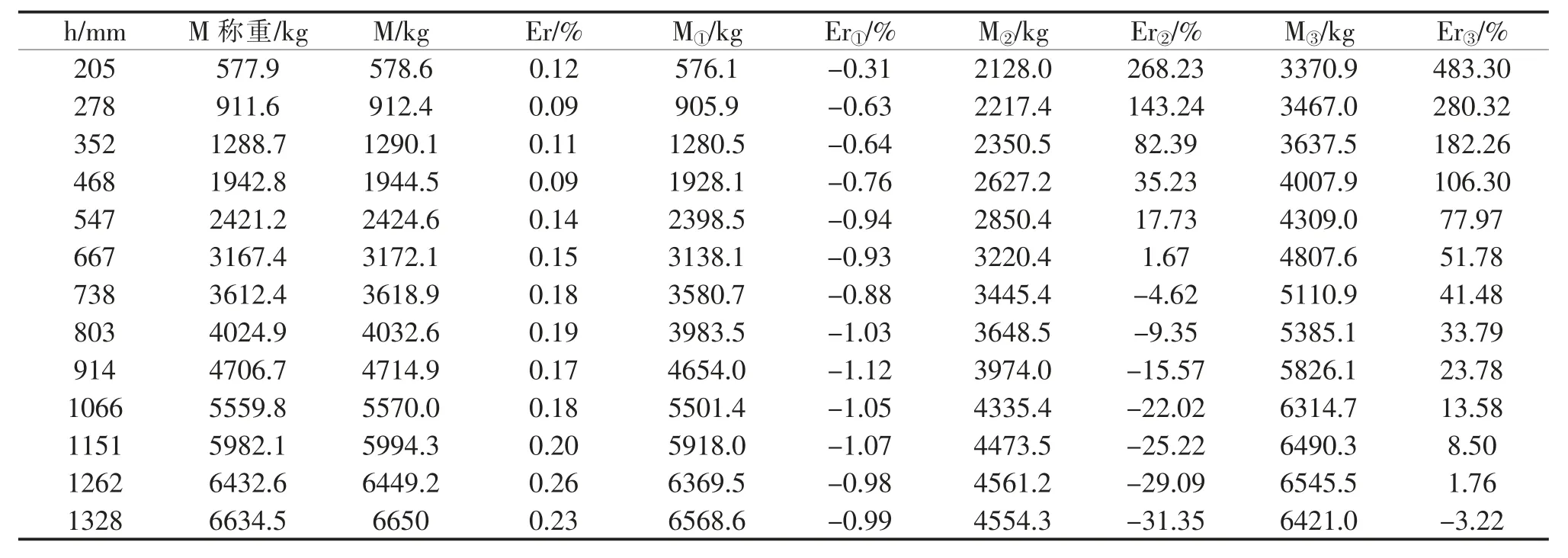
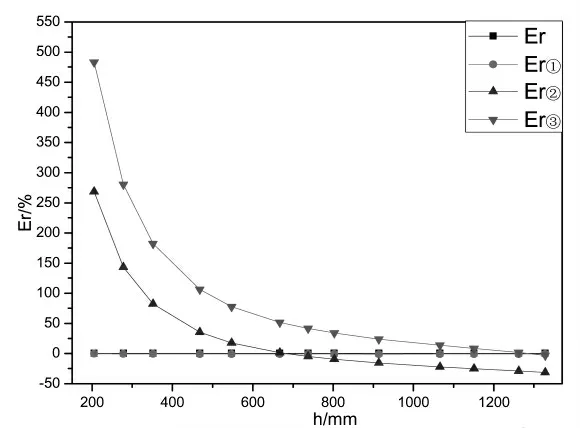
圖2 直筒橫截面結構示意圖(h 橫截面中弓形面積為: 則直筒部分液體體積 當液位高度h>R時,橫截面結構如圖3所示。 圖3 直筒橫截面結構示意圖(h>R) 對橢圓型封頭[2-3]建立如圖4所示的空間直角坐標系。其中封頭部分的長軸半徑為R,短軸半徑為b。 圖4 直筒橫截面結構示意圖(h>R) 在XOY面上的投影方程為x2+y2=R2,封頭方程為 1.3.1 液位高度h<R時 1.3.2 液位高度h>R時 對于橢圓型封頭臥式容器內液體體積[4-5]的計算,還可通過先計算K=h/D值,然后查表得出容積系數,用筒體及封頭部分的總容積乘以容積系數得出,其中D=2R。下面介紹幾個常用的快速計算公式。 (其中V為儲槽總容積,單位m3) 現結合中試試驗裝置平臺,通過向橢圓型封頭臥式液堿儲槽中補加液堿(30%氫氧化鈉溶液,密度為1330 kg/m3)的方式對本文推導出的液體體積計算公式及常見的計算公式進行驗證,并進行誤差對比分析。液堿儲槽結構示意圖如圖5所示。 由于液位計下端口至儲槽底部有100 mm的液位顯示盲區,故實驗中液堿液位始終高于100 mm。液堿儲槽配備稱重遠傳及液位遠傳模塊,實驗開展前已完成校正和調試工作。 圖5 液堿儲槽結構示意圖 打開液堿儲槽進料閥門,并保持閥門開度不變,向儲槽中勻速進料。當儲槽內液位高度達到1.35 m時,立即關閉進料閥門,停止補加。為減少實驗誤差,進行多次實驗并取平均值。液位及重量數據在每次實驗結束后,從DCS后臺系統中調取實驗數據。實驗數據及誤差分析對比情況詳見表6。 表6 實驗數據及誤差分析對比 圖7 誤差對比圖 從圖7中可以明顯看出相對誤差Er②和Er③數值均隨著液位高度h的增大而逐漸減小,說明在低液位時,兩個經驗公式V①和V②的計算結果相對誤差較大,與實際工況偏離嚴重。但是隨著液位高度的逐漸增大,其相對誤差逐漸減小。當液位高度達到80%后,Er②和Er③平均值分別為28.56%和4.57%。 圖7中相對誤差Er和Er①較小且數值隨著液位高度h的逐漸增大而保持平穩,說明本文中推導出的體積計算公式V和經驗公式V①在全液位高度范圍內與實際工況更加吻合。但從表6中可以計算出,Er的平均值為0.16%,Er①的平均值為-0.87%,所以本文中推導出的體積計算公式V在實際工況下計算相對誤差更小。 本文以數學分析的方法推導出臥式容器內不同液位高度下對應的液體體積計算公式,并通過實驗對其進行驗證和誤差分析,實驗結果表明在全液位量程范圍內相對誤差僅為0.16%,與實際工況更為接近,同時可根據比重確定容器內的工況質量。此次公式推導為中試試驗及生產裝置提供了更加準確的計算方式,具有良好的實踐意義。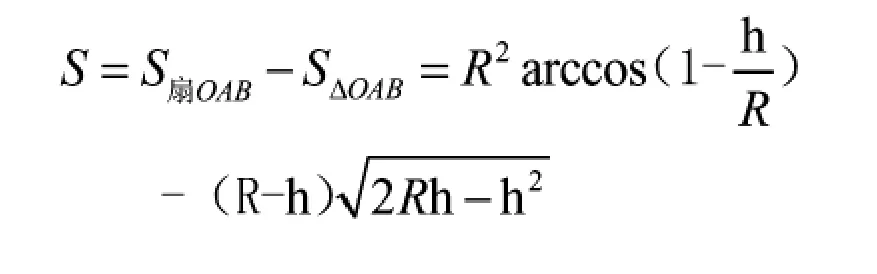
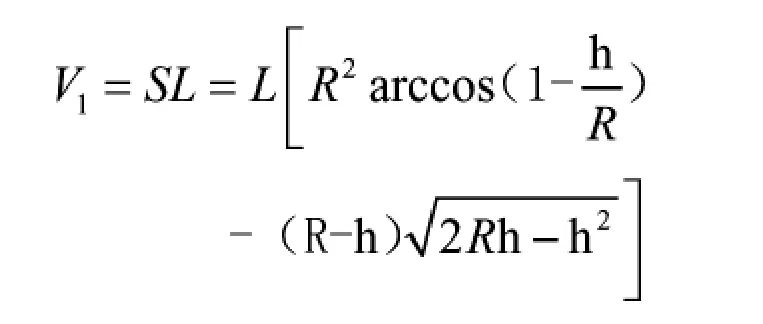
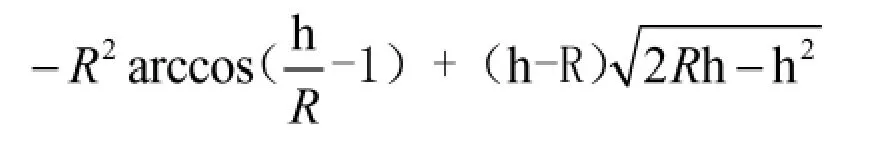
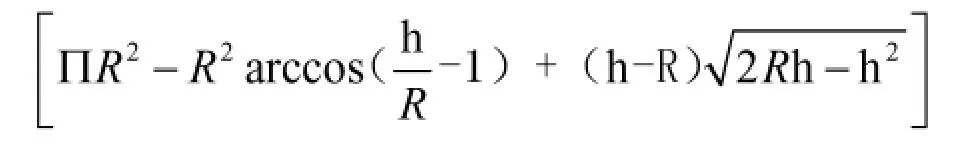
1.2 橢圓型封頭部分液體體積
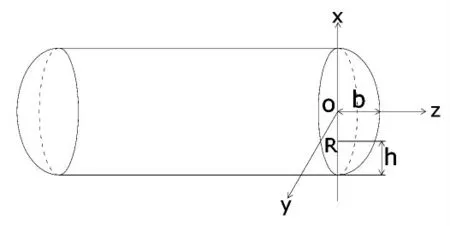
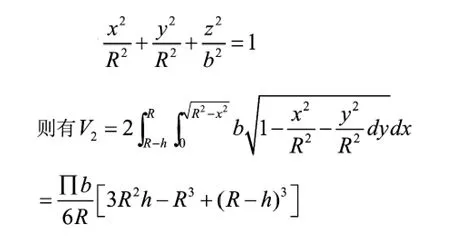
1.3 橢圓型封頭臥式容器液體體積
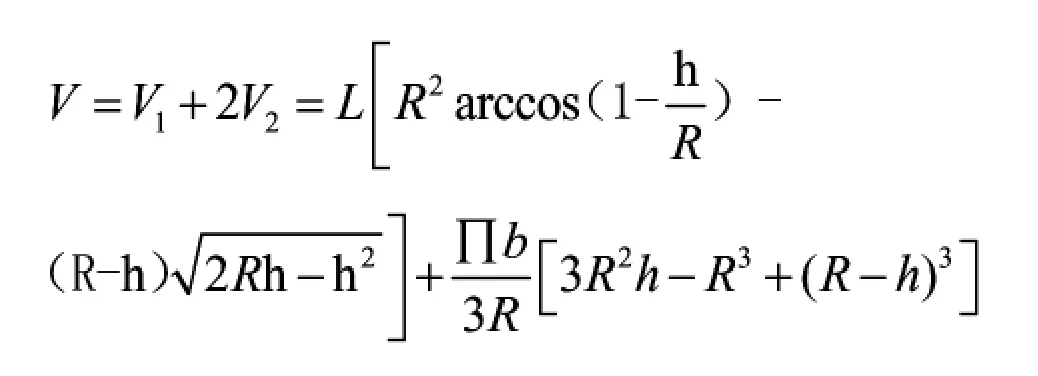
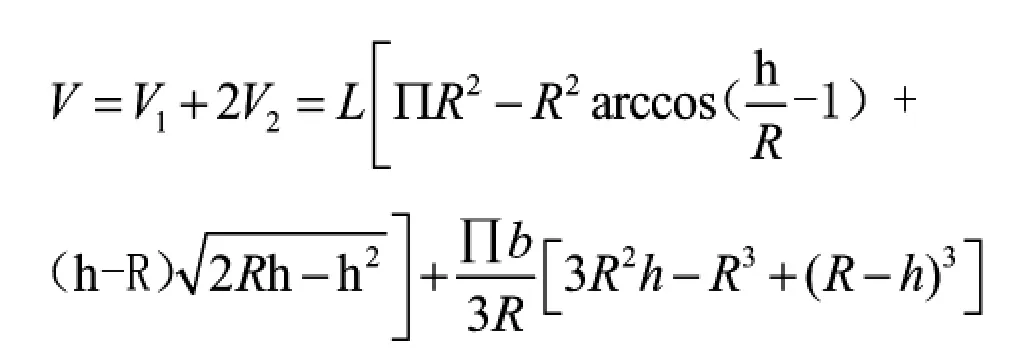
2 常見幾種液位體積計算公式
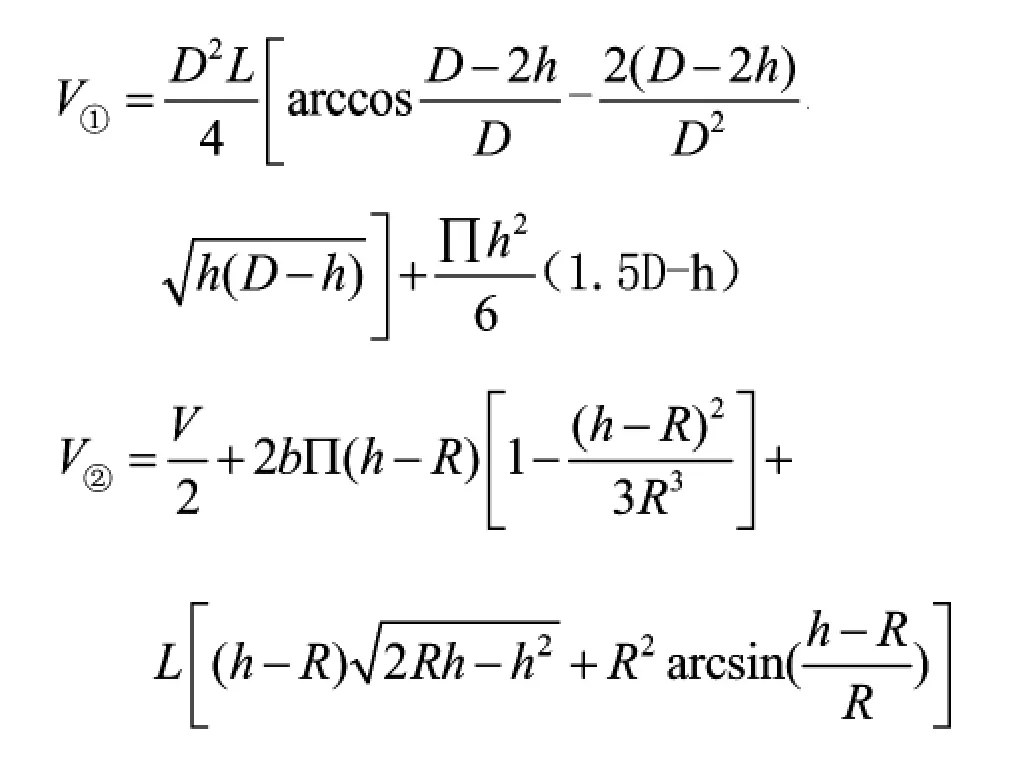
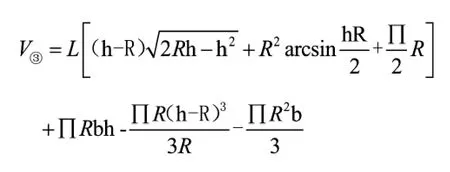
3 實驗驗證及誤差分析
4 結語

