單參多極值點復解析多項式映射迭代函數系

陳 寧,關博文,海智剛

(沈陽建筑大學 信息與控制工程學院,沈陽 110168)

1 引 言

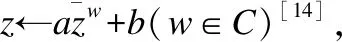
2 IFS定義與f(z)=zn+cz的數學特性

2.1 線性IFS的定義

平面上生成分形的迭代函數系(IFS),通常由兩個或兩個以上的線性仿射壓縮變換組成.文獻[4]給出了平面上IFS的定義:在歐氏空間(R2,ρE)上的一組線性壓縮映射ωn:R2→R2,n=1,2,…,N,構成了一個IFS,其中:

ωn(x,y)=(anx+bny+en,cnx+dny+fn),n=1,2,…,N

(1)

式(1)中的(x,y)為平面上的點的橫向和縱向坐標;an,bn,cn,dn,en,fn∈R1為實數.

文獻[4]指出式(1)必須滿足3個壓縮條件:an2+cn2< 1,bn2+dn2< 1和an2+bn2+cn2+dn2<(andn-cnbn)2,才是一個可以生成分形的有效IFS.

在研究中筆者注意到:由于上述IFS中每個變換都是平面上的壓縮變換,且每個壓縮變換的吸引域都是除無窮遠點外的整張平面,這些變換在動力平面上的公共吸引域與IFS中單個變換的吸引域相同.因此,IFS的分形或其近似分形可以通過選取平面上的任意有界閉集作為初始迭代集,也可以從平面上的任意有界點作為初始迭代點,通過隨機迭代得到分形或其近似值.

2.2 復映射f(z)=zn+cz的數學特性

動力平面上的原點(0,0)是復映射族f(z)=zn+cz的不動點.由于復映射的1階導數為f′(z)=nzn-1+c,所以,當|c|<1時,點(0,0)是復映射的吸引不動點;當|c|>1時,點(0,0)是復映射的排斥不動點.如果該映射當|c|>1時有非零不動點f(pj)=pj,則取:

(2)

使:

即復映射f(z)=zn+cz有n-1個旋轉對稱不動點.由于動力平面上的復映射f(z)=zn+cz的極值點zc為其1階導數為0的點,使f′(zc)=0,有:

(3)

式(3)表明,與復映射f(z)=zn+c只有1個極值點不同,復映射f(z)=zn+cz在動力平面上有n-1個旋轉對稱的極值點.

3 復映射f(z)=zn+cz的M集與充滿Julia集

圖1 復映射族f(z)=zn+cz的M集Fig.1 M sets of the complex mapping family of f(z)=zn+cz

易于證明復映射族f(z)=zn+cz在動力平面上是n-1旋轉對稱的,因此,相應的充滿Julia集在動力平面上也是n-1旋轉對稱的.圖2說明在圖1的M集各圖中取參數構造出的充滿Julia集圖形是在原點處分叉的.復映射族f(z)=zn+cz的充滿Julia集圖形結構與參數在M集上的幾何對稱位置有關.雖然對稱位置上參數的迭代映射的吸引周期軌道條數不同,但吸引周期點的“總和”p相同,所以,這些參數下的充滿Julia集除了相差旋轉角度以外,他們的充滿Julia集的圖形結構是完全相同的,如圖2(a)與圖2(b)、圖2(d)與圖2(e)以及圖2(h)與圖2(i)所示.在復映射族f(z)=zn+czM集的芽苞上的芽苞區域選取參數c,相應的充滿Julia集有多級分叉結構,如圖2(c)與圖2(f)所示.圖2(g)是M集上A序列周期芽苞參數的充滿Julia集.

在圖1所表示的復映射族f(z)=zn+cz的每一個M集中,均有2個1周期參數區域:1個是以原點為中心的“1_1”參數區域,另一個是中心在正實軸上的“(n-1)_1”參數區域.由構造M集時參數區域的標記方法可知,采用1_1區域中參數c構造的迭代映射,在動力平面上只有1個吸引周期不動點,通過式(3)計算的(n-1)個極值點的軌道都到達原點(0,0).由前面討論得到1_1區域中的參數|c|<1,且充滿Julia集的幾何特點是包含原點在內的并以原點為中心的(n-1)旋轉對稱實心區域.圖3(a)表示了n=4時,在圖1bM集的1_1區域取參數c3時,動力平面上的充滿Julia集,以及根據式(3)計算出的3個極值點迭代到吸引不動點(0,0)的軌道,充滿Julia集的幾何特點是以原點為中心的3旋轉對稱實心結構.

如果在正實軸上的“(n-1)_1”芽苞區域選取參數c構造迭代映射f(z)=zn+cz,這個區域中參數下的映射在動力平面上有(n-1)個旋轉對稱分布的1周期吸引不動點(pj,j=0,1,2,…,n-2),可以通過式(2)直接計算得到,也可以通過式(3)的(n-1)個旋轉對稱分布的極值點(zcj,j=0,1,…,n-2)的迭代得到(如圖3(b)和圖3(c)所示).(n-1)個吸引不動點在動力平面上有(n-1)個旋轉對稱分布的吸引域,形成在原點處有(n-1)個旋轉對稱分叉的充滿 Julia集圖形結構.由于這個參數區域的參數模值大于1,所以原點是這個迭代映射的斥性不動點,是充滿Julia集的邊界上的(n-1)個旋轉對稱分布吸引域的邊界的交點.圖3(b)和圖3(c)分別為取自圖1(b)中的n=4 M集的3_1周期芽苞上的參數c4和c5的迭代映射在動力平面上的充滿Julia集圖形,3種顏色分別代表迭代映射的3個吸引不動點的吸引域,每個吸引域上給出了極值點zcj、吸引不動點pj以及從zcj到pj的迭代軌道.

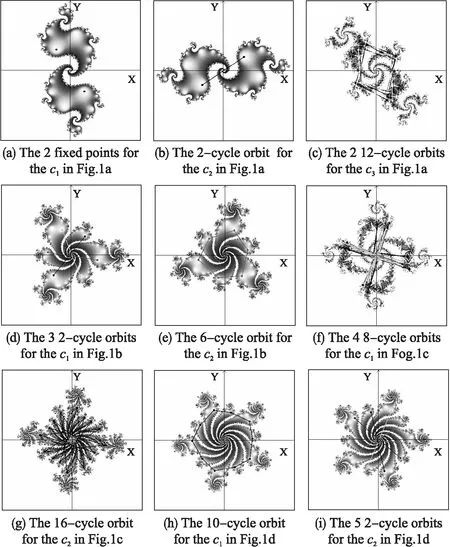
圖2 復映射f(z)=zn+cz的充滿Julia集及其軌道Fig.2 Filled-in Julia sets and the orbits of f(z)=zn+cz

圖3 在復映射f(z)=z4+cz M集的″1_1″與″3_1″周期芽苞區域中選取參數生成的充滿Julia集及3個極值點的迭代軌道、吸引不動點Fig.3 Filled-in Julia set, 3 iterating orbits and 3 attracting fixed points respectively from the 3 parameters chosen from the ″1_1″and″3_1″cycle bud regions of the M set of f(z)=z4+cz

4 構造復映射族 f(z)=zn+cz IFS及分形

如前所述,復映射族f(z)=zn+cz的M集上有2個可以構造具有吸引不動點迭代映射的參數區域“1_1”和“(n-1)_1”,但是可以構造分形的有效IFS的參數區域是“(n-1)_1”.雖然在“1_1”參數區域選取參數可以在動力平面上構造出具有吸引不動點的充滿Julia集,但是如果在“1_1”參數區域選取N個參數構造IFS,由于IFS中的所有N個迭代映射的吸引不動點都是原點(0,0),而且原點是復映射族f(z)=zn+cz的零點,所以無論怎樣隨機挑選IFS中的迭代映射去迭代吸引不動點(0,0),迭代軌道永遠停留在原點(0,0)處,即M集的“1_1”參數區域不能用于有效構造IFS.

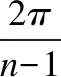
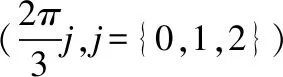
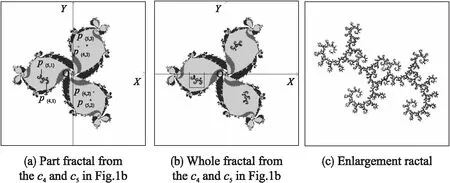
圖4 在復映射f(z)=z4+cz的M集的3_1芽苞區域選參數構造分形Fig.4 Construction of the fractal from f(z)=z4+cz with the parameters chosen on the 3_1 cycle bud region in the M set

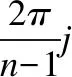
圖5是n=3,4,5,6時,放大圖1中的各“(n_1)_1”芽苞參數區域的M集圖形.圖6是采用上述算法,分別由圖5中各圖的參數且N=2或3或4時,由復映射f(z)=zn+cz構造的非線性IFS的n-1旋轉對稱分形圖的一個旋轉對稱部分的放大分形圖.

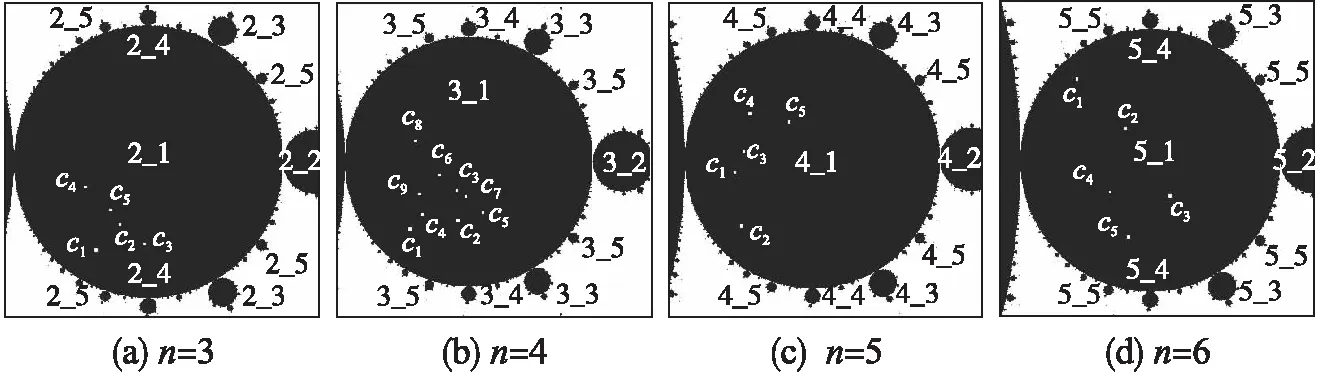
圖5 復映射族f(z)=zn+cz M集的(n-1)_1芽苞區域放大圖Fig.5 Enlargement of the (n-1)_1 cycle bud region of the M sets of f(z)=zn+cz

5 結 語

單參復映射族f(z)=zn+cz具有(n-1)個極值點,在參數平面上的M集由考察參數下相應迭代映射的(n-1)個極值點的迭代軌道有界構造.用符號 “number1_number2”表示M集1個周期芽苞參數區域中的所有參數都可以在動力平面上構造出具有number1條number2吸引周期軌道的迭代映射.

該映射族的M集在對稱位置參數下的迭代映射在動力平面上的動力學特性可以不同,但是這些迭代映射所有吸引周期軌道的吸引周期點的“總和”相同,其充滿Julia集圖形結構相同.

圖6 來自復映射族f(z)=zn+cz的分形Fig.6 Fractals from the f(z)=zn+cz

該映射族在n≥3時的M集中有2個1周期參數區域:包含原點(0,0)的單位圓區域“1_1”和正實軸上的單位圓外的區域“(n_1)_1”.

由于“1_1”區域中的參數|c|<1,相應迭代映射的(n-1)個極值點的迭代軌道都被吸引不動點(0,0)吸引,所以,在這個區域選取N(N≥2)個參數構造不出有效的IFS.

如果在“(n_1)_1”參數區域選取N個參數構造迭代映射,由于|c|>1,原點(0,0)退化成斥性不動點,而(n-1)個極值點的迭代軌道被(n-1)個旋轉對稱分布的吸引不動點吸引,所以,N個迭代映射的充滿Julia集均是以原點(0,0)為交匯點的(n-1)個旋轉對稱分叉圖形.如果N個迭代映射的N(n-1)個吸引不動點在N個充滿Julia集的公共吸引域X內,則N個迭代映射構成了非線性IFS:{X,f(z)=zn+ciz,i=1,2,…,N}.

利用本文提出的雙隨機迭代法可以大量構造來自于復映射族f(z)=zn+cz的具有(n-1)旋轉對稱分形.