基于扇形優化Dijkstra算法的艦船最佳導航路線分析?
田茹會
(陜西能源職業技術學院 咸陽 712000)
1 引言
艦船作為一個危險的工作場所,一旦出現不規范作業或受海上因素的影響便可能造成無法挽回的巨大損失[1~4]。如果現場人員能夠在遇到災害時快速選擇最優路徑導航,則可以顯著提升生還概率[5]。由此可見,采用合適的方法來求解得到最佳路線已經成為一項具有重大現實意義的課題。
采用傳統Dijkstra算法來搜索最佳路徑存在較大的盲目性,王玉琨[6]等利用經過扇形優化的Dijkstra算法來求解路線,使搜索速度獲得顯著提高;同時,楊林[7]在研究煤礦瓦斯事故的應對方案過程中,對導航實施“當量計算”并采用Dijkstra最佳路徑算法求出最佳導航路徑。王磊等采用Dijsktra算法來完成對路徑的導航分析功能,同時粒子群算法來規劃真實路徑的選擇過程,通過為指定節點區域確定較優路徑來實現路徑規劃的目的。薛峰會等研究了對船舶導航路徑計算過程進行優化的方法,以Dijkstra算法優化了航行規劃圖上所有節點之間的航行路徑。本文根據以上研究結果,對導航當量長度以及導航速度進行了深入探討,并通過Dijkstra算法構建得到了選擇艦船最佳導航路線的模型。
對導航當量長度以及導航速度進行了深入探討,給出了扇形優化Dijkstra算法進行分析流程,并進行了應用示例。
2 導航當量長度
選擇Dijkstra算法來求解最佳導航之前,應先把所有導航表示成統一的當量長度。先根據艦船導航中的實際網絡狀態及其影響程度來得到各個導航對應的影響因子。之后,考慮到海上作業環境具有較大的復雜性與特殊性,因此實際導航影響因子會受到多種因素的共同影響,本文將從以下各個角度對導航速度進行分析,包括導航有效寬度、高度、風向、風速及其水流速程度。針對上述各項影響因素,依次采用系數α1、α2、α3、α4、α5進行表示,并得到下述表達式[8]
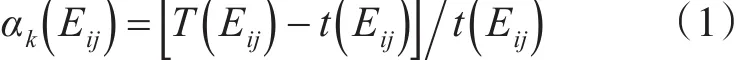
在式(1)中,Eij代表連接節點 i與 j的導航;α(Eij)是導航Eij中包含的影響因子系數;T(Eij)是包含此該影響因子的情況下經過導航Eij所需的時間,單位s;t(Eij)是不包含此影響因子時經過導航Eij所需的時間,單位s。
導航Eij綜合影響程度系數α(Eij)取決于所有因子影響程度系數進行加和所得的結果,表示為如下的形式:
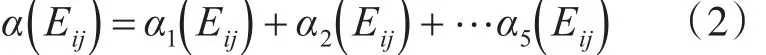
采用統一測試條件完成現場模擬與實測過程,并對T(Eij)與t(Eij)測試結果進行取平均,結合式(1)求解出對導航具有影響的各個因子系數,之后計算得到影響因素的系數之和,再通過式(2)求解得到導航的綜合影響程度系數。
當導航的影響因子被確定之后,則可以根據導航真實長度與總影響程度系數來獲得當量長度,表達式如下:
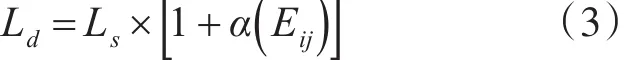
從上式中可以看到,Ls是對導航進行實際測試所得的長度,單位m;Ld代表導航當量長度,單位m;α( )
Eij代表導航總影響程度系數。以同樣的條件進行現場模擬測試與仿真,經多次測試得到的Ls平均值,再通過式(3)計算導航當量長度。計算連接受災地點與避難地點之間的各個可通行導航對應的當量長度,并尋找具有最小當量長度的路徑,再以此路徑作為最佳導航路徑。
3 扇形優化Dijkstra算法
采用傳統Dijkstra算法進行處理時,是先選擇一個中心位置再通過不斷增加節點距離的方式得到最佳路徑的搜索算法,需完成各個標定路線的搜索之后才可以進行統計運算,實際計算量非常大,因此導致搜索速度明顯變慢,同時也使得搜索過程變得更加盲目。為了克服Dijkstra算法的以上缺陷,本文選擇經過扇形優化的Dijkstra算法進行分析,經過優化后的Dijkstra算法所采用的核心處理思想是按照人員定位結果來得到艦船導航的源點,根據設定的導航目標點以直線連接的方式得到由軸線組成的扇形區,再對該區域進行搜索得到最佳路徑。由此實現穩定運行與快速搜索的目的,可以更好地適應艦船導航中的復雜網絡環境。
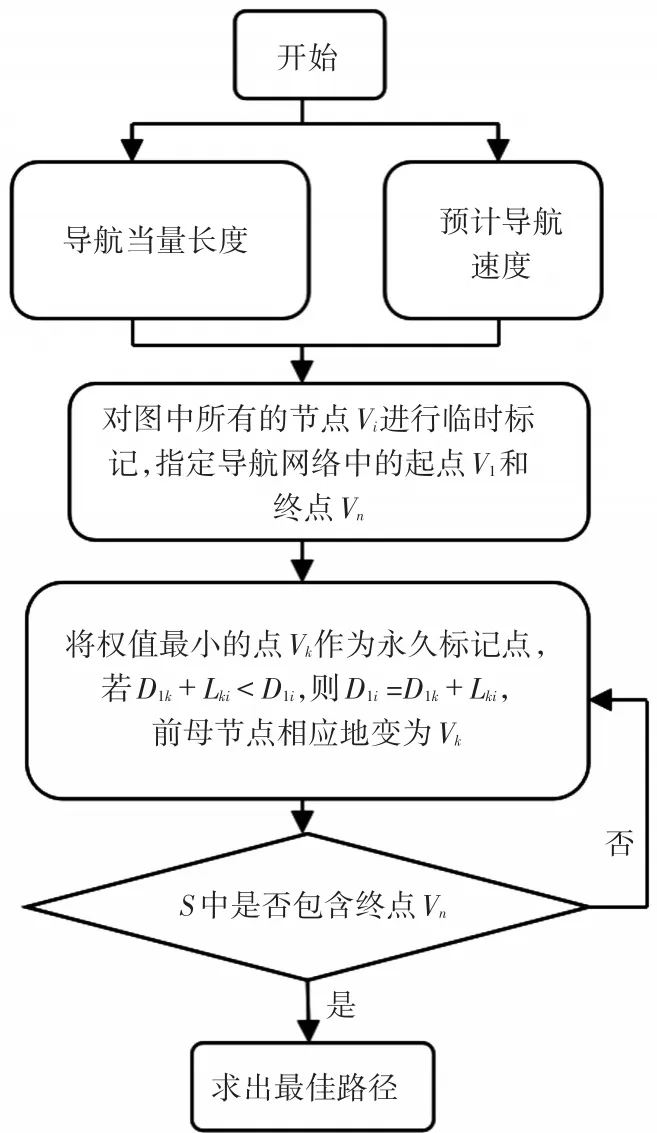
圖1 Dijkstra算法流程圖
從圖1中可以看到采用扇形優化Dijkstra算法進行分析的流程,具體步驟如下:
1)從艦船導航網絡內選擇出起點V1以及終點Vn,在此基礎上求得最佳扇形區;
2)臨時標記圖中的各個起點Vi,分別以二個坐標來表示各節點,其中,第一個坐標是節點對應的母節點,即與最佳路徑相鄰的之前節點,第二個坐標對應的是此節點與起點V1之間的距離權值;把V1標記成(1,0),再以(1,D1i)來表示其它節點Vi,若果Vi與V1之間是保持直接相連的狀態,則可以得到D1i=L1i,如果Vi與V1之間不是保持直接相連的狀態,則此時D1i=∞,同時將V1歸入永久標記點組成的集合S={V1};
3)對比分析集合T=V-S內各個沒有被標記的點對應的權值選,從中選出具有最小權值的點Vk作為永久標記點,此時可以得到S={V1,Vk},和永久標記點Vk之間保持直接相鄰狀態的各個點Vi,當滿足條件 D1k+Lki<D1i時,存在 D1i=D1k+Lki,此時母節點將轉變成Vk;
4)重復執行以上各個步驟到終點Vn為止,得到的D1n是最優路徑權值和,由終點母節點往回追溯,便可得到這一最優路徑。
4 應用示例
從圖2中可以看到對艦船的局部導航進行模擬所得的網絡,可以發現節點①代表航船的實際位置,節點⑨是導航目標位置。求解由節點①與節點⑨之間的最佳路徑,確保這一路徑是各個可行路徑中能夠實現最佳通行時間的導航。
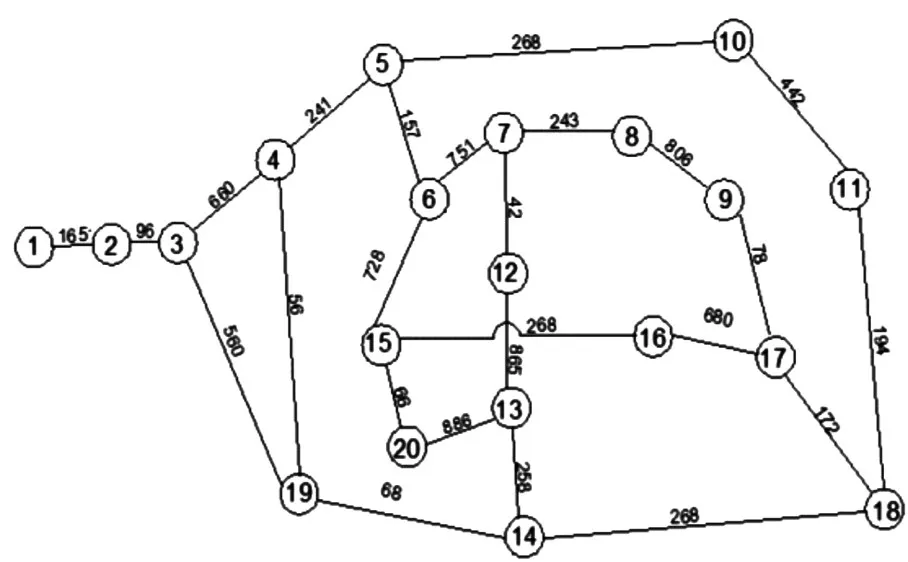
圖2 艦船局部導航模擬網絡圖
為海上作業人員提供的啟動后根據實際型號的差異實際可用時間介于25min~40min范圍內。因此,海上作業人員需確保能在的有效工作時間中導航到安全的避難位置。根據以上分析,本文將有效時間設定為25min,相當于所有作業人員到達最近安全區域的時間不能超過25min。
針對本模型艦船的真實情況,分別為節點3與節點6,并以此作為人員導航的安全目標位置。而且給其他各個節點人員到節點13需要的時間都大于25min,所以其他各節點的海上作業人員應在限定時間內轉移至別的安全位置點。
可以作為導航安全位置的節點包括節點3、6、13與17,之后再通過Dijkstra算法求解出從艦船模型內的各節點導航至上述安全位置點需要消耗的時間以及尋找最佳導航路徑。從表1中可以看到由本文艦船模型的20個節點導航至節點3、6、13與17對應的時間。
表2是根據海上局部導航圖各參數進行計算所得的結果,可以看到每次搜素時得到的最小導航當量。其中,最佳導航路徑是①②⑤⑧⑨。
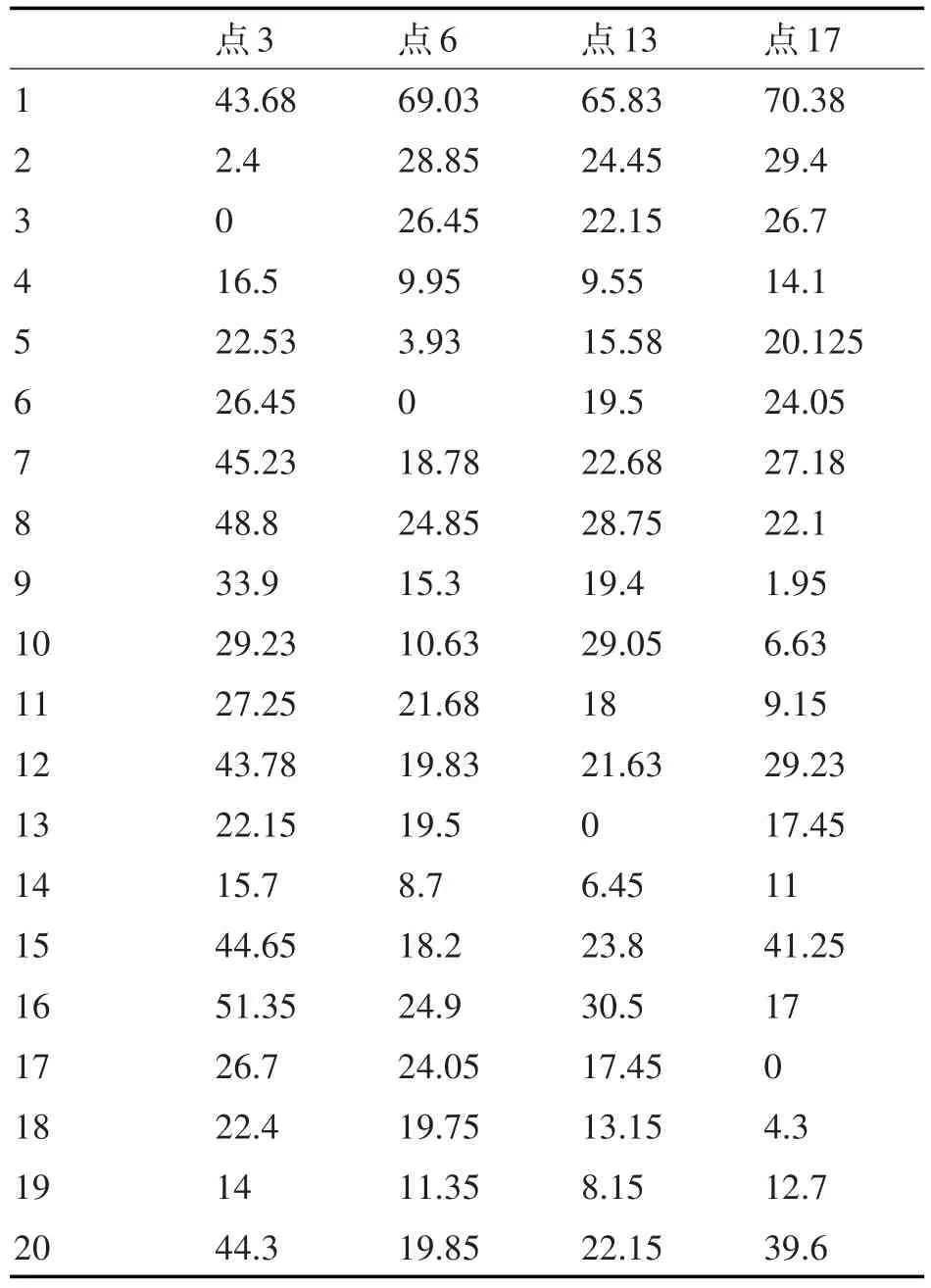
表1 節點導航時間表
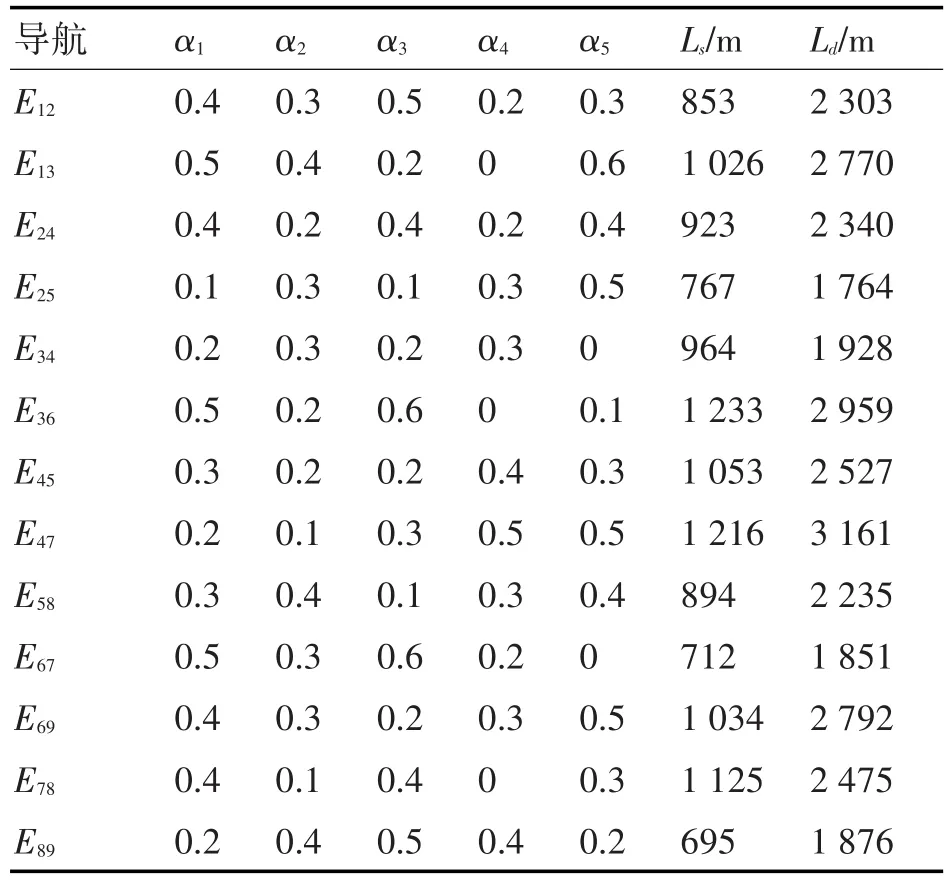
表2 導航參數表
基于Dijkstra算法得到的K則最優路徑雙向搜索算法可以得到多條最佳導航路徑,本文選擇其中的兩種最佳導航路徑,結果見表3。
根據表3可知,當出現安全事故時,作業人員可通過最近安全避難點進行導航。
選擇VSL進行最佳路徑編程并演示海上導航培訓系統運行過程,其中該程序的腳本圖可以讀取導航當量長度與人員導航速度,同時根據Dijkstra算法求出最佳導航路徑,形象展示導航過程。

表3 最佳導航路徑表
先在Virtools內創建VSL腳本程序,如果發現腳本圖內存在不同的VSL腳本程序時則對其進行更名,從而準確分辨各VSL腳本程序的功能。再結合實際需求設定bIn/bOut端口與pIn/pOut參數的種類與數量。
先通過VSL腳本程序創建得到一個存儲表來保存當量長度與導航速度。創建Run VSL并將其更名為Laneway Data Array,再把存儲導航參數的代碼輸入編程欄進行調試。
之后,以VSL腳本程序進行編程并求解出最佳路徑,構建一個Run VSL并將其更名為Get Shortest Path。選擇VSL來編寫Dijkstra算法時,通過優化改進處理可以降低搜索過程的遍歷節點個數,使程序高效運行。
最后,以系統BB模塊依次和通過VSL腳本程序編譯的Laneway Data Array模塊以及Get Shortest Path模塊進行連線得到腳本圖。
在系統的操作界面中,點擊選擇系統的演示功能,從圖2選擇節點①作為受災位置,再點擊系統的演示按鈕,可以看到此時系統的人物開始演示導航的過程,并可以得到導航所需的最佳路徑及時間。
根據本實驗測試結果可知,利用VSL編程以及把Dijkstra算法應用于海上導航模擬系統是完全可行的。
5 結語
對導航當量長度以及導航速度進行了深入探討,給出了扇形優化Dijkstra算法進行分析流程,并進行了應用示例。研究結果得到:
1)基于Dijkstra算法得到的K則最優路徑雙向搜索算法可以得到多條最佳導航路徑,本文選擇其中的兩種最佳導航路徑,完全滿足避難需求。
2)選擇VSL進行最佳路徑編程并演示海上導航培訓系統運行過程,根據Dijkstra算法求出最佳導航路徑,形象展示導航過程。利用VSL編程以及把Dijkstra算法應用于海上導航模擬系統是完全可行的。

