細尾礦砂非飽和滲流穩態含水率二維解析解*

林雪松, 王永吉, 王 東, 王來貴, 王漢勍, 宋澤友, 王中東, 李俊岑, 馮 歡

(1.遼寧工程技術大學 理學院，遼寧 阜新 123000; 2.阜新高等專科學校，遼寧 阜新 123000;3.遼寧工程技術大學 力學與工程學院，遼寧 阜新 123000)

0 引言

尾礦壩一旦發生潰壩將對下游人民的生命安全和生存環境造成嚴重破壞[1]，因此一直以來都是安全生產領域的重點研究內容。近年來，由于尾礦顆粒越來越細[2]，固結越來越困難，壩體潰決概率出現了不斷上升的趨勢，使得針對細尾礦砂堆筑的尾礦壩的研究開始吸引學者們的注意[3-4]。水的分布狀態是影響尾礦壩安全的重要因素，細尾礦砂堆筑的尾礦壩更是如此。尾礦壩中的水分有很大一部分是存在于非飽和尾礦砂中的，在尾礦壩的安全狀態評估中，必須考慮非飽和部分的影響[5]，而清楚地描述非飽和尾礦砂內部水分的分布狀況是考慮該部分影響的重要前提，必須進行深入探索。多年來國內外學者針對非飽和滲流問題進行過很多有意義的研究。張志軍等[6]通過尾礦砂室內毛細水上升測試發現：尾礦砂中毛細水的上升規律呈初期迅速而后期緩慢的變化趨勢，是其受多種作用力的共同作用所致;魏樣等[7]通過室內土柱試驗發現：不同土質的污染土壤內，毛細水上升高度與時間均符合良好的冪函數關系;郝瑞等[8]利用自行設計的層狀土室內模型試驗監測了毛細水上升過程，通過試驗結果對LW模型進行了修正。前述工作可歸類為實驗方面的研究，在數值計算方面，Neuman[9]首先提出通過有限元方法解決二維飽和-非飽和滲流問題;湯卓等[10]基于非飽和土滲流理論建立了尾礦壩三維有限元模型，總結了上游法尾礦壩流固耦合計算規律；彭華等[11]對滲流問題的有限元分析方法加以改進，消除了非飽和滲流計算中存在的數值彌散現象，提高了收斂速度 ;王鐵行[12]給出了考慮含水率和密度影響的非飽和黃土路基水分場數值計算模型;劉杰等[13]研究了非飽和土路基毛細作用的數值與解析方法;李毅等[14]運用變單元滲透系數法，通過FLAC3D的二次開發得到了飽和-非飽和滲流場;王睿等[15]通過引入時間分數階導數，結合2種水力傳導系數對新的Richards方程進行了數值求解。

縱上發現，前人在非飽和滲流問題的實驗和數值計算方面進行了大量研究，但較少見到解析方法方面的研究，即便使用解析方法也僅限于處理一維問題。實驗和數值計算當然是探討非飽和滲流問題的有效方法，應該投入精力進行研究與發展，但重視實驗和數值方法的同時也應該重視解析方法，加之尾礦壩問題通常涉及2個維度，因此對二維問題的解析研究意義也同樣明顯。

本文擬從非飽和滲流的Richards方程出發，在對求解區域和邊界進行適當加工的基礎上，得到尾礦砂二維非飽和滲流的穩態解析解，然后通過得到的解析解擬合細尾礦砂實驗數據，觀察解的擬合效果。主要目的是通過研究給出符合實際的非飽和細尾礦砂內含水率分布計算的思路與方法，為考慮非飽和部分的尾礦壩安全評估工作提供基礎資料。

1 創建解析模型

Richards方程是細尾礦砂非飽和滲流所涉及的基本方程，若以體積含水率θ為待求解函數，坐標系的z軸以豎直向上為正，三維問題中的Richards方程的形式如式(1)所示[16]。方程中的D(θ)稱為擴散系數，D(θ)隨θ的變化而變化，因此表達為函數形式；K(θ)表示非飽和尾礦砂中水分的滲透系數，也表達成了θ的函數。在尾礦壩工程中通常研究的都是二維問題，此情況下，如將坐標軸y以豎直向上為正方向，且僅僅研究穩態問題不討論瞬態問題，式(1)可變化為式(2)。雖然式(2)的形式已經比較簡單，但若想求得解析解尚需在符合實際的基礎上繼續簡化。接下來將D(θ)取為常數D，則式(2)又可化為式(3)。

(1)

(2)

(3)

需要指出的是，將D(θ)取為常數D并不是認為實際中D(θ)一定為常數，而是在運算中用某種平均值來代替D(θ)，前人曾實踐過類似的簡化思路[13]。式(3)必須和一定的求解區域和邊界條件聯系在一起才能求解，若區域的形狀太過復雜是無法得到解析解的，因此應當將求解區域選為簡單形狀，在接下來的研究中，選擇矩形求解區域，因為矩形區域內的方程求解是完全可以做到的，且實際中很多工程問題的求解也可歸結到矩形區域內。接下來考慮式(3)的邊界條件。通過對已有實驗結果(論文后面會給出)的分析可看出，含水率在豎直和水平方向上都近似遵循指數變化的規律，有鑒于此，在矩形的求解區域內，建立式(4)～(6)所示的方程和邊界條件。

(4)

θ|x=0=ae-byθ|x=q=ce-dy

(5)

θ|y=0=fe-gxθ|y=h=je-kx

(6)

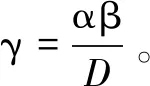
2 求解模型的具體過程

方程和邊界條件建立起來之后，就涉及到求解整個模型。首先，方程和邊界條件都是非齊次的，可對邊界條件先進行齊次化處理。令含水率θ=w+v，w和v為2個待定函數。假設v滿足邊界條件(5)，且令v=Ax+B，A和B同樣為2個待定函數。將v帶入邊界條件(5)解得：

(7)

從v的表達式中可看出：

(8)

將θ=w+v及v的表達式帶入方程和邊界條件(4)～(6)得到關于w的方程和邊界條件如式(9)～(11)所示：

(9)

w|x=0=0，w|x=q=0

(10)

(11)

利用分離變量和傅立葉級數法可得到w的表達式為：

(12)

公式中Cn，Dn的形式為：

(13)

(14)

則最終得到含水率空間分布的表達式為：

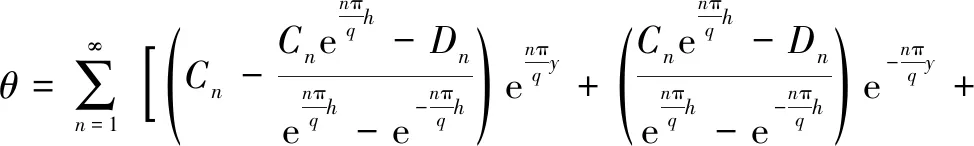
(15)

很明顯最終的結果具有無窮級數形式，但由于系數都具有很強的收斂性，所以在實際中只取其中前幾項就足夠了。

3 基于實驗結果的模型效果檢驗

3.1 實驗設計與結果

1)實驗裝置與物料

主要實驗裝置如圖1所示，包括儲水腔室(1 m×0.1 m×1 m)和儲料腔室(0.1 m×0.1 m×1 m)，尾礦物料全部放置在儲料腔室內，圖1中儲料腔室上的格點表示計劃測含水率的位置。儲水腔室用于提供滲流過程中所需的水，2個腔室之間的隔板上設置有鉆孔，用來保證滲流過程中水供應的順暢。實驗對象為某鐵礦尾礦砂，顆粒組成見表1，表1中數據顯示：50%以上顆粒粒徑小于0.019 mm，大于0.074 mm的顆粒含量低于10%，大于0.037 mm的顆粒含量低于30%，實驗用尾礦砂完全可歸類于細尾礦砂[17-18]。或者按照工程分類方式歸類為尾黏土。

2)實驗主要過程與參數設定

在實驗開始之前，先將尾礦砂填筑到儲料腔室內，然后在儲水腔室中注入清水，當腔室內水位達到0.05 m時停止注水，并通過虹吸方式使水位保持恒定。接下來細尾礦砂開始在恒定水源水位的基礎上進行飽-非飽和滲流。實驗中潤鋒的位置與形態不斷發生變化，當潤鋒完全穩定時認為實驗結束。細尾礦砂滲流速度較慢，從實驗開始到潤鋒穩定共計用了2個月時間。剛開始水平向滲流速度大于豎直向滲流速度很多，但隨著滲流的發展二者差距越來越小。穩定后的狀態如圖1所示，圖1中AA′表示穩定后的潤鋒，BB′表示實驗中尾礦砂試件內出現的1個裂縫。滲流達到穩態后對儲料腔室上標記的各格點進行挖掘，利用烘干法測含水率。該細尾礦砂飽和狀態體積含水率為49.80%。

表1 細粒尾礦砂粒徑組成Table 1 Composition of particle size of fine tailing sand

圖1 實驗結果Fig.1 Experimental results

3)實驗結果

測量得到的豎直向含水率分布曲線如圖2所示，水平向含水率分布曲線如圖3中的實測值所示。由圖2～3可知：無論豎直還是水平方向，含水率均逐漸降低，降低趨勢具明顯的非線性，可近似用指數函數描述。鑒于曲線的分布特點，前述模型中的邊界條件均采用指數形式。

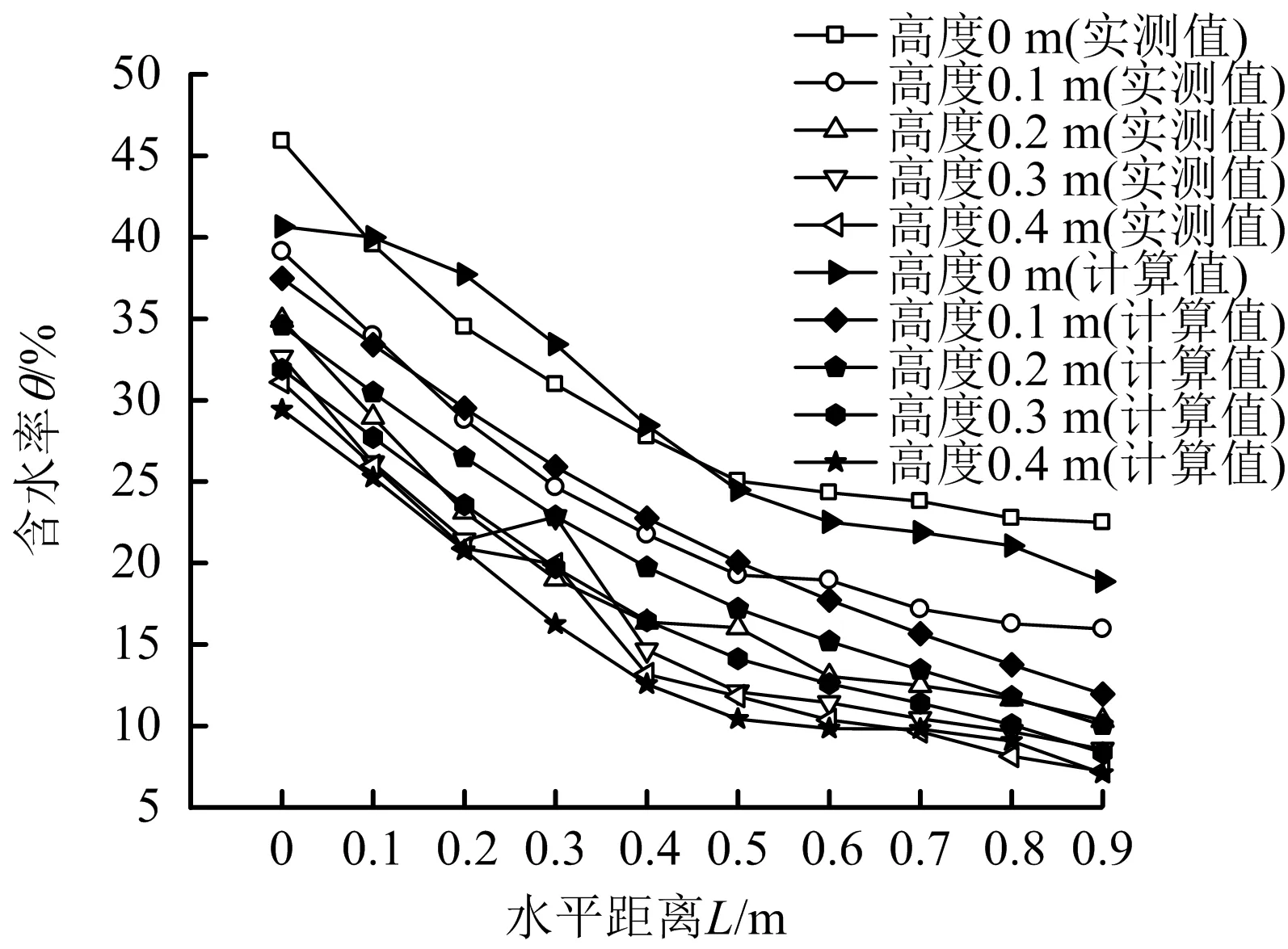
圖3 水平向含水率分布Fig.3 Horizontal distribution of water content

3.2 模型參數的確定

前述解析解(15)中包含共計10個未知參數，未知參數完全可利用實驗數據通過數學方法得出。可選的數學方法有很多，通過仔細調研，最終決定采用混沌粒子群優化算法(Chaos Particle Swarm Optimization，CPSO)來計算參數。由于理論公式只能應用在矩形區域內，因此應用公式的時候首先需要構造矩形域。

為檢驗計算得到的參數對所有數據的預測結果如何，需將由理論模型計算得到的各點含水率與實際測量結果進行比較，接下來展示出不同高度處含水率沿水平方向分布的實測值和理論值，以此將所有測量點處的實際測量值與理論計算值進行比較。比較結果如圖3所示。如果仔細觀察圖3可看出，在高度0.1，0.3和0.4 m處，實測值與計算值符合的比較好，在高度0和0.2 m處，數據擬合結果相對要稍差一些，但相差的也不是很大，總體來說，模型計算值和實測值是比較接近的，證明了用推導出的公式來描述實驗數據是完全可行的。因此解析解可被認為是含水率空間分布的理論規律，計算得到的分布曲線一般是要比測量得到的曲線稍顯平滑。

3.3 擬合結果

針對3.1節實驗構造的矩形域如圖1中的COEF所示，在矩形域上分別建立了x軸和y軸，矩形域內共計包含了50個數據點，可用來擬合參數。運算中在參考試算經驗的基礎上，將最大迭代次數設置為1 000，迭代過程中誤差的變化如圖4所示，從圖4中看到，開始的時候收斂速度比較快，然后收斂速度逐漸變慢，隨著迭代次數的增加最后誤差趨于恒定值。由計算得到公式中的未知參數取值如下：

α=6.839 088 379,β=20 000.0,a=44.229 302 31,b=0.096 026 944 5,c=979.961 319 9,d=20 000.0，f=4 465.811 49,g=0.120 477 598 5,j=21.483 476 85,k=16 768.464 75,D=16 177.809 65。

圖4 誤差變化Fig.4 Error development

4 結論

1)通過解析方法得到了描述非飽和尾礦砂含水率空間分布的公式，求解過程表明，細尾礦砂非飽和滲流穩態問題的解析求解可以從Richards方程的簡化開始，簡化主要沿著2個方向，第1是將方程形式簡化，簡化過程中包括降低維度，變瞬態為穩態，將未知參數簡化為常數或固定函數形式等；第2是將復雜求解區域簡化為矩形，在矩形區域里只要給出合適的邊界條件是可以得到方程解析解的。

2)模型求解所需的邊界條件可在參考實驗數據的基礎上給出，以此來保證求解結果的有效性。簡化過程中引入的參數可通過CPSO算法編制程序利用測量數據得出。算法計算中誤差具有明顯的收斂性。得出的參數能夠很好地擬合全部測量數據。由計算得到的曲線較實測曲線具有明顯的光滑性。