基于化學元素與化學鍵的無向化學鍵網動態研究

劉潤瞻 張寧

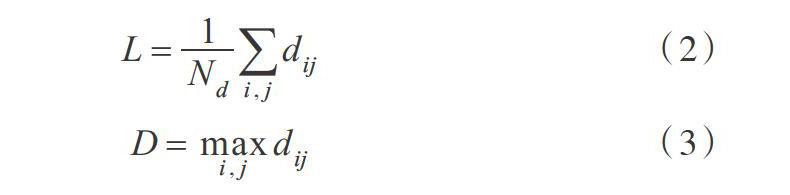
摘 要：為分析無向化學鍵網絡拓撲結構隨時間變化的動態演化規律，從4 274個二元化合物中提取97個化學元素和2 198個化學鍵，搭建無向化學鍵網絡;利用元素發現時間，搭建對應演化網絡。研究表明，演化網絡規模隨時間變化穩定增加，網絡密度、平均度、平均路徑長度等指標隨時間變化在固定值上下波動。部分參數變化的轉折點一定程度上反映了人類科技發展的變化情況。演化網絡研究可反映該無向網絡拓撲結構的動態穩定性，證明了化學元素—化學鍵系統的復雜性與特殊性。

關鍵詞：化學元素;化學鍵;無向化學鍵網;動態演化規律

DOI：10. 11907/rjdk. 182550

中圖分類號：TP319文獻標識碼：A文章編號：1672-7800（2019）001-0157-05

Abstract： To analyze dynamic evolution laws of structure of the undirected chemical bond network with time， this paper extracts 97 chemical elements and 2 198 chemical bonds from the data of 4 274 binary compounds to build the undirected chemical bond network， and collects discovery time of elements to build the corresponding evolution network. This research shows that the scale of the evolution network increases steadily with time increasing， while its topological parameters fluctuates at a fixed value， such as network density， average degree and average path length. Turning points of changing trends of some parameters reflects the changes of development in human science and technology to some extent. Research of the evolution network reflects the dynamic stability of the undirected chemical bond network and shows the complexity and specificity of the chemical element-chemical bond system.

0 引言

1998年興起的復雜網絡作為統計物理學和系統科學的一個分支，是一門基于圖論的研究客體之間關系的學科。該學科能夠定性和定量地描述客體之間的關系，被廣泛應用于計算機科學、社會科學等領域[1-6]。在化學領域，復雜網絡的應用主要依賴于化學反應方程式和化合物的組成[7-11]。如王博川、Gunawardena等[7-9]以化學反應方程式中的反應物和生成物為對象、以同在一個方程式中為關系，構建網絡進行復雜網絡應用研究。Estrada以礦物質組成元素為對象、以同在一個礦物質中為關系構建網絡[10]。Leal等[11]以二元化合物的組成元素為對象、以同在一個形如[AmBn]的二元化合物為關系構建網絡進行研究。

在化學元素的復雜網絡應用研究中，Estrada[10]認為所有化合物組成元素間均存在關系，利用二分網和無向網絡的相關方法進行研究;而Leal等[11]僅利用二元化合物搭建網絡，連邊以及整個網絡的化學意義并不明顯。本文在前人基礎上，引入化學鍵進行研究。忽略化學鍵數量和類型，假定對于元素[A]和元素[B]，如果兩者之間存在穩定的化學鍵，則兩元素對應的網絡節點有且僅有一條連邊連接，由此構建無向化學鍵網絡。故在該網絡中，每一條邊都對應于能夠穩定存在的化學鍵，使網絡能表達的化學意義更豐富。

為具體分析該網絡拓撲結構演化規律，引入元素和化學鍵發現時間，作為節點和連邊加入至網絡時間點，分析以時間點先后順序構成的網絡拓撲結構演化過程，著重研究參數演化趨勢及其與對應時期生產力、科技水平變化情況之間的關系。

1 化學元素發現時間

一般情況下，只有在某一特定元素被發現后，才能檢測與分析該元素可形成的化學鍵，被大規模地用于合成、研究與該元素相關的化合物。為簡化研究難度，本文忽略化學鍵具體發現時間，僅以元素發現時間作為化學鍵發現時間。因此，只有當一個節點對應元素的發現時間小于或等于給定時間點，且一條邊的兩個元素發現時間均小于或等于給定時間點時，該節點和邊才被認為存在于對應時間點的網絡中。不區分同一年被發現的元素先后順序，均被認為是同時加入網絡的。

由于研究條件和研究資源限制，難以獲取化學鍵數據。而一般認為，只要一個二元化合物被確認能夠穩定存在，則該化合物組成元素間一定存在化學鍵。因此可利用二元化合物數據作為一種近似的化學鍵數據進行分析研究。本文利用文獻[12-17]記錄的二元化合物數據抽取得到化學鍵數據，構建無向化學鍵網絡，再利用文獻[12]中元素發現時間作為元素對應節點和邊，加入該無向化學鍵網絡的時間，生成不同時間點的無向化學鍵網絡，利用常用復雜網絡指標對網絡拓撲結構進行動態分析。

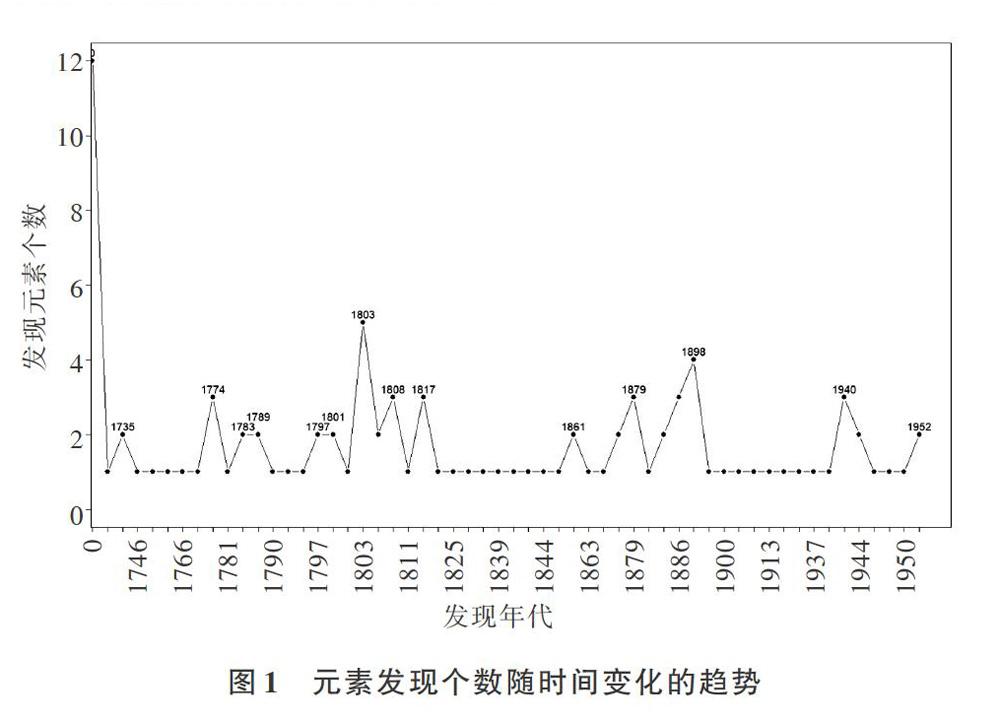
搜集文獻[12-17]，得到4 274個二元化合物，涉及97個化學元素和2 198個化學鍵。搜集文獻[12]中97個化學元素對應的發現時間，發現碳（C）、硫（S）、銅（Cu）、汞（Hg）等12個元素的發現時間在公元前，具體年代不詳，假定為初始值0。為分析化學元素發現個數與對應時間的關系，本文根據元素被發現的時間先后順序繪制對應發現元素個數的變化趨勢，如圖1所示。

從圖1中可以發現一共有56個時間點，最小值為初始值0，最大值為1952年（對應元素為锿和鐨）。除初始值0外，發現元素最多的年份是1803年和1898年，分別有5個和4個。在圖1中，出現峰值的時間點一般略遲于新化學技術和理論被應用與研究的時間點，如1783年法國化學家拉瓦錫提出燃燒的氧化學說、1800年意大利物理學家伏特發明伏達電堆（英國化學家戴維等由此通過電解化合物發現鈉等化學元素）、1803年英國化學家道爾頓提出原子論理論、1859年德國科學家本生和基爾霍夫提出光譜分析法并制造光譜分析儀（導致銫、銣等元素的發現）、1895年德國物理學家倫琴發現X射線（后人對放射現象進行深入研究，最終發現鈾、鐳等放射性元素）等，一定程度上反映了對應時代科學技術水平的變化情況[18-19]。

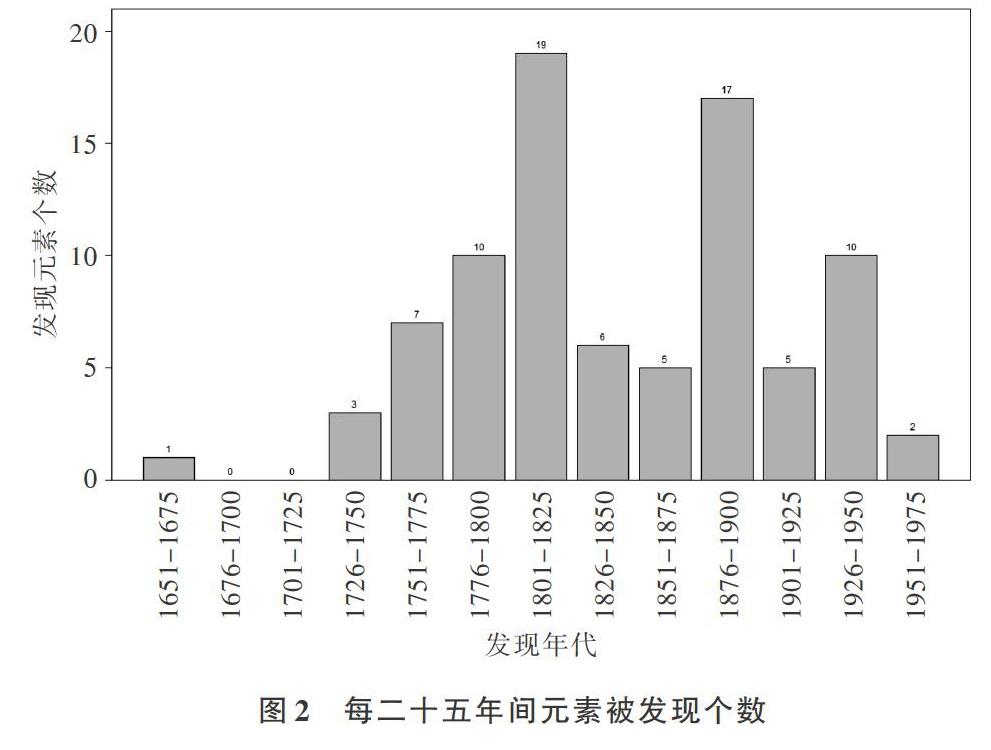
以25年為時間間隔，統計自1651-1975年間各階段發現的元素數量，見圖2。分析發現，尖峰出現4次，分別為1651-1675年、1801-1825年、1876-1900年、1926-1950年，對應于文藝復興時期（14-17世紀）、第一次工業革命（18世紀60年代至19世紀40年代）、第二次工業革命（19世紀70年代至20世紀初）和第三次工業革命（20世紀40、50年代以來），一定程度上反映了相應時代科技和生產力發展水平的變化情況[18-19]。

2 網絡參數動態演化過程

2.1 網絡基本參數與參數變化趨勢

如果一個無向網絡的節點數為[N]、邊數為[M]，則網絡密度[ρ]定義為網絡中實際存在的邊數[M]與最大可能的邊數之比，見公式（1）[20-21]。對于任意節點[i]，其度[ki]定義為與節點[i]直接相連的邊數目，故該網絡平均度定義為網絡中所有節點度的平均值[20-21]。網絡密度和平均度大小可反映該網絡拓撲結構稀疏程度。

在無向網絡中，節點對[（i，j）]的最短路徑定義為連接兩個節點最少的邊集合，距離[dij]定義為最短路徑對應邊數;如果這樣的集合不存在，即節點對[（i，j）]之間不連通，則距離[dij]定義為無窮大。假定網絡中所有聯通節點對個數為[Nd]，網絡平均路徑長度[L]定義為網絡中所有連通節點對之間距離平均值，見公式（2）[20-21]。網絡中任意兩個可達節點間距離最大值定義為網絡直徑[D]，見公式（3）[20-21]。平均路徑長度和直徑大小可衡量該網絡拓撲結構緊密程度。

以發現時間為1952年的無向化學鍵網絡為例，本文統計了網絡中所有97個元素對應節點度值，并與元素Pauling電負度值進行比較（數據來源于文獻[12]），依元素原子序數排布繪制出對應的變化趨勢，見圖3。發現兩者呈現出相似的周期性變化規律，反映該網絡連邊是有選擇的、且不服從冪律分布，說明了拓撲結構演化具有周期性與特殊性規律。為量化分析這種相似性變化情況，本文通過元素對應節點的度與其Pauling電負度之間的相關性和顯著性分析，探索相關系數與檢驗p值隨時間變化的趨勢。

研究發現該網絡在任意時刻都是一個全連通圖，即網絡中任意兩個節點都是連通的。統計所有無向化學鍵網絡節點數和邊數，依演化順序繪制對應的變化趨勢圖，見圖4。忽略發現時間之間年代差的不同，可以發現該網絡節點數和邊數隨年代發展呈現出較強線性增加趨勢（擬合優度[R2]均大于0.98），從初始時刻節點數最小值12、邊數最小值41，穩定增加至1952年節點數最大值97、邊數最大值2 198。

對不同時間點下的網絡密度、平均度、平均路徑長度、網絡直徑以及Pearson相關系數和檢驗p值等基本參數進行計算，依時間順序繪制變化趨勢圖，見圖5。發現雖然該網絡規模呈穩定增長趨勢，平均度也呈先增加再趨于穩定的趨勢，但網絡密度、Pearson相關系數及平均路徑長度變化趨勢的方差均小于0.1，檢驗p值較快地趨于0（對應時間點為1807年），網絡直徑也從2增加至3，反映了該網絡拓撲結構具有動態穩定性。

平均度與網絡直徑變化趨勢轉折點均在1886年，可能是由于后期發現的元素主要是零族、稀土以及放射性元素等[18-19]。這些元素自身特性使對應化學鍵數據難以獲取，網絡邊數沒有隨節點數的增加而大幅增加，最終導致網絡結構出現較大改變。

網絡密度呈現出先增加再減小的趨勢，而平均路徑長度呈先減小再增加的趨勢，兩者的轉折點均出現在1774年、1802年、1808年、1842年和1886年，對應于文獻[19]所述的古典化學分析時期（1771-1800）、電化學時期（1801-1830）、光譜分析時期（1861-1900），也與第一次工業革命（18世紀60年代至19世紀40年代）、第二次工業革命（19世紀70年代至20世紀初）的時間吻合。說明該網絡拓撲結構動態演化趨勢可反映對應時期的科技水平與生產力發展水平。

2.2 聚類系數與同配系數

網絡聚類系數大小也從另一個方面反映該網絡拓撲結構緊密程度。對于無向網絡，如果節點[i]的所有一階鄰居個數為[Ni]，則節點[i]的聚類系數[Ci]定義為該節點一階鄰居（即所有與該節點直接相連的節點）間所有實際相連的邊數[Ei]除以一階鄰居間所有可能的最大連邊數[Emaxi]，見公式（4）[22]。網絡聚類系數[C]定義為所有節點聚類系數[Ci]的平均值[22]。

X在一個網絡中，節點間是否有邊連接與該節點度值有關，則同配系數被用于定性和定量衡量網絡中度值大的節點間連接傾向程度。本文利用基于Pearson相關系數定義的同配系數對該網絡同配性進行定量分析，見公式（5）[22-24]。

當[r>0]時，說明該網絡具有同配性，反映網絡中度值大的節點更傾向于與度值大的節點連接;當[r<0]時，說明該網絡具有異配性，反映網絡中度值大的節點更傾向于與度值小的節點連接[22-24]。[r]的大小則反映網絡同配性或異配性強弱，可用于比較不同規模網絡間性質差異程度。

利用公式（4）分別計算不同時間點對應網絡聚類系數，繪制聚類系數變化趨勢，見圖6。通過計算發現，該網絡變化趨勢平均值為0.769 7、方差為0.002 2，自1901年起在固定值0.705 0處波動變化，反映該網絡結構穩定性。其趨勢變化轉折點在1669年、1755年、1774年、1808年、1826年和1901年，基本對應于不同時期生產力發展水平和科技水平變化情況[18]。此外還發現該網絡在任意時間點上同時具有較小的平均路徑長度、較小的網絡直徑和較大的聚類系數，因此認為其具有不隨時間變化的小世界特性[22]。

利用公式（5）分別計算不同時間點對應網絡的同配系數，繪制對應的變化趨勢圖，見圖6。通過計算發現，該網絡在任意時間點上的同配系數均小于0，說明該網絡始終具有異配性，一定程度上反映了網絡開放性[22]。其變化趨勢平均值為-0.230 3、方差為0.004 0，同樣體現出網絡結構穩定性。該趨勢變化轉折點位于1746年、1755年、1781年、1803年、1826年、1875年、1898年和1939年，自1875年后呈波動下降趨勢，同樣能夠反映不同時期生產力發展水平和科技水平變化情況[18-19]。

2.3 參數變化趨勢相關性分析

如果把化學元素和化學鍵看成是一個系統（化學元素—化學鍵系統），化學元素作為系統客體，化學鍵作為客體之間的關系，則對無向化學鍵網的動態研究可看作是從復雜網絡角度對該系統進行的動態演化研究。從圖4-圖6可發現隨著網絡規模的線性增長，部分指標呈現出在固定值附近波動的變化趨勢，網絡性質沒有較大改變，反映了該化學元素—化學鍵系統結構穩定性。網絡密度、網絡平均路徑長度、網絡直徑等指標之間的變化趨勢也呈現出相似變化規律。對隨時間變化的Pearson相關系數進行計算，見表1，分析參數間內在關聯。

通過表1可以發現，除同配系數與平均度外，參數間相關系數絕對值均大于0.5，大部分指標結果的絕對值大于0.75，反映了該網絡拓撲結構的不同參數在時間演化規律上呈現出較強相關性，說明該網絡拓撲結構時間演化規律及對應“化學元素—化學鍵”系統的復雜性與特殊性。

3 結語

本文將元素發現時間作為網絡演化的時間點，分析無向化學鍵網拓撲結構隨時間變化而展現出的動態變化規律，研究趨勢轉折點與對應時期生產力和科技水平變化情況之間的關聯性，分析其化學元素—化學鍵系統演化特性。通過變化趨勢的研究，本文得出如下結論：

（1）該網絡規模隨時間演化呈現出穩定增長的趨勢。節點數、邊數變化趨勢符合線性增長的規律，平均度變化趨勢呈現先線性增加、再趨于穩定的規律，反映了網絡規模穩定增長的趨勢。

（2）該網絡拓撲結構隨時間演化呈現出較強的穩定性。網絡密度、平均路徑長度、同配系數等指標在固定值附近變動，反映了該網絡始終呈現出小世界、異配性的結構特性，說明了系統演化穩定性。變動轉折點一定程度上反映了對應時期生產力和科技水平變化情況。

（3）1807年以后，網絡中元素對應節點的度隨元素原子序數呈現出周期性變化趨勢，與對應元素電負性值呈較強的正相關性。

（4）部分指標趨勢之間的強相關性反映了網絡拓撲結構演化規律復雜性與特殊性，說明對應的化學元素—化學鍵系統具有復雜性與特殊性。

本文為從復雜網絡角度進行研究，為研究化學元素—化學鍵系統演化過程打下了基礎，對該系統的動態演化規律研究具有借鑒意義。化學鍵的引入使本文建網思路與動態研究思路體現出更為豐富的化學意義。但是由于條件限制，本文不能獲得所有已知化學鍵數據，只能從二元化合物數據中抽取出成鍵元素作為一種近似數據，因此下一步需要獲取更多的化學鍵和成鍵元素數據，進一步保證研究結果的準確性與價值，以便對該系統建立相應模型進行仿真與預測研究。

參考文獻：

[1] WATTS D J， STROGATZ S H. Collective dynamics of ‘small-world networks[J]. Nature， 1998， 393：440-442.

[2] BARABáSI A L， ALBERT R. Emergence of scaling in random networks[J]. Nature， 1999， 286：509-512.

[3] 張寧. 復雜網絡實證研究——中國教育網[J]. 系統工程學報， 2006（4）：337-340，409.

[4] 巴志超，李綱，朱世偉. 基于知識超網絡的科研合作行為實證研究和建模[J]. 情報學報，2016，35（6）：630-639.

[5] 張寧. 群體興趣網的統計特性研究[J]. 上海理工大學學報，2008（3）：243-248.

[6] 張晨， 張寧. 上海市公交網絡拓撲性質研究[J]. 上海理工大學學報， 2006（5）：489-494.

[7] 王博川. 化學反應網絡建網方式及統計性質初探[D]. 北京：北京師范大學， 2008.

[8] JEONG H， TOMBOR B， ALBERT R， et al. The large-scale organization of metabolic networks [J]. Nature，2000，407（6804）：651-654.

[9] SOLéAND R V，MUNTEANU A. The large-scale organization of chemical reaction networks in astrophysics[J]. Europhysics Letters， 2004，68（2）：170-176.

[10] ESTRADA E. The complex networks of earth minerals and chemical elements [J]. Match Communications in Mathematical & in Computer Chemistry， 2008， 59（3）：605-624.

[11] LEAL W， RESTREPO G， BERNAL A. A network study of chemical elements： from binary compounds to chemical trends [J]. Match Communications in Mathematical & in Computer Chemistry， 2012， 68（2）：417-442.

[12] ANOMITY. Web elements[EB/OL]. http：//www.webelements.com/.

[13] 日本化學會. 無機化合物合成手冊（第一卷）[M]. 曹慧民，包文滁，安家駒，譯. 北京：北京工業出版社， 1983.

[14] 日本化學會.無機化合物合成手冊（第二卷）[M]. 安家駒，陳之川，譯.? 北京：北京工業出版社，1983.

[15] 李夢龍. 元素化學反應速查手冊[M]. 第2版，北京：化學工業出版社， 2008.

[16] 張向宇. 實用化學手冊[M]. 北京：國防工業出版社， 2011.

[17] 中國科學院上海有機化學研究所.化學專業數據庫[DB/OL]. http：//www.organchem.csdb.cn.

[18] 王德勝. 化學元素發現史的統計分析[J]. 北京師范大學學報：自然科學版， 1983（2）：89-95.

[19] 應禮文. 新元素發現的編年表[J]. 化學教育，1983（1）：59+46.

[20] BIGGS N，LLOYD E，WILSON R. Graph theory，1736-1936[M]. Oxford： Clarendon Press，1976.

[21] DIESTEL R. Graph theory，graduate texts in mathematics[M]. New York： Springer，2016.

[22] 汪小帆，李翔，陳關榮. 網絡科學導論[M]. 北京：高等教育出版社，2012.

[23] NEWMAN M E J. The structure and function of complex networks [J]. SIAM Review， 2003， 45（2）：167-256.

[24] NEWMAN M E J. Assortative mixing in networks[J]. Physical Review Letters， 2002， 89（20）：208701.

（責任編輯：江 艷）