金融投資組合風(fēng)險調(diào)整研究

高鑫 張彩霞

（東北農(nóng)業(yè)大學(xué)經(jīng)濟管理學(xué)院，黑龍江 哈爾濱 150030）

引言

近年來，股票數(shù)量在投資組合中占比逐漸增加，針對投資組合的整體風(fēng)險研究也逐漸得到重視，而風(fēng)險價值是風(fēng)險控制的基礎(chǔ)。目前，大多數(shù)基金公司為了避免一些重大損失，會為每個交易者設(shè)定專屬的VaR金額限額，在防止過度交易的同時，VaR金額限額還可以進行基金業(yè)績評估。目前，大多數(shù)基金業(yè)績評價時不再單以收益水平為指標(biāo)，通過在業(yè)績評價中加入風(fēng)險因素，也能避免一些重大損失，防止投資者過度追求高收益高回報而忽視了投資風(fēng)險的防范。

一、VaR計算原理

假設(shè)在投資期間Δt期間投資組合的初始值為P0且收益率為R，則結(jié)束值為P = P0（1 + R）。則置信水平為c的投資組合的最小值為：

其中R*被為投資最低回報率。

相對VaR即相對于在產(chǎn)生投資組合最低值狀態(tài)時的風(fēng)險差異，其計算如下：

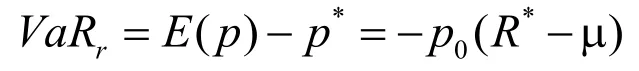
同時也可以計算相對于期初的最低值的風(fēng)險差，即絕對VaR：

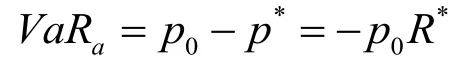
假設(shè)投資組合的年收益率是服從均值為μ和波動率為σ分布的隨機變量。則此時相對VaR可以表示為：

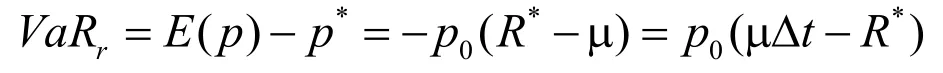
所以，只要求出在置信水平c下的R*或者P*，VaR計算就迎刃而解。

二、均值-VaR 組合優(yōu)化模型

在Markowitz的均值方差模型中，方差用于表征投資組合的風(fēng)險。本文在計算投資組合的風(fēng)險時，用VaR來代替方差，從而得到本文均值-VaR投資組合模型：

引入由均值 - 方差模型確定的有效邊界：

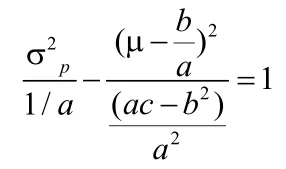
平均VaR模型的有效前沿方程：

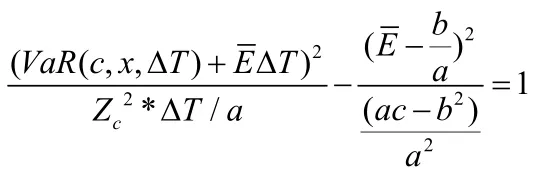
三、模型求解

在給定預(yù)期收益率時使得投資組合的VaR達到最小，是本文均值-VaR投資組合優(yōu)化模型的目標(biāo)，如果預(yù)期收益率不同，則會得到投資組合的不同有效前沿。本文利用樣本數(shù)據(jù)的歷史平均回報率來表示預(yù)期回報率，公式表述如下：

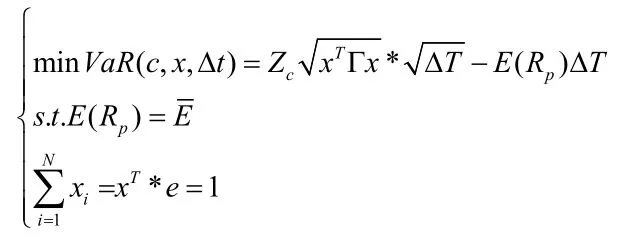
其中，E是給定的目標(biāo)期望收益率，最優(yōu)投資組合權(quán)重向量x和相應(yīng)的VaR可以根據(jù)給定的預(yù)期收益率獲得。結(jié)合歷史數(shù)據(jù)，E是我們給定的歷史收益率的平均值，也就是說設(shè)定了預(yù)期的收益率，Z c是正態(tài)分布的分位數(shù)95，計算結(jié)果VaR=2102512，得到平均VaR模型組合的有效前沿如圖1所示。

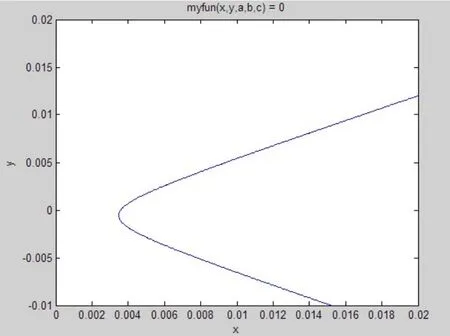
圖1 平均VaR模型組合有效前沿

四、結(jié)論

本文提出的均值-VaR模型在95%置信水平下，提出模型計算的VaR值與基礎(chǔ)VaR模型相比，投資組合風(fēng)險得到了有效降低，表明本文提出的均值-VaR模型可以降低投資組合的金融總體風(fēng)險水平。均值-VaR模型的有效前沿初值一般設(shè)為最小VaR組合點，投資者效用函數(shù)無須與其結(jié)合，具有更為一般的指導(dǎo)意義。