巧用游戲

陳國峰

1 教材分析

《幾何概型》是高中數學人教版必修三第三章第三節第一課時的內容，是普通高中在新課程改革的基礎上，新增的學習內容，可以看作是古典概型的推廣。它將古典概型的試驗結果從有限個拓廣到無限個，它是繼學生在了解和學習了隨機事件的概率以及古典概型之后，新引入的一類基本的概率模型，在概率論中有著十分重要的地位和作用。該部分的知識內容將事件發生的概率與構成事件區域的長度（面積或體積）成比例的模型，稱之為“幾何概型”。在新課程理念的驅動下，教師的教學實踐具有非常強的生動性和形象性，以更加有效地激發學生在具體的學習實踐中的參與意識，讓學生在對學習過程的具體而生動的參與體驗的過程中，實現對學習對象的有效理解和把握。幾何概型教學與游戲教學相結合，在教學設計的過程中，將幾何概型的特點、規律等與概率游戲有效地結合起來，讓學生在豐富而有趣的有效實踐中，更加直觀形象地獲得對游戲的豐富而生動的體驗過程，從而實現對學習對象的有效理解和把握。

2 教學目標

（1）在理解的基礎上掌握幾何概型的定義，并能夠初步識別簡單的幾何概型，準確求解概率。

（2）在具體的游戲參與實踐中，展開問題探究與實踐，通過對比、類比等方法，找到解決幾何概型問題的有效方案。

（3）培養學生用數學的眼光分析和看待生活中的問題的習慣，以科學的態度和方法去分析和評價身邊的隨機現象。培養學生科學的世界觀。

3 教學重難點

（1）重點：掌握幾何概型的判斷方法，以及幾何概型中概率的一般公式。

（2）難點：把實驗的基本事件和隨機事件與某一特定區域及其子區域對應，確定適當的幾何范圍，并在此過程中，學生的數學建模的有效構建。

4 教學過程

4.1 快問快答，點燃興趣

師：老師給大家三分鐘的時間回顧我們上節課學習的知識，時間到了，我們就開展快問快答游戲，每一個學生的口型必須跟上，才能夠在游戲中過關，大家準備好了嗎？

（1）古典概型的兩個特點。

（2）計算古典概型的公式。

4.2 情境創設，助力興趣

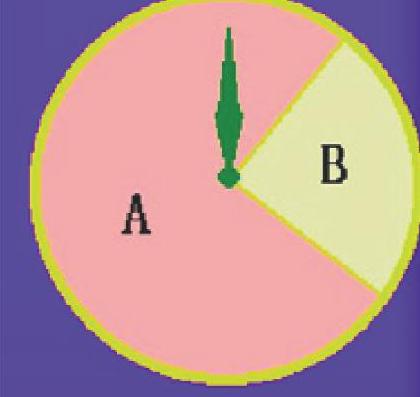
師：在生活中，我們常常會遇到結果有無窮多的情形，如一條線段或一個面上的任意一點，再如早上學生到校的時間是6：30——7：10之間的任何一個時刻.....，在具體的實驗中我們能夠發現，得到的結果是無限多個，而且這種新的發現要求我們在具體的學習過程中，通過一種新的方法來求解。首先我們來玩一個游戲，幸運大轉盤。

師：大家一邊玩一邊記錄下，在游戲過程中，誰勝利的的次數更多？

生：肯定是代表A區域的學生贏的次數多。

師：事實和大家估計得是否一致呢？

生：是的。

生：A獲勝的概率是3/4，由字母A所對應的扇形的面積和整個圓的面積之比是3/4.

師：為什么這樣比呢？

生：指針指向哪一個區域內的可能性是均等的，這可以作為基本事件，指針指向圓盤中的任何一個A區域內的范圍的事件為A，那么事件的發生的概率P（B）=3/4。

4.3 小組合作，知識建構

小組合作競賽，在緊張而有序的學習氛圍中，交流以下問題：

（1）幾何概型的定義

（2）幾何概型的特點

（3）幾何概型的計算公式

（4）幾何概型和古典概型的異同

A組：如果每個事件發生的概率只與構成該事件區域的長度（面積或體積）成比例，則稱這樣的概率模型為幾何模型，簡稱為幾何概型。

B組：（1）試驗中所有可能出現的結果即基本事件有無限多個。

（2）每個基本事件出現的可能性相等。

C組：P（A）=構成A事件的區域長度（面積或提及）/試驗的全部結果所構成的區域長度（面積或體積）

D組：古典概型與幾何概型的相同點即基本事件發生的等可能性。

E組：不同點是古典概型的基本事件個數的是有限的，而幾何概型的基本事件的個數是無限的;他們的求得的方法也是不同的，古典概型需要通過列舉法求得，而幾何概型則通過對區域內的幾何度量求得。

4.4 實踐應用，深化認識

（1）長度相關類型

某人午休醒來，發現表停了，他打開收音機，想通過電臺報時調表，求他等待的時間不多于10分鐘的概率。

（2）與面積有關的題型

在1萬km2的海域中有40km2的大陸架駐藏著石油，假如在海域中任意一點鉆探，鉆探到油層面的概率是多少？

（3）與角度相關德計算

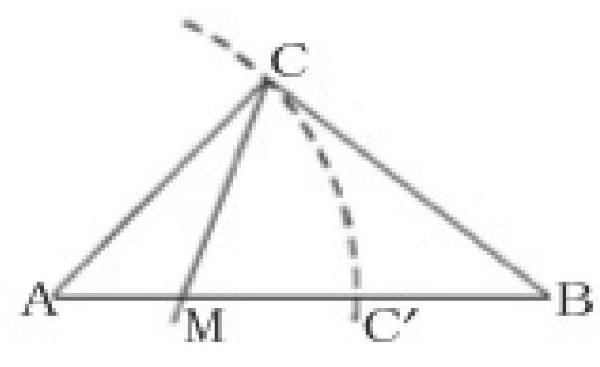
在等腰直角三角形ABC中，在斜邊AB上任取一點M，求AM的長小于AC的長的概率。

5 教學反思

5.1 用游戲點燃興趣的火焰

游戲教學法在高中數學教學實踐中的有效運用，能夠將復雜的知識簡單化、形象化，從而更加有助于學生的認識和理解體驗，在具體的教學設計的過程中，教師利用教學對象與游戲的關聯點，將知識性的元素創造性地加入到游戲的過程中，讓學生在輕松愉悅的游戲氛圍中，潛移默化地感受和體驗知識和理論在具體的實踐中的有效滲透，同時學生對數據的分析理解力、對數學知識的抽象能力以及數學建模等能力，在生動的游戲實踐中得到有效地建構。

第一環節的快問快答游戲，在游戲機制的驅動下，學生的思維和興趣能夠得到有效地調動，他們必然會因游戲本身的趣味性和競爭性而自主地行動起來，加上這部分的游戲考察的內容僅為簡單的記憶型問題，對學生來說沒有太大的難度，因而該游戲情境的創設能夠激發學生在具體的學習實踐中的有效記憶參與，促進學生對學習效果的高效理解和把握。

在第二環節的游戲過程中，將幾何概型教學的內容與轉盤游戲有機地結合起來，能夠有效地調動學生對游戲過程的參與興趣，打破傳統課堂的學生被動的接受式學習的弊端，讓學生在具體而生動的對學習活動的參與實踐的過程中，去形象地探索和感知具體的幾何概型的求解方式，游戲教學法將抽象、深奧、難以理解的數學知識具體化、淺顯化，并進一步使學生感知到幾何概型是一種區別于古典概型的一種新的概率類型。讓學生在對游戲過程的理解和體驗的過程中，直觀形象地感知其中的內涵，不僅僅有很強的趣味性，同時也增強了學生對學習過程的高效參與，提高了學生在具體的學習實踐中對學習過程的有效理解和認識的程度，使得學習的效果得以更加有效地凸顯，同時，在具體的游戲實踐的參與過程中，有效地培養了學生用數學的眼光分析和看待生活中的數學問題的習慣，有效地促進了學生的數學抽象能力、邏輯推理能力、直觀想象能力等核心素養的培養。5.2 用實踐促進學生感知

在具體的學習實踐中，游戲與學生具體而生動的小組競賽游戲結合起來，讓學生在小組競爭機制的驅動下，積極地加入到對學習對象的探索、發現、歸納、總結等的過程中，從而使數學建模、數學推理、數學抽象等能力在具體的學生學習實踐中得到有效地構建。在具體而生動的學習參與實踐中，實現學生的核心素養的有效培養。

因此，在第三部分的小組合作學習實踐中，學習組內部是相互合作、相互促進的協同一致的關系，而小組和小組之間則形成了一種無形的競爭氛圍，小組與小組之間要展開實力與實力的較量，展開智力與智力的較量，因而，在趣味化的學習實踐的開展過程中，學生們在小組競爭的模式的支配下，必然會自覺地、主動地加入到小組內部的團結合作學習實踐中去，在具體的對學習對象的討論和參與的過程中，在多元化的交流體驗過程中，實現對學習對象的科學而有效地把握，同時學生們的知識模型也在相互的交流實踐中得到有效地建構，有效地促進了學生的數據分析、數學推理等能力的發展。

實踐是檢驗真理的唯一標準，在具體的理論與實踐相結合的實踐中，學生的幾何概型理論能夠在與實踐具體結合的學習實踐中得到有效地建構，從而有效地促進學生的數學建模素養的有效發展。學生的學習過程與實踐運用的結合能夠有效地提高學生對知識和理論等的理解的程度和深度，從而有效地培養學生用數學的眼光分析和看待生活中的問題的習慣的有效培養，使數學思維在具體的實踐應用的過程中得到有效地構建。

（作者單位：蘭州新區高級中學）