基于中國剩余定理的素數搜索算法
◆劉彥鑫
?
基于中國剩余定理的素數搜索算法
◆劉彥鑫
(青島理工大學 山東266520)
公鑰密碼算法是素數的一個重要應用途徑,例如經典的RSA算法現已滲透到人們信息生活的各個方面,保護著用戶的信息安全。公鑰密碼算法的優點在于不需要像對稱加密算法一樣采用安全的信道傳輸密鑰,但是公鑰密碼的計算開銷以及前期的素數產生開銷都比較大。針對素數產生開銷大這一問題,本文借助于中國剩余定理對素數在多維空間中的分布規律進行了研究,并在此基礎之上設計了一種相對高效的素數搜索算法,能夠有效減少在一個區間內搜索素數時所需檢查整數的數量,在一定程度上減小了素數搜索的負擔,增加了素數搜索的效率。
中國剩余定理;素數;初等數論;RSA
1 RSA公鑰密碼算法簡介
當前針對B/S模式下需要提供保密業務的WEB應用程序大多選擇RSA算法作為其信息加密方式以保證用戶信息在傳遞過程中的安全。RSA算法之所以能夠提供足夠的保密性是因為通常情況下RSA使用的素數非常大,選取大素數將為密碼破解者的破解過程帶來非常巨大的計算量,保證了密碼破解在所期望時間內是無法做到的,這稱之為計算上安全。為了更加深入的理解大素數在RSA算法中的作用,以及高效素數搜索算法對于RSA密鑰產生的重要意義,首先介紹RSA算法的密鑰產生過程:
( 1 ) 選取兩個保密的大素數p和q;
( 2 ) 計算n = p×q以及n的歐拉函數值φ(n) = (p-1)×(q-1);
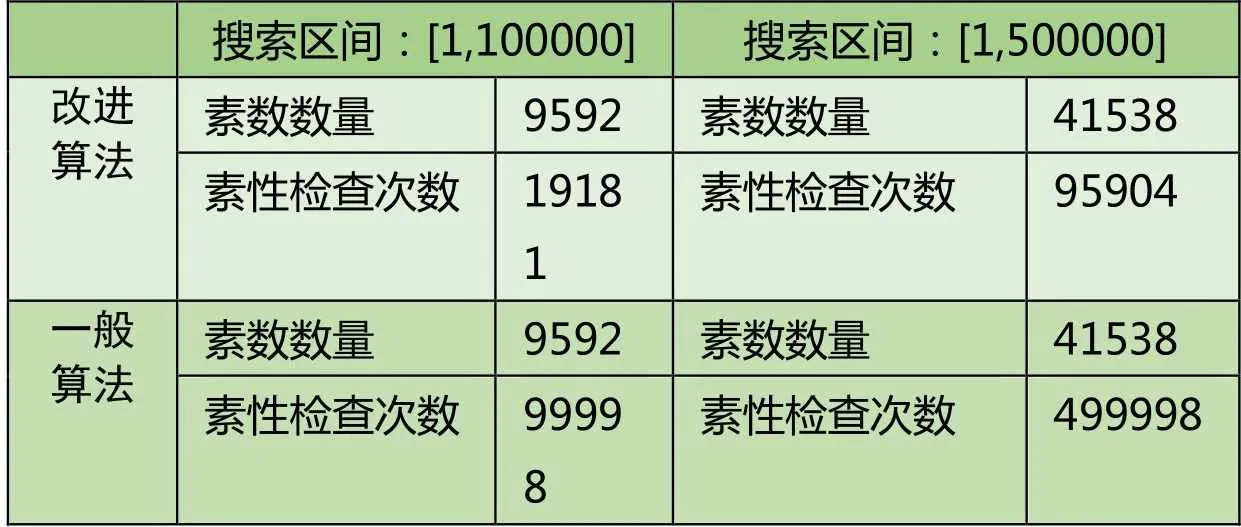
( 3 ) 隨機選擇一個整數e,使之滿足1 ( 4 ) 根據選擇的e計算與e配對的d,使d滿足d?e ≡ 1 mod φ(n)。 任何得到公鑰{e,n}的用戶均可對數據進行加密發送給私鑰的所有者,但加密的數據卻只能通過與公鑰配對的私鑰才能解密,這就保證了加密數據除私鑰的所有者外沒有人能夠解讀。 RSA算法的安全性依據是基于對大數n分解的困難性,要想通過公鑰中參數e得到私鑰中參數d就必須知道φ(n),也就是必須知道素數p和q,從而就必須對n進行分解,而n越大,將n分解還原出兩個素數就越困難。這就使得如果想要算法保證足夠的安全性就一定要選取足夠大的素數作為其計算參數。 但是大素數的生成目前是一件相當消耗資源的任務,原因在于檢測一個非常大的數是不是素數本身就比較費時,而現有素數搜索算法的時間復雜度往往是O(n)級別,這無疑更是加重了素數搜索任務的開銷。而如果能找到素數分布的大致規律,縮小素數搜索的范圍,便可在一定程度上降低素數搜索的開銷。 作為本算法的重要理論支撐,現簡要介紹中國剩余定理的基本內容。中國剩余定理又稱為“孫子定理”,是一種求解一次同余方程組的方法,是數論中一個重要定理。 在模下有唯一解: 中國剩余定理不僅提供了一種求解一次同余方程組的方法,同時還提供了一種數值映射方法,可將一個大整數映射為一組小整數組成的有序序列,本文將應用其數值映射方法探索素數的分布規律,并在算法實現中應用其求解同余方程組的方法確定一次搜索的起點。 圖1 [0,34]區間整數映射結果 圖2 [0,699]區間整數映射結果 圖3 算法性能優化程度散點圖 表1 算法性能檢驗實驗結果 從實驗結果不難看出,本文所述算法與一般算法相比,在保證不遺漏區間內任何素數素數的前提下所需檢查的整數數量更少。分析計算實驗數據可知:在區間[1,100000]內搜索素數時,算法性能優化程度為19181/100000 = 0.1918100。同樣,在區間[1,5000000]內搜索素數時,算法的性能優化程度為95904/500000 = 0.191808。可見,算法在實際應用中確實可以縮小搜索素數時整數的檢查范圍,且實際性能與理論分析結果出入不大。 本文針對素數的應用之一RSA算法做了簡要介紹,分析了RSA算法的安全依據以及開銷問題。而后對于本算法的理論基礎中國剩余定理做了簡要介紹,并利用中國剩余定理找到了素數分布的一個大致規律,發現了多維空間中部分素數不可能出現的位置,通過在素數搜索時避開對這些位置的檢查,從而達到了縮小素數搜索范圍的目的。而后給出了這一算法的實現思路,并對算法的性能進行了分析,給出了算法的性能優化公式以及性能的極限公式。文章最后利用Java語言對算法進行了實現,并利用真實的實驗數據檢驗了理論的正確性。 [1](加)Douglas R.Stinson.密碼學原理與實踐(第三版)[M].北京:電子工業出版社,2016:131-133. [2]郭亞軍,宋建華,李莉,董慧慧.信息安全原理與技術(第三版)[M].北京:清華大學出版社,2013:20-24. [3]王萍,廖芳燕,廖芳午,張樹貴.RSA算法中快速生成大素數方法的改進[J].重慶文理學院學報(自然科學版),2009,28(3):9-11.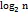
2 中國剩余定理
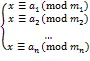

3 素數在多維空間中的分布規律


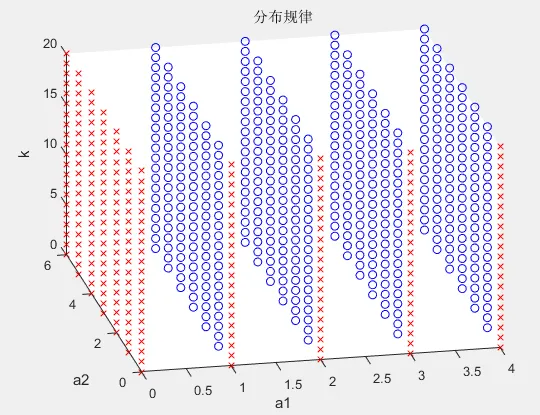
4 算法思路及性能分析

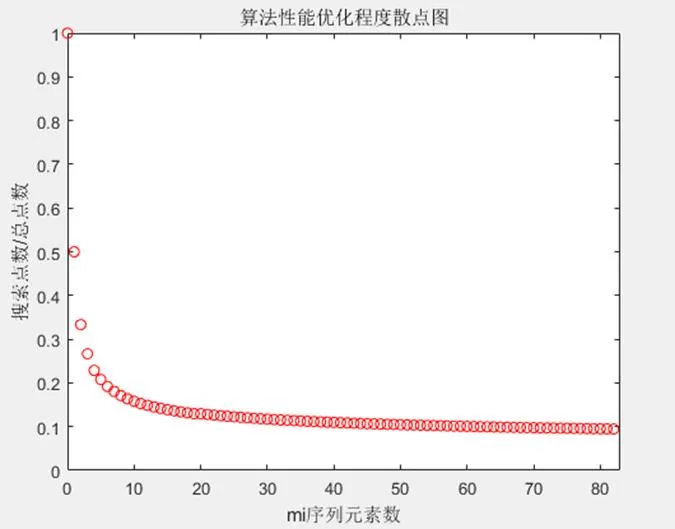
5 算法實驗結果及結論驗證
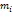
6 總結

