基于雙線性對(duì)的可驗(yàn)證可更新的向量空間秘密共享方案

◆張?jiān)葡?甘 勇 賀 蕾 莊 園 王冰麗

?

基于雙線性對(duì)的可驗(yàn)證可更新的向量空間秘密共享方案

◆張?jiān)葡?甘 勇 賀 蕾 莊 園 王冰麗

（鄭州輕工業(yè)大學(xué)計(jì)算機(jī)與通信工程學(xué)院 河南 450002）

目前，關(guān)于向量空間秘密共享方案都存在一定的局限性，其中大部分都是在信任中心參與下完成的。但是，信任中心的參與是不能夠確定的，所以，本文設(shè)計(jì)了一個(gè)新的方案，主要用于不存在信任中心的秘密方案中。在這種情況下，由參與者生成秘密，利用雙線性對(duì)的性質(zhì)，每個(gè)參與者都能夠測(cè)試秘密份額的有效性。在每個(gè)需要更新的地方，要求每個(gè)參與者選擇首個(gè)分量等于零的非零向量，以達(dá)到對(duì)秘密份額的定期更新。在方案的重構(gòu)階段，Hermirte插值定理用于重新構(gòu)造出秘密多項(xiàng)式，然后與雙線性對(duì)相結(jié)合以計(jì)算秘密。在方案結(jié)束時(shí)，分析了解決方案的正確性和安全性，并與現(xiàn)有解決方案進(jìn)行了比較，證明該方案具有較高的安全性、實(shí)用性和可行性。

信任中心；雙性線對(duì)；秘密重構(gòu)；Hermirte插值定理；秘密共享

0 引言

秘密共享是當(dāng)今生活中廣泛使用的技術(shù)，主要是對(duì)信息進(jìn)行加密、保護(hù)，防止外泄。1979年，Shamir和Blakley在文獻(xiàn)[1-2]中提出了一種門限秘密共享方案，在該方案?jìng)鬏敭?dāng)中，秘密被分成n份，再將n份秘密分給參與者，當(dāng)大于或等于t個(gè)參與者提供秘密份額時(shí)，才能重新構(gòu)造出秘密，其他情況一律不能夠重構(gòu)出秘密。在他們之后，研究秘密共享的學(xué)者就不斷增多，并在這個(gè)研究領(lǐng)域取得了一定的成果。

近年來(lái)，許多研究學(xué)者已經(jīng)開(kāi)始研究秘密共享技術(shù)，并提出了各種秘密共享方案，其中有中國(guó)剩余定理、雙線性對(duì)技術(shù)、簽密與消息恢復(fù)算法、公鑰密碼體制等。蔣華等人基于公鑰密碼體制，對(duì)802.1x進(jìn)行改進(jìn)，提出了一種雙向認(rèn)證的方案。只要是在申請(qǐng)人，身份驗(yàn)證者和服務(wù)器之間的相互身份驗(yàn)證，敏感域就可以通過(guò)相互身份驗(yàn)證加密[3]。2014年張等人提出了一種方案，在該方案中，秘密分發(fā)的過(guò)程是獨(dú)立的，并且與參與者的私鑰計(jì)算分開(kāi)。私鑰是由參與者自己來(lái)選擇保存的，比較容易實(shí)現(xiàn)。在分發(fā)和重構(gòu)過(guò)程中，參與者可以驗(yàn)證秘密共享的真實(shí)性。能夠預(yù)防參與者和分發(fā)者的不誠(chéng)信問(wèn)題，且敵手不易攻破[4]。

2018年，谷婷提出了一種秘密共享方案。在這個(gè)方案當(dāng)中，秘密份額由參與者產(chǎn)生，利用簽密與消息恢復(fù)算法，參與的所有人都可以查驗(yàn)分發(fā)者的秘密份額[5]。在此之前，雙線性對(duì)的秘密方案并不多，文獻(xiàn)[6]提出了一種雙向性對(duì)可驗(yàn)證的向量空間秘密共享方案，該方案能夠提高對(duì)秘密份額驗(yàn)證的有效性，充分展現(xiàn)了雙線性對(duì)的優(yōu)勢(shì)，但此方案不能夠?qū)崿F(xiàn)動(dòng)態(tài)性，也不可能定期更新秘密。文獻(xiàn)[7]中，秘密共享的參與者就是分發(fā)者，不需要其他人來(lái)分發(fā)秘密，但此方案不能驗(yàn)證秘密份額的合法性和正確性，同時(shí)也不能對(duì)秘密份額進(jìn)行定期的更新。

在秘密方案中，所有的秘密都基于有限域[8]或加法群[9]上的, 2014年，尚等人提出了一個(gè)新的方案，在他的方案中，參與秘密分享的人必須要有兩個(gè)秘密份額，否則就不能夠重新構(gòu)造秘密，并且在秘密分發(fā)的同時(shí)生成驗(yàn)證信息。每個(gè)人都能夠驗(yàn)證秘密份額，在秘密份額被竊取時(shí)都能夠及時(shí)檢測(cè)，防止竊取和欺騙行為。在重構(gòu)階段，一種新的定理被用來(lái)重建秘密多項(xiàng)式，這就是Hermite插值定理和雙線性運(yùn)算結(jié)合的結(jié)果[10]。本文在文獻(xiàn)[10]的基礎(chǔ)上，選取每一更新點(diǎn)的第一分量為零的非零向量，實(shí)現(xiàn)秘密份額的更新，并針對(duì)Diffie-Hellman問(wèn)題，在安全性分析計(jì)算性問(wèn)題方面做了進(jìn)一步的認(rèn)證。

1 準(zhǔn)備知識(shí)

1.1 雙線性對(duì)

定義1在為素?cái)?shù)的前提下，設(shè)定階為的加法組為1，階為的乘法組2，如果存在，且映射:1×1→2存在，滿足以下屬性，映射稱為雙線性映射:

（1）雙線性性：對(duì)任意,∈1，有(,) =(,)。

（2）非退化性：存在,∈1，使得(,)≠1。

（3）可計(jì)算性：對(duì)任意,∈1，存在有效算法計(jì)算(,)。

1.2 Hermite插值

已知函數(shù)()在個(gè)互異點(diǎn)1,2, …,n處的函數(shù)值(1) ,(2) , …,(x) 及一階導(dǎo)數(shù)'(1) ,'(2) , …,'(n) ,2n-1()這個(gè)多項(xiàng)式滿足下面的條件：

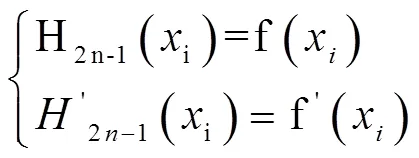
其中,=1, 2, …,。

Hermite插值多項(xiàng)式2n-1()的其一般表達(dá)式為:

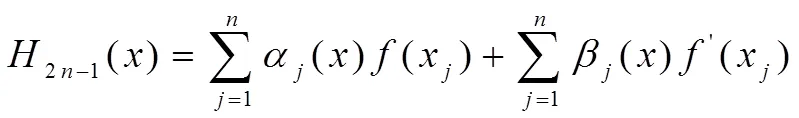
其中α()和β()稱為Hermite插值基函數(shù)

1.3 相關(guān)問(wèn)題

設(shè)定階為的加法組為1，乘法組2，它們之間有映射，會(huì)出現(xiàn)以下數(shù)學(xué)難題：

（1）計(jì)算性Diffie-Hellman (CDH)問(wèn)題：對(duì)于為1的生成元，在已知,,的情況下，計(jì)算是困難的。

（2）雙線性Diffie-Hellman(BDH)問(wèn)題：給定 (,,,) , 計(jì)算(,)∈2。設(shè)算法A用來(lái)解決BDH問(wèn)題, 其優(yōu)勢(shì)定義為, 如果:

目前，還未有有效的算法解決此問(wèn)題。因此我們可以假設(shè)BDH問(wèn)題是一般困難的

2 方案構(gòu)成

2.1 系統(tǒng)初始化

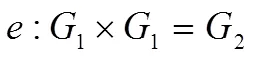
2.2 份額分發(fā)

秘密分發(fā)過(guò)程為:

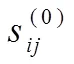
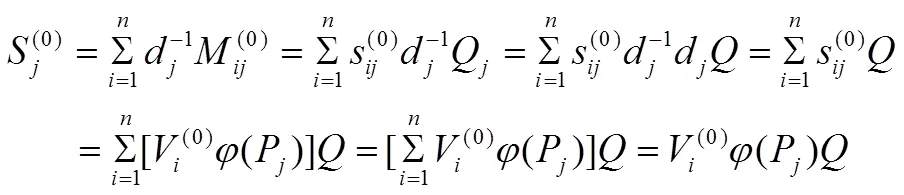
其中,=1, 2, …,。

2.3 份額更新

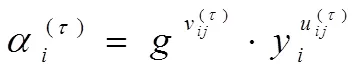
2.2 秘密恢復(fù)

秘密恢復(fù)過(guò)程如下：

（1）參與者P利用自己的私鑰x計(jì)算：

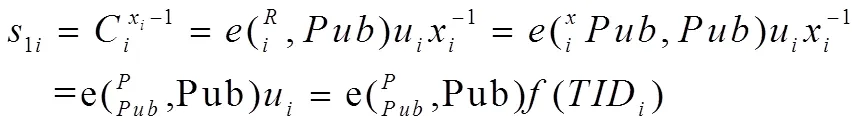
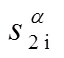
（2）設(shè)有個(gè)參與者1,2, …,P合作重構(gòu)秘密,，檢驗(yàn)者檢驗(yàn)下式的正確性，以此來(lái)確定秘密份額是否有效。

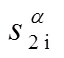
如果有個(gè)以上都能夠檢驗(yàn)正確，運(yùn)用2個(gè)1j(=1, 2, …,) 和2j(=1, 2, …,) , 結(jié)合雙線性對(duì)和Hermite定理就能夠得到以下結(jié)論:

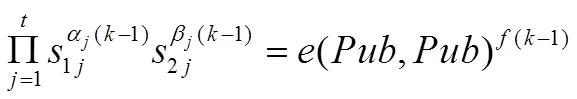
其中：

由于k=(-1) , 因此可以得出:

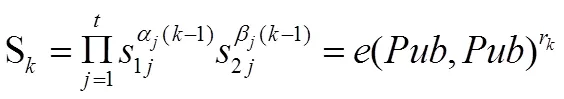
3 方案分析

3.1 正確性分析

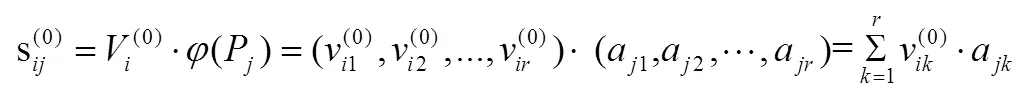
由此可見(jiàn)，定理1成立。

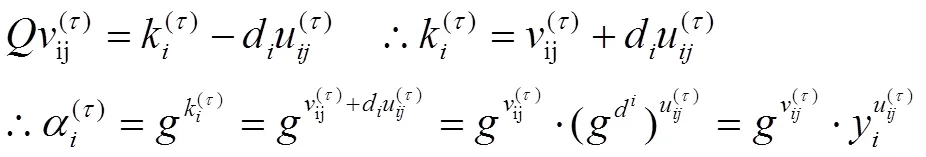
由此可見(jiàn)，定理2成立。

定理3 在驗(yàn)證參與者提供秘密份額的真實(shí)性階段式(3)是正確的。

由此可見(jiàn)，定理3成立。

定理4 在份額重構(gòu)階段式(4)是正確的。

又因?yàn)?i>r=(-1)，所以：

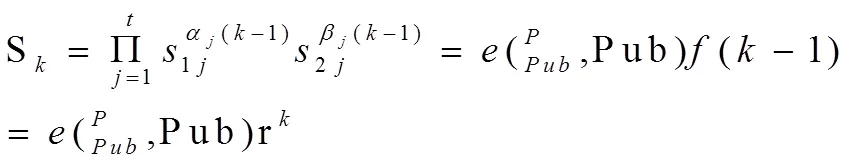
由此可見(jiàn)，定理4成立。

3.2 安全性分析

定理1在BDH的前提下, 除參與者以外的都可以使用公共的信息來(lái)得到1i,2i(=1,2,…,) 是不可能的。

證明：用反證法。讓BDH假設(shè)正確, 但敵手沒(méi)有私鑰x，使用公開(kāi)信息,R,,,計(jì)算出秘密份額1i,2i(=1,2,…,)。

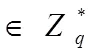
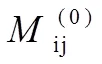
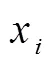
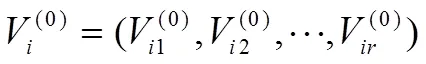
本方案在保證安全性的前提下，能夠增加方案的性能，尤其是在多個(gè)秘密、無(wú)可信中心、公開(kāi)驗(yàn)證和秘密更新中，不需要維護(hù)安全信道，并且參與者可以發(fā)送要在公共信道上傳送的信息，從而避免了秘密在分發(fā)階段的頻繁操作。任何人都能夠公開(kāi)核實(shí)秘密份額。在份額更新中能定期更新秘密份額。以上的安全性分析方法也進(jìn)一步的證實(shí)了該方案的正確性，具有一定的實(shí)用價(jià)值。

將本方案與方案[4]、方案[6]、方案[7]和方案[10]進(jìn)行了對(duì)比，如表1所示。從表1中我們可以得出結(jié)論，該解決方案不需要信任中心參與，并且可以公開(kāi)驗(yàn)證秘密份額，還能更新秘密份額。

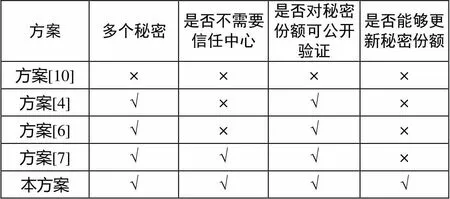
表1 性能比較

4 結(jié)束語(yǔ)

本章基于雙線性對(duì)的特定屬性，構(gòu)建了一個(gè)可驗(yàn)證、可更新的向量空間動(dòng)態(tài)秘密共享方案。該解決方案不需要受信中心的參與，也不需要安全信道，并且秘密份額由參與者生成，利用雙線性對(duì)的性質(zhì)，每個(gè)人都可以驗(yàn)證分發(fā)的秘密份額的正確性。與其他類似方案相比，改進(jìn)了向量空間中秘密共享方案的實(shí)用性，證明了該方案在性能上具有一定的優(yōu)勢(shì)，但本方案的計(jì)算復(fù)雜度相對(duì)其他方案較高，在今后的工作中會(huì)繼續(xù)研究改進(jìn)。

[1]Blakley GＲ．Safeguarding Cryptographic Keys［C］/ /Proceedings of AFIPS National Computer Conference．Washington D.C,USA: IEEE Press，1979: 313-317．

[2]Shamir A.How to Share a Secret［J］.Communications of the ACM ，1979，22( 11) : 612-613

[3]蔣華,張樂(lè)乾,阮玲玲.基于公鑰密碼體制的802.1x雙向認(rèn)證研究[J].計(jì)算機(jī)應(yīng)用與軟件,2016,33(02):290-293.

[4]張柄虹,張串絨,焦和平,張欣威,高勝國(guó).一種基于雙線性對(duì)的公開(kāi)可驗(yàn)證多秘密共享方案[J].空軍工程大學(xué)學(xué)報(bào)(自然科學(xué)版),2014,15(04):83-87.

[5]谷婷.無(wú)可信中心可驗(yàn)證可更新的向量空間秘密共享[J].科技與創(chuàng)新,2018(03):29-33.

[6]Zhang Jie, Zhang Futai.Information-theoretical Secre Verifiable Secret Sharing with Vector Space Access Strures over Bilinear Groups and Its Applications[J].Future Generation Computer Systems, 2015, 52 (5) :109-115.

[7]張倩倩,李志慧,雷娟.基于向量空間上的無(wú)分發(fā)者的秘密共享方案[J].計(jì)算機(jī)應(yīng)用研究,2011,28(06):2230-2232.

[8]Kaya K, Selcuk A.A Verifiable Secret Sharing Scheme Based on the Chinese Remainder Theorem[C]//Proceedings of INDOCRYPT’08.Berlin, Germany:Springer-Verlag, 2008:414-425.

[9]田友亮, 馬建峰, 彭長(zhǎng)根, 等.橢圓曲線上的信息論安全的可驗(yàn)證秘密共享方案[J].通信學(xué)報(bào), 2011, 32 (12) :96-102.

[10]尚雪嬌,杜偉章.基于雙線性對(duì)的可公開(kāi)驗(yàn)證多秘密共享方案[J].計(jì)算機(jī)工程,2014,40(09):155-158+166.

國(guó)家自然科學(xué)基金61572445，國(guó)家自然科學(xué)基金61772477，國(guó)家自然科學(xué)基金聯(lián)合重點(diǎn)項(xiàng)目U1804263，河南省科技計(jì)劃項(xiàng)目資助項(xiàng)目 172102210064。