大規模云計算服務器優化調度問題的最優二元交換算法研究

王萬良，臧澤林，陳國棋，屠杭垚，王宇樂，陸琳彥

（1. 浙江工業大學計算機科學與技術學院，浙江 杭州 310027；2. 倫敦大學國王學院工程科學學院，英國 倫敦 WC2R 2LS）

1 引言

云計算是分布式計算（distributed computing）、網絡存儲（network storage technology）、負載均衡（load balance）等傳統計算機和通信技術發展融合的產物，由于云計算技術的通用性和高可靠性，該技術得到了廣泛的發展[1]。隨著云計算規模的逐步擴大，谷歌、阿里巴巴、百度等大型互聯網企業紛紛搭建了自己的云服務平臺。它們建立的平臺可容納超過萬臺的服務器，為超過百萬的用戶進行服務。大規模云服務平臺的建立，使云服務的調度系統變得更加重要[2]。在龐大的云服務平臺基數下，云服務平臺的性能即使有1%的提高也會帶來巨大的收益[3]。

目前，云計算調度分為云服務請求實時調度和基于歷史數據的云服務優化調度。

云服務請求實時調度以調度系統的快速性、穩定性為出發點，研究如何實時地將云計算任務指派給一臺或幾臺宿主機服務器實現負載均衡。在這類研究中，傳統的方法有Max-Min方法[4]、RR算法[5]、FCFS算法、FIFO算法[6]等。另外，一系列的商業軟件如 Google的 Borg調度系統[7-8]、阿里巴巴的Sigma調度系統[9]和MapReduce等開源軟件都做出了相應的學術貢獻。但是上述研究存在以下2個尚待解決的問題：1)上述方法只能應用于過程迭代和異構任務類型，無法執行遞歸或復雜的業務流；2)上述方法會出現占用特定的虛擬機 I/O，造成其他作業“饑餓”的情況。

在基于歷史數據的云服務優化調度領域，同樣出現了大量的研究成果。其中，Tsai等[10]闡述了實時的云計算的生命周期問題，并在此基礎上提出了一種面向云計算實時調度的框架，該框架能夠有效地解決云計算實時調度的一般問題。在此基礎上，Zhu等[11]提出了一種用于虛擬化云中實時任務調度的新型滾動調度架構，然后提出并分析了面向任務的能耗模型。另外，Zhu等[11]開發了一種新的能量感知調度算法（EARH, energy awar），并通過實驗證明了該算法能夠在可調度性和節能之間做出良好的權衡。王吉等[12]在考慮調度快速性和有效性的背景下，又考慮了調度的容錯性，提出了一種在虛擬云平臺中的容錯調度算法（FSVC, fault-tolerant scheduling algorithm in virtualized cloud），通過主副版本方法實現對物理主機的容錯控制，采用副版本重疊技術與虛擬機遷移技術提高算法的調度性能。郭平等[13]將云平臺的調度問題簡化為本地化的調度問題，并且結合主導資源公平調度策略 DRF和Delay調度約束機制，提出了一種滿足本地化計算的集群資源調度策略（DDRF, delay-dominant resource fairness），并討論了本地化計算時延對作業執行效率的影響。另外，對于提供 GPU服務的云平臺，Peng等[14]提出了一種高效的、動態的深度學習資源調度方法—— Optimus，該方法使用在線訓練來擬合訓練模型，并建立性能模型以準確地估計每個作業的訓練速度。就工作完成時間而言，Optimus的調度性能有63%的提高。

基于歷史數據的云服務優化調度將同一云計算請求源產生的計算請求看成是可預測的時間序列。調度算法以該時間序列為基礎對宿主機服務器的分配進行調度[15]。很多經典的優化方法和優化理論可以引入調度框架[16]中，如遺傳算法（GA, genetic algorithm）[17]、群智能算法、局部搜索（LS, local search）算法[18]等。同時，有部分學者提出了專門面向服務器的調度算法。例如，林偉偉等[19]通過對約束滿足問題對異構的云數據中心的能耗優化資源調度問題建模，并且在此基礎上提出了能耗優化的資源分配算法（DY, dynamic power）。Li等[20]提出了一種協調調度算法來解決過度生成虛擬機（VM, virtual machine）實例的問題，并使用實際生產中的數據驗證了該方法的有效性。Dong等[21]將云服務器調度問題建模為混合整數規劃（MIP, mixed integer programming）問題，將目標函數設置為使數據中心服務器消耗的能量最小，并提出了一個有效的服務器優先任務調度方案。

為了克服分支定界算法解決大規模問題時間消耗龐大的問題，本文將LS算法[22]的框架融入分枝定界算法，設計了最優二元交換算法（OTECA,optimal two element exchange algorithm）。OTECA并不是使用分支定界法一次性解決全部問題，而是每次只解決其中的部分子問題。然后使用LS的思想不斷地選擇子問題進行解決。因此，OTECA可以通過求解多個子問題獲得原問題的解。上述求解策略可以快速有效地求解大規模的服務器調度問題。實驗證明，OTECA優于LS、GA等算法。

2 云計算服務器調度模型

本節建立一個MIP模型，對云計算服務器調度問題進行描述。模型框架如圖1所示。

圖1顯示了云計算調度資源、調度方案、目標函數、約束條件與運算請求間的相互關系。本節將用數學方式對上述單元以建模的方式進行描述。

2.1 云計算服務器的資源表示與數據描述

在整個調度過程中，需要處理的資源被抽象為5個集合：服務器集合M、應用集合A、實例集合S、親和約束集合Q與反親和約束集合F。

每個宿主機服務器mj都可以提供多種類型的計算資源，服務器集合M可描述為

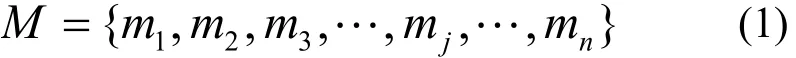
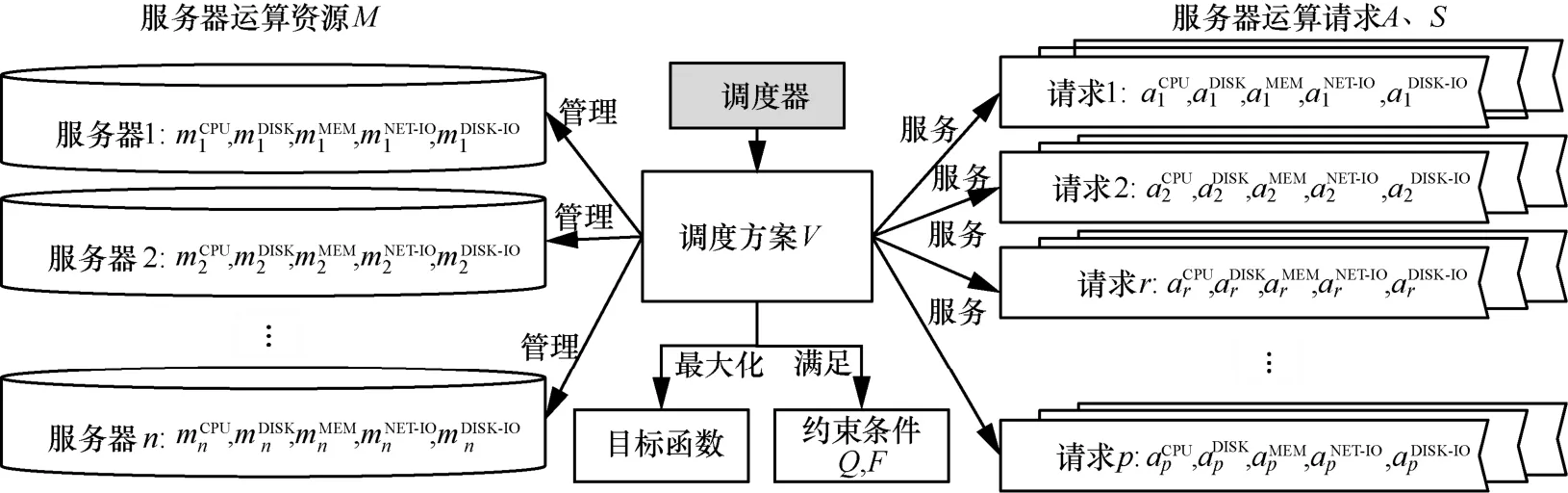
圖1 云計算服務調度模型框架

其中，n為服務器的數量，mj為第j臺服務器所能提供的資源，即

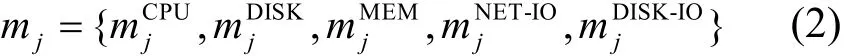
應用集合A描述了請求服務器資源的應用與其對服務器提供資源的消耗，即

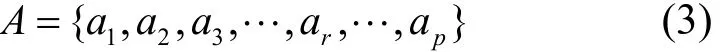
其中，p為應用的總量，ar為第r個應用需求的資源，即

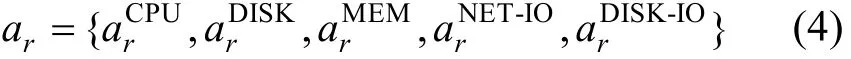
其中，CPU、DISK與MEM的每日資源消耗按照時間曲線給出，NET-IO、DISK-IO的每日資源消耗以常數的形式給出。為元素個數為N的列向量，其中k為時間維度的檢索句柄，滿足k∈{1,2,3,…,N}。

相互獨立的運算請求被稱為實例。實例集合S包含調度過程中應用產生的所有實例，即

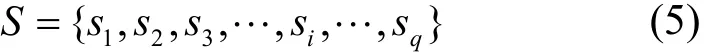
其中，q為實例的總量，實例si為

親和約束與反親和約束描述了調度場景中的約束關系，主要分為2種情況：應用與應用之間的親和/反親和關系，應用與服務器之間的親和/反親和關系。

親和/反親和關系可以描述為2個應用之間（或者應用與宿主機服務器之間）存在相互依賴或者相互排斥的關系。具體的親和/反親和關系描述如表 1所示。

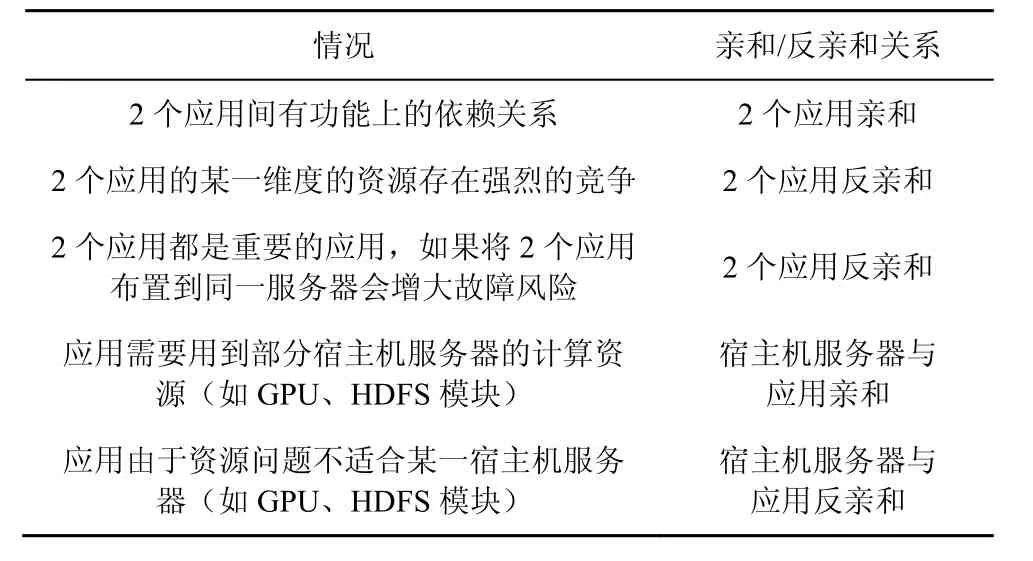
表1 親和/反親和關系描述

親和/反親和的關系使用 0-1矩陣Haa、Ham、Faa、與Fam描述。應用與應用間的親和關系Haa的結構描述為

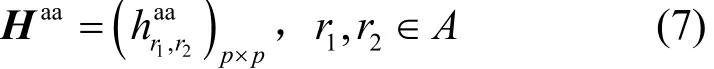
Faa的結構與Haa的結構相同，其矩陣內元素為，當時，r1應用與r2應用不存在反親和關系，反之存在。Ham的結構描述為

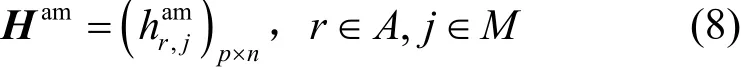
其中，Ham描述應用與機器間的親和關系。

Fam的結構與Ham的結構相同，其矩陣內元素為當時，r應用與j機器不存在反親和關系，反之存在。

2.2 云計算服務器調度的決策變量與目標函數

云計算服務器的調度問題乃至大部分的資源調度問題都可以轉化為一個多維度的背包問題。調度的目的是為每一個計算請求（實例si）尋找一個合適的宿主機服務器mj，減少系統的運行成本。因此以0-1整數的形式，定義二維決策變量V描述實例到機器的分配關系，即

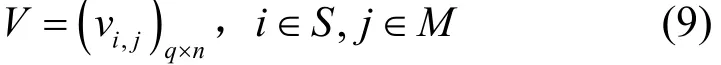
其中，vi,j為0-1決策變量，vi,j=1代表實例s1被調度到機器mj中執行，反之沒有。

為了方便對親和/反親和約束描述，另外，設定輔助決策變量W來描述應用到機器的分配關系，即

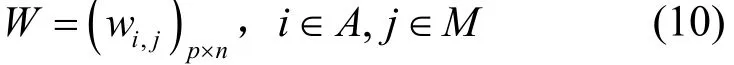
其中，wi,j為0-1決策變量，wi,j=1代表應用ai被調度在機器mj中執行，反之沒有。V與W之間存在的約束關系為

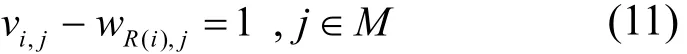
其中，R(i)為一個從實例Si到其對應的應用的映射。優化調度的目標描述為：在一定調度時間段內，尋找一種使用服務器數量最少、負載均衡的服務器調度方案。為了避免由于模型不精確帶來的資源使用溢出風險，本文通過懲罰的形式定義目標函數為

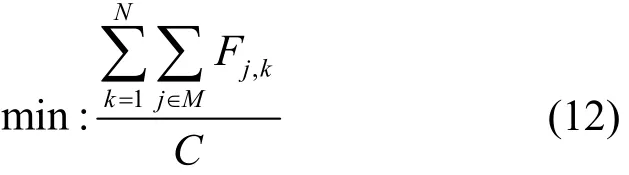
其中，k為時間索引，滿足k∈{1,2,3,…,N}；C為時間采樣頻率；Fj為宿主機服務器mj獲得的分數值，其可以描述為

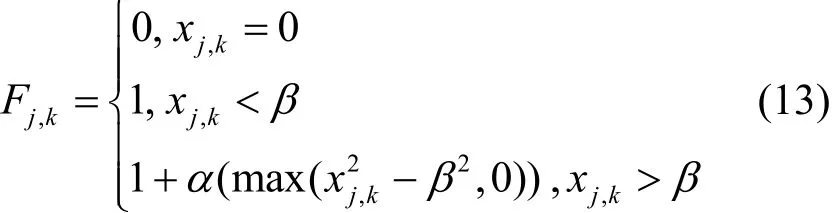
其中，β為懲罰閾值，當宿主機服務器的CPU使用率大于懲罰閾值時，開始引入額外平方項對調度方案進行懲罰；α為懲罰增量系數，描述進行懲罰時的懲罰力度；xj,k為機器mj在k時刻的CPU使用率，計算式為

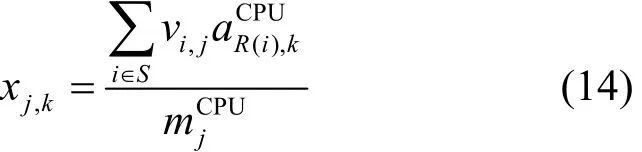
單一機器 CPU使用率與目標分數關系如圖 2所示。由圖2可知，當機器在所有的時間內保持CPU使用率為0時，目標分數為0；當機器的CPU使用率大于0且小于懲罰閾值β時，目標分數為1；但當CPU使用率大于懲罰閾值時，目標分數從1開始以二次冪形式上升。

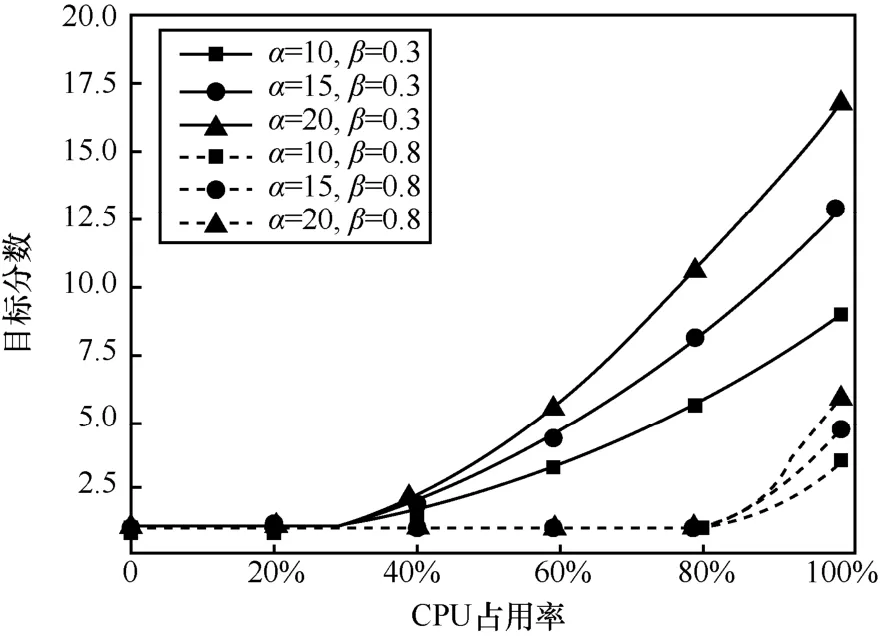
圖2 單一機器CPU使用率與目標分數關系

2.3 云計算服務器調度的約束條件

實際的云計算服務器調度環境中存在大量由硬件條件和應用功能導致的限制。模型將這些限制轉化為模型約束、資源約束、親和/反親和約束和優先級約束進行處理。

模型約束描述了調度模型的基本約束，包括每個實例都應被安排到一個宿主機服務器上，且只能被安排到一臺宿主機服務器上，即

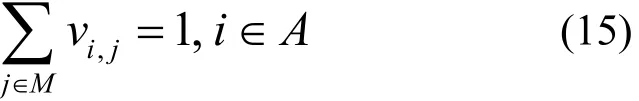
資源約束是一種由于資源限制造成的約束，每個宿主機服務器上配置的不同類型的資源是有容量上限的。

CPU資源約束為

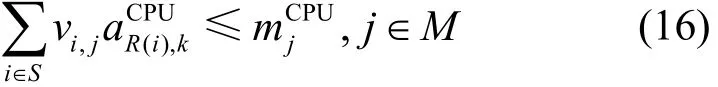
DISK資源約束為

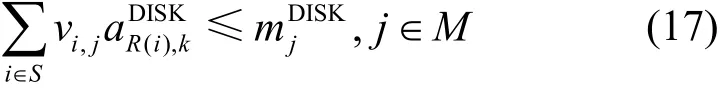
MEM資源約束為

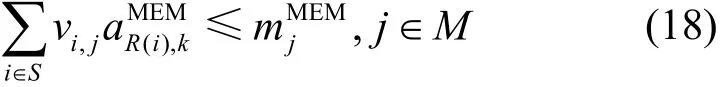
NET-IO資源約束為

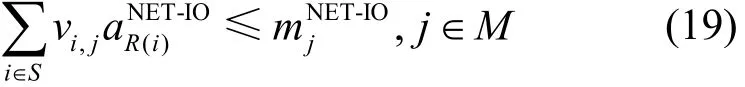
DISK-IO資源約束為

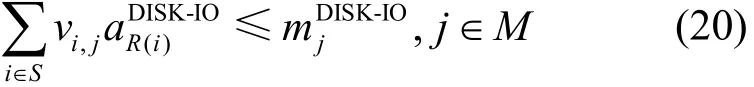
親和/反親和約束可以分為以下4種情況。

1) 應用與應用的親和約束

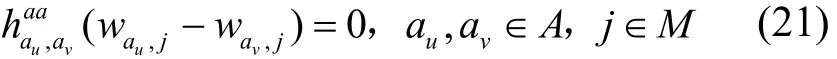
2) 應用與應用的反親和約束

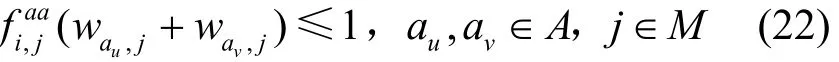
3) 應用與機器的親和約束

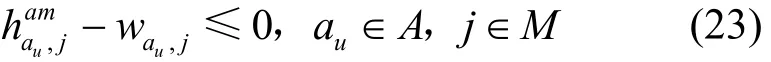
4) 應用與機器的反親和約束

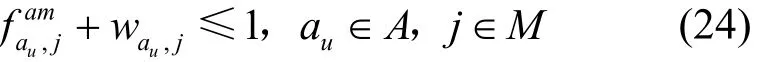
約束決策變量不能同時為1。

3 大規模云計算二元交換分析論證

將式(13)寫成max函數形式，定義評分函數為

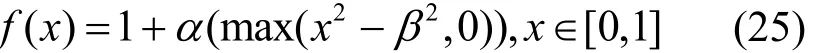
其中，x為宿主機服務器某一時刻的CPU使用率，機器j的CPU使用率為xj。

引理1在所有對2臺機器進行的CPU使用率(x1,x2)的重新分配(x1*,x2*)中，至少存在一個使評價分最小的最優分配，且該最優分配可由計算式和求得，其中，c為2臺機器的CPU容量的比例，即

證明將式(14)代入Ot(x1,x2)=f(x1)+f(x2)可得

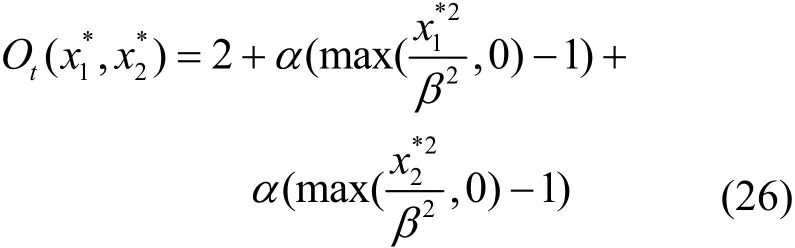
由于實例的重新分配不改變其 CPU使用率絕對值之和，因此有

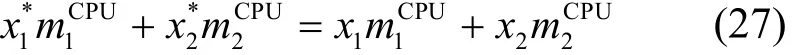
因此，可以表示成l(·)，即，將其代入式(26)，可得變量為x1*的方程為

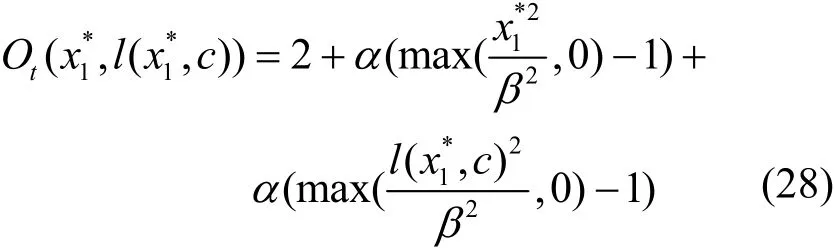
對式(28)進行分段討論后再對x1*求導可得

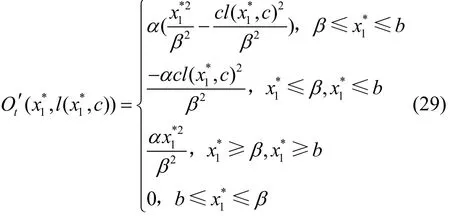
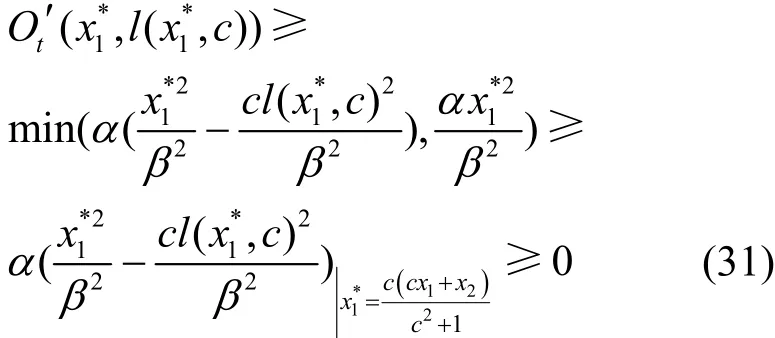
引理2定義機器j的特征計算式為xj為機器j的平均CPU使用率。在2臺機器的平均CPU占比為(x1,x2)的情況下，最優分配(x1*,x2*)所帶來的評分之和的下降量Od(x1,x2,c)=Ot(x1,x2)-Ot(x1*,x2*,c)與 2臺機器的特征計算式的差的平方(g1-g2)2呈正相關。

證明對特征公式的差的平方(g1-g2)2進行展開，有

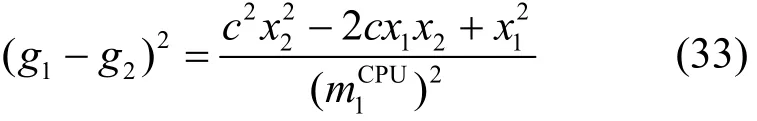
構造函數

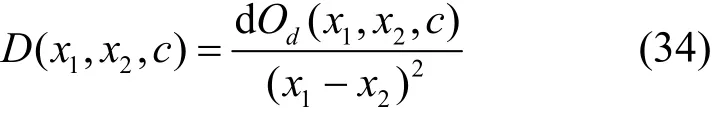
對于所有的自由變量，使用鏈式法則進行展開，可得

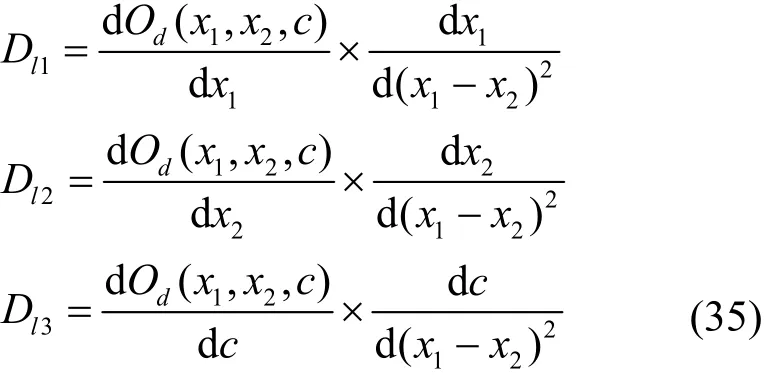
其中

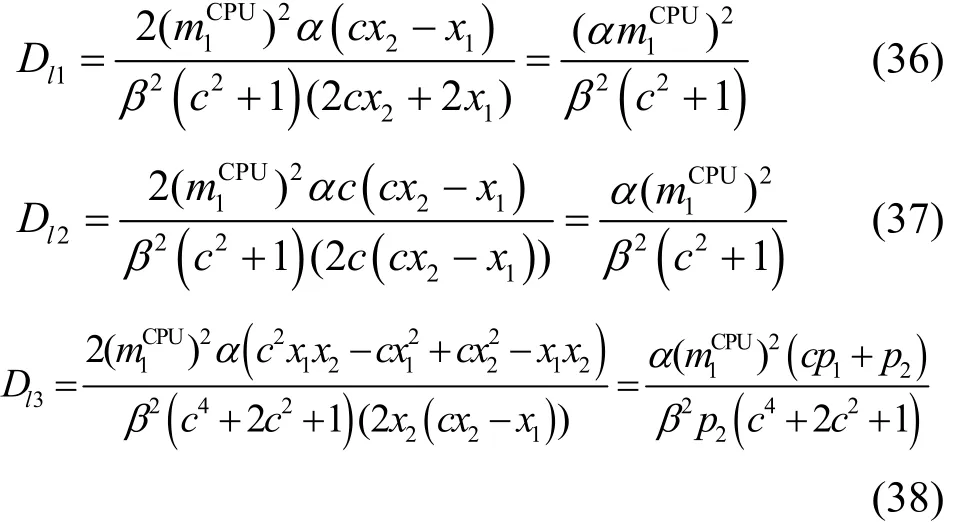
由于α、β與c皆大于或等于 0，Od對于特征計算式p的導數恒大于0，即D(x1,x2,c)＞0，因此2個方程呈正相關。證畢。

4 算法設計

混合整數規劃問題是一個NP完全問題，即求解該問題的最優解的時間復雜度與問題的規模呈指數關系。隨著數據量的增長，分支定界法不能在有效時間內得到理想的解，基于此，本文設計了OTECA，尋找一個時間花費與求解精度的平衡點，快速有效地解決云計算服務器調度問題。

4.1 可行解生成方法

可行解生成方法負責生成占用盡量少的服務器資源且滿足約束要求的初始解。求解的流程如算法1所示。

算法1可行解生成方法（GSSM, good solution generation method）

輸入服務器集合M，應用集合A，實例集合S

輸出調度初始可行解V，狀態矩陣E

1) 初始化可行解V，使用服務器數下限Nml=0，使用服務器數上限Nmh=p

2) whileNml!=Nmhdo

3) 機器指示m=0

4) for 實例索引s=0,s≤q,s++

5) if 實例s可裝入機器mthen

6)V,E=put(s,m) %將s放入m中，并更新狀態

7) else

8)m=m+1,s=s-1

9) end if

10) ifm==Nmhthen %機器數選取過少

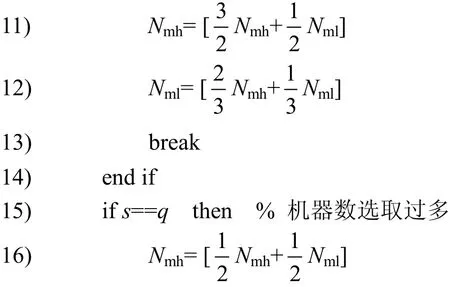
17) end if

18) end for

19) end while

20) returnV,E

算法通過二分法的形式對使用服務器數量的上限和下限不斷更新，從而不斷地拉近使用服務器的上下限的差距，最終在上下限相等時停止程序，完成對最合適的可行解的生成。步驟5)驗證機器m裝入實例s后，是否仍然滿足模型約束。步驟 10)與步驟 15)判斷當前的機器數量上限Nmh能否得到可行解，如果可以得到可行解，則進一步減少機器數量，如果無法得到可行解，則增加機器的數量，直至上下限相等則退出方法。

在時間復雜度方面，由于每次進入步驟 11)、步驟12)與步驟16)判斷都會造成Nmh與Nml的差減少一半，因此外部循環的復雜度為log(p)。步驟4)～步驟18)的內部循環的次數受到實例數p與機器數n的影響，在最壞的情況下將進行n+p次循環，因此整個算法的時間復雜度為(n+p)log(p)。

4.2 最優二元交換算法

分支定界法求解大規模MIP問題消耗的時間常常是不能接受的，但是求解較小規模的MIP問題卻有很高的效率。該算法將通過求解一系列小規模的 MIP子問題，去逼近整個大規模的 MIP問題。

可以證明，在所有的實例都滿足約束被分配進入宿主機服務器的情況下，將其中2臺機器中的實例以 BBM 方法重新分配到原來的宿主機服務器中，不會造成調度目標值的上升（如引理1所示），且這2臺機器的特征計算式gj差距越大，其獲得更高分數下降的可能性也就越大（如引理2所示）。

OTECA流程如圖3所示。

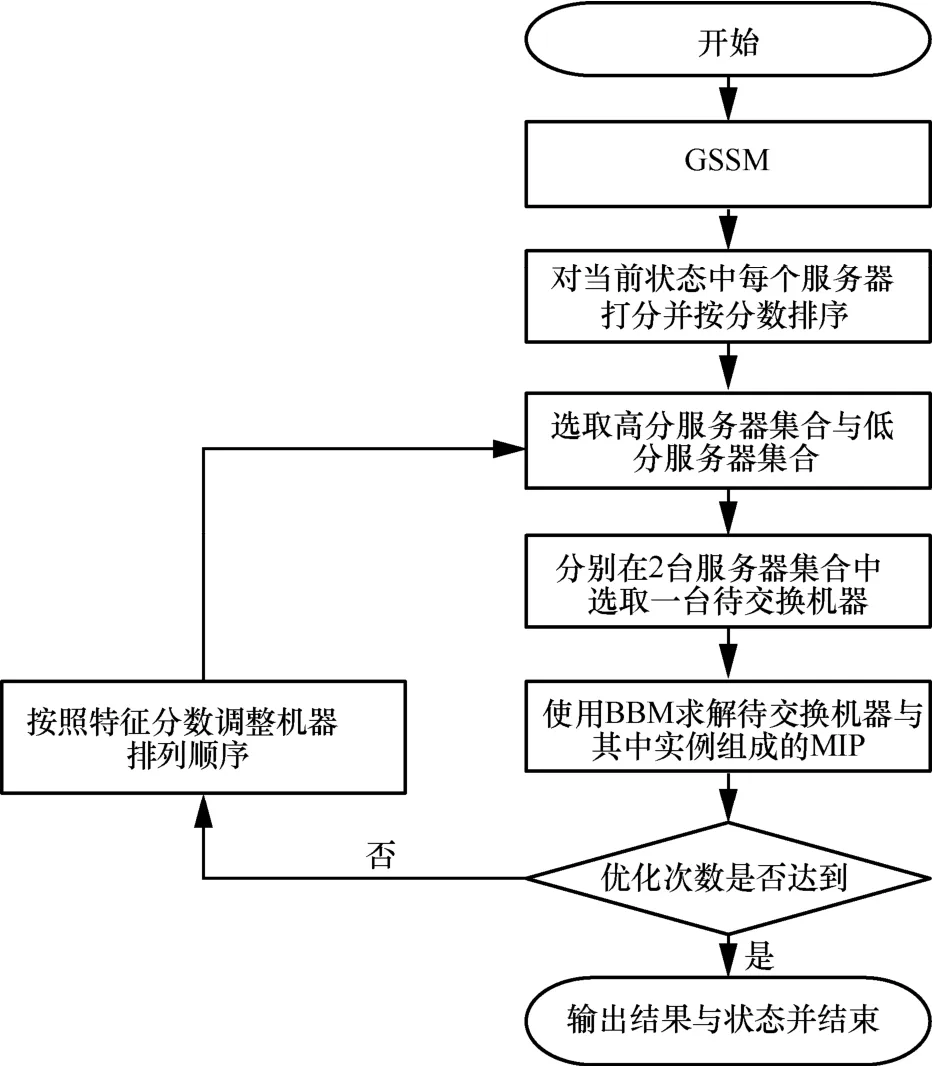
圖3 OTECA流程

最優二元交換算法偽代碼如算法2所示。

算法2OTECA

輸入服務器集合M，應用集合A，實例集合S，懲罰系數α和β，集合選擇系數γ，小規模MIP子問題求解次數Ns

輸出服務器調度結果Vbest

1)V=GSSM(M,A,S) %生成可行解

2)M,ScoreList=Score(E,M) %按照式(14)對當前可行狀態中每個服務器進行打分，并按照分數進行排序

3) for loop=0, loop＜Naim, loop++

4)M=SMWS(M, ScoreList) %按照分數調整順序

5)Smh,Sml=CMSet(Mc,A,S,α,β,γ) %選取高分服務器集合與低分服務器集合

6)Mh,Ml=ChoMach(Smh,Sml) %分別在2臺服務器集合中選取一臺待交換機器

7)VMIP,E=BBM(Mh,Ml,A,α,β)%分支定界法求解該小規模MIP問題，得到新的分配方案與機器狀態

8) end for

9) returnVbest

最優二元優化部分是算法的核心部分，該部分為尋找一個優秀的大規模服務器調度方案，其主要循環中包括高分機器集合與低分機器集合的維護、MIP子問題選擇、MIP子問題求解等步驟。

步驟 4)和步驟 5)生成一個高分機器集合與低分機器集合，其中特征分數概念由目標函數中目標分數的概念變化而來。該特征分數綜合考慮了機器當前負載與機器的容量這2個特性，可以表現機器未來的負載能力，如引理 2所示。步驟 5)中，使用最高分sh與最低分sl生成高分集合與低分集合，生成的標準為

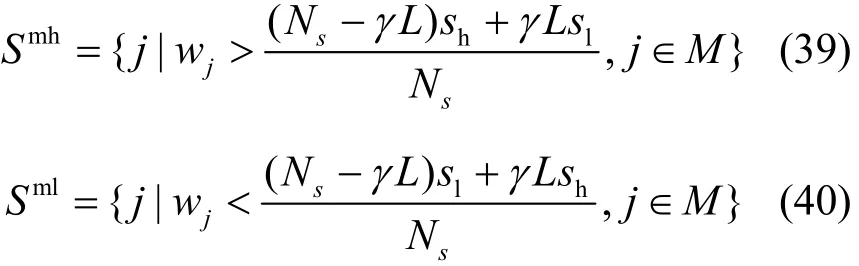
其中，γ為集合選擇系數，一個較大的值可以使高分機器集合和低分機器集合隨循環次數的選擇增長得更快；Smh為高分機器集合，Sml為低分機器集合。

步驟7)中設定當機器得分不變的前提下，實例負載盡量裝入容量較大的服務器，從而盡量減少服務器的使用。步驟 4)～步驟 7)不斷解決子問題優化調度結果。

每個循環子問題由高分機器、低分機器與機器中的實例組成。子問題的最優解一定是上述實例在上述機器上的重新組合。可以證明，新解的目標分數之和一定優于原解（如引理 1所示）。另外，高分機器與低分機器的分差越高，重新組合后分數的優化越顯著（如引理 2所示）。上述引理是算法挑選高分集合和低分集合進行混合的原因。因此，最優二元優化算法比傳統的基于隨機或啟發的算法有更強的目的性，在前期擁有更高的收斂速度，在后期擁有更強的調度精確度。

算法初始階段將快速地消除高負載機器，造成低負載機器分數上升、高負載機器分數下降，這時高分機器集合和低分機器集合將出現一定重疊。隨著這種重疊現象的逐步加深，算法的子問題選擇將逐漸退化為對機器的隨機優化，從而對機器中實例進行整理，并減小宿主機服務器的數量。最后該算法將返回從實例到宿主機服務器的優化分配。

在時間復雜度方面，4.1節已經論證了算法 2步驟1)的復雜度為(n+p) log(p)，步驟2)作為一個排序的工作，復雜度為nlog(n)。因為步驟3)～步驟7)在最壞情況下復雜度為Naim2x，其中x為子問題中實例的數量，這并不意味著該步驟是十分耗時的，因為在子問題中，x受到機器容量的約束。在實際的應用環境中，步驟7)均可以在可接受的時間（秒級）范圍內得到響應，則算法2總的時間復雜度為(n+p)log(p)+nlog(n)。

5 仿真與驗證

5.1 實驗硬件架構描述與數據集描述

為了保證改進算法得到充分穩定的測試，本文使用不同規模的調度測試數據與阿里云計算中心公開的實際數據集（ALISS）進行仿真實驗。數據中心擁有10 000臺不同配置的宿主機服務器。實驗仿真硬件平臺為：曙光天闊W580-G20服務器，CPU E5-2620 v4 2.1 GHz；軟件環境為：ubuntu 18 LTS，Python3.6。

實驗的硬件架構如圖4所示。硬件架構按照功能由4種節點組成，分別為資源節點、管理節點、調度節點和服務節點。其中，服務節點負責收集云計算請求，并以集合A、S的形式提交給調度節點。管理節點負責監控資源節點的資源使用和工作情況，并以集合M的形式提交給調度節點。調度節點綜合整個云計算服務平臺的情況進行調度工作，將運算請求調度到資源節點中。

ALISS數據集中每一組數據由4張表格組成，分別是機器信息列表、應用信息列表、實例信息列表、親和與反親和信息列表。其中，機器信息列表中含有M-id、M-c、M-m、M-d，M-id為機器的ID，M-c、M-m、M-d分別對應機器集合的miCPU、miDISK、miMEM。應用信息列表中含有 A-id、A-c、A-m、A-d，A-id為應用的 ID，A-c、A-m、A-d分別對應集合中的。時變數據 CPU-use、MEM-use的采樣周期為15 min，即C=96。

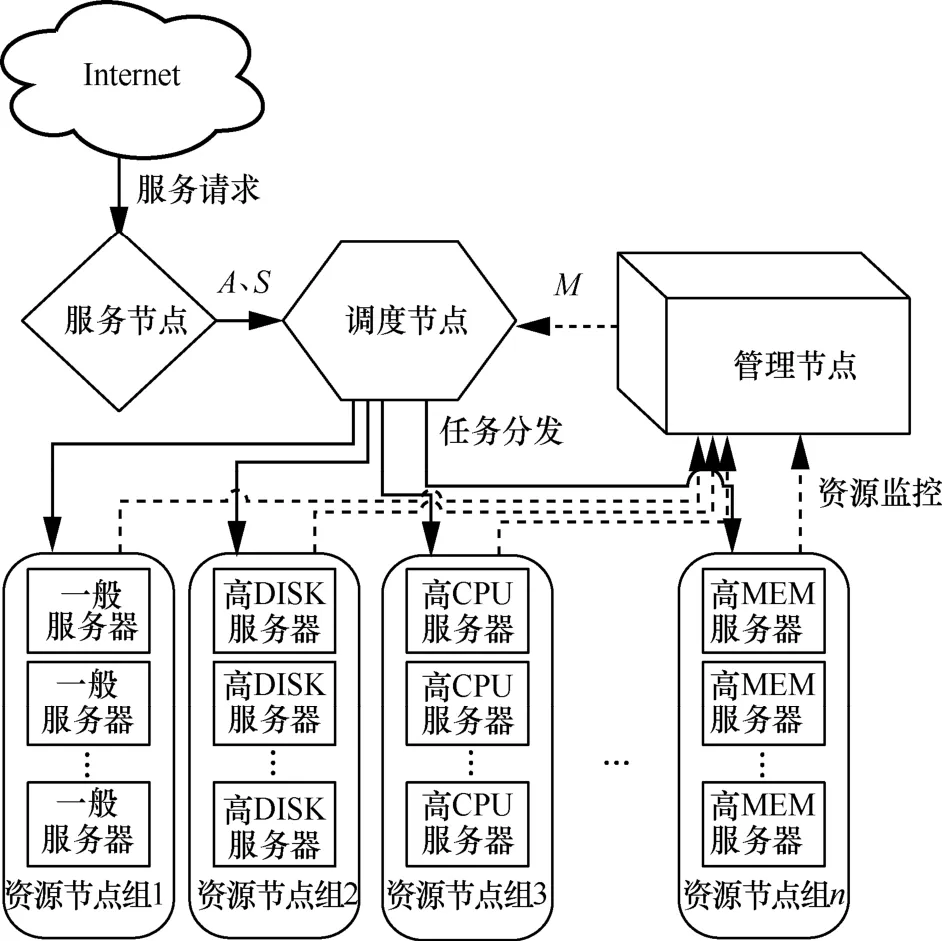
圖4 實驗的硬件架構

5.2 OTECA在ALISS上的求解結果

本節使用OTECA求解ALISS-2數據集中的調度問題。為了保證服務器運行的穩定性與資源分配的合理性，設置模型參數為α=10，β=0.5，選取OTECA參數為擇優選取集合選擇系數γ=1.5，子問題求解次數Ns=300，并對問題進行求解。求解過程如圖5～圖7所示。

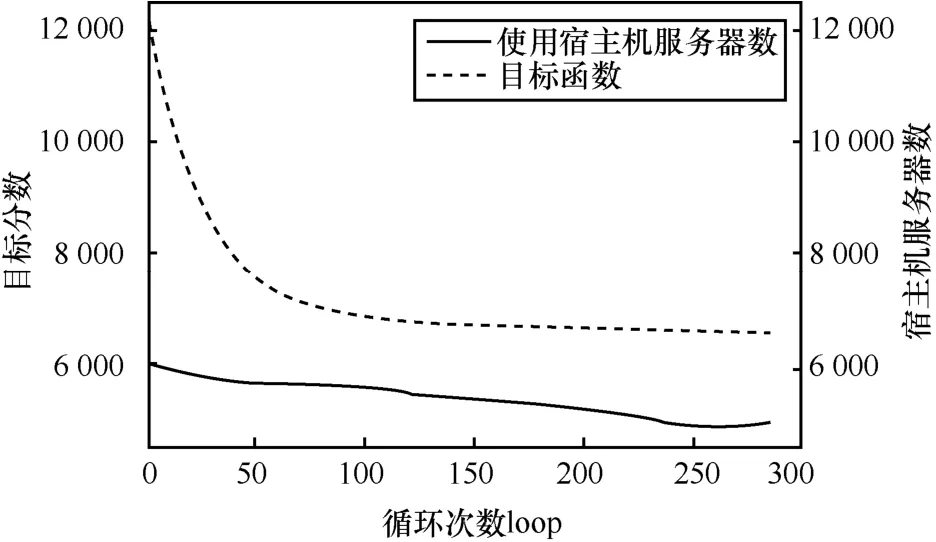
圖5 ALISS-2問題宿主機服務器數、目標函數與循環次數關系

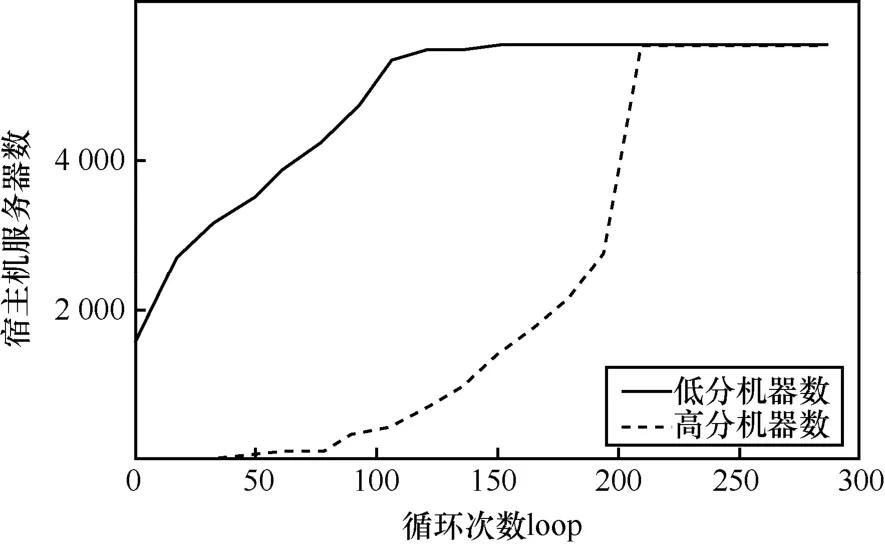
圖6 ALISS-2問題高低分機器數與循環次數關系變化

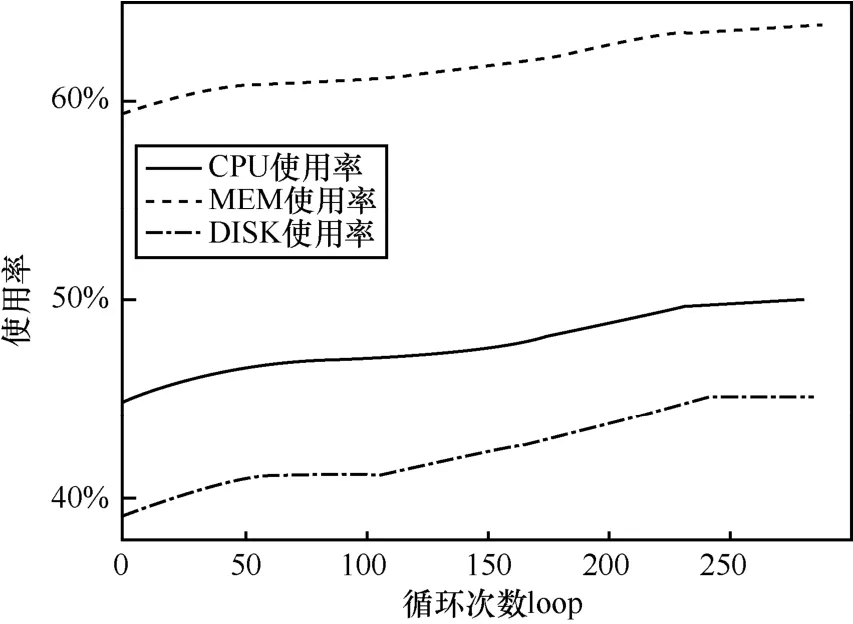
圖7 ALISS-2宿主機服務器使用率與循環次數關系變化

優化開始時，宿主機服務器平均 CPU使用率僅在45%左右，這證明優化開始時服務器組的負載并不均衡。隨著算法迭代循環次數的增加，算法將得分較高的機器中的實例與得分較低的機器中的實例使用整數規劃的方法進行最優的重新組合，重新分配到原來的機器中，并將負載進行有效的重組。由圖5可知，隨著優化的進行，得分在快速地下降。在最理想的情況下，算法將所有的機器的負載都調整到從下方逼近β的情況。由圖6可知，由于優化開始時機器分數差異較大，以最高分和最低分劃定的高分機器集合和低分機器集合中元素較少。隨著優化的進行，機器的負載逐步平均，分數的分布逐步集中，高分機器集合和低分機器集合逐漸包含同一部分機器。

當loop＞100時，由于機器的負載已經達到了平均水平，機器數與得分的差距基本不再變化，此時分數的下降主要來自機器數的削減。當某臺機器不執行任何程序時，其得分為 0。因此在交換無法使負載更加均衡的情況下，OTECA的同樣的交換操作將盡量清除多余的宿主機服務器。由圖7可知，隨著循環次數的上升，CPU的平均使用率逐漸接近β，達到接近最優解的狀態。

5.3 不同規模服務器調度問題上算法性能對比

本文在不同規模的調度問題中進行算法性能的比較。實驗算法包括 OTECA、分離化差分進化算法（C-MSDE, cost modified separation differential evolution）[23]、成本時間進化算法（CT-DE, cost time differential evolution）[24]、GA[17]和 LS[18]。

擇優選取 OTECA 中參數γ=1.5，Ns=300；C-MSDE中選擇變異因子為 1，交叉因子為 0.5；CT-DE中Ptime=Pcost=0.5；GA中選擇概率為0.2，交叉概率為0.2，變異概率為0.2；LS中搜索范圍為3；C-MSDE、CT-DE、GA的種群數為300。測試使用的服務器規格數據與云計算要求數據皆從阿里巴巴公司公布的Alibaba Cluster Data V2018中抽取，測試結果如表2所示。

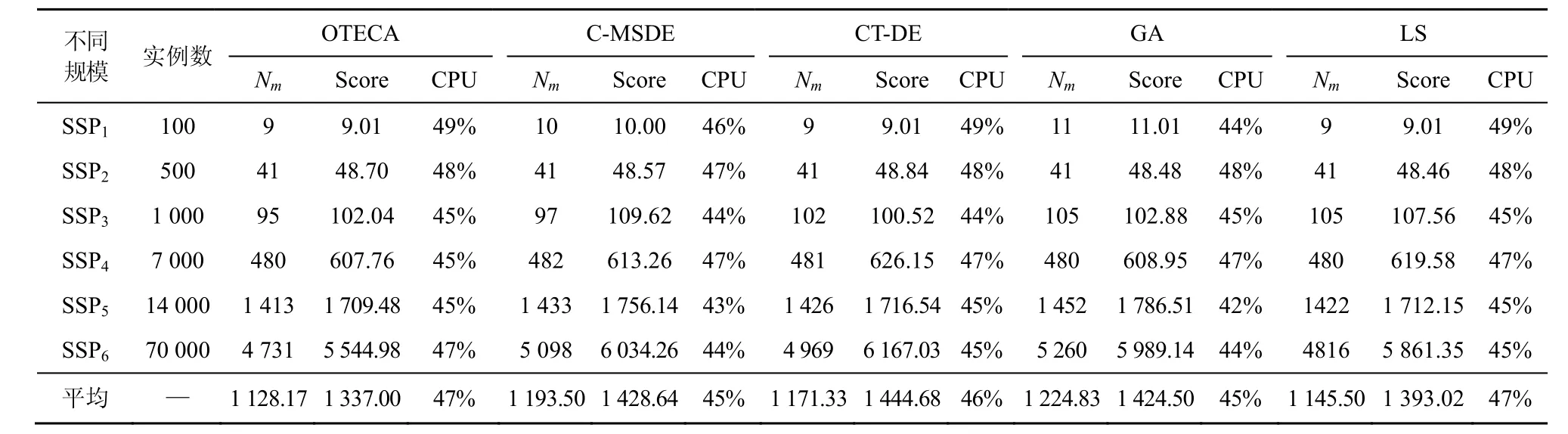
表2 不同規模服務器調度問題上5種算法性能對比

表 2中顯示了不同規模（SSP1～SSP6）的調度問題，其中SSP1～SSP3是規模與實例數較小的服務器調度問題，SSP4～SSP6是規模與實例數較大的服務器調度問題。其中，Nm代表算法調度結果使用的宿主機服務器數量，Score代表算法所得目標分數，CPU代表調度結果平均CPU使用率，目標為50%。處理小規模問題時，進行比較的算法擁有相似的性能表現，但是OTECA、CT-DE與LS擁有較好的表現，目標分數的平均值相比其他算法優秀 1%。處理較大規模問題時，OTECA展現出比較突出的性能優勢，目標分數的平均值比其他算法中最優秀的LS優秀3%。綜合上述2種情況，OTECA表現更好。

5.4 5種算法在ALISS數據集上性能對比

設置算法參數與5.3節相同，以實例在宿主機服務器中的轉移次數為橫坐標，以分數為縱坐標，得到5種算法求解ALISS-1問題如圖8所示。

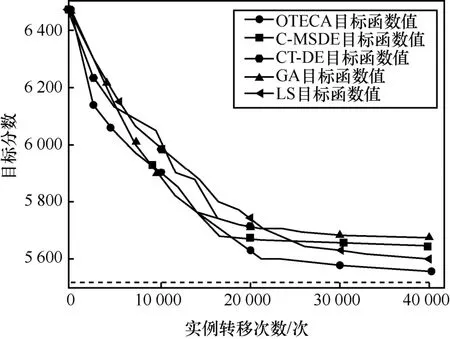
圖8 5種算法求解ALISS-1問題

圖8中最下方的虛線為該問題的最優解。在算法的初始階段，OTECA與C-MSDE的效率較高。隨著優化的進行，目標值快速下降，GA、LS與CT-DE因優化策略原因效率較低。在優化的中后階段，OTECA表現出了較強的調度能力與精確性，通過解決子問題，有目的地將組合不合理的機器挑選出來并進行重新組合，該操作在效果上優于基于隨機遷移的GA、LS、C-MSDE等其他算法，OTECA得到的調度結果能夠跳出局部最優解。

算法對服務器組負載的均衡能力是衡量算法優劣程度的重要指標，本文對于ALISS-1的求解過程繪制機器負載量直方圖，如圖9所示。

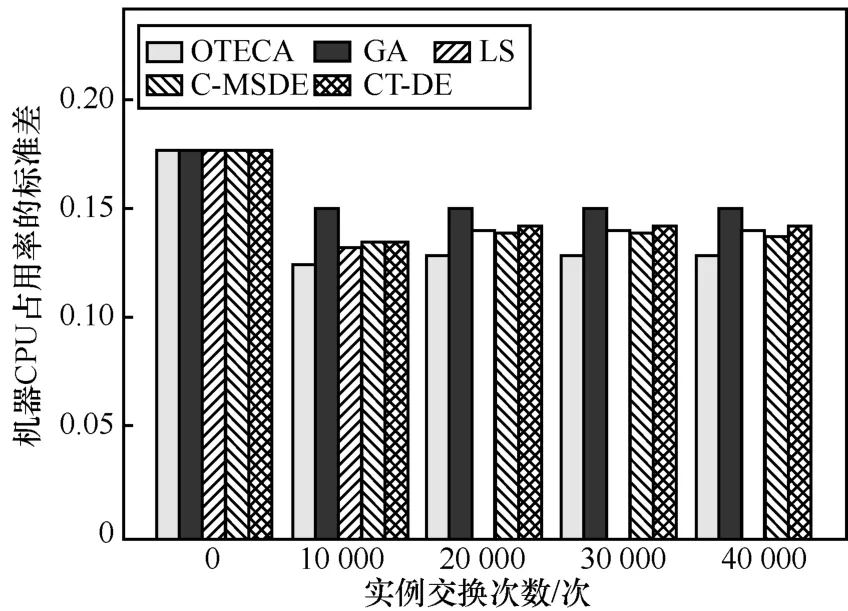
圖9 機器CPU使用率標準差直方圖

由圖9可知，當實例交換次數為0時，5種算法以相同的基礎進行優化。隨著實例交換次數的增加，5種優化方法都能起到有效的負載均衡效果。當實例的交換次數為20 000次時，OTECA的效果最為顯著，其對應的機器 CPU使用率的標準差最小，相比初始值變化的幅度是GA的2倍。隨著優化的繼續進行，其他算法的標準差幾乎沒有發生改變，而OTECA的標準差有少量提升。這是因為隨著交換的進行，OTECA能夠有效地減少使用宿主機服務器的數量，從而提高了仍在工作的宿主機服務器使用率的標準差。5種算法求解ALISS數據集的結果對比如表3所示。

表3中評價了5種算法在數據集上的5個指標，分別是目標分數（Score）、平均機器 CPU 使用率（CPU）、平均機器內存使用率（DISK）、平均機器硬盤使用率（MEM）、機器 CPU使用率標準差（STD）。在 7個測試數據中，OTECA表現最佳，目標分數的平均分為 6 665.70，比第二優秀的C-MSDE優秀4%。

數據問題的差異性會引起算法表現的差異，但是OTECA綜合性能占有一定優勢。對于ALISS-3與ALISS-4這類實例粒度較小（單個實例占用的資源較小）的問題，5種算法的表現相似。但是對于實例粒度較大的問題，GA、LS、C-MSDE與CT-DE等算法表現稍遜于 OTECA，原因是不滿足約束的情況會降低上述算法的搜索效率。綜合考慮上述情況，OTECA具有更加優秀的性能。

表3顯示，C-MSDE、CT-DE、GA與LS這4種算法在解決有相對嚴格約束的服務器調度問題時沒有明顯優勢，這是因為4種算法的解集更新具有隨機性，新生成的解很容易不滿足問題的約束。因此，檢查新解是否滿足約束與丟棄不滿足約束的解花費大量的運算時間，從而大大降低了算法性能。OTECA不需要維護多個解的集合，也從不產生可能不滿足約束的解。OTECA只通過求解 MIP子問題不斷地對解集進行更新，因此擁有較高的效率與性能。

6 結束語

本文針對大規模云服務器調度問題進行研究。在對大規模云服務器調度問題進行MIP建模的基礎上，為了解決傳統方法很難及時地求解出最優調度方案的問題，本文提出了 OTECA。OTECA首先通過可行解生成算法求出可行解，然后通過在循環中不斷選取與解決MIP子問題的方式優化可行解，從而得到全局調度方案。結果表明，OTECA可以快速優化大規模服務器調度方案，在測試數據集ALISS上較傳統的GA、LS、C-MSDE與CT-DE算法有較大的優勢。在完成相同任務的情況下，OTECA使云計算中心的資源消耗減少4%以上。

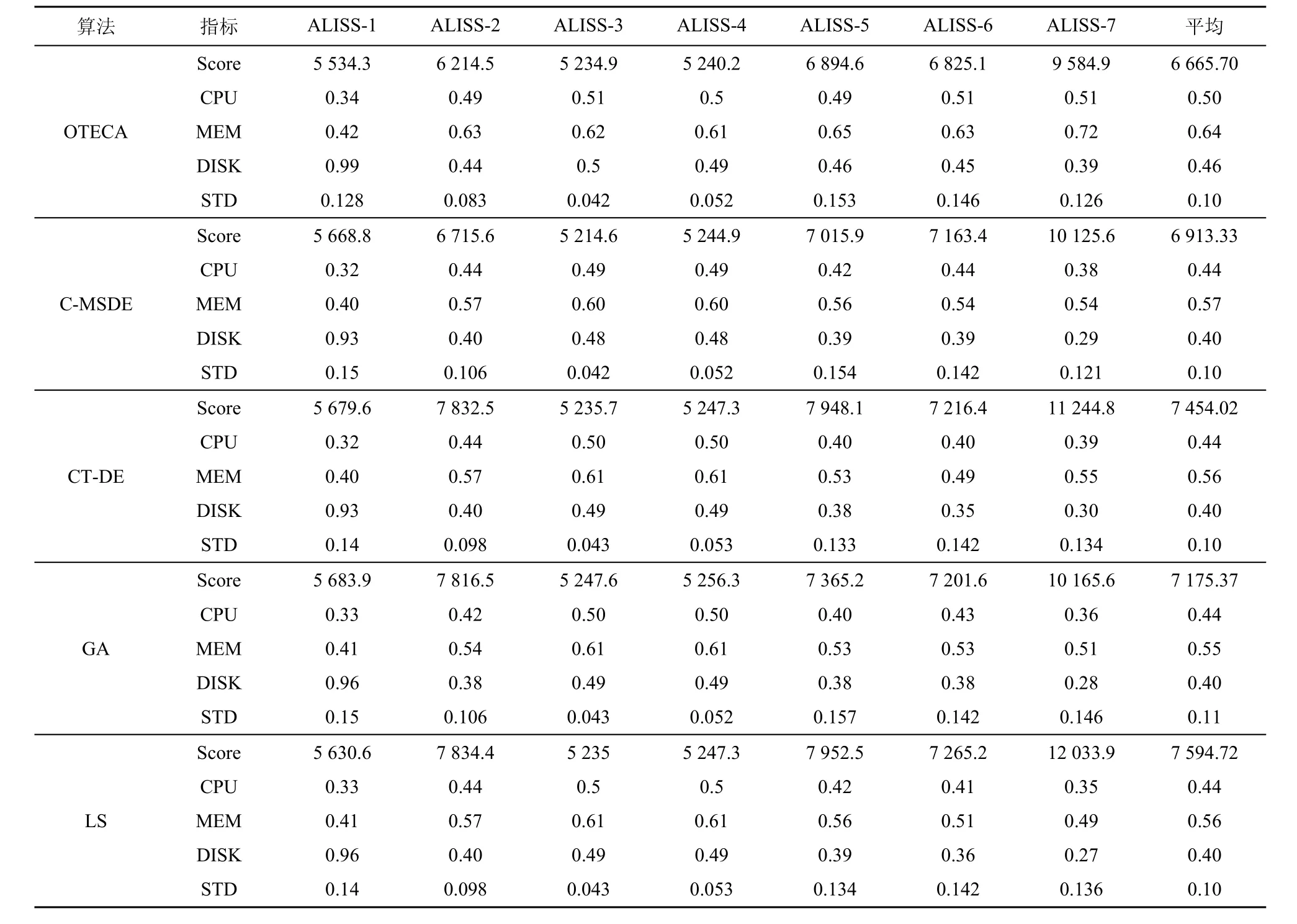
表3 5種算法求解ALISS數據集的結果對比