True-Load 載荷反求算法研究與驗證

馮建軍

摘 要：在工程結構研發設計初期如能獲取其在役載荷，將對結構的優化設計、安全可靠性、疲勞壽命和節省產品成本等具有極大的工程價值。考慮到工程結構的復雜程度和各部件間不同的傳遞和轉換載荷方式，目前通過布置應力或應變傳感器直接或間接地獲取產品結構所承受的真實載荷是很難實現的。True-Load軟件提供了一種與有限元技術相結合的解耦方法，本文以True-load提供的載荷反求算法為工具，以一段單側軌道鋼軌為研究對象對載荷反求進行了研究，對比并分析載荷反求得到的載荷數據與真實施加載荷數據的一致性;同時結合有限元分析軟件ansys進一步驗證True-load載荷反求算法的合理性和研究價值。

關鍵詞：在役載荷;True-load;軌道鋼軌;載荷數據

0 引 言

由于在役產品結構所承受的真實載荷很難準確獲得，使得研發人員僅依據經驗數據標準設計的產品性能無法滿足運行中真實的惡劣工況，尤其是隨時間變化的激勵，嚴重影響了產品結構的安全可靠性和疲勞壽命[1]。如何準確、快捷地識別和提取軌道車輛運行時的真實載荷具有深刻的理論研究價值和廣泛的工程應用背景。

當前識別與獲得軌道車輛的在戰役載主要依據經驗將應力或應變傳感器布置于車輛相關部件中以直接或間接方式測量獲得相關運行載荷，上述方法經常因為結構設計時沒有預留傳感器安裝位置而難以實現。另外考慮到載荷在車輛各部件間不同的傳遞和轉換方式，使上述方法難以準確的獲取真實載荷[2]。基于大多數工程結構系統具有應變與載荷之間存在線性關系的屬性[3-4]，國外研究人員Tim-hunter結合有限元技術研究出一款基于時間歷程的有限實測應變識別在役載荷可驗證的True-load軟件;該軟件能準確識別出時間歷程的“真實”載荷譜以及工程結構的復雜受載變化情況，對結構研發、改進設計、疲勞耐久性分析以及問題重現等問題研究具有深遠意義。

本文以True-load提供的載荷反求算法為工具，以一段單側軌道鋼軌為研究對象進行了載荷反求研究，對比并分析載荷反求得到的載荷數據與真實施加載荷數據的一致性。同時結合有限元分析軟件ansys進一步驗證True-load載荷反求算法的合理性和研究價值。

1 基本算法簡介

1.1 基本算法

1.2最佳應變片貼片位置

根據應變與外載荷之間線性關系，結合精確的有限元模型求得的相關矩陣 ? ? ，經過線性變換構建矩陣 ? ? ? ?并基于試驗設計的D-Optimal優化準則可得當矩陣 ? ? ? ?行列式最大時確定應片最佳位置和角度[5-6]。

2 單側軌道鋼軌載荷反求有限元驗證

下面通過軟件True-load提供的線性系統載荷反求算法并結合有限元分析軟件ansys16.0，以單側軌道鋼軌為研究對象，驗證True-load提供的解耦算法的合理性。

2.1 ?創建有限元模型及施加載荷工況

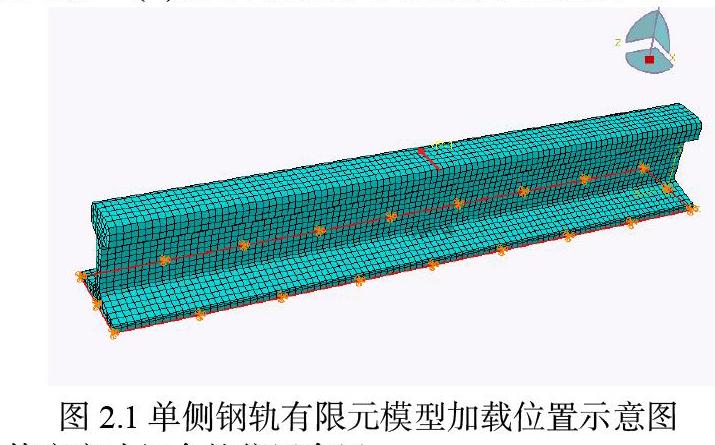
首先建立一定長度的單側軌道鋼軌模型。鋼軌有限元模型主要以六面體單元網格構成，鋼軌表面創建一層用于提供布置應變片位置的2D膜單元。在有限元模型施加與實際實驗情況一致的載荷和邊界位移條件，本研究對象鋼軌對軌頭施加X方向集中應力Fx =10kn的載荷，Fx 按周期為20秒的正弦函數sin（ct）隨時間變化。其加載位置如如下圖2.1所示。

2.2 ?最佳應變片組合的位置布置

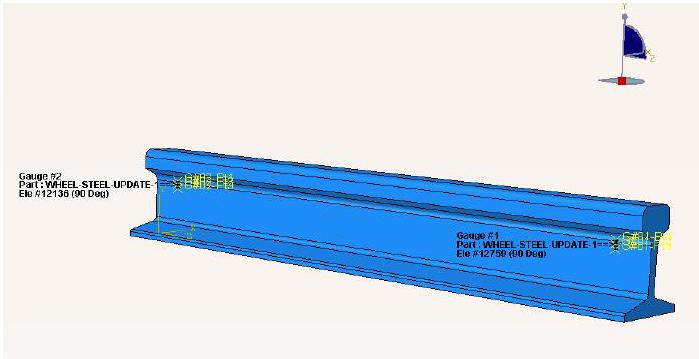
選取易于貼片位置的膜單元，依據軟件中D-Optimal優化準則與計算的條件數值來選取試驗應變片數量以及確定最優貼片位置和角度。本實驗確定的最優應變群包括2個應變片，其位置如下圖2.2所示。

2.3 ?反求載荷數據及對比

本實驗通過matlab軟件對實際施加與True-load反求得到的X方向載荷數據進行處理，將上述兩組數據擬合成兩條正弦函數曲線如下圖2.3所示。計算數據與實驗測得數據相關系數R為0.9346，剩余平方和SEE為0.232. 上述表明反求計算載荷與實際施加的載荷存在一定的差距。

查找兩種載荷數據不一致的原因，重新檢查載荷反求各個環節，依次確認建模、載荷約束施加、試驗平臺載荷施加方法均準確，同時true-load軟件前、后處理步驟和后期試驗數據處理均無誤。最后發現應變片粘貼位置和角度沒有按軟件D-Optimal優化算法確定的方位完全執行。

在ansys軟件中創建幾何形狀相同且更加精細的單側鋼軌有限元模型，將Fx 按照激勵正弦函數sin（ct）在一個周期（20秒）內分散成30個離散的點，即在有限元模型上添加30個離散點數值的X方向的載荷Fx 。分別計算并提取出D-Optimal算法重新求出的兩個最優應變片位置的30次應變值，匯編成相應的試驗載荷譜，最后應用于True-load軟件載荷反求后期處理中。經過matlab軟件同樣的數據處理得下圖2.4。從兩曲線相關擬合度可得反求計算載荷值與實際施加的載荷值基本一致（其R為0.986，SEE為0.102）。進一步表明了true-load載荷反求精確程度與有限元網格大小（即精細程度）、最優應變片位置密切相關，同時驗證了True-load載荷算法具有一定的合理性和有待深層次理論研究的現實價值。

3 載荷反求原理科學性的反思

反思本文載荷反求過程和對比分析實驗數據后，發現合理的應變片最佳布置位置是值得考慮的問題。雖然True-load采用D-Optimal （行列式值最大化）算法的本質是從已經布置的、離散的應變片貼片樣本點數據中剔除出某些應變片使行列式值逐漸增大，這在數學上只是一種準則，沒有較強的物理背景，而問題越復雜，越難保證初選的應變片貼片位置（坐標）的集合中一定含有最合理的位置 （坐標）。本文所述的載荷反求實驗假設了一個相對簡單的實驗載荷，通過對比實測數據和ansys仿真載荷譜數據后對D-Optimal算法求出最優解的唯一性產生了質疑，有待進一步探討。

4 結論

本文以一定長度的單側鋼軌為研究對象，基于軟件True-load的優化算法進行了載荷反求實驗，本文實驗雖然僅研究了一個相對簡單的問題，但通過實驗過程和處理相關數據后可知：（1）實驗有限元建模必須逼真;（2）嚴格執行軟件D-Optimal優化算法確定的最優應變片方位。

結合當下有限元發展 的程度，精細建模可以解決上述第一個問題;考慮到工程結構復雜程度和實驗機構貼片水平，第二個問題也不難實現。在滿足上述兩個條件時，True-load軟件反求工程結構外載荷可以獲取較為真實的載荷，同時拓寬了載荷反求思路，具有一定的工程應用價值。

參考文獻（References）

[1]王勖成，邵敏.有限單元法基本理論和數值方法[M].清華大學出版社，1997.

[2]云利軍，孫鶴旭，雷兆明，等.運動控制網絡的研究現狀及發展趨勢[J].控制工程，2006，23（04）：289-293.

[3]Kwak. Jin Ho， and Sungpyo Hong. Linear Algebra. Boston： Birkhauserl， 1997. Print.

[4]Timothy. G. Hunter. Wolf Star Technologies Training. Dalian， 2015.

[5]Fabian Triefenbach. Design of Experiments： The D-Optimal Approach and Its Implementation As a Computer Algorithm[D]. Umea University of Sweden.. 2008.

[6] Wickham M J， Riley D R， Nachtsheim C J， et al. Integrating Optimal Experimental Design into the Design of a Multi-Axis Load Transducer[J]. Journal of Engineering for Industry， 1995， 117（3）：400-405.