基于VISUM交通仿真和OD矩陣反推技術的交通預測模型研究

文/王中立 重慶交通大學 土木工程學院 重慶 400074

張沈越 武漢理工大學 汽車工程學院 湖北武漢 430070

1、緒論

1.1 問題提出

交通需求預測，是交通規劃的核心內容之一[1]。早在上個世紀，西方發達國家在大規模城市道路交通規劃和建設過程中，逐漸形成了“四階段”城市道路需求預測技術。四階段（four-step）模型是指將需要完成的交通需求預測任務劃分為四個子任務，即交通產生量預測、OD分布預測、交通方式分擔預測和交通量分配預測。

“四階段”技術在長期的城市交通規劃實踐中得到了檢驗，自該方法誕生之日起，其框架幾乎沒有發生變動，方法簡單可靠，但“四階段”技術依賴大規模的城市交通普查，在當今城市人口流動極其頻繁的情況下，交通普查的成本和難度越來越大，其精度也不容樂觀。同時，其傳統預測模型難以反映社會發展，城市交通管理政策變化的影響，也無法考慮到周邊環境隨時間序列推移，對各交通小區出行的連鎖反應。

1.2 研究內容

文章對交通擁堵進行判定，闡述交通擁堵產生的原因，收集了目前應對交通擁堵的方法，介紹了現有交通運行狀況評價體系。同時，文章還對宏觀交通仿真技術進行闡述，介紹了宏觀交通仿真軟件VISUM，提出了OD矩陣反推與交通預測模型相結合的思路。

研究以VISUM交通仿真軟件上的Oppidum小鎮為研究樣本，將研究范圍按用地情況和道路的自然分割劃分為67個交通小區，查詢得到的1960-2000年城市主干道年交通量。通過對1960-1999年數據分析處理，預測出2000年交通量。

2、宏觀交通仿真機理

2.1 宏觀交通仿真的定義

根據研究范圍及對象的不同，交通仿真通常被分為宏觀交通仿真、中觀交通仿真和微觀交通仿真 [2]。

宏觀交通仿真要求采集路段速度和流量，相較于中觀交通仿真和微觀交通仿真，對交通實體、交通信號等細節要求比較低。在宏觀交通仿真過程中，研究者以OD矩陣為主要研究對象，對交通基礎設施建設和遠景規劃進行科學分析，如公交線路的優化、評價新建公路影響。

2.2 研究概況

交通仿真現狀的發展分成三個階段，20世紀60年代，研制了TRANSY、SIGOP等系統，但由于當時計算機發展不夠好，仿真系統也并不完備。后來，隨著計算機的發展，仿真模型迅速發展，出現了MISTRAN模型、SATURN宏觀模型等[3]。到20世紀80年代，ITS的研究熱潮襲來，各國相繼研制了各種不同，應對不同情況和路段的仿真模型。到目前，交通仿真系統分為宏觀和微觀，微觀的有CORSIM、PARAMICS和VISSIM，而宏觀的有VISUM。傳統的微觀分析方法適用的范圍、影響因素較小的情況，而宏觀的交通仿真軟件如VISUM以整體為目標，研究特定問題，分析路網情況，對交通流量進行分析分配，從而實現科學規劃，減少擁堵情況。VISUM現已經用于對于路網的分析，為城市道路的規劃提供依據[4]。

2.3 基于大數據交通仿真技術的城市交通量組合預測模型

交通仿真軟件的出現在很大程度上促進了交通的發展，是交通領域的一座里程碑。隨著社會的發展，影響交通的相關因素越來越多，應用計算機技術進行交通仿真就成為了一種很有效的技術手段。交通仿真不僅可以復現交通流時空變化的技術、為交通道路設計規劃提供技術依據，而且還可以對各種參數進行比較和評價，以及環境影響的評價等。但是，交通是一個很復雜，又很巨大的一個體系，由于軟件自身的局限性，往往在算法預測上不夠精確，對交通狀態的描述顯得不夠完善，因此，文章考慮將引入OD矩陣反推后的卡爾曼濾波模型應用于交通仿真軟件VISUM，提出一種解決交通擁堵問題的新思路[5]。

3、卡爾曼濾波預測模型

3.1 模型提出背景

卡爾曼濾波是一種高效率的遞歸濾波器，是一種建立在最小方差估計的基礎上的算法，利用線性系統狀態方程，輸入觀測數據，再對系統進行最優估計。[6]

3.2 算法詳述

將實際觀察到的交通量數據，經過一系列運算反推出歷史的OD矩陣，再運用卡爾曼濾波模型，運用方程對得到的OD矩陣進行處理，預測得到新的結果[7]。這樣就將卡爾曼濾波模型與交通量結合起來，實現對OD矩陣的處理和運用。

以極大熵OD反推模型：

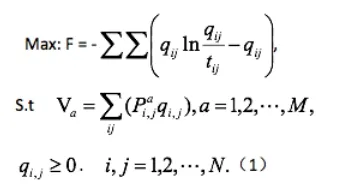
對于上述極大熵模型，由于其目標函數的特殊性，直接求解難以進行，通常用拉格朗日乘子法將其化為如下非線性方程組的形式：

上述方程組是含有M+1個變量和M+1個方程的非線性方程組，通過求解上述未知數即拉格朗日乘子，然后由（1）式求出OD矩陣，則有下式：

對于上述線性方程求解，采用數值解法。

4、現狀交通分析

4.1 傳統方法

卡爾曼濾波模型在交通需求預測中的應用，首先要根據交通流量時間和空間的相關性選擇狀態變量的個數。其基本有五個公式，簡單介紹如下。

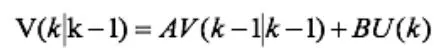
T表示協方差：

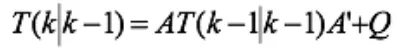
結合預測值和測量值，可以得到現在狀態(k)的最優化估算值V(k|k) ：

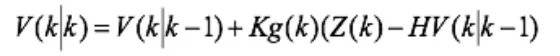
Kg為卡爾曼增益：

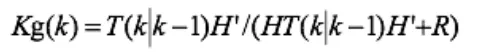
現在，得到了k狀態下最優的估算值V(k|k)。為了使卡爾曼濾波器不斷的運行下去直到系統過程結束，還要更新k狀態下V(k|k) 的協方差即：

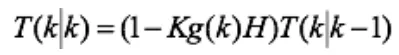
假設在k時刻某觀察點的車輛數與k-1、k-2時間段都有一定關系和聯系，根據這個關系，可以預測同一地點在k+1時刻的交通流[9]。

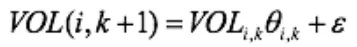
經過一系列處理和遞推可以得到：

得到對比結果（圖1）：

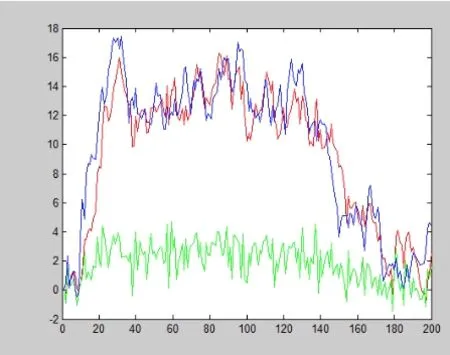
圖1 MATLAB圖像

其中，紅色為卡爾曼濾波，綠色為量測，藍色為狀態。得出根據卡爾曼濾波模型預測出的交通流量，再與實際流量對比，我們可以看出卡爾曼濾波模型對于預測的準確性和及時性情況[10]。通過加權計算絕對誤差，我們發現預測值與實際值有10.56%的誤差。

4.2 基于組合模型的交通分析

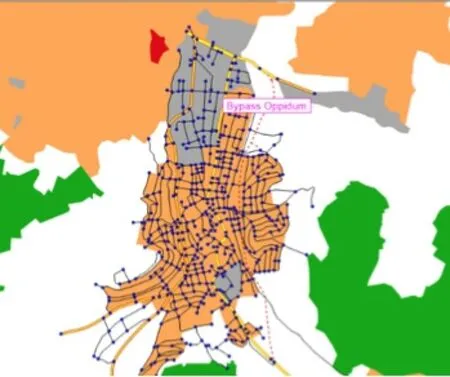
圖2 Oppidum小鎮路網圖

在VISUM軟件中，首先將Oppidum小鎮分為67個交通小區（圖2），并自動生成小區連接線，生成40個以極大熵OD反推模型為主要原理的OD反推矩陣，并存入數據庫，接著，將1960-1999年的Oppidum小鎮OD交通需求矩陣通過卡爾曼濾波交通需求預測，得出預測值，即2000年各路段交通量，與實際數據對比，通過加權平均算出絕對誤差為5.11%。

4.3 傳統四階段法與組合模型的比較

與傳統的"四階段"技術相比，以極大熵原理為基礎的OD反推算法與卡爾曼濾波模型相結合的方法的預測更加簡便和高效。同時，與真實值相比，傳統方法預測誤差為10.56%，文中組合模型誤差為5.11%，文中方法更加精確。

結論：

通過對傳統交通流量需求預測四階段法的改進，提出以歷史交通流量基礎，用VISUM軟件中Oppidum小鎮的數據，以極大熵模型反推出OD矩陣，再利用卡爾曼濾波模型對OD矩陣進行處理和預測，最后將預測出的OD矩陣輸入VISUM仿真軟件中進行重新分配。在新的預測方法中，將OD矩陣反推的極大熵模型和卡爾曼濾波模型結合起來，形成更優的組合模型，省去了傳統方法中大量的交通調查，節省大量物力財力和時間，同時還提高了預測精度。本文提出的方法在精準性、可靠性、簡便性、可行性方面都有一定優勢，為今后更加有效的規劃交通，更簡便、精準的解決城市擁堵問題提供理論基礎。