受正弦擾動的線性系統的無靜差控制?
林 華, 宿 浩, 唐功友
(中國海洋大學信息科學與工程學院, 山東 青島 266100)
在實際應用中,幾乎所有的控制系統都會受到來自外部的擾動信號。系統的外部擾動往往使得控制系統的性能明顯減弱,甚至使閉環系統無法正常工作。在實際系統中,具有正弦特性或周期性特性的擾動是很常見的擾動形式,如飛機飛行振動控制系統[1]、海洋平臺振動實時控制系統[2]、工業噪聲減振控制、汽車振動減振控制系統等都是在具有正弦特性或周期性特性的擾動下工作的。因此,研究如何減弱或者抑制外部擾動信號對控制系統性能的影響,對實際工程實踐有重要的意義。
對于受擾系統的擾動抑制問題,通常前饋反饋算法較經典的反饋控制有更好的擾動抑制效果,例如文獻[3]針對正弦擾動的控制系統,給出了一種前饋反饋的擾動抑制算法。前饋控制的缺點是需要增加擾動傳感器實時測量擾動信號。對于已知頻率、未知振幅和初相角的不可測量的正弦擾動,或其它不可測量的恒值擾動,比較有效的擾動抑制控制方案包括自適應控制[4-5]和預測控制[6-7]等,這些方法對于具有持續擾動(如正弦擾動)的抑制在一定范圍內都會存在不同程度的靜差。基于內模原理的控制器設計可以保證閉環系統實現無靜差擾動抑制,目前利用內模原理主要是針對擾動的不穩定模態設計擾動抑制控制器[8-9]。文獻[10]利用內模原理設計了一種受正弦擾動的系統的無靜差擾動抑制控制器,這種控制器要求正弦擾動是可測量的,控制器中包含了前饋控制的分量。
本文針對受外部持續正弦擾動的n階線性系統,提出了一種設計無靜差擾動抑制控制器的設計方法。設計的動態狀態反饋控制器具有二階動態特性。通過設計控制器中的n+2個參數,可以使閉環系統的極點任意配置,從而保證了閉環系統的指數漸近穩定性。利用內模原理,通過在控制器中嵌入正弦擾動的模態矩陣,保證了閉環系統的無靜差擾動抑制。
1 問題描述
考慮受正弦擾動的線性系統
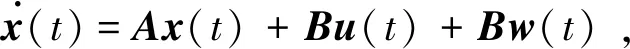
(1)
式中:x∈Rn、u∈R、w∈R分別是狀態向量、控制輸入和擾動輸入;x0是初始狀態向量;A,B為適當維數的常量矩陣,假設矩陣對(A,B)是完全能控的。不失一般性,可將系統(1)描述為能控規范型形式,即
(2)
假設外部擾動w(t)為正弦特性:
w(t)=asin(ωt+b)。
(3)
式中:頻率ω是已知的,振幅a和初相位b是未知的。并假設外部擾動w(t)是物理不可測量的。
在實際系統中,由公式(3)描述的外部擾動是普遍存在的,如工業生產過程中,來自50 Hz工頻干擾的電壓信號,其頻率是已知的,但初相位和干擾的振幅是未知的。
本文的研究目的是對于由公式(1)描述的線性系統,如何設計反饋控制律,實現對正弦擾動公式(3)的無靜差擾動抑制。
2 無靜差控制律的設計
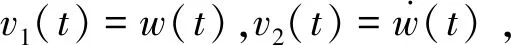

(4)
式中
(5)
對于傳統的內模原理設計方法,總是考慮在閉環系統內嵌入系統擾動或系統參考輸入的不穩定的模態,其目的是抵消系統外部輸入的不穩定模態引起的閉環系統的穩態誤差。基于內模原理的設計方法,本文試圖在閉環系統中嵌入純虛數極點模態,并提出設計鎮定控制器的設計方法。
我們設計如下動態控制律:
(6)
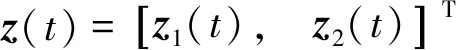
將動態控制律(6)代入系統(1),得到系統(1)的閉環系統:
(7)
圖1示出了閉環系統(7)的結構圖。
我們的目的是設計2×n矩陣H和n階行向量k使得:
(I)閉環系統(7)的極點可以任意配置,即可使閉環系統(7)漸近穩定,且當擾動w(t)≡0時,狀態向量x(t)可以以任意預先給定的指數速率趨向于0。
(II)當擾動w(t)由(3)描述時,閉環系統(7)可以實現無靜差擾動抑制,即:狀態向量x(t)滿足:
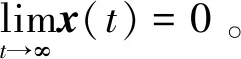
(8)
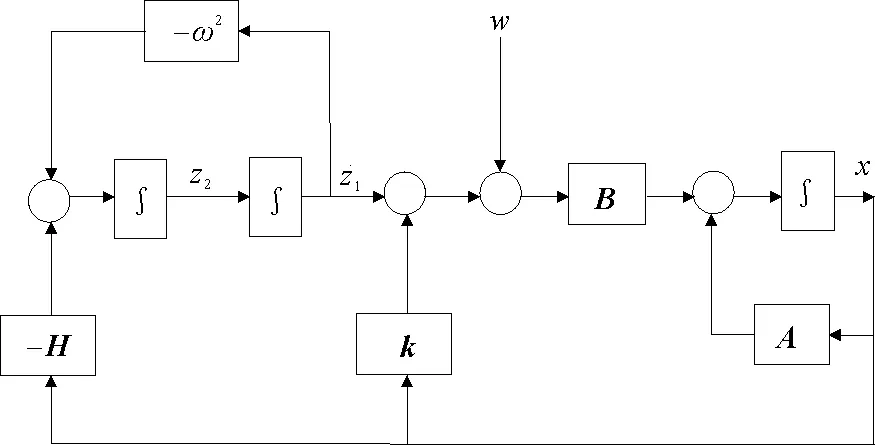
圖1 系統結構圖Fig.1 System structure diagram
由公式(7)可知,閉環系統是一個(n+2)階系統。我們知道,要使閉環系統(7)的極點可以任意配置,在控制律公式(6)的2×n矩陣H和n階行向量k中,至少要有(n+2)個自由分量可供我們設計。又要使控制律(6)的結構盡量簡單,我們希望控制律公式(6)的2×n矩陣H和n階行向量k中分量可供我們設計的自由分量個數越少越好。依據這一設計原則,我們選擇2×n矩陣H和n階行向量k的結構為:
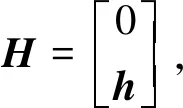
(9)
k1,k2和hi(i=1,2,…,n)為待定的常數。
我們先給出主要結果:
定理1設計受正弦擾動(3)的線性系統(1)的動態反饋控制律公式(6)。適當選擇控制器參數k1,k2和hi(i=1,2,…,n),閉環系統公式(7)的極點可以任意配置。
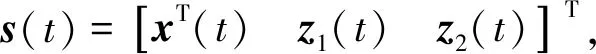

(10)
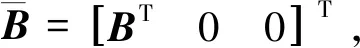
(11)
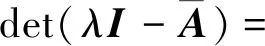
λn+2+(k2-an)λn+1+(ω2+k1-an-1)λn+
[hn+ω2(k2-an)-an-2]λn-1+
[hn-1+ω2(k1-an-1)-an-3]λn-2+
(hn-2-ω2an-2-an-4)λn-3+…+(h3-ω2a3-a1)λ2+
(h2-ω2a2)λ+(h1-ω2a1)。
(12)
預先給定閉環系統公式(10)的(n+2)個極點λi(i=1,2,…,n+2),則有:
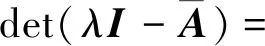
(13)
其中:
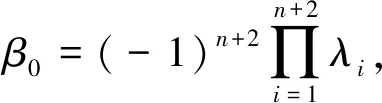

(14)
比較公式(12)和(13)等號右邊λ的同次冪系數,得到:
hn+ω2(k2-an)-an-2=βn-1,
hn-1+ω2(k1-an-1)-an-3=βn-2,
hn-2-ω2an-2-an-4=βn-3,
…
h3-ω2a3-a1=β2,
h2-ω2a2=β1,
h1-ω2a1=β0,
k2-an=βn+1,
ω2+k1-an-1=βn。
(15)
求解(15)得:
hn=an-2-ω2βn+1+βn-1,
hn-1=an-3+ω2(ω2-βn)+βn-2,
hn-2=an-4+ω2an-2+βn-3,
…
h3=a1+ω2a3+β2,
h2=ω2a2+β1,
h1=ω2a1+β0,
k2=an+βn+1,
k1=an-1-ω2+βn。
(16)
綜上分析,只要按(16)選取控制器參數k1,k2和hi(i=1,2,…,n),則閉環系統(10)的極點可以任意配置。
推論1設計受正弦擾動(3)的線性系統(1)的動態反饋控制律(6)。適當選擇控制器參數k1,k2和hi(i=1,2,…,n),如果系統擾動w(t)≡0,閉環系統(7)可以是指數漸近穩定的,且狀態向量x(t)可以以任意預先給定的指數速率趨向于0。
證明 令系統擾動w(t)≡0,則閉環系統(10)可以寫為:
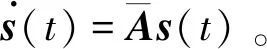
(17)
類似于定理1的證明,預先給定閉環系統(17)的(n+2)個具有負實部極點λi(i=1,2,…,n+2),按(16)設計控制器參數k1,k2和hi(i=1,2,…,n),則閉環系統(7)是指數漸近穩定的。不妨令
(18)
顯然,閉環系統(17)的解滿足:
(19)
式中M是足夠大的正常數。又由于是任意給定的具有負實部的常數,所以且狀態向量x(t)可以以任意預先給定的指數速率趨向于0。
注1:定理1的證明不僅證明了閉環系統(10)的極點可任意配置,而且給出了動態反饋控制律公式(6)的參數k1,k2和hi(i=1,2,…,n)的選取公式(16)。
定理2設計受正弦擾動(3)的線性系統(1)的動態反饋控制律公式(6)。按公式(16)選取控制器參數k1,k2和hi(i=1,2,…,n),則閉環系統公式(7)關于狀態向量x(t)是漸近穩定的,從而實現對系統公式(1)的無靜差擾動抑制,即公式(8)成立。
證明 令
ei(t)=vi(t)+zi(t),i=1,2。
(20)
由(4)和(7)得:
(21)
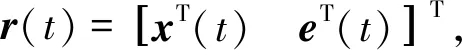
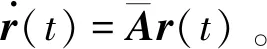
(22)

注2: 由定理2不僅說明了利用受正弦擾動(3)的線性系統(1)的動態反饋控制律公式(6)可以實現無靜差擾動抑制,而且給出了動態反饋控制律公式(6)的參數k1,k2和hi(i=1,2,…,n)的選取公式(16)。
3 示例仿真
考慮受正弦擾動(3)的3階線性系統(1),其中:
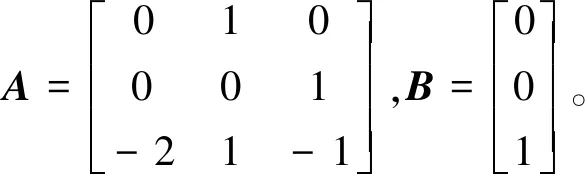
假設系統的輸出為y(t)=x1(t)。系統的初始條件為:
x1(0)=x2(0)=x3(0)=0,
a=2,b=0。
以下作者利用本文提出的動態控制律算法公式(6)與狀態反饋控制律對該系統的控制效果進行比較。在兩種控制律控制效果的討論中,假設選擇狀態反饋控制閉環系統的極點為:
s1=-1+j,s2=-1-j,s3=-2。
狀態反饋控制律及設計過程從略。
設計動態控制律公式(6),由公式(11)得閉環系統公式(7)的系數矩陣為:
本文分2種情形討論動態控制律公式(6)的控制效果。
給定閉環系統公式(7)的(n+2)=5個極點:
s1=-1+j,s2=-1-j,s3=-2,s4=-3,s5=-4。
則由公式(12)、(13)和(14)得:
β0=48,β1=100,β2=94,β3=46,β4=11。
再由公式(16)得到控制器參數:
h3=92-11ω2,
h2=ω2(ω2-46)+100,
h1=-2ω2+48,
k2=10,
k1=-ω2+47。
圖2示出了ω=0.5π時的系統仿真曲線。
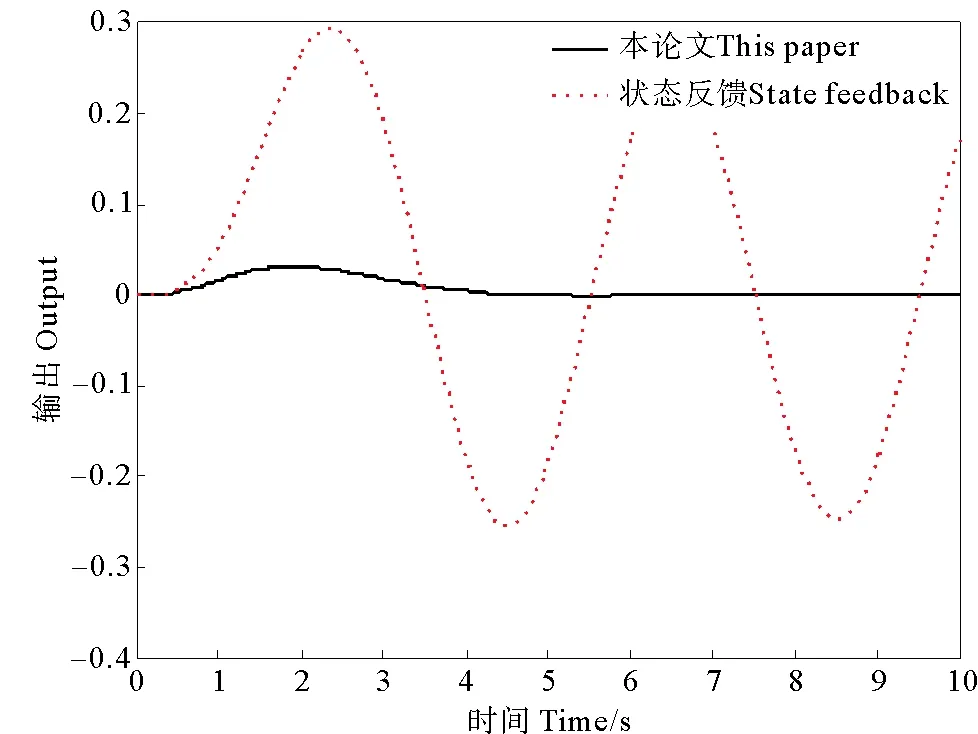
圖2 ω=0.5π時的系統仿真曲線Fig.2 Simulation curves of the system when ω=0.5π
圖3示出了ω=π時的系統仿真曲線。
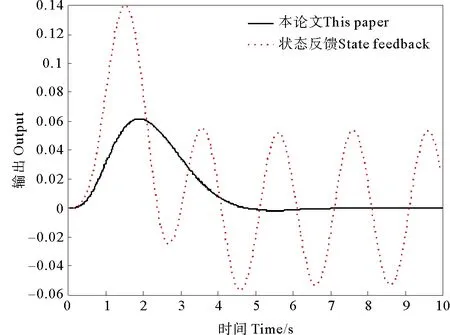
圖3 ω=π時的系統仿真曲線Fig.3 Simulation curves of the system when ω=π
圖4示出了ω=1.5π時的系統仿真曲線。

圖4 ω=1.5π時的系統仿真曲線Fig.4 Simulation curves of the system when ω=1.5π
圖5示出了ω=2π時的系統仿真曲線。

圖 5 ω=2π時的系統仿真曲線Fig.5 Simulation curves of the system when ω=2π
從圖 2~5 中可以看到,不論外部正弦擾動信號的頻率如何,利用本文提出的控制器算法,都能使閉環系統的響應逐漸趨于0。正弦擾動信號的頻率越低,控制效果越好。但是利用本文設計的控制律,閉環系統的響應曲線的超調量會隨著正弦擾動信號頻率的增加而增加。在列舉的仿真例子中,當正弦擾動信號頻率ω>1.5π時,閉環系統的響應曲線的超調量會迅速增大。而僅利用狀態反饋控制律,閉環系統的響應曲線都不能使閉環系統的響應逐漸趨于0。 但會隨著正弦擾動信號頻率的增加而增加,閉環系統的響應曲線的振蕩幅值越來越小,這說明利用狀態反饋控制的閉環系統有低通濾波的特性。
綜上分析表明,本文設計的擾動抑制控制律能使閉環系統指數漸近穩定,而且在正弦擾動下能夠實現無靜差擾動抑制。本文的控制器設計方法特別適合于具有較低振蕩頻率的正弦擾動的系統。
4 結語
本文基于內模原理研究了輸出反饋擾動抑制控制律的設計問題。本文設計的擾動抑制控制律能使閉環系統指數漸近穩定,而且在正弦擾動下能夠實現無靜差擾動抑制。仿真結果表明,本文的控制器設計方法僅適用于具有較低振蕩頻率的正弦擾動的系統,正弦擾動的振蕩頻率越低,閉環系統的動態性能越好。

