基于馬氏距離的重采樣方法在流量識別中的應用?
時鴻濤, 李洪平, 劉 競
(中國海洋大學信息工程學院, 山東 青島 266100)
精確的網絡流量識別是流量工程、網絡安全、網絡質量服務(QOS)以及用戶行為分析等工作的基礎[1]。由于動態傳輸技術、流量加密算法和隧道技術在互聯網中的廣泛應用,傳統的基于端口號和有效載荷檢測的流量識別技術變得不再準確和高效,因此人們提出了基于機器學習的流量識別算法[2]。這類算法通過分析和識別流量底層的統計特征來實現網絡流量的識別。由于不需要分析流量的有效載荷信息,這類算法的計算性能和準確率都非常高。目前,基于機器學習的流量識別方法已經成為了網絡流量研究的重點。然而,隨著研究的深入,人們發現網絡流量中數據分布的不均衡問題會嚴重影響流量識別的準確率。這種不均衡通常會導致機器學習算法偏向于流量數據中多數類的流量樣本。例如:文獻[3]指出網絡流量數據中HTTP流量的數量通常會遠遠超過P2P和VoIP流量的數量,而機器學習算法通常會將所有流量識別為HTTP流量以實現高準確率。在這種情況下,機器學習算法對于少數類流量的識別準確率非常低。然而,在許多情況下這些少數類流量(例如P2P和VoIP流量)卻是人們更加關心的。
目前,解決數據分布不均衡問題的方法可以主要地分為兩個方向:數據層方法和算法層方法。數據層方法主要通過對不均衡數據中的少數類進行過采樣或者對多數類進行欠采樣來實現數據的均衡。文獻[4]提出了一種新的過采樣方法SMOTE(Synthetic minority over-sampling technique),該方法能夠通過合成新的樣本來提高少數類樣本的比例。文獻[5]提出了一種邊界SMOTE過采樣方法,該方法通過對邊界附近的少數類樣本進行過采樣來實現樣本的均衡。文獻[6]通過比較過采樣方法和欠采樣方法,指出過采樣方法在解決數據分布不均衡問題時比欠采樣方法更加有效。此外,算法層方法主要通過調整與錯誤分類相關的偏差來解決數據分布不均衡問題。文獻[7]通過使用樣本加權方法來構建成本敏感決策樹(Cost-sensitive decision tree)以解決數據分布不均衡問題,并且該方法被證明能夠非常有效的解決數據分布不均衡問題。文獻[8]比較了成本敏感方法和重采樣方法在解決數據分布不均衡問題的效果,結果顯示成本敏感方法能夠實現與重采樣方法相似的效果。然而,以上方法雖然取得不錯的效果,但這些方法主要用于二分類的數據分布不均衡問題,對于網絡流量中的多分類數據分布不均衡問題,現有的重采樣方法往往存在過擬合的缺點,而成本敏感方法則由于難以獲得準確的錯誤分類偏差從而導致較低的識別準確率。
本文針對以上存在的問題,提出了一種基于馬氏距離的重采樣算法,該方法能夠兼顧數據分布結構和變量間的相關性。因此所生的樣本能夠保留原始數據分布特征,并最大程度地避免過擬合的發生。
1 算法模型
1.1 馬氏距離度量方法
馬氏距離是由印度學者馬哈拉諾比斯提出的一種距離度量方法,該方法能夠有效的計算兩個向量之間的相似度距離。相比歐氏距離,馬氏距離能夠考慮到向量中各變量之間的相關性。歐氏距離是一種普遍采用的距離度量方法,它被定義為n維空間中兩個向量之間的幾何距離,其計算公式如下:
(1)
也可以通過向量運算形式來表示:
(2)
歐氏距離的特點是計算向量之間的平均幾何距離,即向量中每個變量對于歐氏距離的貢獻是相同的。然而,在統計學中人們更傾向于根據向量中每個變量的方差來評估變量間的距離,并且具有較大方差的變量在距離計算中將具有較高的權重。因此,馬氏距離度量更能體現這一統計特性。馬氏距離的計算公式可表示如下:
(3)
式中:S為樣本集的協方差矩陣;因此,馬氏距離能夠兼顧數據分布特征和變量之間的相關性。值得注意的是,當協方差矩陣S為單位矩陣時,馬氏距離可簡化為歐氏距離。
1.2 主成分分析介紹
主成分分析是一種的多元統計方法,它能夠在降低數據維度的同時盡可能的保留原始數據中的大多數變量信息。該方法主要通過線性轉換將一組存在相關性的變量轉換為一組線性無關的綜合變量,這些轉換后的綜合變量被稱為主成分。主成分分析的公式可表示如下:
C=AX
。
(4)
式中:X為樣本數據矩陣;A為主成分系數矩陣;C為主成分向量,且主成分之間相關性為零,即Cov(Ci,Cj)=0 (Ci,Cj∈C,i≠j)。因此,主成分之間的協方差矩陣可表示為一個對角矩陣V,其公式如下:
V=λE。
(5)
式中:λ是主成分的特征值向量,E為單位矩陣。
此外,為了簡化原始數據,在選擇主成分數量時通常會選擇一個主成分集合的子集來代表原始變量。通常主成分個數的選擇需要根據所選主成分的方差累計貢獻率G來決定。
(6)
式中:λ為各主成分的特征值;s為所選擇的主成分數量;n為全部主成分數量。當方差累積貢獻率G>85%時,就認為所選擇的前s個主成分能夠反映原始變量的信息。
1.3 基于馬氏距離的重采樣方法
本文所提出的基于馬氏距離的重采樣方法將根據少數類中每個樣本點與樣本集中心之間的馬氏距離來生成新的合成樣本。由于馬氏距離計算的復雜性,本文先利用主成分分析將原始樣本數據轉換到主成分空間,再通過計算各樣本點到樣本集中心的馬氏距離來實現新樣本的生成。主成分空間下馬氏距離的計算公式可簡化為
(7)
即:
(8)
本文將利用公式(8)來實現樣本數據的重采樣,整個算法流程如算法1所示。基于馬氏距離的重采樣算法主要包含以下幾個步驟:
(1)對輸入的樣本數據進行零均值化處理(代碼1)。
(2)使用主成分分析方法將零均值化后的樣本數據轉換至主成分空間,并選擇方差累積貢獻率G>85%的主成分子集作為原始變量的代表以簡化計算復雜度(代碼2)。
(3)在主成分空間中循環生成新樣本(代碼3)。首先,隨機選擇一個樣本數據p,計算它到樣本集中心的馬氏距離dM(p,0)(代碼3.1),然后,定義一個新的樣本數據q,并使該樣本數據滿足條件dM(q,0)=dM(p,0)(代碼3.2)。
(4)使用主成分分析方法將生成的新樣本集合轉換至原始數據空間(代碼4)。
(5)通過逆零均值化得到最終數據結果(代碼5)。
(6)對所有新樣本數據進行輸出(代碼6)。
算法1基于馬氏距離的重采樣算法
輸入:Sin={(x1,1,x1,2,…,x1,m),…,(xn,1,xn,2,…,xn,m)} %少數類樣本集合,
k%需要生成的新樣本數量,
輸出:Sout%新生成的樣本集合。
1:forj=1 tomdo
end for
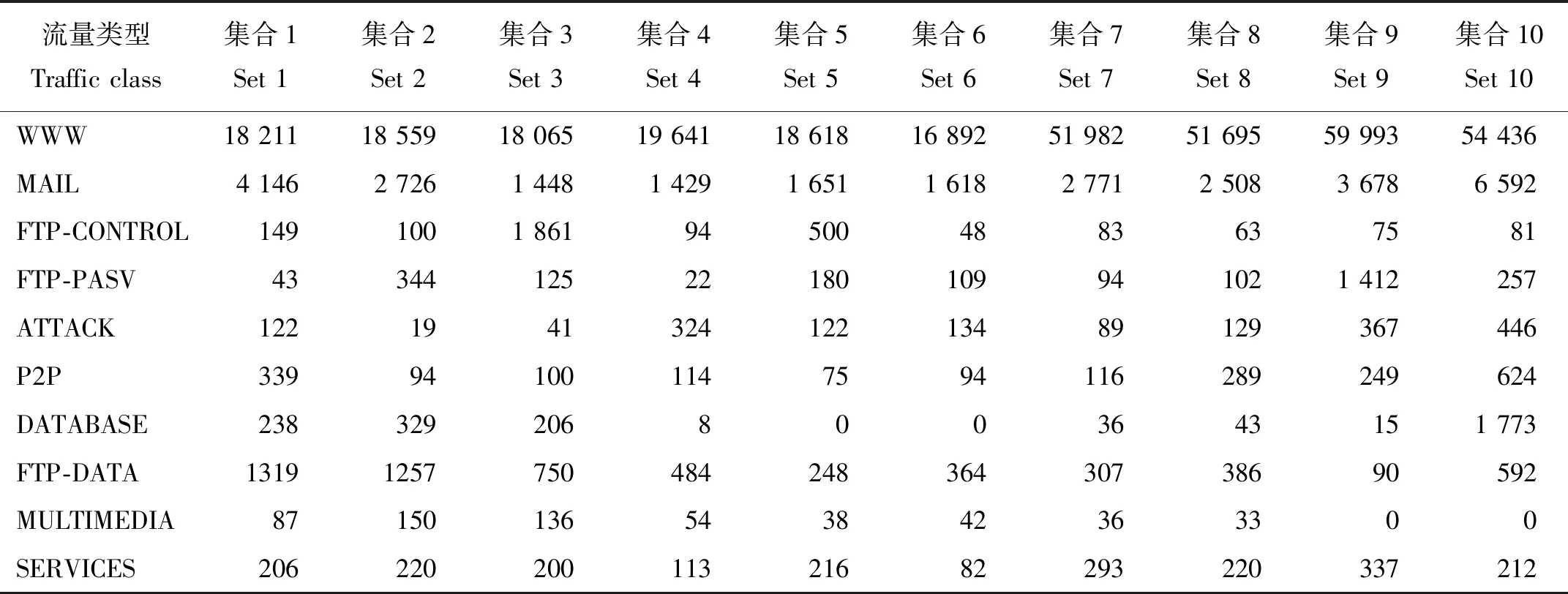
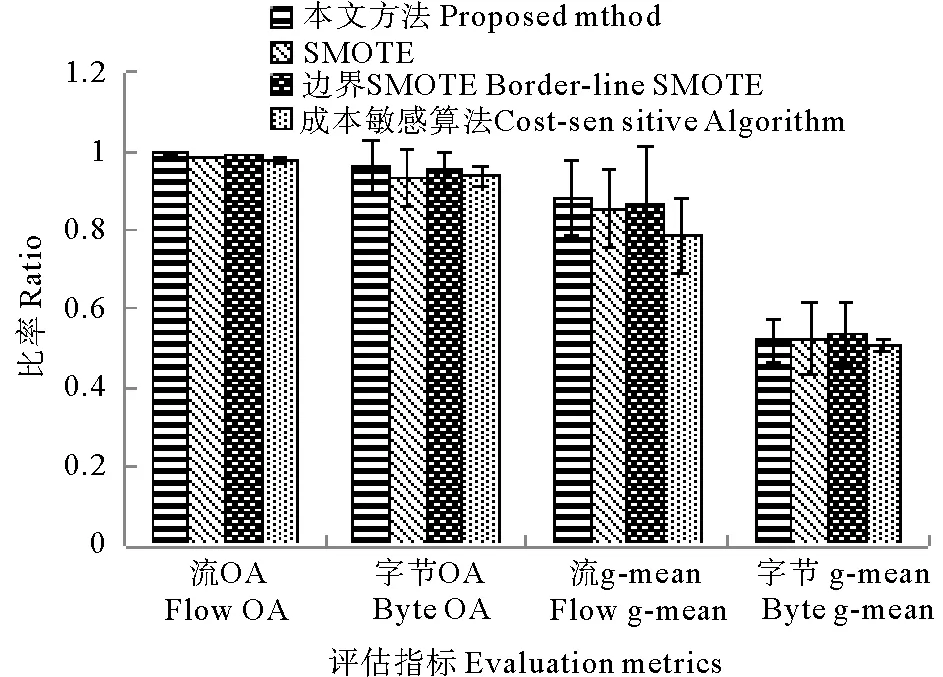
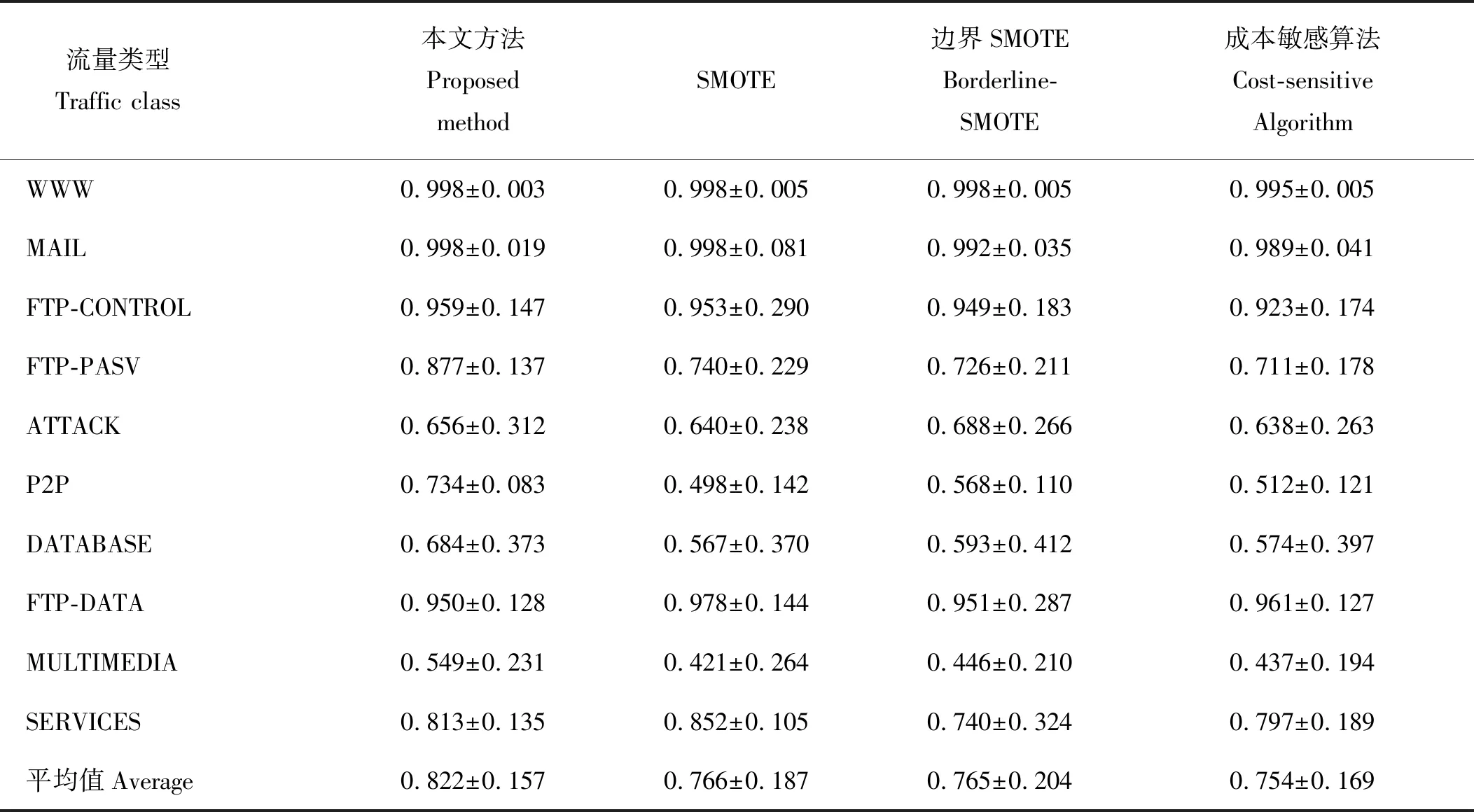
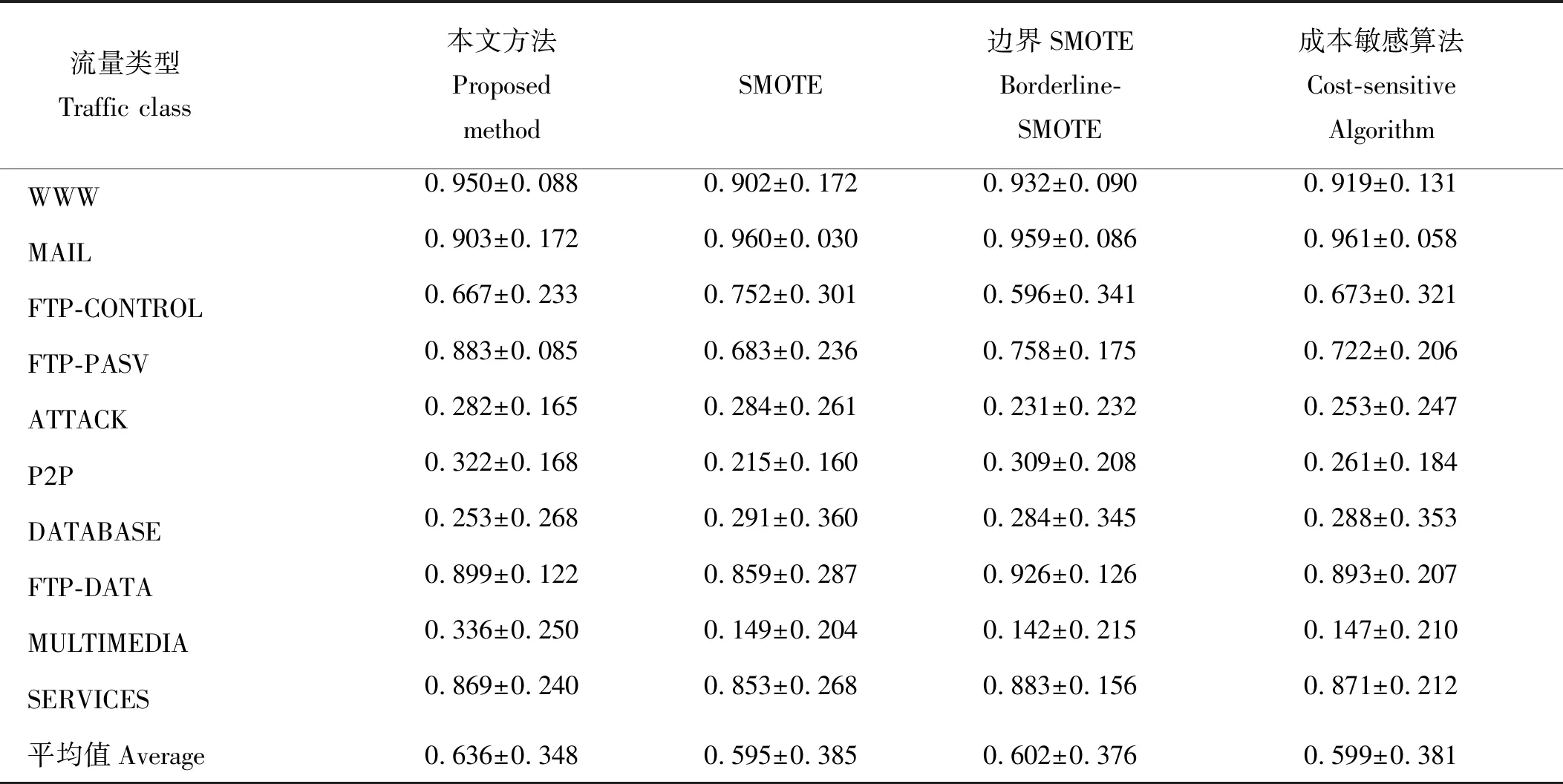
2:計算Z的主成分,并選擇G>85%的主成分子集T,其行數和列數分別為n和m1(m1 3:fori=1 tokdo 3.1:p=random(T) 3.2:定義q forj=1 tom1-1 do %為q前m-1項賦值。 qj=random(-λ1dM,λidM) end for 將q加入集合Tnew。 end for 4:將Tnew轉換至原始數據空間,得到新集合Znew。 6:返回Sout。 通過以上算法,所有新生成的樣本將與原始樣本保持相同的數據分布特征。下面將通過實驗來驗證本文算法的效果。 為了檢驗本文提出的重采樣方法,本文使用劍橋大學實驗室提供的公共網絡流量數據[7]作為實驗數據。這些網絡流量數據包含10個數據集合,每個集合包含有不同數量的網絡流量樣本。每個樣本具有248個特征,這些特征是通過使用Tcptrace進行提取。實驗數據的流量特征信息如表1所示。從表1中可以發現對于所有集合,WWW流量類型的樣本數量遠遠超過其他流量類型。因此,這些數據集都存在明顯的多分類數據分布不均衡問題。 表1 實驗數據特征信息Table 1 The characteristic information of the experimental data 為了評價所提出方法的有效性,本文使用3種不同的評價指標對分類結果進行分析。這些評價指標包括總體準確率(Overall Accuracy, OA)、F-measure和g-mean。這些指標通常被用于評價信息分類和檢索的效果。 令TP代表真陽,TN代表真陰,FP代表假陽,FN代表假陰。OA可以表示為被正確分類的樣本數量與全部樣本數量之間的百分比,它反映了分類結果的總體正確程度,OA越高表示被正確分類的樣本數量越多,其公式如下: (9) F-measure是召回率R和精確率P的一種加權平均值,它表示了對分類結果中的查準率和查全率的綜合評價,F-measure越高表示分類算法更加有效: (10) g-mean表示為所有類型流量召回率的幾何平均值,它主要用于評估多分類分布不均衡數據的分類效果,g-mean越高表示對少數類的分類效果越好: (11) 式中n為網絡流量類型的數量。 在本文中,所有指標將分別按照網絡流量數據的流(Flow)和字節(Byte)兩種方式進行計算以評估本文方法的性能。 本文選用C4.5決策樹作為分類算法,使用數據集1作為訓練數據,并對其余9個數據集進行分類實驗。為了證明本文方法的有效性,本文方法將與文獻[2]中的SMOTE方法,文獻[3]中的邊界SMOTE方法以及文獻[8]中的基于MetaCost的成本敏感算法進行比較,總體實驗結果如圖1所示。通過對圖1的觀察,我們發現本文方法對于流OA、字節OA和流g-mean都獲得了最佳分類結果,然而對于字節g-mean,本文方法的性能略低于其他方法。此外,我們發現在本實驗中邊界SMOTE方法的實驗結果要優于SMOTE方法,這與文獻[3]中的結論一致。相比之下,成本敏感算法得到了最差的實驗結果。 圖1 總體實驗結果Fig.1 Overall experimental results 表2詳細顯示了4種方法對于各流量類型所獲得的流F-measure。通過表2不難發現本文方法對于大多數流量類型均取得了最佳的流F-measure,而對于ATTACK和FTP-DATA流量類型,本文方法所取得的流F-measure也接近于相應的最佳流F-measure。此外,通過對表3中最后一行所顯示的平均流F-measure進行分析,可以證明本文方法獲得了最佳的流分類效果。 表3詳細顯示了4種方法對于各流量類型所獲得的字節F-measure。與表2類似,本文方法對于大多數流量類型,特別是含有大象流(Elephant flow)的流量類型(如:P2P和FTP-Data流量類型),均獲得了最佳的字節F-measure。此外,通過對表3中最后一行所顯示的平均字節F-measure進行分析,可以證明本文方法獲得了最佳的字節分類效果。 表2 4種方法對于各網絡流類型所獲得的流F-measureTable 2 The flow F-measure of the four methods for each traffic class 通過對全部實驗結果進行分析,可以發現本文方法在處理網絡流量中的多分類數據分布不均衡的問題時,其性能明顯優于現有的重采樣方法以及成本敏感方法,這也充分證明了本文方法在生成新的少數類樣本時能夠充分保留原始數據中的數據分布特征,從而最大程度地避免破壞原始樣本數據的數據結構。 表3 4種方法對于各網絡流類型所獲得的字節F-measureTable 3 The byte F-measure of the four methods for each traffic class 本文提出了一種基于馬氏距離的重采樣方法,該方法能夠根據樣本數據到樣本集合中心點之間的馬氏距離為少數類生成新的合成樣本。相比于現有的重采樣方法,本文方法在為少數類生成新樣本的同時,能夠保持樣本數據的原始分布結構,從而避免過擬合的發生。使用劍橋大學實驗室提供的公共網絡流量數據進行流量分類實驗,實驗結果證明與現有的SMOTE方法、邊界SMOTE方法以及基于MetaCost的成本敏感算法相比,本文方法能夠更好的提升少數類的分類準確率,從而實現最佳的流量分類效果。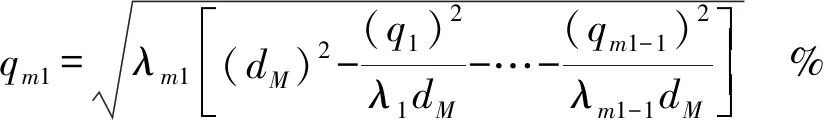
2 實驗分析
2.1 實驗數據
2.2 評估指標
2.3 分類結果分析
3 結語

