如何找到思維的開竅點

陜西省咸陽師范學院基礎教育課程研究中心 安振平

1．問題呈現

筆者看到，唐秀穎先生主編的《數學題解辭典（平面解析幾何）》（上海辭書出版社，1983，06）一書的第38題為：

問題1-1：已知三平行線l1，l2，l3．l1與l2之間，l2與l3之間的距離分別為a，b．正△ABC的三頂點分別在l1，l2，l3上．求此正三角形的邊長．

這道經典的題目，通過加工，竟然出現在2007年四川高考理科卷上．

問題1-2：如圖1，l1，l2，l3是同一平面內的三條平行直線，l1與l2間的距離是1，l2與l3間的距離是2，正△ABC的三頂點分別在l1，l2，l3上，則△ABC的邊長是（ ）

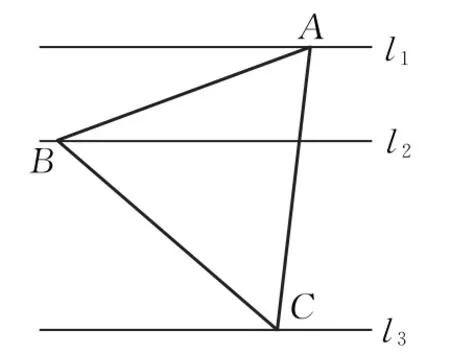
圖1

2．解題分析

本考題條件簡明，情境設置獨特，不少考生望而生畏，不知如何求解．

解題思維的起點，來自于深度的理解題意，翻譯題意，實施文字語言、圖形語言和符號語言的轉化．把平行直線“l1與l2間的距離是1，l2與l3間的距離是2”顯示為圖形語言，就需要作出題目中平行線的垂線段，垂線段作在哪里呢？

分析1 設出正三角形的邊長，通過勾股定理，建立方程．

解法1 如圖2，過點A作AF⊥l3交l2于點E，交l3于點F，過點B作BD⊥l3交l3于點D．則AE=1，BD=EF=2．

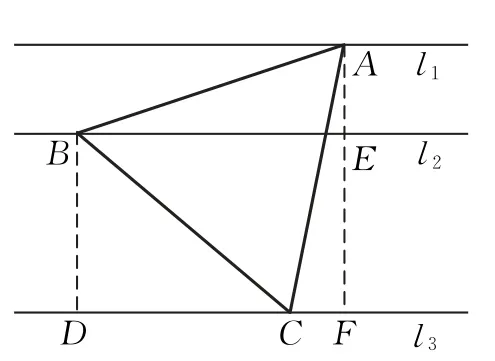
圖2

設正△ABC的邊長為x．

對Rt△BCD，Rt△ACF和Rt△ABE，應用勾股定理，得

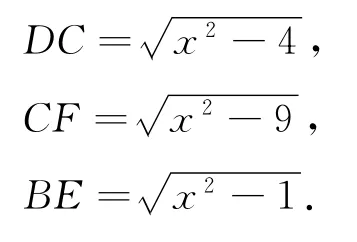
注意到DC+CF=DF=BE，

這是一個無理方程，如何求解呢？化無理為有理，平方技巧啊！

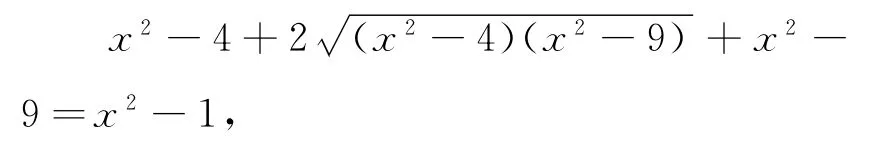
整理得

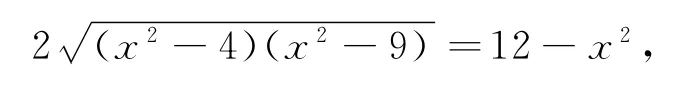
對上述方程兩邊平方，得

4（x2-4）（x2-9）=（12-x2）2，

整理為標準的一元二次方程，有

3x4-28x2=0．

說明 本解法用到的知識僅局限于初中范圍，設元，構造方程，把無理方程轉化為有理方程，檢測了考生的基本運算能力．當中的“平方兩次”的技巧，這是高中教材“橢圓標準方程”的推導過程中用過的方法．當然，本方程也可以探究其他的技巧解答方法，留給讀者去完成．

解題思維的要害、開竅點在哪里呢？同一條線段DF的長度“算兩次”．對三個直角三角形，應用了三次“勾股定理”．

分析2 設出正三角形的邊長和圖2中Rt△ABE的一個內角，通過銳角三角函數的定義，建立方程組．

解法2 如圖2，設正△ABC的邊長為x，∠ABE=θ，則∠EBC=60°-θ=∠BCD．

對Rt△ABE，Rt△BCD，應用銳角三角函數的定義，有

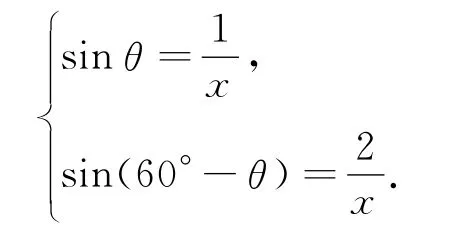
對這個方程組，為求邊長x，可以先求sinθ的值，為此，先消去x，得

sin（60°-θ）=2sinθ，

3（1-sin2θ）=25sin2θ，

說明 本解法在列方程組時，僅用到初中范圍的知識，但解答需要用到高中的三角公式．巧妙設出角度，應用方程組的觀點，借助三角恒等變形，代數運算量要簡單一些．

解題思維的要害、開竅點在哪里呢？在于巧設角度和邊長兩個變量！對兩個直角三角形，兩次應用了“正弦的定義”．

分析3 從圖3中兩個直角三角形的相似，設出正三角形的邊長，而后應用余弦定理、三角形面積公式構造方程，通過方程方法求解之．

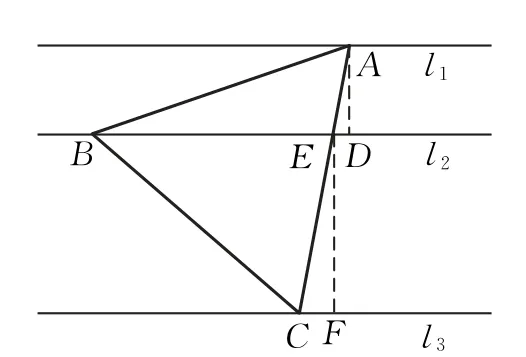
圖3

解法3 如圖3，過點A作AD⊥l2于點D，過點E作EF⊥l3于點F．則AD=1，EF=2．

顯然Rt△ADE∽Rt△EFC，則有

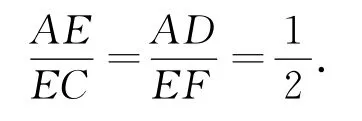
設AE=x，則EC=2x，正△ABC的邊長為3x．

對△ABE，應用余弦定理，有

BE2=AB2+AE2-2AB·AE cos 60°，

下面研究△ABC的面積：

一方面，

另一方面，

說明 本解法在計算三角形面積時，既用到小學教材里的三角形面積公式，又用到了高中教材里的三角形面積公式，這是最為核心的基礎知識．

解題思維的要害、開竅點在哪里呢？同一個三角形的面積，從不同角度“算兩次”，就自然獲得了需要的方程．

看來，在用條件的過程里巧設、妙列，才可能簡單求解．當中，“設、列、解”，值得玩味！

3．變式思考

思考1 對上述解法1里獲得的方程，給出類似的問題，就有：

問題2-1：解方程

思考2 把問題2-1里的“根號”改為“絕對值號”，并將“等號”改為“不等號”，就有：

問題2-2：解不等式|x-3|+|x-2|≤|x-1|．

思考3 如果把問題2-1左面的“根號”改為“絕對值號”，就有：

問題2-3：解方程|x-3|+|x-2|=

對于問題2-3，也許你會立即“觀察”出它有一個根2！大膽猜想之后，還需要小心求證．還有其他根嗎？且行且思．

思考4 更進一步，通過變式探究，還可以獲得：

問題2-4：求方程|x-2|+|x-1|+|y|=3表示的曲線所圍區域面積．

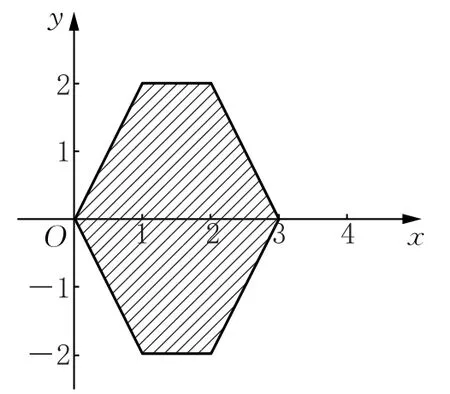
圖4

解 由|x-2|+|x-1|+|y|=3和0≤|y|，得|x-2|+|x-1|≤3，解得0≤x≤3．

當y≥0時，方程|x-2|+|x-1|+|y|=3轉化為函數

顯然，方程|x-2|+|x-1|+|y|=3表示的曲線關于x軸對稱．于是，可以畫出該方程表示的整個曲線，其所圍區域的面積

說明 發現了方程表示曲線的對稱性，從“方程”變更為“函數”就顯得那么自然，區域的“直觀”呈現就水到渠成．

數學解題，需要邏輯推理，需要數學抽象，需要構造模型，更需要代數變形和幾何直觀．轉化的功力是解題能力的具體呈現，把陌生問題熟悉化，復雜問題簡單化，未知問題已知化．正如上文中的“無理化有理”“幾何化三角”“絕對值化分段”等等．

我們可以從這樣的分析問題、發現問題、提出問題和解決問題的“修煉”過程中，體驗數學學習的奇妙，感悟數學思維的味道．