小學數學核心內容群：本質解析與教學設計

武麗莎

?

小學數學核心內容群：本質解析與教學設計

武麗莎

（唐山師范學院 數學與信息科學系，河北 唐山 063000）

小數數學核心內容群，即在小學數學的三個學習領域（數與代數、圖形與幾何、統計與概率）內，能夠聯結相應領域中不同學段的小學數學內容并為其提供持續性支持、具有奠基作用的數學知識結構和數學思想方法。小數數學核心內容群具有聯結性特征、持續性特征、奠基性特征、思想性特征，從數學學科發展以及數學本質的角度解析核心內容群有助于小學數學教學策略的設計與教學資源的開發。

小學數學核心內容群；本質解析；教學設計

1 小學數學核心內容群的內涵

1.1 何為“核心”

《現代漢語詞典》對“核心”一詞的解釋為中心，即主要部分[1]。所謂“核心”，是指在一定的領域或體系中，對事物或事情的存在提供支持和持續作用、某類領域或體系中不可或缺的部分，既可以是現實世界的存在物，也可以是精神世界的存在物。從范圍層面來看，“核心”一定是針對某個領域或者體系而言，以孤立形態存在的對象沒有“核心”；從時間層面來看，“核心”對事物或事情存在的支持具有持續性，其支持作用不會消失；從功能層面來看，“核心”是不可或缺的，是一個領域或體系存在的前提，具有一定的奠基作用。

1.2 何為小學數學核心內容群

數學內容是數學知識與數學思想兩條主線的集中體現[2]，缺少數學知識的數學內容沒有價值，缺少數學思想的數學內容沒有靈魂，數學知識發生發展的過程就是數學思想形成凸顯的過程。小學數學內容作為數學內容的下位概念，一方面應該具備數學內容的共同屬性，另一方面又具有反映自身的特殊性。《義務教育數學課程標準（2011年版）》（以下簡稱《課程標準（2011年版）》）指出：“在數學課程中，應注重發展學生的數感、符號意識、空間觀念、幾何直觀、數據分析觀念、運算能力、推理能力和模型思想。為了適應時代發展對人才培養的需要，數學課程還要特別注重發展學生的應用意識和創新意識。”[3]

基于“核心”和小學數學內容兩方面因素，我們提出小學數學核心內容群的概念，它是包括知識點、綜合數學知識結構和思想方法的內容體系，具有基礎性、聯結性、持續性、思想性等特征。所謂小數數學核心內容群，即在小學數學的三個學習領域（數與代數、圖形與幾何、統計與概率）內，能夠聯結相應領域中不同學段的小學數學內容并為其提供持續性支持具有奠基作用的數學知識結構及其蘊含的數學思想方法。

2 小數數學核心內容群的數學本質解析

2.1 小學數學“數與代數”領域核心內容群

2.1.1 數與數量

人類很早便具有區分數量的能力，數的形成依賴于對現實世界中數量本質的抽象，但是從這種對數量的感性認知抽象到對數的理性認知卻是緩慢漸進的，這種理性認知的對象便是某種群組所共有的屬性（數）[4]。“數概念的形成可能與火的使用一樣古老，大約是在30萬年以前，它對人類文明的意義也決不亞于火的使用。”[5]而記數是伴隨著計數的發展而發展的，十進制記數系統經歷了計數、符號兩個層次的抽象過程[6]。

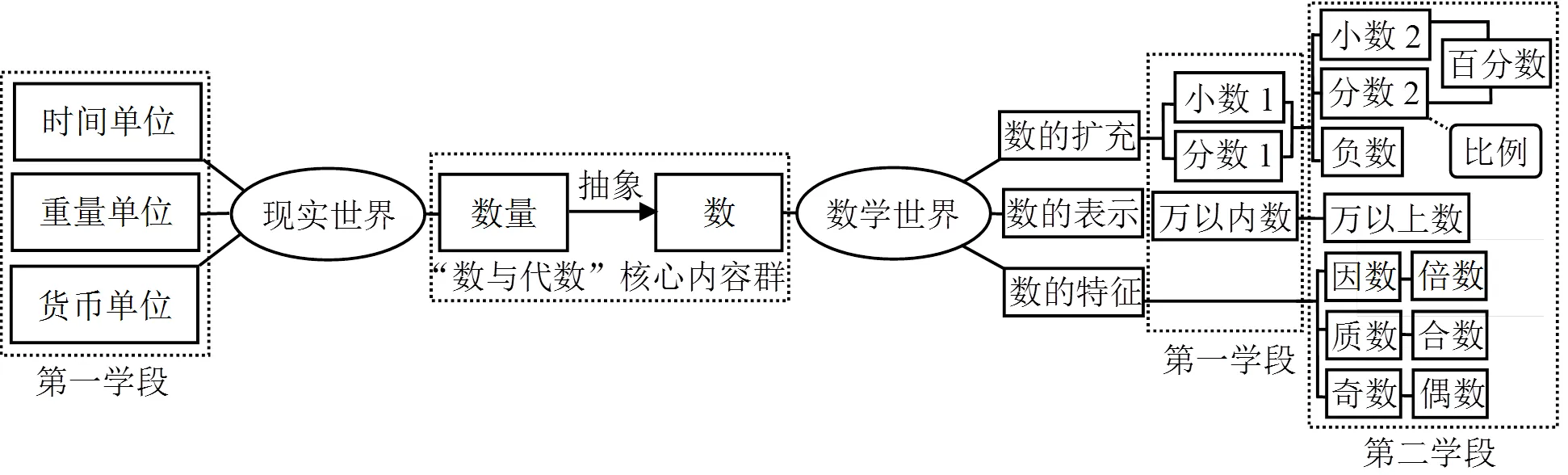
圖1 核心內容群：數與數量網絡圖

小學階段“數與數量”的內容也是由現實世界的數量到數學世界數的抽象，可以從三個角度來理解：第一，數位與計數法；第二，數域的擴充；第三，數的特征分類。如圖1所示，小學數學第一學段和第二學段分別接觸萬以內的數和萬以上的數，自然數表示實現由小到大的關鍵在于數位與計數法的使用。數位是指在一個數中每個數字符號所占的位置，一個數字符號不僅代表自身的數值，還隱含著它所在的數位，即使是同一個數字符號，由于所在數位不同，計數單位不同，所表達的含義也就不同。在眾多計數法中，我國的十進位制（滿十進一，四位一級）記數體系成為普遍采用的方法。馬克思認為：“中國的十進位制是最美妙的發明之一。”[7]也正是因為數位與十進制，我們才能夠利用“0～9”十個數字符號表示出所有的自然數。在我國，除了利用數位記數法來表示自然數，還有一種科學記數法。在科學記數法中，如果采用十進制記數，那么我們稱“10”為基底，一般來說，是幾進制，基底就是幾。有了基底，任意一個自然數都可以表示成基底的線性組合的形式，例如

9 527(10)=9×103+5×102+2×101+7×100”。兩種記數法雖然表現形式不同，但在本質上是一致的，基底的冪是數位與進位制的合二為一。

數域擴充的根本原因在于運算，當一個數域對某種運算不再保持封閉性時，便會有新的數產生，從而再次保證運算的封閉性，實現數域的擴充。在小學階段涉及兩次數的擴充，第一次是在小學第一學段——分數的出現，這是因為自然數對于除法運算不再保持封閉，例如“2÷3”的結果不是自然數，從而需要引入分數；第二次是在小學第二學段——負數的出現，這是因為正整數對減法運算不再保持封閉，例如“2-3”的結果不是正整數，從而需要引入負數。分數的現實意義有兩個，第一個意義是整體與等分，通過等分形成分數單位，這是非常重要的概念，無論是在分數的運算，還是分數的大小比較，都是以分數單位作為基礎；第二個意義是整數的比例關系，體現了除法運算結果，這里需要注意的是分數是除法運算的結果（數），而不是除法運算本身[6,p13-15]。小數作為分數另外一種表示形式，它的出現比微積分還要晚100多年。如上所述，我們利用科學記數法可以得到

9 527=9×103+5×102+2×101+7×100”，

而對于9.527依然可以寫成基底10的線性組合形式，即

9.527=9×101+5×10-1+2×10-2+7×10-3”，

與整數不同的是，這里用10的負整數冪表示，所以小數使分數與整數在表征形式上得到了統一。除此以外，小數另一個重要的價值在于對無理數和有理數的描述。所謂無理數是指無限不循環小數，而有理數是指有限小數和無限循環小數。負數的引入并非一帆風順，起初人們在解方程時以否認回避的態度對待負根。古希臘數學家丟番圖（Diophantus）曾將負數解視為“荒唐的東西”加以舍棄；我國唐代數學家王孝通的《緝古算經》對負根也只字不提；然而，負數作為正數的補充，來源于社會實踐，并在實踐的推動之下逐漸被世人公認。

我們根據自然數特征，按照不同的標準將其分類。以能否被2整除為標準分為奇數和偶數，所有的奇數用2+1（∈Z）表示，所有的偶數用2（∈Z），這對后期數列的學習有著重要作用；以因數是否只有1和自身為標準分為質數（素數）和合數。素數是數論的主要研究對象，在數論中，與素數相關的定理很多，例如歐拉函數、高斯的二次互反律、歌德巴赫猜想等等，素數為數論的發展提供了素材；而對于因數和倍數，在小學階段，公因數為分數約分奠定基礎，公倍數為分數通分奠定基礎。

2.1.2 運算

運算在小學數學中開始最早，時間跨度最長，運算內容采用螺旋式組織方式，如圖2所示。從數學發展的邏輯體系來看，加法運算是四則運算的基礎，可以將減法運算視為加法運算的逆運算，將乘法運算視為特殊的加法運算，而將除法運算視為乘法運算的逆運算。運算包含兩個層面：第一，是對數字符號（常量）的四則運算；第二，是對字母符號（變量）的四則運算。在數學發展史上，數字運算施行于具體的數，而字母運算施行于事物的形式[5,p129]。從數字進行具體的演算到利用符號進行抽象的形式演算，人類經歷了漫長的歲月，但無論是數字運算，還是字母運算，其本質在于算理的把握，例如在加法運算中，加一個正數所得結果一定比原來的數大。

圖2 核心內容群：運算網絡圖

小學階段的估算不需要精確計算來解決問題，其本質在于獲得一定誤差允許范圍內運算結果的上界或下界，是心算、數感、算術技巧之間相互作用的過程。小學的兩個學段都涉及到估算，但是側重點有所不同：第一學段的估算主要側重在實際情境中合理估算測量單位，例如，估計書本長度時一般采用厘米作為單位；第二學段的估算主要側重利用合理的估算解決問題，例如9.9×5.9與50的大小關系。

2.1.3 式與方程

由“數”到“式”是學生對數的符號化表征進一步抽象的過程，“式”不是確定性的數，是可以取得不同數值的符號，而字母表示數的出現，意味著代數學的開始，第一個有意識地使用字母進行抽象運算的是法國數學家韋達[6,p32-33]。對韋達字母符號的改善工作由笛卡爾完成，他首先用拉丁文字母的前幾個（，，，，……）表示已知量，后幾個（，，，，……）表示未知量，形成今天的習慣[5,p129]。從理論上講，代數是字母的算術，代數思維的本質是關系思維，其目的是發現具有一般化的關系、普遍化的結構[8]，例如用符號表示運算律、計算公式，都是將數的知識提升到一般化的水平。自此數學開始進入變量數學的時代，從常量到變量的過渡，是數到符號的轉變，是具體思維到抽象思維的飛躍。變量是從數量關系上反映客觀事物的運動和變化，變量的出現為方程、函數等重要概念登上數學的舞臺奠定了重要的基礎，對數學發展的影響是巨大的。

方程是從現實世界到數學世界的一個提煉過程，實現了數學從數量關系到等量關系的轉變，其本質在于利用數學的符號表達等價關系，方程思想集中體現在建模與化歸兩個方面[9]。因此方程的結構包含了等量關系、代數式的運算結構以及等式變形的結構，這里所說的結構是指“從語言表達抽象出來的一種形式”[10]。而小學第二學段出現的簡易方程作為刻畫現實情境中等量關系的工具，其價值在于提供用代數方法解決現實問題的途徑，而代數方法的出發點就是建立模型，進而促使學生形成從現實世界抽象到數學符號的建模過程，為以后方程與方程組的學習奠定基礎。方程建模說明了數學與現實生活密不可分的關系，而方程的求解是利用四則運算的算術思路來計算未知數。

2.2 小學數學“圖形與幾何”領域核心內容群

《課程標準（2011年版）》指出：“空間觀念主要是指根據物體特征抽象出幾何圖形，根據幾何圖形想象出所描述的實際物體；想象出物體的方位和相互之間的位置關系；描述圖形的運動和變化；依據語言描述畫出的圖形等。”[3,p6]基于此我們將小學數學“圖形與幾何”的核心內容群定為圖形的空間描述和圖形的度量。

2.2.1 圖形的空間描述

圖形的空間描述是以空間視覺為基礎，形成空間物體在形狀、變換、位置關系等特征的屬性表象[11]，包括圖形的認識、圖形的運動、圖形的位置三部分，位于小學數學的第一學段和第二學段，如圖3所示。圖形的認識依賴于人們對現實世界中物體外部輪廓特征的抽象，從而實現三維空間的物體到二維平面圖形的轉化[12]。圖形的運動和圖形的位置是圖形量化研究的兩個重要領域，其關鍵在于參照系，因此它們實現的前提是笛卡爾與費馬將數與圖形的有機結合，創立坐標系和解析幾何學[12,p119]。

圖3 核心內容群：圖形的空間描述網絡圖

在小學階段，兒童對圖形的認識基于日常生活中積累的關于圖形的生活經驗，通過觀察、想象認識常見的立體圖形與平面圖形。而認識圖形的關鍵在于圖形的分類，在分類時不僅要關注圖形之間的共性，還要關注圖形之間的差異，例如長方體與圓柱雖然都屬于空間幾何體（共性），但是長方體是多面體而圓柱是旋轉體（差異）。分類的關鍵在于制定標準，遵循某一標準進行分類的過程也是培養學生抽象能力的過程[13]。

圖形的位置出現在兩個學段，第一學段，描述物體所在方向，其本質是方位角的滲透。在第二學段，主要包含兩部分內容：（1）利用數對描述方格紙上點的位置，其本質是直角坐標系下的數對與點的一一對應關系；（2）利用方向和距離確定事物的位置，其本質是極坐標下的數對與點的一一對應關系。小學階段關于圖形運動的基本形式有兩種：一是圖形的形狀和大小不變，位置發生變化的剛體運動，例如圖形的平移變換、旋轉變換、反射變換；二是圖形的形狀不變，大小發生變化的相似運動，例如放縮變換。我們可以利用圖形的運動來描述一些圖形的相關概念，例如利用平移變換描述平行線，即通過平移得到的直線與原直線平行；利用旋轉變換描述圖形的中心對稱；利用反射變換描述軸對稱以及利用放縮變換描述圖形的相似。

2.2.2 圖形的度量

小學階段圖形的度量可以分為平面圖形的度量和立體圖形的度量，如圖4所示。

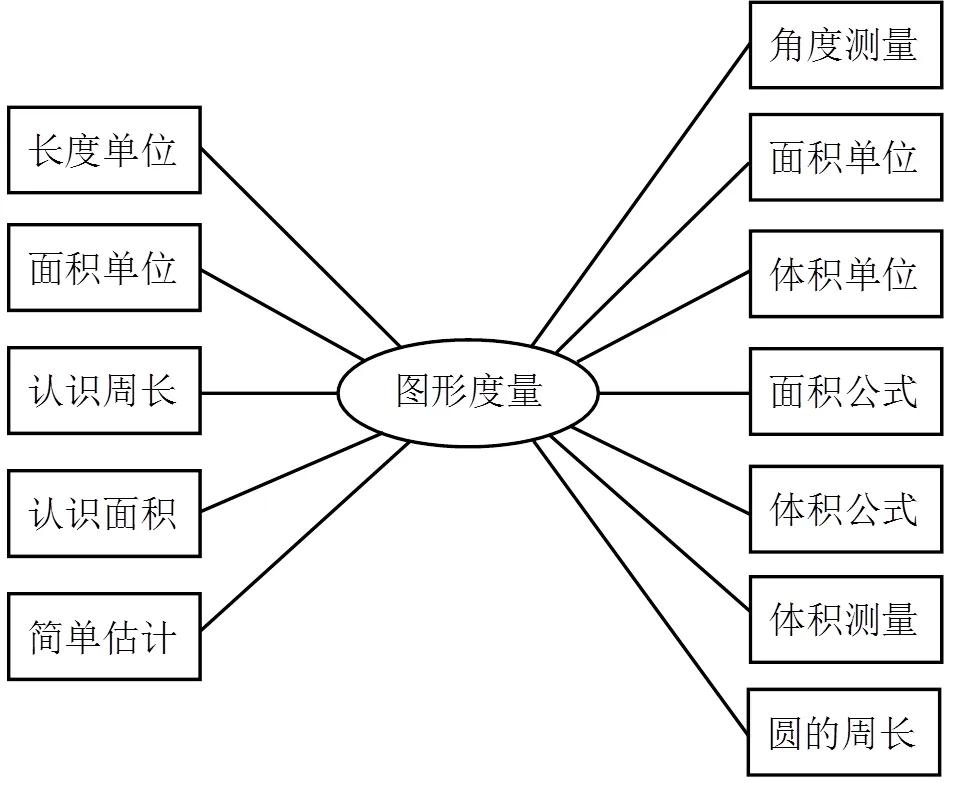
圖4 核心內容群：圖形度量網絡圖

平面圖形可以從長度（一維）、面積（二維）兩個角度來度量，而立體圖形可以從體積（三維）角度來度量。度量的本質就是圖形所包含的度量單位的多少，因此度量的條件是度量單位，度量的要求是單位的統一，所以在小學數學的第一學段涉及了國際通用長度單位、面積單位的認識，第二學段涉及體積單位的認識，為圖形的度量提供基礎條件。除此之外，第一、二學段都涉及了估測，第一學段要求“估測一些物體的長度、給定的簡單圖形的面積”，第二學段要求“體驗某些實物體積的測量”，例如測量一個土豆的體積，可以轉化為測量與土豆等體積的規則物體的體積測量，有利于培養學生轉化與化規思想[14]。

2.3 小學數學“統計與概率”領域核心內容群

如果說描述確定性現象的數學培養學生的確定性思維，那么概率與統計就是通過找出客觀事物的統計規律性和隨機現象中的客觀規律性，來培養學生的因果推斷思想和隨機思想。有助于學生形成偶然中蘊涵著必然以及變與不變的辯證思維[15]，因此我們將小學數學“統計與概率”領域的核心內容群定為數據統計與隨機現象。

2.3.1 數據分析

統計學的基礎是數據，主要研究如何合理收集、整理、分析數據，為人們制定決策提供理論依據。可從三個層面理解數據分析。第一，對數據中蘊含信息的提取。我們所收集到的數據可能是雜亂無章的，并不能直接從中看出統計規律，所以需要對數據進行整理，提取有用的數據信息，因此數據信息的提取是數據分析前提。第二，對數據分析方法的選擇。在小學階段主要有條形統計圖、扇形統計圖、折線統計圖等數據分析方法，不同的分析方法對應不同的問題，因此需要根據待解決問題選擇合適的分析方法。如果希望得到數據中某些數量之間的差異，可以選擇條形統計圖；如果希望了解不同部分所占總體的百分比，可以選擇扇形統計圖；如果希望得到數據變化趨勢，可以選擇折線統計圖。分析方法的選擇是數據分析的保障。第三，對分析結果的預測。數據分析結果具有一定的隨機性，其原因在于每次所選擇數據的不同。因此在小學階段，只能根據分析結果做出簡單的判斷和預測，使學生初步體會統計中因果推斷的思想，分析結果的預測是數據分析的目的[16]。

2.3.2 隨機現象

隨機現象發生的可能性大小用概率來表示，雖然概率是未知的，但是隨機現象具有統計規律性，這種統計規律是一種總體規律，一定是在大量同類隨機現象中才能呈現，它的存在構成了或然數學的研究基礎[17]。在小學階段，要求學生感受隨機現象，我們可以從兩個層面理解隨機現象：第一個層面是對隨機現象本身的認識；第二個層面是對隨機現象的合理解釋[18]。列出簡單的隨機現象中所有可能發生的結果（基本事件），體會隨機現象結果發生的可能性大小（概率），對其做定性的描述，這些內容為古典概率模型（古典概型）的學習奠定基礎。小學階段關于概率的學習，重點在于借助現實情境，通過大量的重復試驗，利用頻率來感悟概率。例如拋硬幣正面向上的概率，可以通過總結事件發生的頻率變化趨勢而得出。隨著拋硬幣試驗次數的增多，正面向上的頻率在0.5上下波動（如表1），可以估計硬幣正面向上的概率為0.5，其依據為頻率是概率的估計值，而概率是頻率的穩定值。

表1 拋硬幣正面向上的頻率變化趨勢[19,p216]

3 小學數學核心內容群教學設計分析

在教學設計中，不同學段相同學習領域內所對應的相關數學內容采用螺旋式組織形式，漸次提高所重復學習的主要概念和觀念的深度和復雜程度，使小學數學核心內容群與學生內部心理過程綜合起來，在不同學段對其他小學數學內容提供動態支持，這種支持不僅包括數學概念、定理和公式等人們在長期數學活動中形成的間接經驗，還包括學習者通過自身的觀察、操作、比較、分析、歸納、概括等活動而獲得的直接經驗，下面以“字母表示數”與“分數乘法”的教學設計片段為例進行分析。

3.1 字母表示數中的數量關系

“字母表示數”屬于式與方程，是小學生初步接觸數學抽象的內容，既是對數的學習的總結，也是對式的學習奠基，具有承上啟下的作用。在教學中，教師用《數青蛙》兒歌來引導學生理解用字母表示數[19,p58]：

一只青蛙一張嘴，兩只眼睛四條腿。

兩只青蛙兩張嘴，四只眼睛八條腿。

三只青蛙三張嘴，六只眼睛十二條腿。

……

讓學生邊拍手邊有節奏地數青蛙，與此同時課件出現很多青蛙，直到數不清，這時教師提問：我們可以用今天所講的內容將這首兒歌數完嗎？

學生在練習紙上填寫：

生1：無數只青蛙無數張嘴，無數只眼睛無數條腿。

生2:a只青蛙b張嘴，c只眼睛d條腿。

生3:a只青蛙a張嘴，b只眼睛c條腿。

生4：a只青蛙a張嘴，aa只眼睛aaaa條腿。

生5:只青蛙張嘴，2只眼睛4條腿。

在實際教學中，能夠真正說出第五種答案的學生，其實并不多，大部分表現為第二種、第三種。與成人思維不同，小學生對于字母表示數難以理解，主要原因在于：（1）字母表示數體現了數學的抽象，這個學習過程是學生從具體數字到抽象字母的轉變過程，是從算術思維向代數思維的轉變過程，體現了數學符號意識；（2）在教學中，大部分教師會反復強調“字母可以表示任意數”，這是導致學生出現第二種或第三種答案的主要原因，學生只關注到字母可以表示任意數，沒有明確數量之間的關系。

字母表示數的本質在于描述數量之間的關系，這種關系體現了一般性，當我們用a、b、c、d表示任意數的時候，更應該說明它們之間的關系，符號化有助于數量關系理解，學生利用符號或者圖形來表示量與量之間的關系，讓符號在表達時產生數學意義，這種符號化表達使數量關系具有一般性，在這個過程中，實現了由常量到變量的過渡。學生要學會用符號或者符號組成的比例關系、方程等模型去描述、分析、解決數學問題。還可以運用字母表示以前學過的法則和公式（如加法運算律、乘法運算律、長方形面積公式、圓柱體積公式、路程速度時間的關系），在表示公式和法則的活動中，學生將進一步體會字母的“概括”作用，從而運用字母及其運算可以表示一般的規律。

3.2 分數乘法中的幾何直觀

生：一個是乘以整數，一個是乘以分數

師：今天重點研究分數乘分數（板書），這對于我們來說是一個新的挑戰。對于這樣一個新的問題，我們用什么方法來研究？

生：可以用畫圖的方法？

師：怎么想到的？

生：以前用畫圖方法研究分數的：

圖5 分數乘法圖形表示

4 結語

數學核心內容群是小學生數學核心素養的重要載體，在數學課程中起到主線的作用，貫穿整個數學教學。經過由古至今的漫長發展，現代數學已經是一個分支眾多的知識系統，孤立的數學內容是不存在，小學數學內容作為整個數學知識系統的縮影，是眾多數學內容按照一定的學科邏輯順序和學生認知結構順序而進行的有效組織，小學數學核心內容群或者以本源內容的形式，或者以小學數學內容主線的形式體現。聚焦小學數學核心內容群進行教學設計，能夠實現數學課堂的有效教學。

[1] 中國社會科學院語言研究所詞典編輯室.現代漢語詞典[Z].北京:商務印書館,2010:554.

[2] 陳祥彬.在小學數學教學中滲透數學思想方法[J].課程·教材·教法,2010,(7):37-41.

[3] 中華人民共和國教育部.義務教育數學課程標準(2011年版)[M].北京:北京師范大學出版社,2011:5.

[4] 卡爾·B.博耶.秦傳安,譯.數學史[M].北京:中央編譯出版社,1991:3-4.

[5] 李文林.數學史概論[M].北京:高等教育出版社,2000: 11.

[6] 史寧中.數學思想概論——數量與數量關系的抽象[M].長春:東北師范大學出版社,2008:5-8.

[7] 徐品方,張紅.數學符號史[M].北京:科學出版社,2007: 22.

[8] 徐文彬,楊玉東.“本源性問題”及其在數學課堂教學中的應用[J].數學教育學報,2005,(3):14-16.

[9] 史寧中,孔凡哲.方程思想及其課程教學設計——數學教育熱點問題系列訪談錄之一[J].課程·教材·教法, 2004,(9):27-31.

[10] 史炳星.從算術到代數[J].數學教育學報,2004,(2):79- 81.

[11] 韓龍淑,呂傳漢.空間觀念的含義和特征及其教學策略[J].數學教育學報,2010,(6):20-22.

[12] 史寧中.數學思想概論——圖形與圖形關系的抽象[M].長春:東北師范大學出版社,2009:2.

[13] 史寧中.基本概念與運算法則——小學數學教學中的核心問題[M].北京:高等教育出版,2013:57.

[14] 史寧中,等.義務教育數學課程標準(2011年版)解讀[M].北京:北京師范大學出版社,2012:57.

[15] 曹學良,鄭潔.關于概念圖在概率統計教學中應用的一些思考[J].數學教育學報,2007,16(1):37-39.

[16] 童莉,張號,張寧.義務教育階段學生數據分析觀念的評價框架建構[J].數學教育學報,2014,23(2):45- 48.

[17] 朱家生,姚林.數學,它的起源與方法[M].南京:東南大學出版社,1999:162-163.

[18] 章飛.義務教育階段概率有關知識的內容定位與教材實施[J].數學教育學報,2004,(1):48-51.

[19] 馬云鵬.小學數學課程標準與教材研究[M].北京:高等教育出版社,2016.

The Core Content Cluster of Elementary School Mathematics: Essence Analysis and Teaching Design

WU Li-sha

(Department of Mathematics and Information Sciences, Tangshan Normal University, Tangshan 063000, China)

The core content cluster of elementary school mathematics can connect different learning section of primary school mathematics in three areas of study including number and algebra, graphics and geometry, statistics and probability. And it provides persistent and fundamental mathematical knowledge structure and mathematical thinking method. The feature of core content cluster is associativity, persistence, foundation and ideology. From the perspective of the development and the essence of mathematics, the core content cluster is beneficial to the design of teaching strategy and the development of teaching resources in elementary school mathematics.

core cluster of elementary school mathematics; essential analysis; teaching design

G622.3

A

1009-9115(2019)03-0130-07

10.3969/j.issn.1009-9115.2019.03.032

河北省高等學校人文社會科學研究項目（SZ18058），河北省教育廳人文社會科學重點項目（SD182012）

2019-01-20

2019-02-22

武麗莎（1986-），女，河北唐山人，碩士，助教，研究方向為數學課程與教學論。

（責任編輯、校對：高俊霞）