被動(dòng)信號(hào)優(yōu)先策略下現(xiàn)代有軌電車站間協(xié)調(diào)能耗優(yōu)化*
歐冬秀 閆 黃 陽 揚(yáng)
(1.同濟(jì)大學(xué)道路與交通工程教育部重點(diǎn)實(shí)驗(yàn)室,201804,上海;2.同濟(jì)大學(xué)經(jīng)濟(jì)與管理學(xué)院,200092,上海;3.上海市軌道交通結(jié)構(gòu)耐久與系統(tǒng)安全重點(diǎn)實(shí)驗(yàn)室,201804,上海;4.卡斯柯信號(hào)有限公司,200071,上海∥第一作者,教授)
現(xiàn)代有軌電車運(yùn)行環(huán)境為城市道路,易受到交叉口信號(hào)控制和社會(huì)車流等因素影響,使得現(xiàn)代有軌電車站間運(yùn)行不連續(xù),運(yùn)行效率得不到有效保障。因此,建立適用于現(xiàn)代有軌電車系統(tǒng)的運(yùn)行能耗優(yōu)化模型具有重要意義。
完全獨(dú)立路權(quán)下現(xiàn)代有軌電車能耗優(yōu)化模型,與鐵路和地鐵相類似。這方面的已有研究對(duì)駕駛策略的探討較多。隨著研究問題的深入和智能控制理論的發(fā)展,國(guó)內(nèi)外學(xué)者還相繼將遺傳算法、蟻群算法和動(dòng)態(tài)規(guī)劃等理論應(yīng)用在模型求解中,取得了大量成果[1-8]。然而,對(duì)于半獨(dú)立路權(quán)的現(xiàn)代有軌電車線路,由于列車運(yùn)行受交叉口信號(hào)控制,到達(dá)路口時(shí)的信號(hào)狀態(tài)將會(huì)影響列車站間運(yùn)行的連續(xù)性。現(xiàn)代有軌電車交叉口信號(hào)優(yōu)先控制策略主要包括被動(dòng)優(yōu)先、主動(dòng)優(yōu)先及實(shí)時(shí)優(yōu)先。被動(dòng)信號(hào)優(yōu)先采用固定信號(hào)配時(shí),通過協(xié)調(diào)干線上各交叉口的信號(hào)方案實(shí)現(xiàn)干線協(xié)調(diào)控制,為現(xiàn)代有軌電車列車提供信號(hào)優(yōu)先[9-10]。因此,在建立半獨(dú)立路權(quán)現(xiàn)代有軌電車運(yùn)行節(jié)能優(yōu)化模型時(shí),需要考慮被動(dòng)信號(hào)優(yōu)先策略的影響。
目前,對(duì)于現(xiàn)代有軌電車能耗的研究多集中于車輛性能和電容控制上。文獻(xiàn)[11]通過設(shè)定不同車輛加速時(shí)間和最大運(yùn)行速度來對(duì)比車輛能耗,尋找最優(yōu)駕駛行為;文獻(xiàn)[12]通過設(shè)定車輛性能、線路條件和運(yùn)營(yíng)組織模式等多個(gè)參數(shù)來對(duì)比能耗,從而提出節(jié)能優(yōu)化措施;文獻(xiàn)[13-14]通過仿真路口是否停車、路口區(qū)域是否限速等因素對(duì)列車能耗進(jìn)行對(duì)比研究,提出節(jié)能方案。上述研究始終未將交叉口信號(hào)控制因素引入現(xiàn)代有軌電車能耗模型中,因此無法指導(dǎo)半獨(dú)立路權(quán)有軌電車線路的節(jié)能優(yōu)化。
本文依據(jù)半獨(dú)立路權(quán)現(xiàn)代有軌電車線路特征進(jìn)行區(qū)段劃分,通過分析現(xiàn)代有軌電車列車運(yùn)行模式,推算單區(qū)段現(xiàn)代有軌電車能耗優(yōu)化速度曲線;進(jìn)而研究站間協(xié)調(diào)的現(xiàn)代有軌電車全線能耗優(yōu)化模型;最后,通過遺傳算法對(duì)該模型進(jìn)行求解并進(jìn)行節(jié)能結(jié)果對(duì)比分析。
1 單區(qū)段能耗優(yōu)化速度曲線
1.1 區(qū)段劃分
鐵路與地鐵線路兩個(gè)車站之間的區(qū)間,稱為站間區(qū)間,簡(jiǎn)稱為站間。站間中存在多個(gè)限速值變化點(diǎn),據(jù)此可以將站間劃分為多個(gè)限速保持一致的區(qū)段,這是建立能耗優(yōu)化模型的基礎(chǔ)。
半獨(dú)立路權(quán)現(xiàn)代有軌電車除在站點(diǎn)停車外,還存在交叉口的影響。在被動(dòng)信號(hào)優(yōu)先策略下,列車在交叉口遇紅燈需停車,遇綠燈需限速通過,這是現(xiàn)代有軌電車與鐵路和地鐵最主要的區(qū)別。因此,在對(duì)現(xiàn)代有軌電車線路進(jìn)行區(qū)段劃分時(shí),需要將交叉口作為可變因素進(jìn)行考慮。
現(xiàn)代有軌電車站間區(qū)間內(nèi)除交叉口外,還存在影響速度曲線變化的環(huán)境分界點(diǎn),如坡道、彎道和隧道的起始點(diǎn)。同時(shí),在交叉口區(qū)域內(nèi)列車限速值也會(huì)改變,所以交叉口的停車線位置和出口位置同樣是區(qū)段分界點(diǎn)。為此,站間區(qū)間的速度曲線將根據(jù)環(huán)境分界點(diǎn)與交叉口區(qū)段端點(diǎn)兩種要素進(jìn)行劃分,列車在這些位置存在限速,這會(huì)導(dǎo)致速度曲線產(chǎn)生相應(yīng)變化。
此外,對(duì)于布設(shè)在交叉口附近的現(xiàn)代有軌電車站點(diǎn),由于站點(diǎn)距交叉口進(jìn)口或出口較近,在區(qū)段劃分上將交叉口與車站兩點(diǎn)重新定義,即站點(diǎn)與交叉口的遠(yuǎn)端點(diǎn)構(gòu)成一個(gè)區(qū)段。列車在此區(qū)段內(nèi)一定會(huì)產(chǎn)生停車,停車等待時(shí)間為駐站時(shí)間加上信號(hào)等待時(shí)間。區(qū)段劃分示意圖如圖1所示。
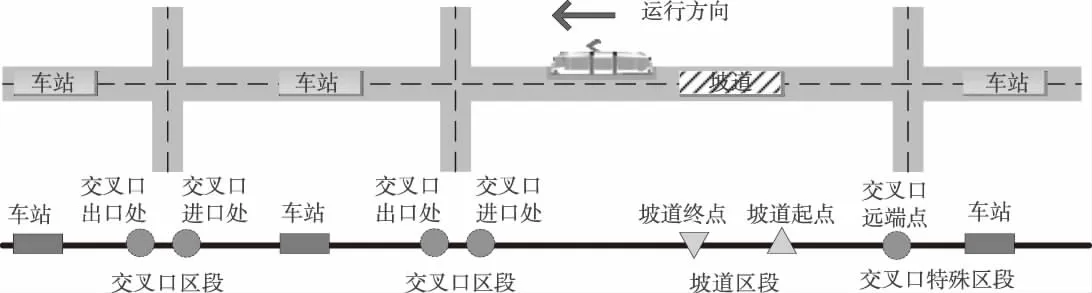
圖1 現(xiàn)代有軌電車站間區(qū)段劃分線路平面與拓?fù)鋵?duì)比示意圖
1.2 速度曲線推導(dǎo)
站間區(qū)間內(nèi)含有多個(gè)區(qū)段,列車在單個(gè)區(qū)段中的運(yùn)行環(huán)境相對(duì)較為穩(wěn)定。假設(shè)在一個(gè)區(qū)段內(nèi),列車存在牽引、巡航、惰性和制動(dòng)4種運(yùn)行模式,每種模式只會(huì)在一定的連續(xù)時(shí)間內(nèi)采用1次,因此有:

式中:
Ssec(i)、Strac(i)、Scr(i)、Sco(i)、Sb(i)——分別表示區(qū)段內(nèi)的軌道長(zhǎng)度、牽引距離、巡航距離、惰行距離、制動(dòng)距離;
βtrac(i)、βcr(i)、βco(i)、βb(i)——分別為相對(duì)應(yīng)各項(xiàng)的系數(shù),該系數(shù)取值由各區(qū)段內(nèi)列車的運(yùn)行模式所決定,取值為0或1。
以區(qū)段入口速度與出口速度(即分界點(diǎn)速度)為依據(jù),可將列車在區(qū)段內(nèi)的運(yùn)行分為以下4種情況:
(1)入口速度與出口速度都低于交叉口限速或?yàn)?;
(2)入口速度小于出口速度,入口速度低于交叉口限速或?yàn)?,出口速度高于交叉口限速或?yàn)?;
(3)入口速度大于出口速度,入口速度高于交叉口限速,出口速度低于交叉口限速或?yàn)?;
(4)入口速度與出口速度都高于交叉口限速。
對(duì)于上述4種情況,在確定的區(qū)段長(zhǎng)度和限速下可以得到此區(qū)段滿足式(1)的速度曲線解集。通過設(shè)置運(yùn)行時(shí)間約束,比較能耗變化可推導(dǎo)出最優(yōu)速度曲線。推導(dǎo)流程如圖2所示。
為了便于計(jì)算,推導(dǎo)過程中速度分辨率設(shè)定為1 km/h。實(shí)際中的列車在站間區(qū)間運(yùn)行時(shí)間需要滿足正點(diǎn)運(yùn)行需求,而通過區(qū)段劃分,運(yùn)行時(shí)間約束分散到各個(gè)單區(qū)段上。設(shè)置單區(qū)段運(yùn)行時(shí)間約束,一方面要求計(jì)算所得運(yùn)行時(shí)間與設(shè)定運(yùn)行時(shí)間的差值逐漸降低,另一方面該差值在一定范圍(設(shè)定閾值)內(nèi)變化即認(rèn)為有效。
2 站間協(xié)調(diào)控制列車能耗優(yōu)化模型
包含交叉口的區(qū)段中,出入口限速?zèng)Q定于列車到達(dá)交叉口時(shí)的信號(hào)燈狀態(tài)。在沿線交叉口為固定配時(shí)策略下,通過線路參數(shù)、列車發(fā)車時(shí)刻、交叉口信號(hào)參數(shù)等得到列車沿線交叉口通行情況計(jì)算規(guī)程,主要計(jì)算當(dāng)列車在某一時(shí)段抵達(dá)某交叉口時(shí)信號(hào)燈狀態(tài)。列車能耗隨著區(qū)段運(yùn)行時(shí)間的增長(zhǎng)而降低,據(jù)此可調(diào)整各區(qū)段運(yùn)行時(shí)間。將列車在交叉口等待信號(hào)時(shí)間分配到各區(qū)段中,降低區(qū)段運(yùn)行最大速度,調(diào)整速度曲線;按照同一區(qū)間中區(qū)段能耗減少量大小分配時(shí)間,在滿足站間運(yùn)行時(shí)間約束下盡可能降低運(yùn)行能耗。
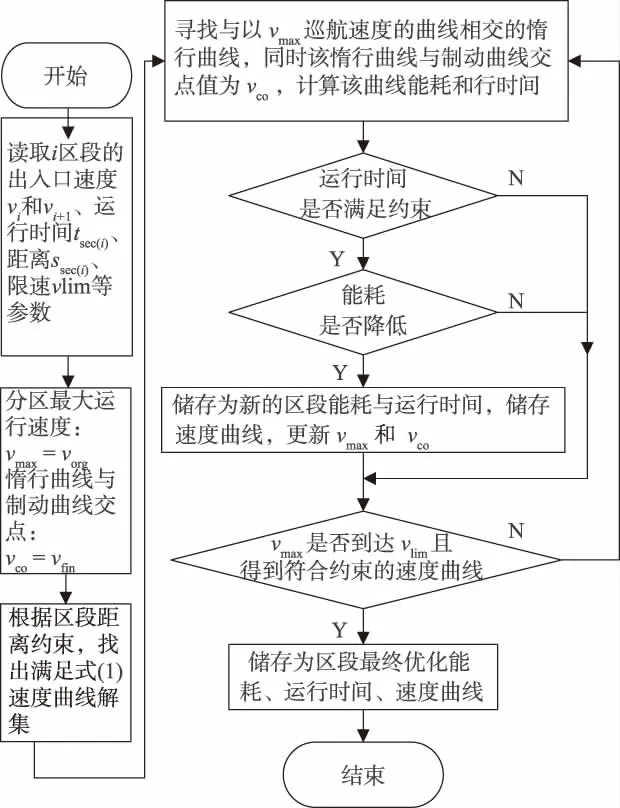
圖2 單區(qū)段能耗優(yōu)化速度曲線推導(dǎo)流程
2.1 模型假設(shè)
(1)本文研究對(duì)象為半獨(dú)立路權(quán)現(xiàn)代有軌電車,沿線交叉口信號(hào)已經(jīng)考慮社會(huì)交通流影響,實(shí)施了面向現(xiàn)代有軌電車的被動(dòng)信號(hào)優(yōu)先機(jī)制,優(yōu)化了信號(hào)周期與綠信比。
(2)為滿足列車在車站的充電需求,列車駐站時(shí)間固定,且不低于某一固定值(如30 s),不因上下車客流量變化而發(fā)生改變。
(3)列車運(yùn)行中,牽引時(shí)的牽引力隨牽引曲線變化;制動(dòng)時(shí)保持減速度恒定;巡航時(shí)受力平衡,保持理想勻速狀態(tài);在惰行時(shí)受各項(xiàng)運(yùn)行阻力的影響,減速度隨受力變化。
2.2 模型變量
2.2.1 區(qū)段分界點(diǎn)的瞬時(shí)速度
在現(xiàn)代有軌電車站間能耗優(yōu)化中,各區(qū)段的出入口速度(vi,vi+1)是非常重要的控制因素。本文定義各區(qū)段的出入口速度矩陣為Vtram,則有:
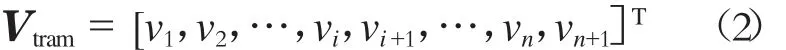
Vtram是包含了現(xiàn)代有軌電車線路上所有區(qū)段出入口速度的集合。各分界點(diǎn)速度vi的取值范圍視分界點(diǎn)的最高限速而定。n為線路上區(qū)段個(gè)數(shù)。
2.2.2 站間運(yùn)行時(shí)間
現(xiàn)代有軌電車運(yùn)行時(shí)需要確定時(shí)刻表,即需要確定站間運(yùn)行時(shí)間,并給出一定的準(zhǔn)許誤差Δt。各站間運(yùn)行時(shí)間為tr-sec(i)。本文定義各站間的運(yùn)行時(shí)間矩陣為 Tr-sec,則有
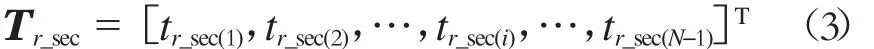
式中,N為現(xiàn)代有軌電車線路上的站點(diǎn)數(shù),即N-1為相應(yīng)的站間區(qū)間數(shù),且N≤n。當(dāng)N=n時(shí),表示線路上沒有任何道路交叉口與環(huán)境分界點(diǎn),列車全線在平直線上運(yùn)行。n-N既是線路上平面交叉口數(shù)量與未合并的環(huán)境分界點(diǎn)數(shù)量之和。
各站間的運(yùn)行時(shí)間取值范圍根據(jù)現(xiàn)代有軌電車列車時(shí)刻表與準(zhǔn)許誤差來確定。
2.2.3 區(qū)段運(yùn)行時(shí)間
當(dāng)站間運(yùn)行時(shí)間確定后,該時(shí)間將作為該站間范圍內(nèi)所有區(qū)段運(yùn)行時(shí)間和的約束。各區(qū)段運(yùn)行時(shí)間tr-sec(i)是直接影響列車運(yùn)行速度曲線的變量之一,其矩陣Tsec表示形式如下:
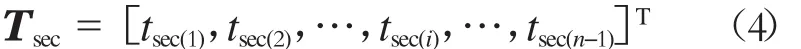
Tsec所有元素求和得到的值應(yīng)與Tr-sec所有元素求和得到的值一致。
2.2.4 發(fā)車時(shí)刻
發(fā)車時(shí)刻決定了列車發(fā)車時(shí)距第一個(gè)交叉口綠燈相位的時(shí)間,將在一定程度上影響列車在第一個(gè)交叉口乃至后續(xù)交叉口的通行情況,是需要調(diào)整與控制的變量之一。
在本文的基本假設(shè)中,現(xiàn)代有軌電車沿線交叉口信號(hào)周期保持一致,且周期的長(zhǎng)度不會(huì)改變。因此,列車以第一個(gè)交叉口信號(hào)周期的每次起始時(shí)刻為0時(shí)刻,列車在每個(gè)周期內(nèi)的第x時(shí)刻發(fā)車,且滿足:

式中:
Tsignal——沿線交叉口信號(hào)配時(shí)的周期長(zhǎng)度。
若速度曲線完全一致,理想情況下,時(shí)刻x下發(fā)出的所有列車在沿線交叉口的通行情況應(yīng)一致。
2.3 優(yōu)化目標(biāo)
本文研究現(xiàn)代有軌電車列車運(yùn)行能耗時(shí),采用的推算方式為列車動(dòng)能變化與阻力做功。根據(jù)列車基本運(yùn)行模式特點(diǎn),列車在牽引、巡航模式下會(huì)產(chǎn)生牽引力,牽引力做功,惰行時(shí)牽引力不做功。其優(yōu)化目標(biāo)為列車所有區(qū)段能耗之和最小,即其中Ei為單區(qū)段能耗值。
2.4 模型約束
為確保求解出合理的速度曲線,需要根據(jù)實(shí)際情況設(shè)置以下模型約束條件,以降低模型求解時(shí)的復(fù)雜度。
(1)各區(qū)段長(zhǎng)度約束。當(dāng)推算各區(qū)段的速度曲線時(shí),需要確保推算出的速度曲線在區(qū)段所經(jīng)過的距離與區(qū)段長(zhǎng)度保持一致。
(2)線路總運(yùn)行時(shí)間約束。當(dāng)?shù)玫秸麠l線路的速度曲線時(shí),需要確保推算出的速度曲線在全線運(yùn)行的時(shí)間不超過線路允許的最大運(yùn)行時(shí)間。
(3)各區(qū)段運(yùn)行時(shí)間約束。各區(qū)段出入口速度與最高限速確定后,列車在區(qū)段的運(yùn)行時(shí)間范圍已確定,需設(shè)置檢驗(yàn)區(qū)段的運(yùn)行時(shí)間約束。
(4)各區(qū)段運(yùn)行速度約束。列車在各區(qū)段運(yùn)行時(shí),需要嚴(yán)格遵循當(dāng)前所處路段的限速,不可以高于區(qū)段限速行駛。
(5)各交叉口通行狀況約束。列車在交叉口分界點(diǎn)的速度需滿足當(dāng)前該交叉口的通行情況。可根據(jù)列車抵達(dá)該交叉口前的運(yùn)行時(shí)間來計(jì)算。
2.5 模型求解
基于對(duì)求解問題的模型化處理與復(fù)雜度考慮,本文選擇采用遺傳算法對(duì)本文所描述的問題進(jìn)行求解。具體步驟如下:將線路環(huán)境參數(shù)輸入生成能耗優(yōu)化初始種群;對(duì)初始種群進(jìn)行二進(jìn)制編碼,主要包括發(fā)車時(shí)刻、各區(qū)段入口速度及區(qū)段運(yùn)行時(shí)間。
以列車速度為例,列車在線路上限速若為70 km/h,則采用7位自然二進(jìn)制編碼0000000~1000110表示0~70 km/h的速度范圍;同樣,列車的發(fā)車時(shí)刻處于0~119 s之間,也需要7位二進(jìn)制編碼0000000~1110111表示。
通過編碼后,設(shè)置適應(yīng)度函數(shù)、基因雜交比例和變異比例等參數(shù),利用Matlab遺傳算法工具箱進(jìn)行編程,解碼后得到優(yōu)化結(jié)果。過程不再贅述,通過實(shí)際案例對(duì)模型進(jìn)行驗(yàn)證和分析。
3 節(jié)能效果仿真對(duì)比分析
選取國(guó)內(nèi)某城市實(shí)際現(xiàn)代有軌電車線路為研究對(duì)象,研究范圍為7站6區(qū)間,如圖3所示。通過VISSIM仿真平臺(tái)搭建仿真線路,仿真模擬駕駛運(yùn)行,獲取仿真速度曲線,計(jì)算能耗,并將結(jié)果與能耗優(yōu)化模型求解結(jié)果進(jìn)行對(duì)比驗(yàn)證。現(xiàn)代有軌電車線路基礎(chǔ)參數(shù)設(shè)定見表1。
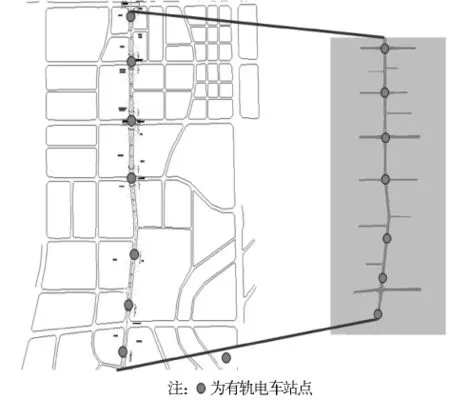
圖3 某城市現(xiàn)代有軌電車部分線路建模圖
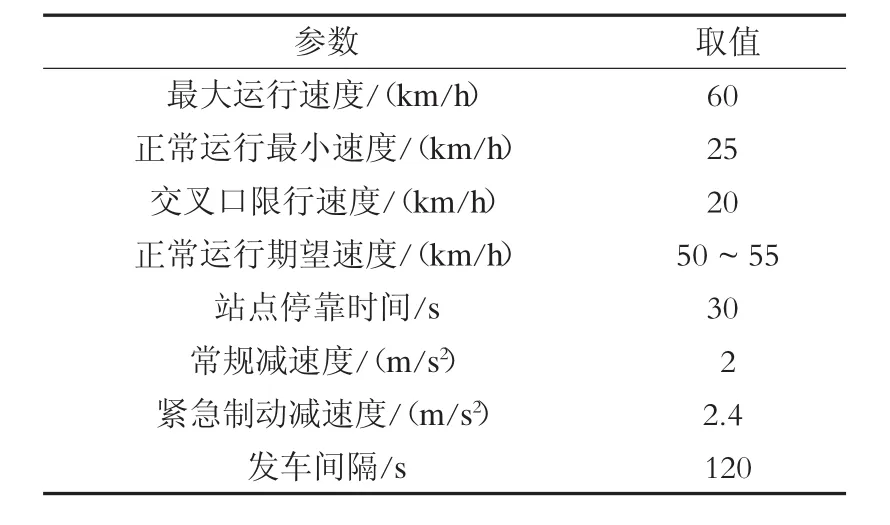
表1 某城市現(xiàn)代有軌電車基礎(chǔ)參數(shù)設(shè)定表
對(duì)于沿線交叉口信號(hào)配時(shí),沿線交叉口信號(hào)周期時(shí)間為120 s,現(xiàn)代有軌電車相位綠燈時(shí)長(zhǎng)30 s。根據(jù)列車常規(guī)運(yùn)行速度,依據(jù)被動(dòng)信號(hào)優(yōu)先綠波帶進(jìn)行相位差計(jì)算和相序組合。
上述參數(shù)作為現(xiàn)代有軌電車對(duì)比仿真驗(yàn)證的基礎(chǔ)參數(shù)。根據(jù)線路參數(shù)生成的模型求解的初始種群,一般采取隨機(jī)生產(chǎn)方式,但可能與實(shí)際情況有較大差異。本文根據(jù)最大運(yùn)行時(shí)間,考慮各區(qū)段長(zhǎng)度與交叉口給出初始種群,發(fā)車時(shí)刻為0 s。設(shè)置基因雜交比例為0.8,變異比例為0.2,每代種群的個(gè)體為100個(gè),共運(yùn)行150代。基礎(chǔ)參數(shù)下仿真速度曲線與模型求解速度曲線對(duì)比如圖4所示。
模型求解結(jié)果為:發(fā)車時(shí)刻為75 s,總運(yùn)行時(shí)間為550 s,列車平均運(yùn)行速度為20.2 km/h,列車運(yùn)行凈能耗為11.46 kW·h,總能耗為13.02 kW·h。而仿真中采取了較為極端的駕駛操作,為盡快抵達(dá)站點(diǎn)或交叉口,仿真中都盡可能采用牽引加速,直至制動(dòng)轉(zhuǎn)換點(diǎn)才制動(dòng)減速,這導(dǎo)致列車在交叉口多次停車等待,浪費(fèi)大量時(shí)間。仿真列車運(yùn)行凈能耗為22.14 kW·h,按88%效率計(jì)算,總能耗為25.15 kW·h。模型求解速度曲線中,列車在交叉口等待時(shí)間被重新協(xié)調(diào)到區(qū)段運(yùn)行時(shí)間約束中,增加了區(qū)段運(yùn)行時(shí)間,降低了區(qū)段平均運(yùn)行速度,且列車在交叉口無需停車,很大程度上節(jié)省了能耗,節(jié)能近48.2%。
沿線交叉口的信號(hào)周期長(zhǎng)度、路段限速、交叉口限速及列車的平均運(yùn)行速度需求,都會(huì)對(duì)能耗優(yōu)化的結(jié)果產(chǎn)生影響。故本文針對(duì)不同的運(yùn)行條件對(duì)能耗優(yōu)化算法的推算結(jié)果進(jìn)行對(duì)比。
(1)路段限速降低至50 km/h。模型求解結(jié)果:發(fā)車時(shí)刻為76 s,能耗優(yōu)化計(jì)算得出的速度曲線凈能耗為11.17 kW·h,總能耗為12.69 kW·h。較限速60 km/h時(shí)能耗優(yōu)化模型求解結(jié)果的能耗下降2.5%。
(2)交叉口限速降低至15 km/h。模型求解結(jié)果:發(fā)車時(shí)刻為82 s,運(yùn)行凈能耗為13.00 kW·h,總能耗為14.77 kW·h,較路段限速60 km/h、交叉口限速20 km/h情況下的能耗增加了11.8%。其原因在于交叉口限速的降低,即列車必須以更低的速度通過交叉口,故列車在駛出交叉口后的牽引能耗增大,而交叉口低速通過浪費(fèi)的時(shí)間必須靠減少在其余分區(qū)的運(yùn)行時(shí)間來彌補(bǔ)。這兩者都會(huì)導(dǎo)致能耗增加。
(3)交叉口信號(hào)周期縮短至90 s。模型求解結(jié)果:發(fā)車時(shí)刻為21 s,運(yùn)行凈能耗降至10.43 kW·h,總能耗為11.85 kW·h,較路段限速60 km/h、交叉口限速20 km/h情況下的能耗降低了9.0%。降低沿線交叉口信號(hào)控制周期,就降低了列車可能停車等待的紅燈窗口,使列車抵達(dá)交叉口時(shí)的通行可能性增大,潛在停車等待時(shí)間減少。
至此,可以發(fā)現(xiàn),路段限速、交叉口限速及信號(hào)周期長(zhǎng)度的調(diào)整都會(huì)對(duì)現(xiàn)代有軌電車的能耗優(yōu)化速度曲線求解造成影響,其影響也基本符合道路交通流的基本特征。
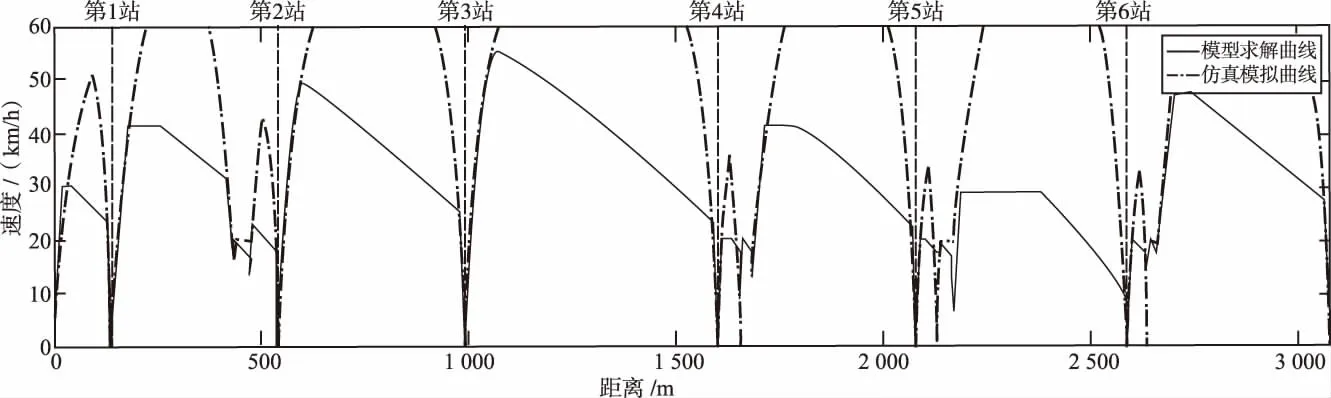
圖4 某城市現(xiàn)代有軌電車仿真速度曲線與模型求解速度曲線對(duì)比圖
4 結(jié)語
本文根據(jù)半獨(dú)立路權(quán)現(xiàn)代有軌電車線路特征,提出了含有交叉口特殊區(qū)段的線路區(qū)段劃分方法。通過分析現(xiàn)代有軌電車運(yùn)行模式的阻力模型及運(yùn)行模式,探討了在單區(qū)段出入口速度、運(yùn)行時(shí)間約束及限速確定的前提下能耗優(yōu)化曲線的求解方法;通過離散運(yùn)行速度,找出滿足約束下的單區(qū)段速度曲線解,并通過逐步迭代的方式求解能耗最優(yōu)的單區(qū)段速度曲線。
本文還搭建了基于站間協(xié)調(diào)的現(xiàn)代有軌電車能耗優(yōu)化模型:在沿線交叉口已經(jīng)考慮被動(dòng)優(yōu)先配時(shí)策略的基礎(chǔ)上,推算信號(hào)燈狀態(tài),將列車在交叉口等待時(shí)間轉(zhuǎn)移到區(qū)段運(yùn)行時(shí)間上;進(jìn)而通過控制各區(qū)段出入口速度、區(qū)段運(yùn)行時(shí)間、路段限速、發(fā)車時(shí)刻等變量,利用遺傳算法對(duì)模型進(jìn)行了求解。結(jié)果顯示,在滿足現(xiàn)代有軌電車運(yùn)行需求的前提下能夠求解得到合理的能耗優(yōu)化曲線。同時(shí)需要指出,本文僅考慮了線路上單列列車的節(jié)能優(yōu)化,而在實(shí)際運(yùn)行中,線路上可能會(huì)有前后車的影響。這是需要進(jìn)一步研究的重點(diǎn)和難點(diǎn)。

