基于碼長近似度的極化碼性能分析
葉銘 李暉 童強 張瑞清
摘 ?要: 極化碼是未來5G通信中的控制信道編碼方案。針對碼長類型不同的極化碼之間的碼長不等性和距離譜性能分析的不確定性等難點問題,提出一種基于碼長近似度的極化碼性能分析方法。該方法能根據碼長近似度直接評估基于2×2核矩陣[G2]和[l×l]多維核矩陣[Gl]的極化碼的性能。實際情況和仿真結果都表明:基于2×2核矩陣[G2]的極化碼比基于3×3核矩陣[G3]的極化碼具有更好的誤比特率和誤幀率性能;碼長近似度越大,所提方法極化碼性能分析的精度越高。
關鍵詞: 極化碼; 碼長近似度; 多維核矩陣; 距離譜; 信道編碼; 誤碼率; 誤幀率
中圖分類號: TN919.3+1?34; TN911.7 ? ? ? ? ? ? ? ?文獻標識碼: A ? ? ? ? ? ? ? ? ?文章編號: 1004?373X(2019)11?0024?04
Abstract: Polar codes coding scheme is a kind of channel?controlling coding scheme for future 5G communication. In allusion to the difficulties of the inequality of code lengths between polar codes with different code length types and uncertainty of distance spectrum performance analysis, a performance analysis method of the polar codes is proposed, which is based on code length approximation degree (CLAD). The performances of polar codes based on 2×2 kernel matrix [G2] and l×l multidimensional kernel matrix [Gl] are evaluated directly according to CLAD. The actual situation and simulation results show that the polar codes based on 2×2 kernel matrix [G2] have higher performances in the aspects of bit error rate (BER) and frame error rate (FER) than polar codes based on 3×3 kernel matrix [G3]. The experimental results demonstrate that the greater the code length approximation degree is, the higher the analysis accuracy of the polar codes performance is.
Keywords: polar code; code length approximation degree; multidimensional kernel matrix; distance spectrum; channel coding; bit error rate; frame error rate
0 ?引 ?言
信道編碼方案中的極化碼是5G通信領域中的研究熱點。最初介紹的極化碼是非系統極化碼(Non?Systematic Polar Codes,NSPCs)[1]。它是一種具有編譯碼復雜度低、可達二進制離散無記憶信道對稱容量的編碼構造方法。這類極化碼的生成矩陣是基于2×2極化核矩陣的。當碼長[N]足夠大,且[β<][12]時,對于任意二進制輸入離散無記憶信道[W]且其對稱容量[I(W)]小于碼率[R],極化編碼在串行抵消(Successive Cancellation,SC)譯碼下的譯碼誤塊率[peN,R=o(2-Nβ)],即[G2]有指數[2][12]。當核矩陣足夠大時,該指數可任意逼近1,且越接近1極化碼的性能越好[3]。因此,研究基于[l×l]核矩陣[Gl]構造的極化碼([l≥3]的核矩陣為多維核矩陣)具有重要意義。
碼長類型為[Nl=ln]的([l≥3])極化碼的合理性已被證明[3],這類極化碼的構造方法也被提出。因此,碼長類型為[N2=2n]形式的限制被打破,極化碼的碼長更加靈活。然而,碼長類型不同的極化碼由于碼長的不等性,給其性能分析帶來很大的困難。與極化核矩陣[G2]只有一種形式所不同的是,多維極化核矩陣在形式方面擁有更多的選擇,在編碼構造上復雜度更大的同時也更加靈活。相應地,基于[l×l]多維核矩陣的極化碼相比基于2×2核矩陣的極化碼更加復雜,前者的編碼構造和碼長類型也不同于后者。
對于多維核矩陣構造的極化碼,本文僅考慮基于3×3核矩陣的極化碼的分析。距離譜可以用來分析極化碼的性能趨勢,但卻不能用來具體地分析多維核矩陣構造的極化碼的性能[2,4]。因為根據距離譜得到的只是極化碼性能的模糊上界。針對這些問題,本文提出一種可以直接分析碼長類型不同的極化碼之間的性能方法。仿真結果表明,碼長近似度越大,該方法極化碼性能分析的精度越高。上述方法對極化碼性能的評估與優化有重要的借鑒意義和理論價值。
1 ?基于3×3核矩陣的極化碼
對于二進制刪除信道(Binary Erasure Channel,BEC),基于3×3多維核矩陣[G3]的極化碼的信道[W(i)N]的可靠性可由下式計算得到[2]:
信道[W(i)N]的可靠性也可通過密度進化或高斯近似的方法計算[5?6]。 基于2×2核矩陣[G2]的極化碼只有一種核矩陣形式,即[G2=1011],而多維核矩陣[Gl]隨著[l]的增大而擁有更多的形式,碼長類型為[Nl=ln]的極化碼在編碼構造上更靈活,同時也更難找出一個更好的核矩陣形式。例如,碼長類型為[N3=3n]的極化碼的核矩陣[G3]就有[24=16]種可能形式,而不同的多維核矩陣形式[G3]滿足信道極化條件的也只有四種[7]。
由不同的多維核矩陣形式構造的極化碼,其性能存在一定的差異。在本文中,不同的多維核矩陣形式[G3]中最好的形式為[G3]427,碼長類型為[N3=3n]的極化碼是基于多維核矩陣[G3]427構造的。
2 ?性能評估方法
這里提出一種新方法以分析基于2×2核矩陣和[l×l]多維核矩陣[Gl]的極化碼之間的性能。
如果要分析碼長類型不同的極化碼,即碼長類型為[Nl=ln]([l≥2,n≥1]),那么應先設定一個碼長閾值[Nf]和碼長近似度閾值[fN],即核矩陣[Gl(l≥2)]構造的極化碼,約定其碼長不能超過[Nf]且碼長近似度[f≥fN]。碼長近似度[f]為碼長類型不同的極化碼中小的碼長數值與較大的碼長數值兩者之間的比值。一般選用碼長數值相近的兩個值求碼長近似度[f],進而求得數值較大的[f]。規定碼長近似度[f≤]1。任意一種碼長類型的極化碼都可以作為一個模板,選其中的一種碼長類型的極化碼作為模板。對于要分析的碼長類型的極化碼與模板,將其碼長數值作比較以求碼長近似度[f],再逐一選擇其中碼長近似度符合要求的碼長數值組。最后,將選擇的碼長數值組視為碼長相等來直接分析并判定碼長類型不同的極化碼之間的性能優劣。
上述方法被稱為基于碼長近似度的極化碼性能評估方法。本方法經過一些處理忽略不同碼長類型的極化碼在碼長數值上的不等性,而直接分析基于核矩陣[G2]和多維核矩陣[Gl]的極化碼的性能,簡單而有效。一般將碼長類型為[N2=2n]的極化碼作為模板,因為其碼長數值較為靈活,碼長數值間的差距最小。
3 ?仿真結果
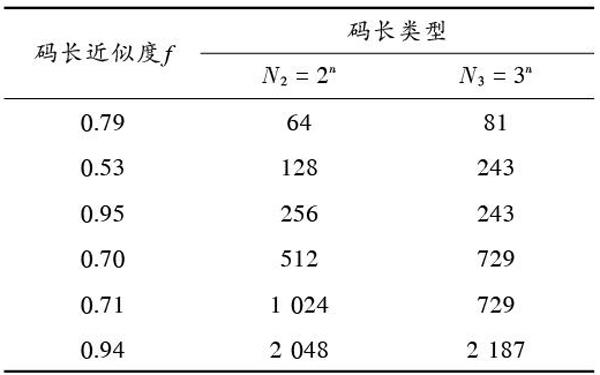
假設要對碼長類型分別為[N2=2n]和[N3=3n]([n≥1])的極化碼進行性能分析和判定。分別設碼長閾值[Nf=]3 000,碼長近似度閾值[f=0.95]。以碼長類型為[N2=2n]的極化碼為模板,則碼長近似度如表1所示。事實上,表1中一些不合理的碼長數值已被去掉。
表1 ?碼長類型分別為[N2=2n]和[N3=3n]的極化碼的碼長近似度

3.1 ?碼長近似度[f=0.95]
從表1中可知,碼長數值分別為256與243的這組碼長數值的碼長近似度符合要求。那么,可將碼長[N2=]256視為與碼長[N3=243]相等,然后直接進行這兩種碼長類型的極化碼的性能分析與判定。這里的仿真實驗是在加性高斯白噪聲信道(Additive White Gaussian Channel,AWGN)下,對碼率為[12]、碼長[N]分別為243和256的極化碼進行的。調制方式為二進制相移鍵控(Binary Phase Shift Keying,BPSK)。串行抵消列表(Successive Cancellation List,SCL)譯碼器的列表大小[8?9]設為32。
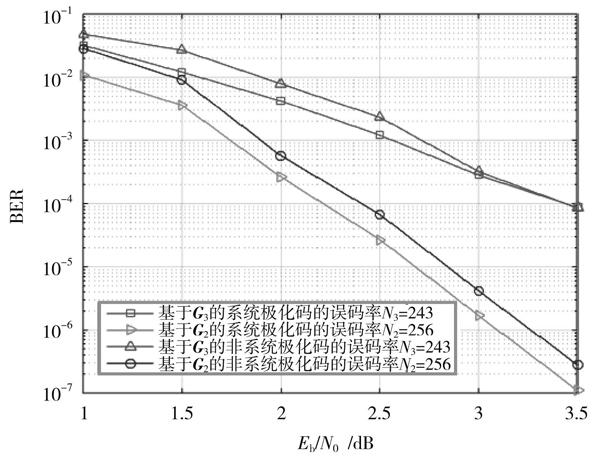
根據上面的方法,這里將碼長[N2=256]和[N3=243]視為等長。碼長[N2=256]和[N3=243]的系統極化碼(Systematic Polar Codes,SPCs)[10]和非系統極化碼的誤碼率的仿真結果如圖1所示。
圖1 ?碼長[N2=]256和[N3=]243的系統極化碼和非系統極化碼的誤碼率

仿真結果表明:基于2×2核矩陣[G2]的非系統極化碼在誤碼率性能上比基于3×3多維核矩陣[G3]的非系統極化碼更具有優勢;基于2×2核矩陣[G2]的系統極化碼也比基于3×3多維核矩陣[G3]的系統有更好的誤碼率性能。
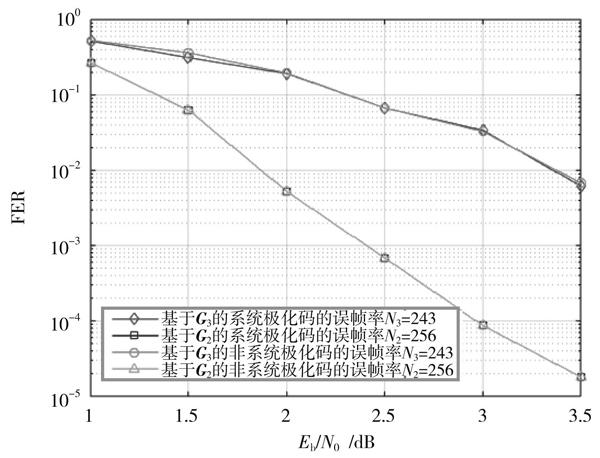
基于2×2核矩陣[G2]和3×3多維核矩陣[G3]的系統極化碼和非系統極化碼的誤幀率的仿真結果如圖2所示。
圖2 ?碼長[N2]=256和[N3]=243的系統極化碼和非系統極化碼的誤幀率

仿真結果表明,碼長類型為[N2=256]的系統極化碼和非系統極化碼分別比碼長類型為[N3=243]的系統極化碼和非系統極化碼具有更好的誤幀率性能。
綜上所述,根據基于CLAD的極化碼性能評估方法,能夠得出這樣的一個基本結論:基于2×2核矩陣[G2]的極化碼比基于3×3多維核矩陣[G3]的極化碼有更好的誤碼率和誤幀率性能。
3.2 ?碼長近似度[f=0.53]
如表1中所示,當[f=0.53],選取的一組碼長數值為[N2=128]與碼長[N3=243]。那么,將碼長[N2=128]視為與碼長[N3=243]相等,然后再直接進行這兩種碼長類型的極化碼之間的性能分析與判定。這里的仿真實驗是在AWGN下,對碼率為[12]、碼長[N]分別為243和128的極化碼進行的。調制方式為BPSK。SCL譯碼器的列表大小也設為32。
這里將碼長[N2=128]和[N3=243]視為等長。碼長[N2=128]和[N3=243]的系統極化碼和非系統極化碼的誤碼率的仿真結果如圖3所示。通過觀察圖3可知,碼長類型為[N3=243]的系統極化碼和非系統極化碼分別比碼長類型為[N2=128]的系統極化碼和非系統極化碼具有更好的誤碼率性能。由此,也許會判定基于3×3多維核矩陣[G3]的極化碼比基于2×2核矩陣[G2]的極化碼有更好的誤幀率性能。然而,這種情況與實際情況是不相符的。
圖3 ?碼長[N2=128]和[N3=243]的系統極化碼和非系統極化碼的誤碼率
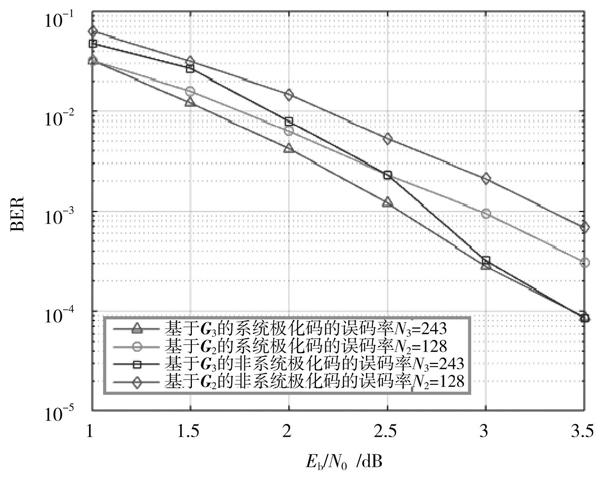
圖4 ?碼長[N2]=128和[N3]=243的系統極化碼和非系統極化碼的誤幀率

仿真結果表明,碼長類型為[N2=]128的系統極化碼和非系統極化碼分別比碼長類型為[N3=243]的系統極化碼和非系統極化碼在誤幀率性能上具有優勢。因而,可以判定基于2×2核矩陣[G2]的極化碼比基于3×3多維核矩陣[G3]的極化碼具有較好的誤幀率性能。
4 ?討 ?論
實際上,距離譜不能用來具體地分析極化碼的性能,但根據距離譜分析得出的性能上界卻能如實反映出基于2×2核矩陣[G2]和3×3多維核矩陣[G3]的極化碼之間的性能趨勢[2,4]。當[f=]0.95,仿真結果表明,基于2×2核矩陣[G2]的極化碼比基于3×3多維核矩陣[G3]的極化碼具有較好的誤碼率和誤幀率性能。根據距離譜的分析,這種情況與實際情況是一致的。當[f=]0.53,仿真結果表明的卻不是這種情況。至于誤幀率性能,[f=]0.95時的仿真結果比[f=]0.53時的仿真結果更符合距離譜分析所反映的誤幀率性能趨勢。
因此,這里可以得出另一個結論:碼長近似度[f]越大,極化碼性能評估方法的精度越高。碼長類型為[N5=5n]的極化碼的編譯碼是未來研究的重要課題,該方法也會因此得到進一步的驗證。
5 ?結 ?語
基于多維核矩陣的極化碼的構造理論及其應用尚待進一步的研究。當碼長近似度足夠大時,從本文提出的性能評估方法得出的判定結果與實際情況相符合。該方法還需要進一步的驗證,但對極化碼性能的評估與優化具有重要的借鑒意義和理論價值。
參考文獻
[1] ARIKAN E. Channel polarization: a method for constructing capacity achieving codes for symmetric binary?input memoryless channels [J]. IEEE transactions on information theory, 2009, 55(7): 3051?3073.
[2] LIU Zhenzhen, CHEN Kai, DONG Chao, et al. Performance analysis of polar codes based on 3×3 kernel matrix [C]// Proceedings of 2015 the 10th IEEE International Conference on Communications and Networking in China. Shanghai: IEEE, 2015: 382?386.
[3] KORADA S B, SASOGLU E, URNAKE R. Polar codes: cha?racterization of exponent of exponent, bounds, and construction [J]. IEEE transactions on information theory, 2010, 56(12): 6253?6264.
[4] LIU Zhenzhen, CHEN Kai, NIU Kai, et al. Distance spectrum analysis of polar codes [C]// Proceedings of 2014 IEEE Wireless Communications and Networking Conference. Istanbul, Turkey: IEEE, 2014: 490?495.
[5] RICHARDSON T, URBANKE R. Modern coding theory [M]. UK: Cambridge University Press, 2008.
[6] MORI R, TANAKA T. Performance of polar codes with the construction using density evolution [J]. IEEE communications letters, 2010, 56(12): 6253? 6264.
[7] ZHANG Liang, ZHANG Zhaoyang, WANG Xianbin. Polar code with block?length [N=3n] [C]// 2012 International Confe?rence on Wireless Communications and Signal Processing. Huangshan: IEEE, 2012: 1?6.
[8] TAL I, VARDY A. List decoding of polar codes [J]. IEEE transactions on information theory, 2012, 61(5): 2213?2226.
[9] CHEN Kai, NIU Kai, LIN Jiaru. Improvement successive cancellation decoding of polar codes [J]. IEEE transactions on communications, 2013, 61(8): 3100?3107.
[10] ARIKAN E. Systematic polar codes [J]. IEEE communications letters, 2011, 15(8): 860?862.

