橫向分布載荷作用下雙模量簡支梁的級數解

韓朝暉

（湖南文理學院，湖南 常德 415000）

0 引言

隨著新材料的不斷涌現，有許多材料受拉和受壓時變形模量相差較大，在不同應力狀態下需要考慮其不同的本構關系，成為了當前研究熱點，吸引了廣大學者注意力。Medri G建立了考慮受拉受壓不同變形模量各向同性材料的非線性模型[1]、Bert CW等[2]、Srinivasan RS[3]研究了受拉受壓不同變形模量材料板的振動；李戰莉等[4]、曾紀杰[5]、蔡來生等[6]建立了受拉受壓不同變形模量材料的本構關系；吳曉等[7]考慮材料的雙模量特性，分析了雙模量圓板的彎曲變形；羅戰友等[8]建立了不同拉壓模量及軟化特性材料的柱形孔擴張問題的統一解；Ambartsumyan SA[9]、高潮等[10]和吳曉等[11-12]對不同拉壓模量板、梁[13-14]的彈性理論解開展了研究；吳曉等[15]和韓朝暉等[16-18]考慮剪切效應建立了不同拉壓模量材料的彈性理論。本文考慮雙模量材料特性，利用奇異函數對分布載荷作用下不同拉壓模量梁的平面應力問題進行了研究，

并推導出了雙模量簡支梁應力公式的級數解。

1 應力函數

如圖1所示雙模量簡支梁。

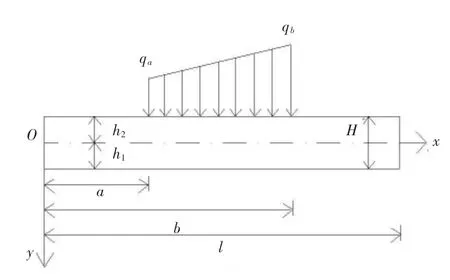
圖1 雙模量簡支梁

其拉伸區和壓縮區的應力函數應滿足協調方程：

式中：i=1時代表拉伸區，i=2時代表壓縮區。以下類同。令式（1）的解為

將式（2）代入式（1）可得

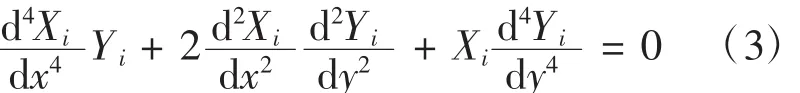
由式（3）可得

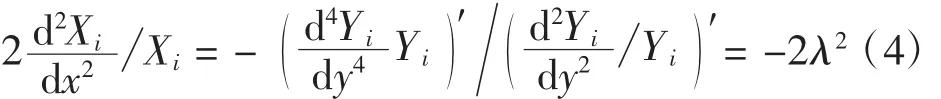
由式（4）可以求得：

將式（6）代入式（3）可得

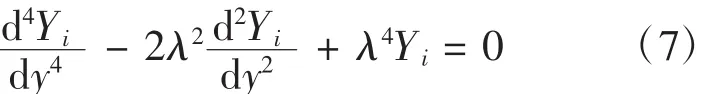
由式（7）可以求得

所以，雙模量簡支梁的應力函數為

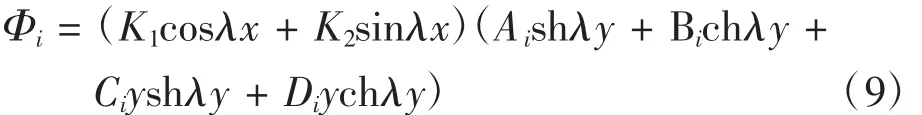
對于圖1所示雙模量簡支梁，在梁兩端x=0和x=l時，有

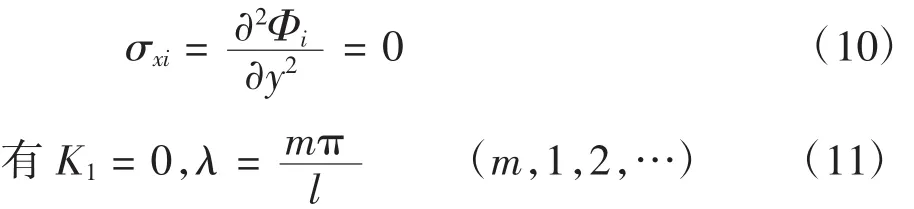
故圖1所示雙模量簡支梁應力函數通解為

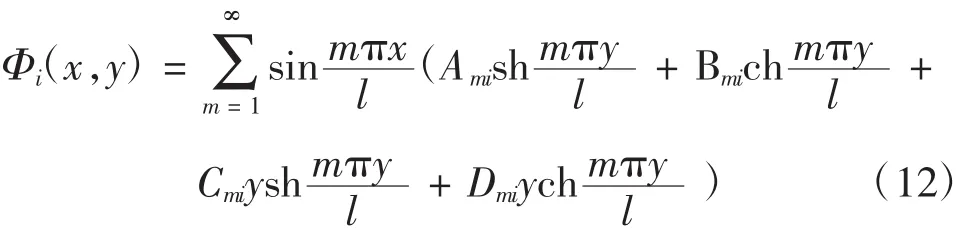
2 應力公式

對于圖1所示工程中常見的線性分布載荷可用奇異函數表示為如下形式：

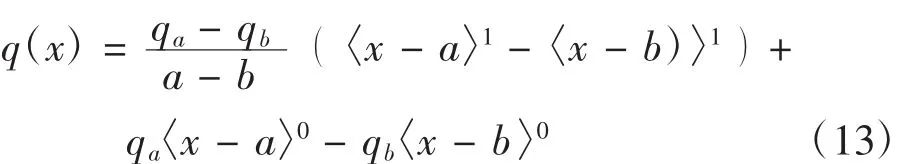
其中，奇異函數運算規則為

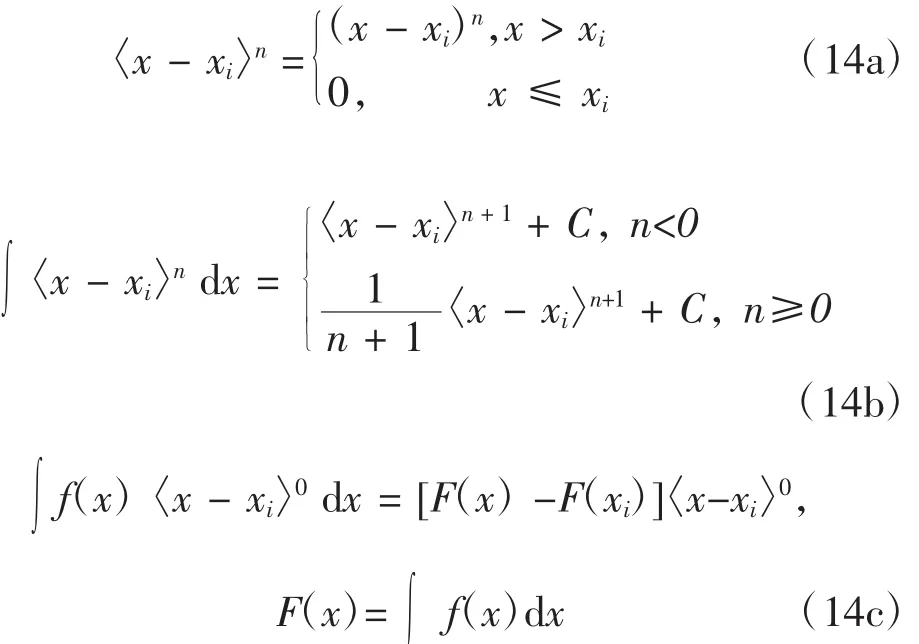
利用傅里葉級數可把式（13）展開為如下形式：

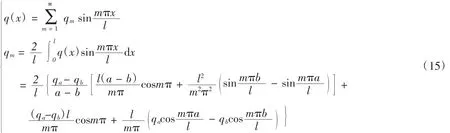
由式（12）可知雙模量簡支梁拉伸區和壓縮區的應力分別為：

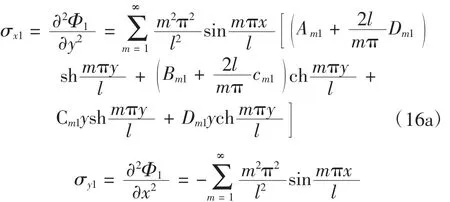
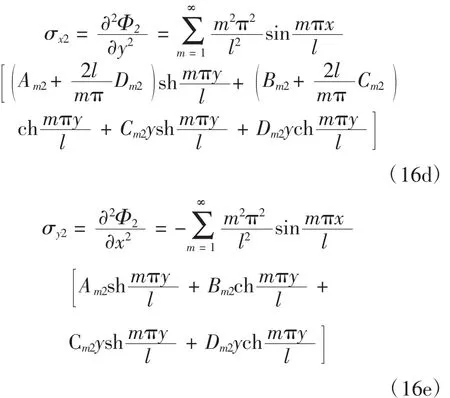
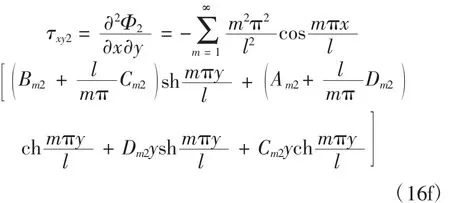
雙模量簡支梁的邊界條件及中性層連續條件分別為

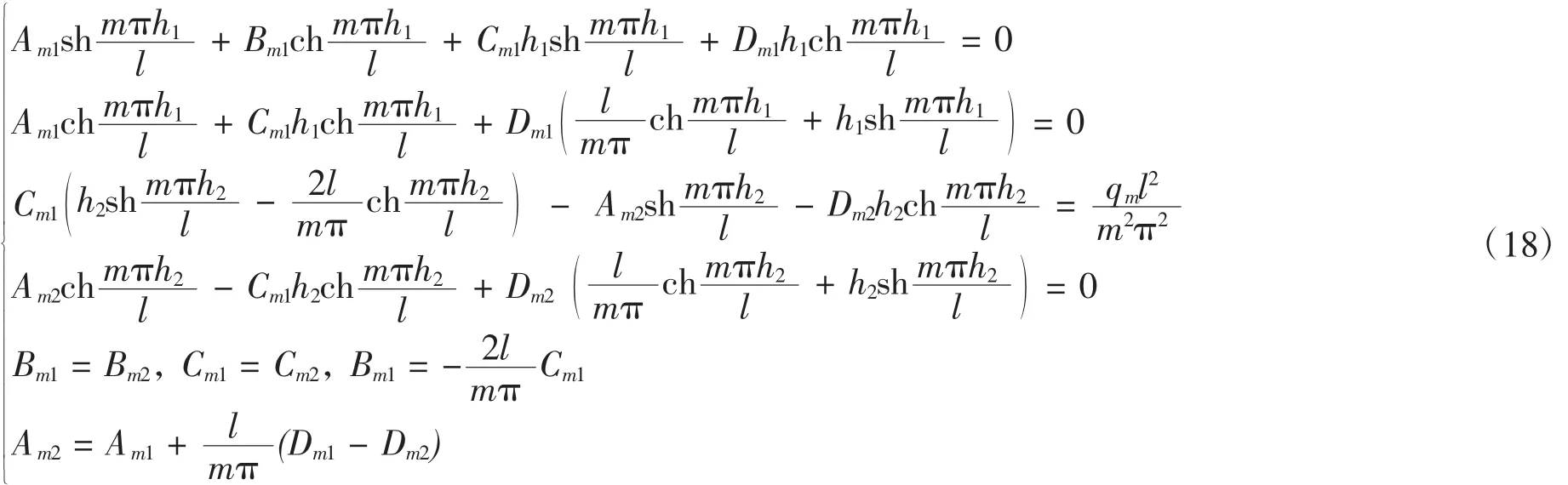
將（16）代入式（17）可得

利用式（18）可以求得

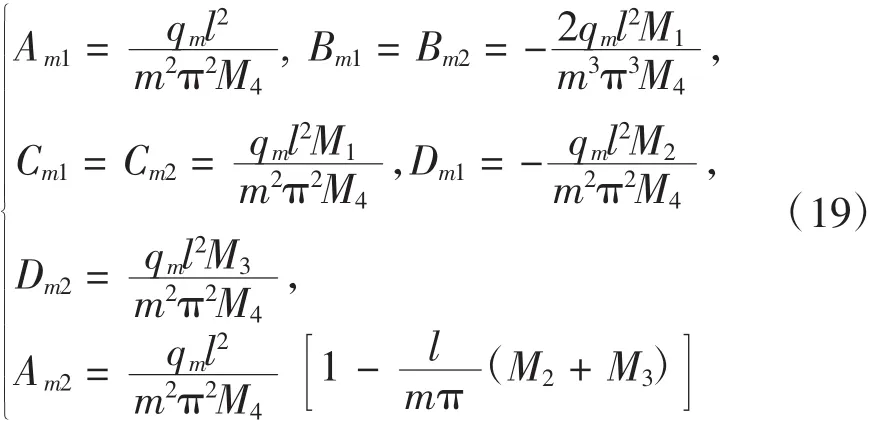
式中：

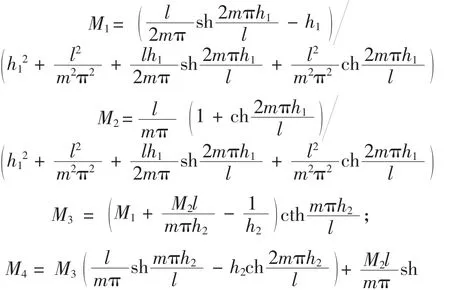
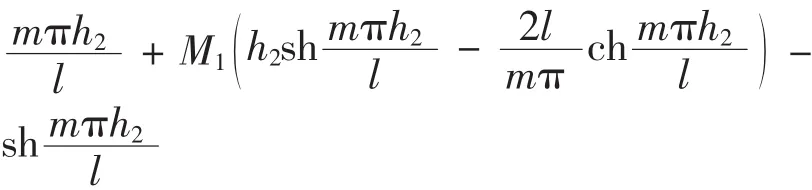
將式（19）代入式（16）即可得到雙模量簡支梁在橫向分布載荷作用下的應力表達式。

3 中性軸位置的確定

雙模量梁在外荷載作用下彎曲時的應力和應變關系為

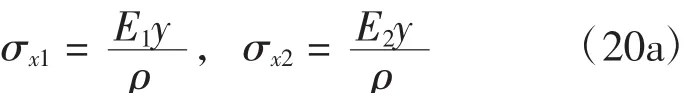
式中：E1為拉伸區的彈性模量；E2為壓縮區的彈性模量。

如圖2所示任意荷載作用下的簡支梁，對B點的力矩平衡方程為

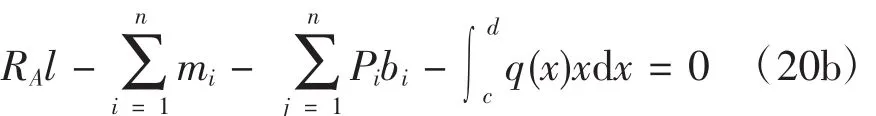
所以，

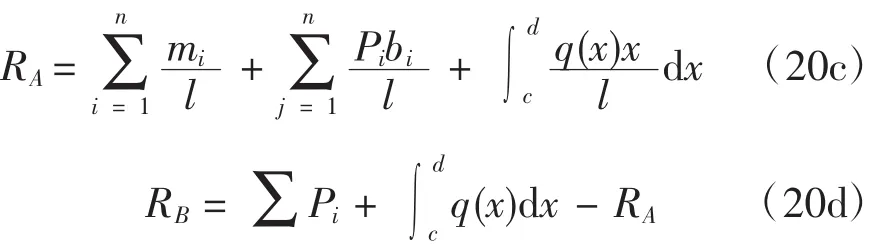
圖2 任意荷載作用下簡支梁

這樣，由簡支梁的支座反力，就可以得到各個截面的彎矩表達式。

彎曲時雙模量梁的力矢和力矩平衡方程分別為：

將式（20）代入（21）中，可得

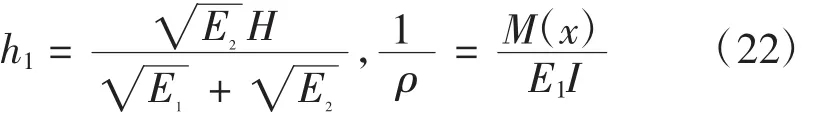
式中：h1為拉伸區高度；h2為壓縮區高度；H=

由式（22）可知，雙模量梁中性軸的位置與作用在梁的橫向載荷無關。

4 算例分析與討論

設某雙模量簡支梁的b=1，E1=93.2 GPa，E2=124.36 GPa。采用本文方法計算中點處的最大拉應力及最大壓應力，如表1~表4所示。

為驗證本文方法，采用ANSYS有限元程序對雙模量簡支梁中點處的最大拉應力及最大壓應力也進行了計算，結果一并列入表1~表4。

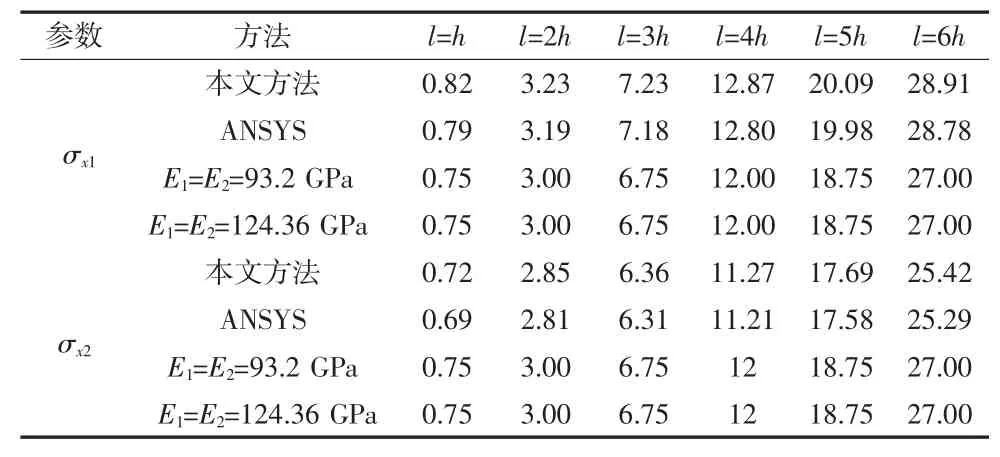
表1 qa=qb，a=0，b=l時雙模量簡支梁中點處彎曲應力

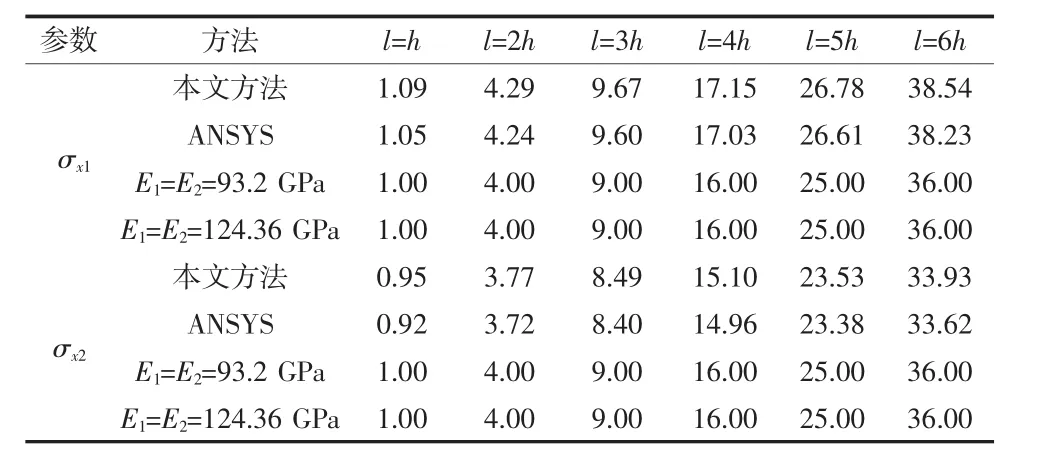
表2 qb=2qa，a=0，b=l時雙模量簡支梁中點處彎曲應力

表 3 qa=qb，a=，b=l時雙模量簡支梁中點處彎曲應力

表 3 qa=qb，a=，b=l時雙模量簡支梁中點處彎曲應力

參數 方法 l=h l=2h l=3h l=4h l=5h l=6h σx1本文方法 0.72 2.83 6.35 11.27 17.58 25.29 ANSYS 0.69 2.79 6.28 11.21 17.49 25.18 E1=E2=93.2 GPa 0.65 2.63 5.91 10.50 16.41 23.63 E1=E2=124.36 GPa 0.65 2.63 5.91 10.50 16.41 23.63 σx2本文方法 0.63 2.49 5.59 9.89 15.49 22.25 ANSYS 0.60 2.45 5.52 9.80 15.38 22.13 E1=E2=93.2 GPa 0.65 2.63 5.91 10.50 16.41 23.63 E1=E2=124.36 GPa 0.65 2.63 5.91 10.50 16.41 23.63

表 4 qb=2qa，a=，b=l時雙模量簡支梁中點處彎曲應力

表 4 qb=2qa，a=，b=l時雙模量簡支梁中點處彎曲應力

注：表1~表4中E1=E2=93.2 GPa、E1=E2=124.36 GPa是材料力學方法。

參數 方法 l=h l=2h l=3h l=4h l=5h l=6h σx1本文方法 0.95 3.77 8.48 15.02 23.45 33.71 ANSYS 0.92 3.71 8.39 14.91 23.29 33.45 E1=E2=93.2 GPa 0.88 3.50 7.88 14.00 21.88 31.50 E1=E2=124.36 GPa 0.88 3.50 7.88 14.00 21.88 31.50 σx2本文方法 0.82 3.30 7.43 13.20 20.58 29.68 ANSYS 0.80 3.26 7.35 13.09 20.46 29.42 E1=E2=93.2 GPa 0.88 3.50 7.88 14.00 21.88 31.50 E1=E2=124.36 GPa 0.88 3.50 7.88 14.00 21.88 31.50

本文把雙模量梁應力公式的級數解、有限元法、材料力學方法計算的結果均列在表1~表4中，以便分析對比三種方法計算結果的計算精度。

由表1~表4可知，采用奇異函數研究分布載荷作用在雙模量簡支梁上任意梁段上的彎曲變形都是很方便的。本文方法與有限元法的計算結果相差不大，驗證了本文方法的正確性。

相同彈性模量彈性理論與本文雙模量簡支梁中點處彎曲應力的級數解誤差均在5%以上。對于雙模量梁而言，采用單模量彈性理論研究雙模量梁的彎曲應力，拉壓區的彎曲應力絕對值是相等的，因為單模量彈性理論確定的梁的中性軸位置是在梁橫截面高度的中點處。而事實上，雙模量梁的拉壓區的彎曲應力絕對值是不相等的，是隨雙模量簡支梁拉壓區的彈性模量變化而變化的，即雙模量彈性理論確定的梁的中性軸位置不在梁橫截面高度的中點處，從而導致雙模量梁的拉壓區的彎曲應力絕對值不相等。在本文中，雙模量簡支梁的拉壓區的彎曲應力相差均達10%以上。所以，雙模量簡支梁的平面應力問題，不宜采用相同彈性模量彈性理論，而應該采用雙模量彈性理論。

由于長高比的增大使得彎矩變大，因而，在外載荷作用下，雙模量簡支梁的彎曲應力隨著長高比的增大而增大。

由于分布載荷作用下的彎矩大于均布載荷，相應的，雙模量簡支梁中點處的彎曲應力大于均布載荷。

由表3、表4可以看出，對于拉伸區的彎曲應力，材料力學方法與本文方法計算結果相差不大，壓縮區的彎曲應力則誤差較大，大于50%，說明了材料力學方法計算雙模量簡支梁的彎曲應力的局限性。

5 結論

（1）采用奇異函數研究分布載荷作用在雙模量簡支梁上任意梁段上的彎曲變形都是很方便的。本文證明了雙模量梁中性軸的位置與作用在梁的橫向載荷無關。

（2）采用奇異函數研究雙模量簡支梁彎曲應力，具有較高的計算精度。

（3）對于拉壓彈性模量相差較大的簡支梁，其平面應力計算要采用雙模量彈性理論。

（4）在外載荷作用下，雙模量簡支梁的彎曲應力隨著長高比的增大而增大；均布載荷作用下的彎曲應力小于分布載荷作用。