計算受限控制系統的一種全資源預測控制方法
馬翠芹 姚俊毅 韓康 趙云波
近年來,物聯網、信息物理系統、工業互聯網及其應用領域,例如智慧家居、車聯網、智慧工廠等各種智能互聯系統得到了迅猛的發展.這種發展得益于通信和計算兩種技術的巨大進步,一方面,通信技術的進步,特別是無線通信網絡的發展,使得信息流動更容易,成本更低,促進了大規模互聯系統的構建;另一方面,計算能力的進步,特別是微型嵌入式計算芯片的發展,使得更多的微型設備也可以具有計算能力,為系統的智能化發展提供了物質基礎[1?6].無線通信和嵌入式計算等技術在控制系統中的廣泛使用為控制系統設計和分析提出了新的挑戰,也促使了各個不同但相關的研究領域的出現和發展.從考慮各種通信網絡在控制系統信息傳輸中的作用的角度,出現了網絡化控制系統的概念,該領域在過去近20年的大量研究為包含通信網絡因素的控制系統的設計和分析奠定了堅實的基礎[7-10];從考慮多個設備間互聯及其拓撲結構和群體行為的角度,為多自主體系統的研究提供了一個重要的模型基礎[11-12];從物理系統和信息系統交互影響的角度,信息物理系統的研究也在近些年蓬勃發展起來[13-14].
與上述角度不同,本文關注各類智能系統中大量采用的微型處理器及其帶來的計算能力限制問題.事實上,各類智能系統以多個具有有限計算和通信能力的設備的互聯互通為基本特征,勢必導致其計算能力成為關注的焦點,一方面運行控制器設備本身的計算能力有限,另一方面又要在互聯的設備間共享計算資源,使得對某特定的控制系統而言,其控制器的可用計算資源成為有限時變且不可預測[15?16].
傳統控制系統的可用計算資源很少有不可預測的特點.因為傳統控制系統往往不存在大量設備的互聯,從而在系統邊界上是封閉的,即控制系統的各個組件對該系統是私有的.因此,即便計算資源有限時變,這一變化特點在控制系統的范疇內也往往是事先預知的.而對已知的時變資源的分配可以采用各種資源調度的算法進行有效處理[17-19].
在本文研究的問題中,對于提供計算能力的設備,仍依賴調度算法對該設備的計算資源進行全局分配,但是,因為全局調動算法的分配很難實時準確地將控制系統的需要考慮在內,分配給控制系統的可用計算資源就難免具有有限時變且不可預知的特點.有限時變的特點意味著在某些時刻控制系統可能會因為計算資源太少而無法運行控制器,使得系統開環,在極端情況下可造成系統失穩,而不可預測的特點又使得任何離線設計的方法失效.這使得不考慮這一新特性的傳統控制方法很難在這種新情境下有效發揮作用,從而要求一種全新的在線控制框架來處理這一問題.
本文面向計算受限控制系統提出一種全資源預測控制策略及相關控制器設計方法.該策略注意到了有限時變可用計算資源的另一個可能特點,即在某些時刻可用計算資源可能極為充足,在運行控制器外還有大量剩余,因此就可以使用這些充足剩余的計算資源進行控制量的前向預測,這些控制預測量進而能夠在控制系統可用計算資源不足時閉合系統.這一策略僅使用已分配給控制系統的計算資源,但通過對其更充分的利用可獲得更好的控制系統性能.
本文結構安排如下:第1節嚴格定義所考慮的問題;第2節提出全資源預測控制策略;第3節提供了一種改進的模型預測控制算法作為該策略所要求的控制器的一種具體實現;第4節使用基于MATLAB的數值仿真和MATLAB/LabVIEW聯合仿真對提出的策略和算法進行驗證;第5節總結全文.
1 問題描述
考慮圖1所示的控制系統,其受控對象由離散時間多輸入多輸出線性時不變系統描述.
在圖1中,控制器通過計算能力受限的某嵌入式處理器實現,并且該處理器同時負責其他系統(可能并非控制系統)的計算任務.這一模型的提出受近些年快速發展的無線傳感網絡和信息物理系統等類系統的啟發,該類系統具有計算能力受限的設備大規模互聯使用的基本特征.該模型意味著分配給所考慮的控制系統的計算資源一方面是有限的,因為處理器的計算能力本身有限,另一方面又呈現出不可預知的時變特性,因為該計算能力與所考慮的控制系統外的其他系統和設備共享,造成該計算能力在所考慮控制系統的邊界之外而無法有效管理.
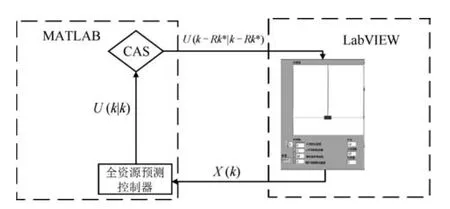
圖1 具有時變不可預知計算資源的控制系統Fig.1 Control systems with time-varying and unpredictable computational resources
如果用R(k)表示k時刻分配給所考慮控制系統的可用計算資源,用R?表示處理器的總計算資源,則有

將計算控制信號u(k)所需的最小計算資源記為,則應有,否則該處理器的最大計算能力都不足以運行控制器,也就是對控制系統而言完全不可用.在時刻k控制量可被計算的條件是在此時刻控制系統可使用的計算資源不小于所要求的最小計算資源,即

如式(3)不滿足,則控制信號u(k)無法計算.若式(3)太長時間不被滿足,則系統將很可能因為保持開環太長時間而不穩定,這在實際系統中是不允許的.
式(2)和式(3)可合并為式(4),這是傳統控制方法能夠使用的前提條件.

然而,可用計算資源的時變特性意味著在某些時刻R(k)會太過有限而不能計算控制信號,即
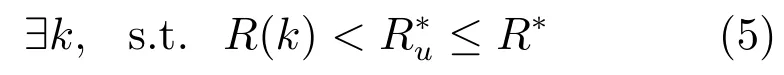
為了解決上述問題,一種可能的解決方案是對計算資源進行全局調度.然而,調度算法在該問題中難以見效,原因有二:1)在處理器的計算資源是有限的并且共享的系統和設備對處理器計算資源要求較高的前提下(這是本文考慮問題的出發點),式(4)中的計算資源要求不可能對所有時刻都滿足(否則傳統控制方法即可滿足要求),意味著式(5)中的情形總會出現(在這些情形時傳統控制方法失效);2)調度算法通常無法將控制系統的實時計算資源要求考慮在內,因此,或者會分配計算資源過少造成式(5)中的情形,或者太過保守將非必需的寶貴的計算資源分配給控制系統而造成浪費,也就是會出現如下情形:
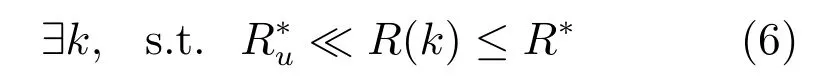
綜合上述討論,本文考慮如下問題:
問題1.考慮如圖1所示的控制系統,其中控制系統可用計算資源是有限時變而不可預知的,即在某些時刻會太少而不能執行控制器的計算(式(5)),而在其他一些時刻在執行完控制器計算后還有大量剩余(式(6)).設計控制策略以有效使用計算資源,提升控制系統性能.
注1.圖1中嵌入式處理器的有限計算資源在控制系統的控制器和其他可能的共享設備中通過某種調度算法進行分配.本文并不研究這些計算資源的調度算法,而是在一定的計算資源調度算法下,研究如何對分配給控制系統的有限時變而不可預知的計算資源進行高效的使用.在這個意義上,本文所做的研究并非是計算資源調度算法的替代,而是其在控制系統應用場景下的補充.
2 全資源預測控制策略
本節首先討論控制系統可用計算資源與控制預測步長的一個基本關系,隨之給出全資源預測控制策略的描述,最后討論使用該策略的算法性能和閉環系統的穩定性.
2.1 可用計算資源與控制預測步長
本節的討論主要基于如下事實[20]:控制器所需的計算資源隨著控制預測步長的增加而嚴格增加.注意到計算資源一般由分配給的處理器時間來衡量,在不引起誤解的前提下,用R(k)自身表示在k時刻分配給控制系統的處理器時間,從而,這里是非負實數集.記計算控制預測步長i所需最小計算資源為(從而),有如下的從可用計算資源到控制預測步長的映射,f:,其中是非負整數集.
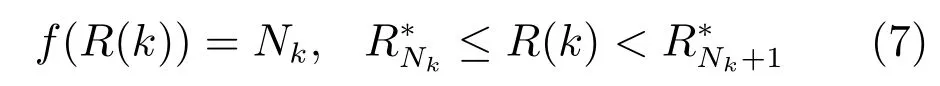
式(7)說明,對時刻k的任意可用計算資源,將有唯一的控制預測步長Nk與之對應.可以注意到,函數f(·)是分段常值且右連續的.
式(7)中的映射提供了看待控制系統可用計算資源R(k)的另一個視角,即它可以被等價看作計算資源可以處理的控制預測步長Nk.另外,從式(5)和式(6)可以得出:1)若式(5)成立,則Nk=0;2)若式(6)成立,則Nk?1.
前一個條件Nk=0使得傳統控制算法在此處失效,因為可用的計算資源連一步控制信號都無法算出(要求Nk≥1,?k),而后一個條件Nk?1則提供了更為有效利用可用計算資源的可能性.注意到在這種情況下,利用可用計算資源可以計算多步控制信號.
注2.式(7)中的映射是依賴具體的控制算法的.若控制算法本身復雜度高,則由R(k)映射到的Nk值較小,否則Nk值較大.但這并不影響這一映射的基本形式和Nk隨R(k)遞增且函數f(·)是分段常值且右連續的基本性質,因此也并不影響本文后續的討論.
2.2 全資源預測控制策略及算法
本文提出的針對計算受限控制系統的全資源預測控制策略的基本架構見圖2.
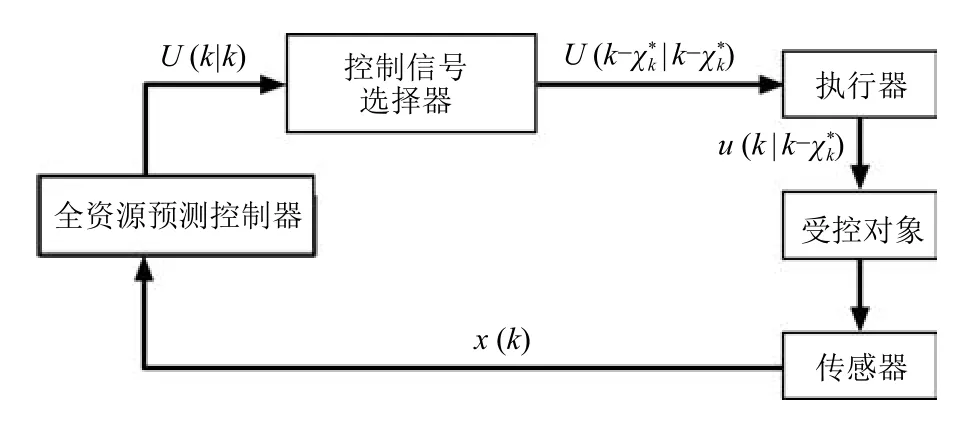
圖2 面向計算受限控制系統的全資源預測控制策略Fig.2 The full resource predictive control strategy for control systems subject to computational constraints
傳統控制方法僅計算當前時刻的控制量,而在本文的全資源預測控制策略中,可用的計算資源被充分使用計算盡可能多的前向預測控制量.這些預測控制量進而存儲在執行器端以備使用.依照式(7)中的映射,并記基于k時刻信息計算的k+i時刻的控制預測量為u(k+i|k),i=0,1,···,Nk,則k時刻的前向預測控制序列可構建如下:
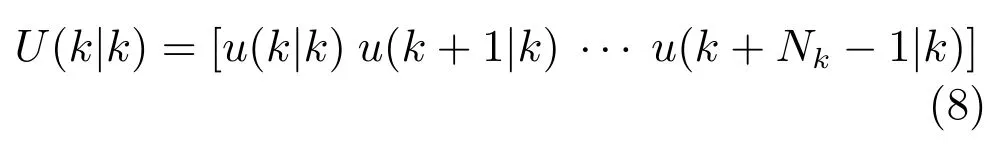
圖2中的控制信號選擇器包含兩個部件:1個寄存器,能夠存儲最大可能長度的前向預測控制序列;1個簡單的邏輯電路,可以用來選擇合適的控制信號.控制信號選擇器按如下方式工作:
1)在新的前向控制預測序列到達時更新寄存器,保證寄存器中的前向控制預測序列總是最新的.由于式(5),寄存器中k時刻的前向控制預測序列并不一定是在當前時刻計算的.記k時刻寄存器中的前向控制預測序列已經在其中存儲了步,k時刻的前向控制預測序列則是在時刻計算,可寫為.
2)在當前計算資源不足無法計算控制信號時,從前向控制預測序列中選取合適的替代控制量.使用上面符號,k時刻從中選取的控制量為
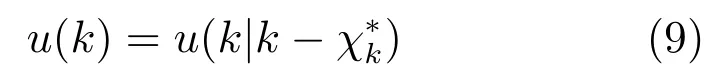
為使得在任何時刻從前向控制預測序列中都有控制量可用,可用計算資源需滿足一定條件,如推論1所述.這也是此后所提算法1能夠工作的前提條件.
推論1.若下式成立:
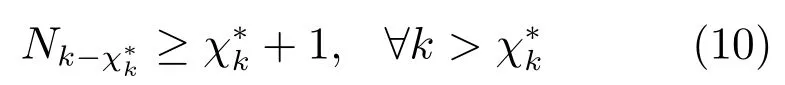
則式(9)中的控制量總在控制信號選擇器中可供選擇.
證明.注意到k時刻的前向控制預測序列U(k是在時刻計算的. 為了使得按照式(9)選取的控制量在中,前向控制預測序列的長度,即,需大于或等于k,這正是推論中給出的條件.□
注3.考慮如下兩種推論1的特例情況.
所提出的策略總結為算法1,采用該算法的系統整體架構見圖2.
算法1.全資源預測控制策略
步驟1.傳感器采樣系統狀態并將采集數據傳輸至控制器;
步驟2.由可用計算資源R(k)按照式(7)獲得可計算的控制預測步長Nk,進而按照式(8)計算前向控制預測序列并將之傳至執行器;
步驟3.控制信號選擇器更新寄存器,按式(9)選擇控制量并令執行器執行控制量.
注4.算法1并未考慮計算時間導致的時延.因為與控制系統的時間尺度相比,該計算時延往往是足夠小且可以忽略的.不過,需要指出的是,如果絕對必要,這一時延可以放入到執行器的等待時延中,因此可以在不更改系統架構下進行有效處理.
注5.算法1僅對已經分配給控制系統的計算資源做有利于控制系統性能的合理使用,其權限局限于控制系統本身.對整個嵌入式處理器的計算資源的分配需由上一級機構,即計算資源的調度算法做出.本文的全資源預測控制策略是在此意義下對計算資源調度的一個有效補充.
2.3 算法1性能討論
傳統控制方法在無法獲得當前控制信號時,往往或者使用零階保持(即保持先前的控制輸入),或者采用零控制(使系統臨時開環).這樣,面對本文考慮的計算資源有限的控制系統,使用傳統控制方法實際所采用的控制信號如下:

與之相對應的,采用全資源預測控制策略的實際控制信號由式(9)給出,或等價地寫為
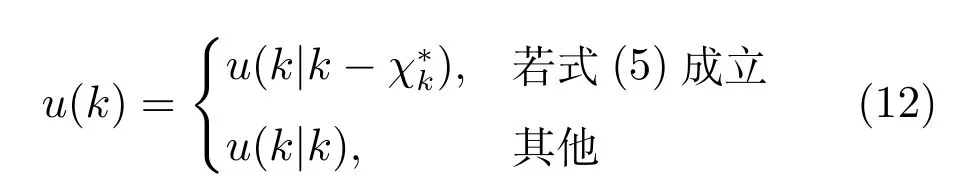
從式(11)和式(12)可以看出,在控制系統被分配的計算資源充足時,就實際使用的控制信號而言,使用或不使用本文提出的全資源預測控制策略并無區別;但是,在當前計算資源不足以進行控制計算時(即式(5)成立),本文策略提供了額外的自由度,使得可以針對具體情形設計式(8)中的前向預測控制序列對本來缺少的控制信號進行替代補償.
從這一角度來說,本文提出的全資源預測控制策略通過充分使用分配給的計算資源(而并不要求更多),可以實現至少不差于傳統控制所帶來的控制性能 (使或 0),但通過合理設計式(8)中的前向預測控制序列U(k|k),提供了提升控制系統性能的自由度和可能性.
另外,式(8)中的前向預測控制序列U(k|k)僅是一種一般形式,針對具體形式和目標的系統還需要具體的設計.事實上,只要可以產生所需的前向控制預測序列,它允許所有可能的控制器設計方法.例如,在第3節給出了一種基于改進的模型預測控制的設計方法.進一步,從U(k|k)的一般性上說,所提出的全資源預測控制策略可用于任意受控對象,而并不局限于線性系統模型,本文采用線性對象僅為了后續系統分析和具體前向預測控制序列實現的方便.
2.4 閉環系統穩定性
采用算法1的控制系統所使用的控制信號由式(8)和式(9)給出.但是,式(8)中預測控制序列U(k|k)的設計是一個開放問題,并沒有事先規定任何特定形式,因此閉環系統的具體形式和相應的閉環穩定性分析就難以一般性的給出.另一方面,控制系統的可用計算資源由上層調度機構給出,很多情況下可能無法事先估計,這導致了對可用計算資源(進而)定量描述的缺乏,也使得一般性的閉環系統穩定性分析較難進行.
為了能夠探討閉環系統的穩定性,考慮一種簡單情況.首先假設預測控制序列U(k|k)采用狀態反饋的情況.此時實際使用的控制信號也具有狀態反饋的形式,即
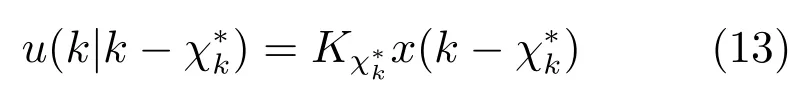
閉環系統進而具有如下形式:
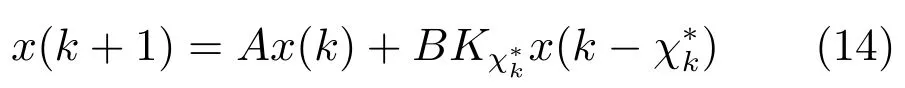
其次,有理由假設分配給控制系統的計算資源不是一直缺乏的,那么存儲在寄存器中的前向預測控制序列就總可以在有限時間內得到更新.即存在某上界NR,使得.進而,可構建增廣系統狀態X(k)為
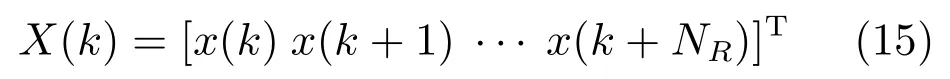
閉環系統(14)的增廣形式可寫為
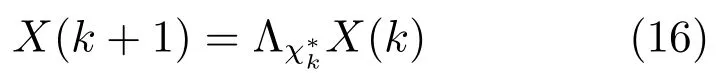
其中,Λχ?k由A,B,等參數確定.
將上述系統視為一般的切換系統,則可以利用標準切換系統方法在李雅普諾夫理論和線性矩陣不等式框架下得到其穩定性條件.該理論方法已經較為成熟,在相關文獻中有更多的技術細節.
需要指出的是,上述穩定性分析基于對控制律的狀態反饋形式假設,并不具有普適性,所得結論也很難對前向控制預測序列的設計提供好的指導意義,實際應用中閉環系統的穩定性尚需在具體的控制律設計方法給出后另行具體分析.不過,盡管在此并未給出閉環系統穩定的一般結論,但由前面兩小節的分析可以看出,U(k|k)設計所帶來的自由度可保證采用算法1的控制系統性能(也包括閉環穩定性)永遠不差于常規方法.如何針對具體系統進行具體設計將是后續的主要工作.
3 基于改進模型預測控制的前向控制預測序列計算
如前所述,前向預測控制序列U(k|k)需針對所考慮系統具體化.針對本文所考慮系統形式(1),本節提出一種改進的模型預測控制設計方法作為U(k|k)的一種具體實現方法.經典模型預測控制是一種有限時域優化控制方法,通過優化有限步長的系統軌跡來求取一串控制序列,然后將其中的第1步用于實際控制.通過在每一步的滾動優化,模型預測控制方法可以處理噪聲、不確定性和其他限制[21].
模型預測控制的目標函數一般定義如下:
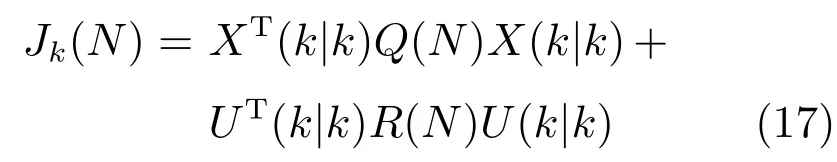
其中,Jk(N)是k時刻的目標函數,定義于式(8)的U(k|k)=[u(k|k)···u(k+N?1|k)]T是需確定的控制預測序列,X(k|k)=[x(k+1|k)···x(k+N|k)]T是預測狀態軌跡,Q(N)和R(N)是權重矩陣,N為預測時域.
上述優化問題的計算復雜性主要決定于預測時域N.記解決預測時域為N的優化問題所需的最小計算資源為RJN,式(7)中所定義的函數f(·)可對目標函數(17)進一步具體化如下:
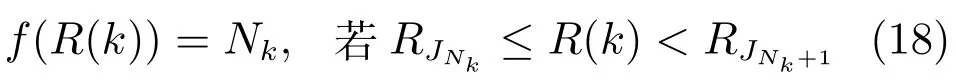
依照式(18),在如下討論中將以Nk指代控制系統的可用計算資源R(k).
從式(18)得到的具體形式的f(·)意味著帶目標函數(17)和N=Nk的優化問題可以在時刻k使用可用計算資源求解.為解決優化問題,k時刻的預測狀態可遞歸求解如下:
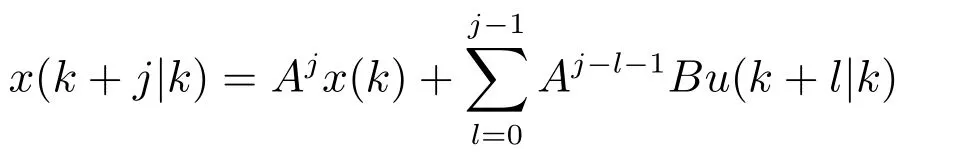
定義E(Nk)=[AT···(ANk)T]T,F(Nk)是Nk×Nk下三角矩陣塊,其非零項定義為F(Nk)ij=Ai?jB,j≤i.則上式的向量形式可表示為
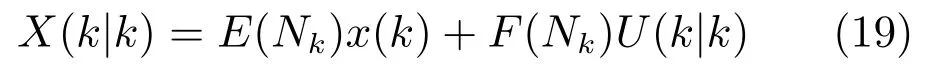
最優的前向控制預測序列可以通過將式(19)代入式(17)并最小化Jk(Nk)得到,其解具有如下的狀態反饋形式:

其中,
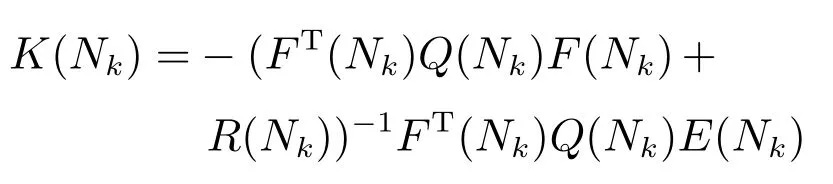
使用如上的改進模型預測控制方法進行全資源預測控制的步驟總結為算法2.
算法2.基于改進模型預測控制的全資源預測控制算法
步驟1.傳感器采樣系統輸出并將數據傳輸至控制器;
步驟2.基于分配的計算資源R(k),依照式(18)決定前向控制預測序列的步長Nk,通過式(20)計算前向控制預測序列并將之傳至執行器;
步驟3.控制選擇器更新其寄存器并依照式(9)選擇合適的控制量并令執行器應用至系統.
注6.本節中的改進模型預測控制算法在兩個方面不同于傳統模型預測控制.首先,算法2中的預測時域是時變的并決定于可用計算資源R(k).其次,傳統模型預測控制只使用所計算的控制序列中的第一個,而算法2卻利用了所有可能的前向控制預測.
4 仿真算例
本節通過如圖3所示的小車–倒立擺系統對所提出的全資源預測控制策略和算法進行驗證.該系統可建模為式(1)中的線性系統,其系統矩陣如下:
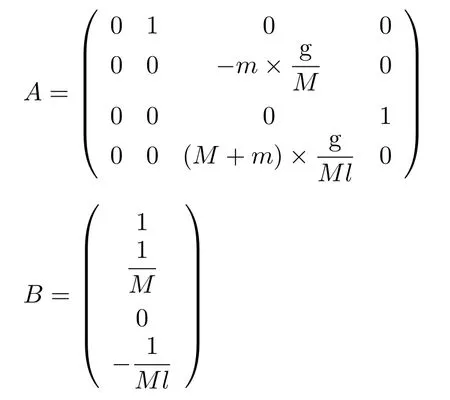
其中,狀態變量x(k)=[x1(k)x2(k)x3(k)x4(k)]T且x1(k)為小車的位移,x2(k)為小車的速度,x3(k)為倒立擺與垂直方向的夾角或偏離角度,x4(k)為剛性擺桿的角速度.各物理量都具有相應的單位,其值如下:小球的質量m=1,小車的質量M=10,剛性擺長度l=10,重力加速度g=9.8.
為了驗證提出的控制策略的有效性,考慮兩種情況的比較,兩種情況都使用第3節提出的模型預測控制器,但一種使用第2節提出的全資源預測控制策略,另一種則不使用.也就是說,前者可利用存儲在前向控制預測序列中的預測控制量,而后者在可用計算資源無法進行控制計算的時候,即R(k)<時,只能使用零控制,而在其他時刻則如傳統模型預測控制一樣使用預測序列的第1個控制量.

圖3 小車–倒立擺系統示意圖Fig.3 The vehicle and inverted pendulum system
首先進行基于MATLAB的數值仿真,進而采用MATLAB/LabVIEW相結合的聯合仿真方法進行驗證.
例1.基于MATLAB的數值仿真
將計算資源用整數表示,并設處理器的最大計算資源R?=100.設控制系統進行1~7步控制預測所需的最小計算資源如下:
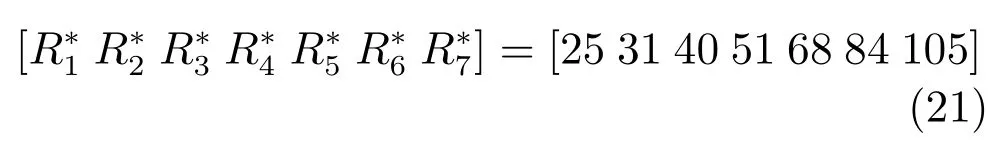
控制系統的可用計算資源R(k)假設為某一馬爾科夫過程,并具有較高的概率小于(見式(5))或接近R?(見式(6)).在實際中,已分配計算資源的突然大幅度切換較為少見,因此在下一時刻控制系統的可用計算資源有較高概率仍保持在原有或相近水平.在R(k)的轉移概率矩陣中本文也將此特性考慮在內.
在上述系統設置下,控制系統可用計算資源R(k)的典型時間演化可見圖4(a).由式(21)可知,前向控制預測序列的長度Nk可由計算資源R(k)來確定,如圖4(b)所示.另外,從圖4(c)中χ?k的演化可看出,可用計算資源經常會太少不足以計算任何控制量,這使得傳統控制方法無法在這種情況下工作.
圖5(a)的系統響應支持本文期望的結論:在不增加任何計算消耗的前提下,使用我們的控制策略的系統狀態響應更快的到達穩定,并較少波動.圖5(b)也顯示采用我們的控制策略的實際控制量也更為平滑.
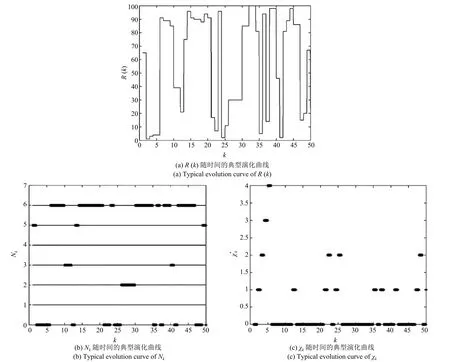
圖4 MATLAB仿真的R(k),Nk和χk隨時間的典型演化曲線Fig.4 Typical evolution curves ofR(k),Nkandχkin MATLAB simulation
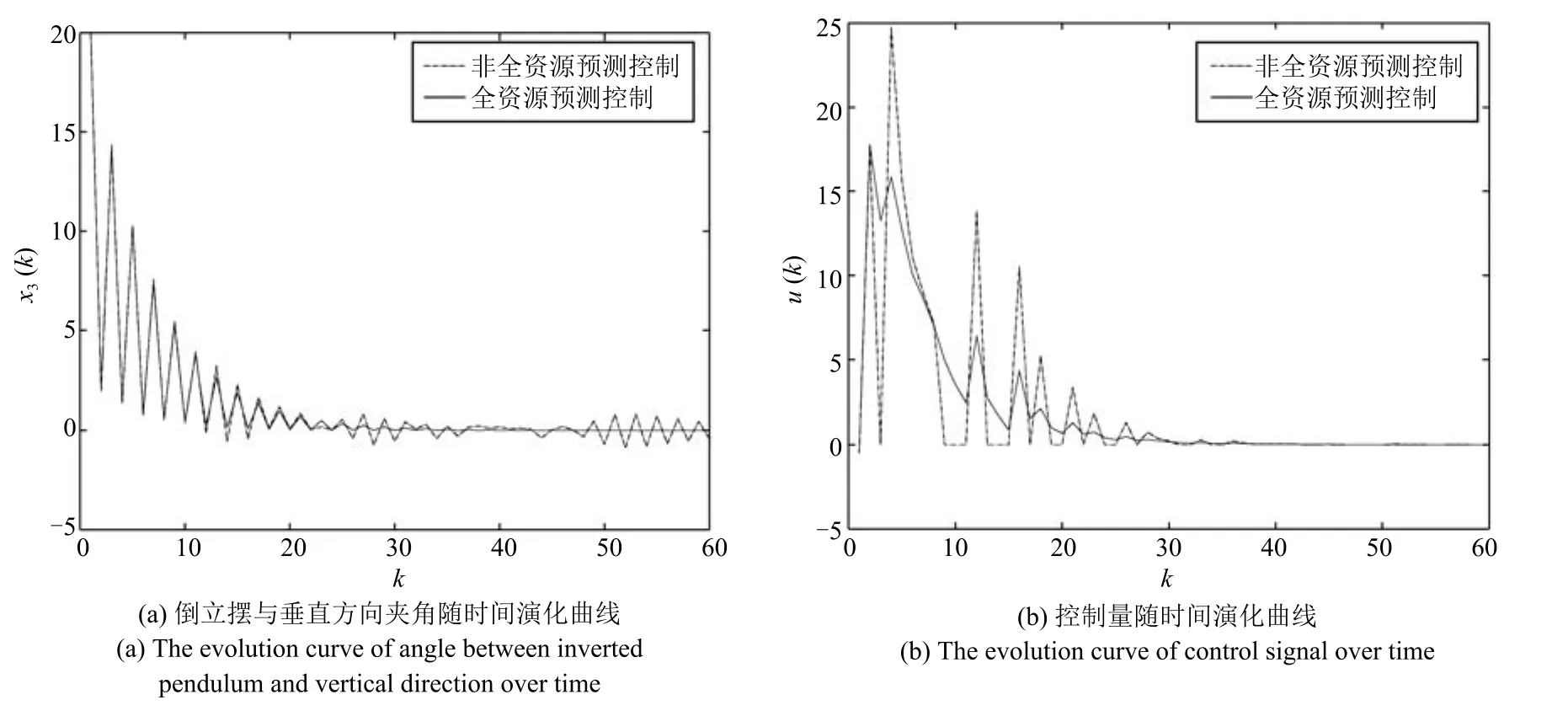
圖5 MATLAB仿真的系統響應和控制量曲線Fig.5 The system responses and control signals in MATLAB simulation
例2.MATLAB/LabVIEW聯合仿真
本例仍考慮圖3中的小車–倒立擺系統,但使用MATLAB/LabVIEW聯合仿真的方法來驗證我們提出的全資源預測控制策略和算法的有效性.系統實現的架構見圖6.其中受控對象即小車–倒立擺系統在LabVIEW中實現,而控制部分則在MATLAB中實現,二者通過LabVIEW中的MATLAB腳本調用實現聯合仿真.LabVIEW 中的小車–倒立擺系統添加了一個很小的外部擾動以模擬真實情況.計算資源的刻畫則以MATLAB的控制器程序運行時間為標準.因此,與僅基于MATLAB的純數值仿真相比,這一聯合仿真方案具有如下優點:1)LabVIEW中實現的小車–倒立擺系統更為真實的模擬了受控對象;2)計算資源的具體定量描述也更為真實,因此可更有效地驗證本文中提出的控制策略和算法.
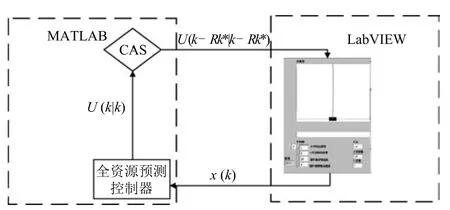
圖6 MATLAB與LabVIEW聯合仿真系統結構Fig.6 The diagram of MATLAB and LabVIEW Co-simulation
控制器執行所需要的計算資源通過MATLAB重復實驗并歸一化,結果如下:
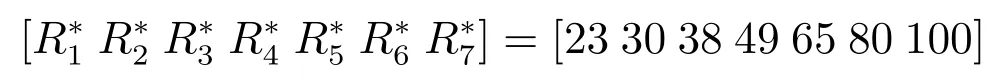
與例1類似,同樣使用兩種方法進行比較,一種使用我們的全資源預測策略,另一種不使用.系統響應證明了全資源預測控制策略可以保證倒立擺在垂直方向的穩定性(圖7(a)),而不使用我們的策略,即便采用同樣的控制器設計,也無法保證倒立擺的穩定性(圖7(b)).
5 結論
通過對可用計算資源的充分利用,在不增加額外計算資源要求的前提下實現了計算受限控制系統的性能提升.這是一種控制和計算的聯合設計方法,對該方法的進一步改進將依賴于前向預測控制序列的更為有效的設計,另外對閉環系統穩定性的保證也是后續的研究工作之一.
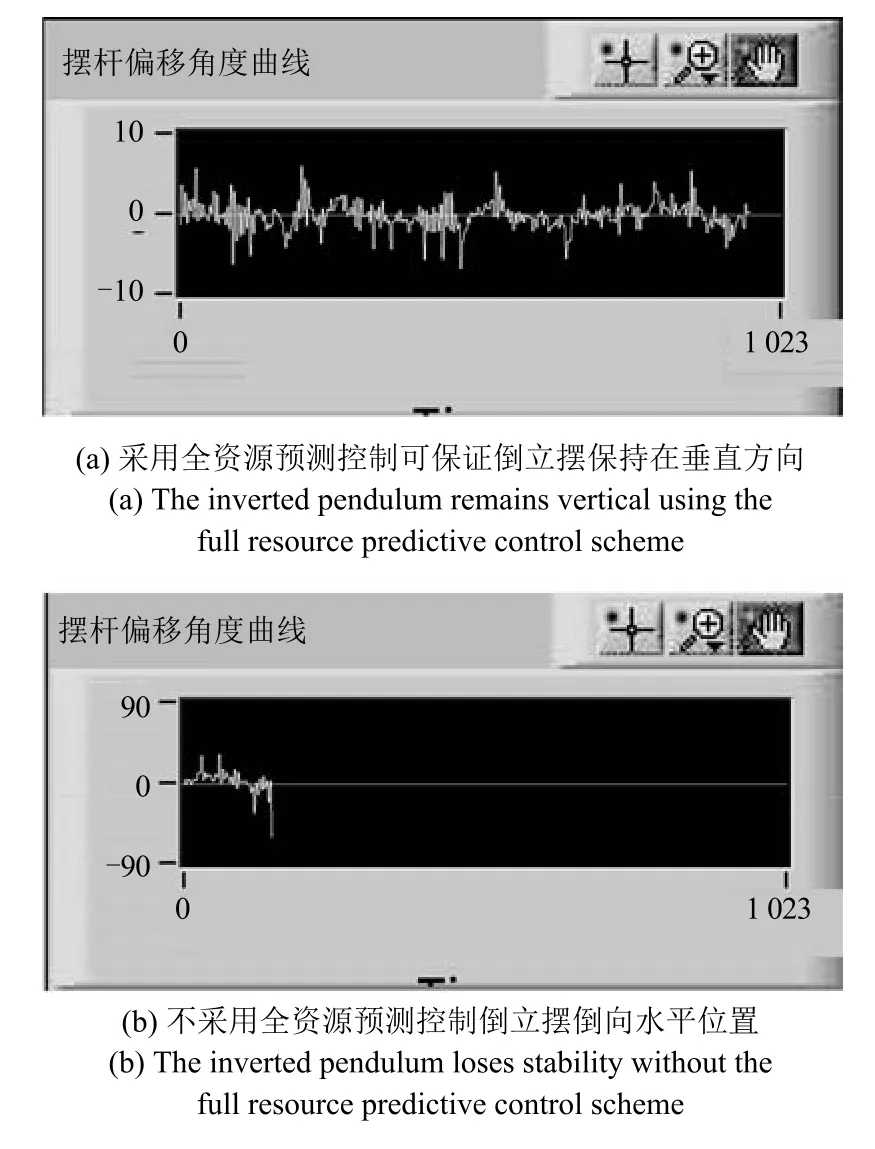
圖7 MATLAB和LabVIEW聯合仿真的系統響應Fig.7 The system responses using MATLAB and LabVIEW co-simulation

