基于ICUOWGA-RBF神經網絡的裝配式建筑施工安全評價

閆帥平，張 杰

(濟源職業技術學院建筑工程系，河南 濟源 459000)

裝配式建筑在提高工程質量、節約資源、保護環境等方面相對于傳統建筑更具有優勢[1]。但是，目前的施工技術和人員素質難以滿足裝配式建筑多維作業空間并行施工的安全要求，極易發生安全事故[2]。2016年國務院辦公廳在《關于大力發展裝配式建筑的指導意見》中指出：“力爭用十年左右的時間，使裝配式建筑占新建建筑面積的比例達到30%”[3]。該政策的實施將我國裝配式建筑產業推向高潮，使得裝配式建筑施工的安全管理面臨重要的挑戰。

目前，國內外學者對裝配式建筑施工安全評價方法進行了大量的研究。在國外，Li等[4]借助系統動力學和Vensim 軟件確定了裝配式建筑施工安全評價指標;Chang等[5]建立了基于層次分析法的裝配式建筑施工安全評價模型，但評價結果存在較大的主觀性。在國內，傳統建筑施工安全評價方法已取得了豐碩的成果[6]，但由于裝配式建筑施工與傳統建筑施工存在較大的差異，導致傳統建筑施工安全評價方法無法直接運用于裝配式建筑施工的安全評價中。裝配式建筑在最近幾年才得到快速發展，目前針對其安全管理的研究較少，現有的裝配式建筑施工安全評價方法主要有事故樹分析法[7]、系統動力學法[8]、層次分析法和熵權法[9]、可拓學理論[10]、G1-物元分析法[11]、系統動力學[12]。但這些評價方法多是借助決策者主觀設定數據的基礎上，未同時考慮評價指標的不確定性、隨機性和指標間非線性關系且計算過程繁瑣，難以滿足裝配式建筑施工安全評價的要求。鑒于此，本文提出了基于ICUOWGA-RBF神經網絡的裝配式建筑施工安全評價方法。該方法先參考安全事故致因理論構建裝配式建筑施工安全評價指標體系；然后引入模糊語義算子對CUOWGA算子進行改進得到評價指標的權重；最后運用RBF神經網絡處理指標的隨機性和指標間的非線性關系，輸出裝配式建筑施工的安全等級。

1 裝配式建筑施工安全評價指標體系的構建

裝配式建筑施工可劃分為構件生產、構件運輸、現場吊裝、構件安裝4個主要過程。與傳統建筑工程相比，裝配式建筑工程具有高空作業多、吊裝難度大、機械化要求高等特點，導致施工不安全因素具有隨機性，且現場存在較大的安全隱患。徐峰等[13]研究認為高處墜落、物體打擊、坍塌、起重機械傷害是傳統建筑施工主要的安全風險因素；文敏等[14]通過對裝配式建筑項目進行實地調研，認為高空臨邊作業、構件吊裝及安裝、觸電、高空墜落、構件裝運卸載是裝配式建筑施工的主要安全風險。本文在傳統建筑施工安全風險因素研究的基礎上，從裝配式建筑施工安全事故成因的角度出發，反推、歸納出“人員-物-管理-技術-環境”5個二級評價指標、27個三級評價指標，構建了裝配式建筑施工安全評價指標體系，具體見表1。

表1 裝配式建筑施工安全評價指標體系

2 基于ICUOWGA-RBF神經網絡的裝配式建筑施工安全評價方法

2.1 評價方法的適用性分析

2.1.1 ICUOWGA算子賦權

常規賦權方法諸如層次分析法、專家調查法、德爾菲法等均是借助專家對指標的認知進行賦值，其結果存在較大的主觀不確定性。CUOWGA算子在一定程度上規避了專家決策過程中的主觀臆斷性，但卻存在主觀條件已定的缺陷，降低了評價結果的科學性[15]。本文在傳統CUOWGA算子的基礎上，引入模糊語義量化算子得到ICUOWGA算子，通過模糊區間數確定專家決策數據，構建規范化矩陣，進而得到評價指標的權重，這在一定程度上規避了專家決策的臆斷性。

2.1.2 RBF神經網絡訓練

裝配式建筑施工安全評價指標間的關系復雜，并非嚴格意義的線性關系。傳統的模糊數學、灰色理論等方法基本上從線性的角度來解決指標間相互作用對目標的影響。RBF神經網絡相對于BP神經網絡在逼近能力、學習和收斂速度方面更勝一籌，可以更好地處理系統內部復雜的規律，被廣泛應用于風險預測、信息處理等領域[16]。因此，本文利用RBF神經網絡訓練樣本數據，以規避模擬過程陷入局部最小值的缺陷。

2.1.3 基于ICUOWGA-RBF神經網絡的裝配式建筑施工安全評價

裝配式建筑施工安全評價是一個動態的變化過程，施工過程需及時根據實際情況做相應調整，若每次評價均需根據ICUOWGA算子求得的指標權重重新計算，將會導致評價過程繁瑣且容易出錯，也使該方法失去了可擴展性。故本文通過ICUOWGA算子與RBF神經網絡結合，利用訓練成熟的網絡充分存儲專家知識和經驗，當進行新的評價時，無需重新訓練網絡結果，只需調整輸入參數，即可得到目標評價值，提高了評價結果的延展性。

2.2 利用ICUOWGA算子計算評價指標的權重

本文引入模糊語義量化算子，通過構建規范化決策矩陣對傳統CUOWGA算子進行改進，進一步消除運算過程的主觀性，具體步驟如下：

(1) 引入模糊語義量化算子：設評價指標權重矩陣w=(w1,w2,…,wk,…,wn),wk=Q(k/n)-Q[(k-1)/n]

(1)

其中Q為模糊語義量化算子，則有：

(2)

式中：模糊語義算子Q(r)為(a,b)=(0.3,0.8)、(a，b)=(0，0.5)、(a，b)=(0.5,1)，分別表示為“大多數”、“至少半數”、“盡可能多”，a,b,r∈[0,1]。

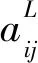
對于成本型指標為

(3)

對于效益指標為

(4)

(3) 構建可能度矩陣P=(pij)m×n：設a=[aL,aU]、b=[bL,bU]，令la=aU-aL、lb=bU-bL，區間數a≤b的可能度定義為

(5)

對規范化矩陣R=(rij)m×n中數據作兩兩比較，得到可能度矩陣P=(pij)m×n。

(4) 構建排序向量：利用下式計算互補判斷矩陣：

(6)

得到排序向量v=(v1,v2,…,vn)T。

(5) 計算評價指標的權重：按照從大到小的順序對向量vi中的aij進行重新排序，得到新的一組數據bj，再運用模糊語義量化評價指標權重矩陣w對數據bj進行加權運算，得到ICUOWGA算子：

(7)

通過利用ICUOWA算子對指標進行歸范化處理得到評價指標的權重。

2.3 RBF神經網絡的樣本訓練

RBF神經網絡作為一種前向反饋型網絡，由輸入層、隱含層、輸出層三部分組成，見圖1。在整個RBF神經網絡訓練過程中需經歷非線性和線性兩

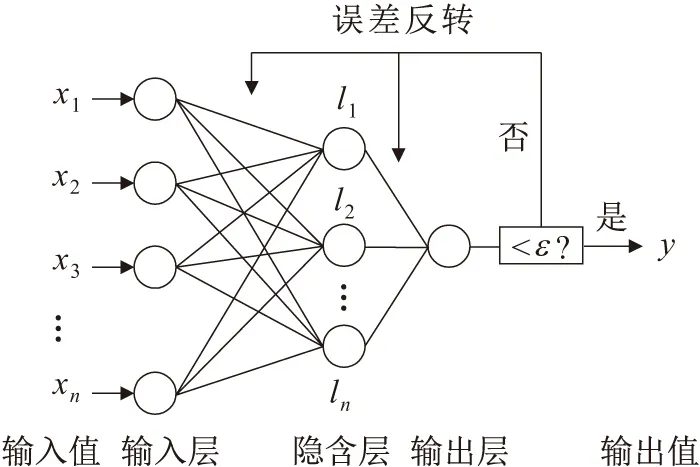
圖1 RBF神經網絡訓練圖Fig.1 RBF neural network training diagram

個階段，其中從輸入層到隱含層為非線性映射，從隱含層到輸出層為線性映射，極好地解決了裝配式建筑施工安全評價指標間復雜的非線性和線性關系。RBF神經網絡理論上可逼近任意函數，通過初始神經逐漸向上迭代，每迭代一次相應增加一個神經元，并尋求最佳權向量，求得目標向量和學習向量的誤差平方和，直到滿足設定誤差時停止訓練，輸出目標評價值。RBF神經網絡的映射關系式為

(8)

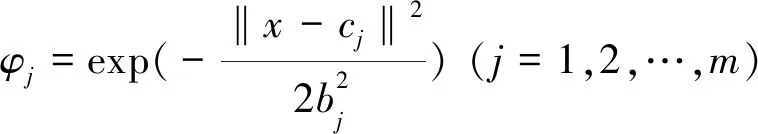
(9)

上式中：x為網絡的輸入樣本數據，x=[x1,x2,…,xn];cj為隱含層j節點奇函數的中心參數，cj=[cj1,cj2,…,cjn]；φj為隱含層神經元j的輸出；b為網絡的寬度向量，b=[b1,b2,…,bm];w為評價指標的權重，w=[w1,w2,…,wm];y為網絡的輸出，y=[y1,y2,…,yn]。

3 案例分析

本文以鄭州某裝配式建筑工程施工項目為例，利用上述建立的基于ICUOWGA-RBF神經網絡的裝配式建筑施工安全評價方法對該項目進行安全評價。

該項目位于鄭州市鴻鵠路與新老107連接線的東北部,規劃用地面積為206 504.7 m2，建筑面積為726 986.6 m2，綠化率為30.20%，容積率為2.7。本文對裝配式建筑施工的安全等級均等劃分，即任何安全等級出現的概率是相同的。借鑒建筑業安全綜合評定等級標準，并結合RBF神經網絡輸出結果，將裝配式建筑施工安全等級劃分為5個級別，分別為高、較高、一般、較低、低，具體詳見表2。

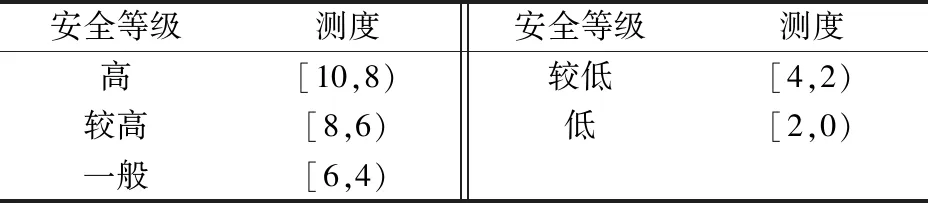
表2 裝配式建筑施工安全等級的劃分

3.1 利用ICUOWGA算子計算評價指標的權重

本文以二級評價指標環境因素A5下5個三級評價指標為例,計算各評價指標的權重，具體計算過程如下：

首先，邀請5位專家參考裝配式建筑施工安全等級劃分范圍對各評價指標進行打分，為了便于計算，所有打分采用5的倍數形式體現，得到專家的初始決策數據，見表3。

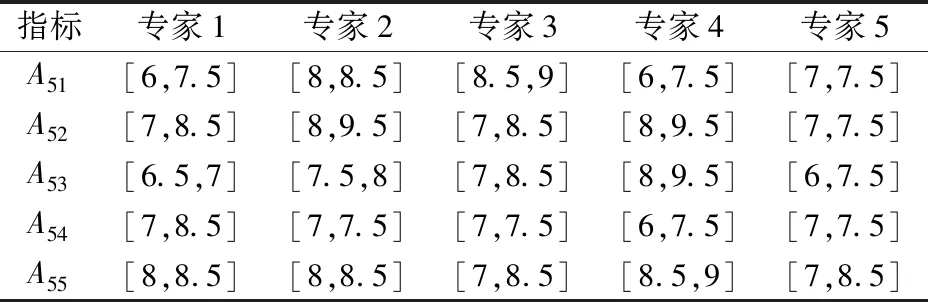
表3 初始決策數據

然后，利用ICUOWGA算子集結處理該初始決策數據，其步驟如下：

(1) 為提升安全等級，默認模糊語義為“盡可能多”，即(a,b)=(0.5，1),參考公式(1)和(2)得到加權向量w=(0.4,0.3,0.2,0.5,0.6)。

(2) 利用公式(3)和(4)對表3初始決策數據進行規范化處理，得到組合決策數據，見表4。

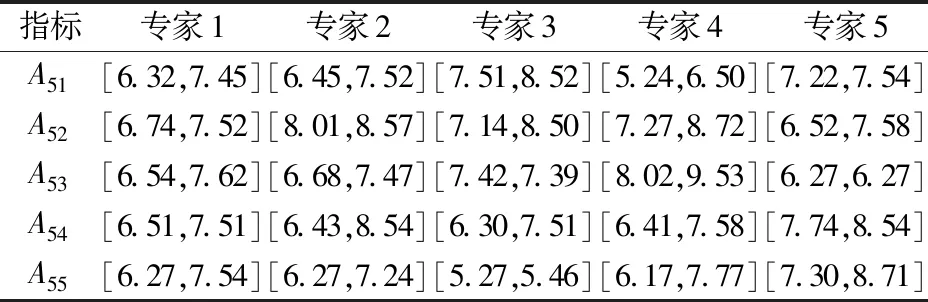
表4 組合決策數據

(3) 根據公式(5)對表4中組合決策數據進行兩兩比較，構建可能度矩陣p(i):

(4) 根據公式(6)求得關于矩陣p的排序向量：

v(1)=(0.447,0.202,0.422,0.427,0.248);

v(2)=(0.175,0.275,0.454,0.277,0.203);

v(3)=(0.374,0.402,0.274,0.237,0.776);

v(4)=(0.472,0.374,0.147,0.278,0.272);

v(5)=(0.447,0.270,0.486,0.236,0.247).

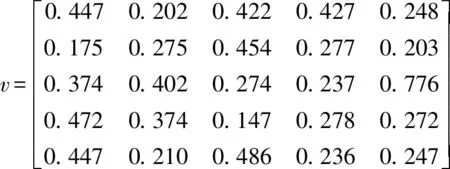
(5) 根據公式(7)求得ICUOWGA51=[3.67,4.25]。為了提升結果的直觀性，取中間數作為評價值，即U51=3.96。同理,求得其他4個三級評價指標ICUOWGA算子的中間數,即U52=3.27，U53=4.16，U54=2.45，U55=2.72。經歸一化后求得5個三級評價指標的權重為：η51=0.239，η52=0.197，η53=0.252，η54=0.148，η55=0.164。

同理，可計算得到其他評價指標的權重為：η11=0.125，η12=0.136，η13=0.201，η14=0.185，η15=0.194，η16=0.159；η21=0.138，η22=0.216，η23=0.197，η24=0.205，η25=0.117，η26=0.127；η31=0.126，η32=0.114，η33=0.233，η34=0.217，η35=0.310；η41=0.173，η42=162，η43=0.236，η44=0.245，η45=0.184；η1=0.348，η2=0.234，η3=0.148，η4=0.137，η5=0.133。

3.2 RBF神經網絡的樣本訓練

3.2.1 RBF神經網絡訓練樣本收集

為提高RBF神經網絡訓練和模擬的能力，參考BP神經網絡對樣本劃分的原則，本文將RBF神經網絡樣本數量按照3∶1∶1的原則分為訓練集、測試集和驗證集三個部分,且所有樣本隨機選擇，以確保輸出結果的科學性。本次訓練共選擇樣本100組，其中訓練樣本60組，測試樣本20組，驗證樣本20組。100組樣本來自河南省10組、浙江省30組、江蘇省20組、深圳市10組、北京市20組、上海市10組，所有數據均來源于當地政府裝配式研究協會和裝配式建筑網。

3.2.2 RBF神經網絡的訓練和測試

本文借助Matlab 2014神經網絡工具包將27個三級評價指標輸入RBF神經網絡，輸出裝配式建筑施工的安全等級。經過多次訓練發現如下規律：訓練次數達到700次，最小訓練速度為0.7，最大允許誤差為0.006，迭代次數為750次，訓練效果最佳，其訓練結果見表5。

由表5可知，學習樣本、驗證樣本的期望輸出值與實際輸出值非常接近，最大絕對誤差值為0.000 5，小于最大允許誤差0.006，表明該模型已達到最佳狀態，可滿足訓練精度的要求，輸出結果可供參考；樣本100的實際輸出值為7.942，參照表2判定該裝配式建筑工程施工項目的安全等級為較高。另外，結合ICUOWGA算子求得的評價指標權重可知，該裝配式建筑工程項目施工過程中應注重對工人專業操作水平、設備定期安全檢驗、構件吊裝安全措施、構件連接節點技術、現場道路情況5個三級指標的安全管理，該結論可為現場的安全管理提供參考。

4 結 論

本文提出了基于ICUOWGA-RBF神經網絡的裝配式建筑施工安全評價方法。該方法通過引入模糊語義量化算子實現了對傳統CUOWGA算子的改進，更加客觀地求得了各評價指標的權重，提高了賦權的科學性；同時利用RBF神經網絡處理小樣本的優勢和同時處理指標間線性和非線性關系的能力，根據訓練成熟的網絡參數，當訓練指標變化時可快速重新得到新的評價結果，提高了評價結果的延展性。實例應用表明：該方法可準確輸出裝配式建筑施工的安全等級，可為裝配式建筑施工日常的安全管理提供重要的參考。