基于自編碼器的飛機類型識別方法

張朝柱，黃妤寧

(哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱150001)

0 引言

非合作通信環境下，通過飛機艙內背景音進行飛機類型的識別[1-2]是目標識別的一個新方向，在軍民用領域有著廣闊的發展與研究前景，對國家安全非常有意義。在非合作通信環境下，利用飛機艙內的背景音信號對飛機類型進行識別具有被動監聽不易被發覺、實時性好、傳播距離遠和實現簡單等優勢，在現實應用中有很大意義。通過截取在非合作通信環境下的飛機艙內的背景音信號對飛機類型進行識別，并且標記出其具體的類型，對軍方迅速識別敵我飛機類型以做出相應的應對措施來說至關重要。將接收到的背景音信號通過計算機進行自主分類與識別，這將大大地解放人力，通過機器代替人類監聽，不僅在準確率上比較穩定，而且對于多重復雜的環境，計算機可以自行進行去除干擾的處理，保證了分類結果的穩定性。文獻[3-5]介紹了MFCC算法對動態環境音進行特征提取，與本文所需要分析的飛機艙背景音有一些相似之處，文獻[6]介紹了支持向量機(SVM)這類傳統的分類算法，但是SVM算法對于本文分析的聲學環境十分復雜的聲信號準確率較低。因此，針對所截取的飛機艙內的背景音，通過MFCC算法進行特征提取，由自編碼器進行分類識別。實驗結果表明，每一類聲信號通過自編碼器可以達到90%以上的正確識別率，且穩定性較高，具有很好的現實意義。

1 自編碼器

自編碼器是一種無監督學習算法，可以對輸入數據進行壓縮，提取其特征進行分類，對圖像信號的分類效果十分顯著。自編碼器[7-9]原理簡單，分類特征明顯且輸出維度低，目前正在多種領域嶄露頭角。本文首次將自編碼器應用于非合作通信環境下飛機背景音聲信號的分類識別，基于自編碼器對多維信號分類更加準確的特點，通過聯合特征對自編碼器進行優化，使其獲得更高的準確率。2010年，Vincent P，Larochelle H，Lajoie I等人提出了一種基于疊加去噪層的深度網絡構建策略自編碼器，其分類錯誤顯著降低，確立了去噪準則可以作為無監督目標來指導更高層次的學習[10-11]。自編碼器是基于深度神經網絡的語音聲學建模、大數據下的模型訓練技術，在未來圖像、語音等大數據處理應用上有著廣闊前景。

1.1 自編碼器原理

自編碼器中，輸入層到隱藏層相當于一個編碼過程，隱藏層到輸出層相當于一個解碼過程，由于在自編碼器中只有無標簽的數據，將輸入信息輸入到編碼器中會得到一個編碼，之后通過解碼器解碼，得到輸出信息[12]。這樣就得到了輸入信號的數據逆向映射特征，也就是從少量樣本和大量無標簽數據中學習到了輸入數據深層次的特征。如果輸出信息和原始輸入信息是相同的，則認為中間隱藏層得到的編碼就是輸入信息的另一種表達方式[13]。通過優化編碼器與解碼器的參數，最小化重構誤差得到編碼。自編碼器的隱藏層到輸出層為前饋運算，其隱藏層可以完整地表達該輸入信號，即可以從隱藏層中將輸入信號進行無損重構，即自編碼[14]。傳統的自編碼器主要用于降維或者特征學習，其原理結構如圖1所示。

圖1 自編碼器原理結構

自編碼器的訓練近似于受限玻爾茲曼機，訓練一個自編碼器是為了把輸入x編碼為某種表示c(x)，以便于輸入可以從這種表示中進行重構，如果存在一個線性隱藏層，并且采用均方誤差準則訓練這個網絡，那么k個隱藏單元學習到的就是將輸入向量投影到由數據空間的前k個主成分所張成的子空間[15]。如果隱藏層是非線性的，那么自編碼器便與主成分分析PCA不同：它將有能力捕獲輸入分布的多模特性。更理想的情況下，可以把均方誤差準則推廣到重構的最大似然準則，即負對數似然的最小化準則。

1.2 自編碼器的訓練

給定編碼c(x)：

RE=-lgP(x|c(x))。

(1)

如果x|c(x)為分布式高斯的函數，式(1)可表示均方誤差，若輸入xi是一個二元變量或者近似二項分布的函數，則其代價函數為：

(1-xi)lg(1-fi(c(x)))。

(2)

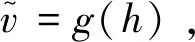
(3)

理論上來說，確定的函數編碼f(v)以及確定的解碼函數g(h)可以是任意函數。使用自編碼器來初始化由signmoid單元構成的DNN中的權重時，

h=f(v)=σ(Weh+b)，

(4)

式中，We∈RNh×Nv是編碼矩陣；b∈RNh×1是隱藏層的偏置向量。如果輸入特征v∈{0，1}Nv×1取二進制值，則可以選擇

(5)

式中，a∈RNv×1是重建層偏置向量。如果輸入特征v∈RNv×1取實數值，可以選擇：

(6)

一般情況下，權重矩陣we和wd可能是不相同的。反向傳播算法可以學習自編碼器中的任何類型任何方式的參數，包括實數或者二進制數等。

當隱藏層h的維度比輸入信號x小時，將強制自編碼器捕捉訓練數據中最顯著的特征。其訓練函數為：

L(x，g(f(x)))，

(7)

式中，L是損失函數，將其最小化可用于懲罰函數g(f(x))與x的差異，如均方誤差或者交叉熵損失函數，二者分別表示為：

L(x，y)=‖x-y‖2，

(8)

(9)

1.3 自編碼器的輸出

假設某輸入樣本i對應的向量為x(i)，那么其隱含層中的響應向量為：

a(i)=f(z(i))=f(Wx(i)+b1)，

(10)

式中，W是輸入層的權重矩陣；b1是輸入層的偏置矢量；z(i)是計算隱藏層求和；f(?)是激活函數，且在此情形下應該是一個值域在(0，1)之間的向量。本文選取sigmoid激活函數。可知在sigmoid激活函數下，自編碼器的輸出為：

(11)

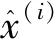
2 MFCC算法提取飛機聲信號特征

本文對8種不同飛機類型通過MFCC對原始聲信號進行特征提取，得到特征向量。

Mel頻率分析是一種仿人耳的頻率分析。由于人耳對聲音的非線性關系，通過Mel倒譜將線性頻譜通過某種關系映射到非線性頻譜中，通過倒譜將其線性卷積關系變成線性相加關系[16]。Mel頻率與實際頻率的關系如圖2所示，其變換關系式為：

(12)

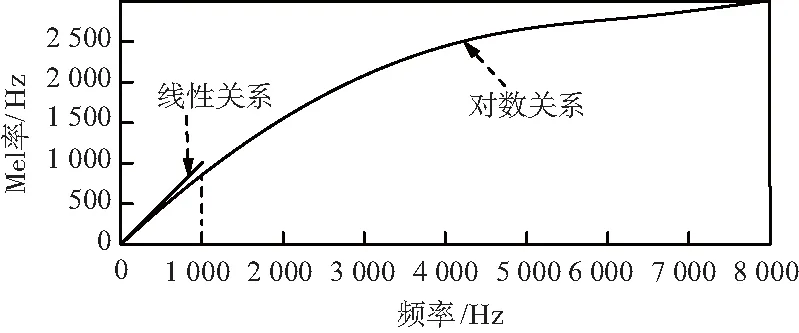
圖2 Mel頻率與線性頻率關系

在Mel頻域，人耳的頻率分辨率是均勻分布的，即將整個Mel頻域等距劃分得到若干個中心頻率。以每個中心點為中點，將上一個和下一個中心頻率為截止頻率，構建一系列三角帶通濾波器，并通過式(12)計算Mel頻率與實際頻率的對應關系[17]。MFCC算法流程為：預加重、分幀、加窗、傅里葉變換、三角窗濾波、取對數、離散余弦變換(DCT)和動態差分。

圖3 MFCC算法流程

① 預加重。可以提高聲信號的高頻部分，將聲信號通過一個高通濾波器使能量譜更加均衡。

② 分幀。根據短時平穩特性將聲信號進行分幀。每一幀中包含N個采樣點，為了避免丟失語音信號的動態變化信息，相鄰2幀之間的分幀會進行一部分的重疊。

③ 加窗。增加相鄰幀之間的左右連續性。通常情況下，實驗使用邊緣平滑降為零的漢明窗。

④ 傅里葉變換。將預處理后的語音信號進行離散傅里葉變換，得到信號的線性頻譜，將信號進行時頻轉換，這就可以對頻域信號取模平方計算其功率譜。設加窗后的信號為x(n)，經過離散傅里葉變換后：

X(K)=DFTx(n)，

(13)

X(K)=H(K)E(K)，

(14)

x(n)=h(n)*e(n)。

(15)

⑤ 三角窗濾波。將經過傅里葉變換后得到的頻域信號輸入到Mel濾波器中使其變成Mel頻譜，就可這樣根據式(12)得到實際頻率與Mel頻率的轉換關系。

⑥ 取對數能量。將時域卷積轉化為頻域相加，

lgX(k)=lg(H(K))+lg(E(K))。

(16)

⑦ 倒譜。即為離散余弦變換，將頻域相加的關系轉化成時域相加的關系，找到信號的另外一種表示。倒譜能夠去除幀內和幀間的冗余信息，且倒譜系數之間不具有相關關系[17]：

IDFT[lgX(K)]=IDFT[lg(H(K))+

lg(E(K))]，

(17)

(18)

⑧ 差分。由于語音信號為時域連續信號，標準的MFCC只能表示信號的靜態特征，即一幀內的語音特征，將靜態特征求解一階差分和二階差分得到其動態特征信息，使特征更加連續，下一步的分類識別的準確率會更高。

原始的聲信號數據進行MFCC算法提取特征值，得到8類數據24維的MFCC特征向量，其中采樣間隔20 ms，每幀間重疊10 ms，將特征向量輸入自編碼器進行分類。

3 自編碼器對飛機聲信號特征分類

針對飛機聲信號特征值進行自編碼器分類，輸入聲信號經過自編碼器的編碼解碼完成了一種降維的輸入輸出同維度計算過程，解碼后，由Softmax進行分類，得到8類不同的聲信號分類結果。自編碼器分類原理如圖4所示。

圖4 自編碼器分類原理

輸入為24維MFCC特征信號，由于自編碼器的降維分類特征，8類聲信號特征準確率的穩定性存在一定差異。在MFCC算法下，自編碼器可以分類出8種不同的飛機類型，但是自編碼器對于本文類別1號聲信號的分類準確率較其他信號相對準確率低，針對這一問題，提出了基于小波包分解[18]—MFCC聯合特征，通過自編碼器進行聯合特征提取分類，將原始聲信號通過小波包分解得到8維小波包重構特征信號，與MFCC算法提取的24維特征信號組合成32維聯合特征，輸入自編碼器進行分類。

4 實驗結果對比分析

對原始聲信號進行MFCC算法特征提取，采樣頻率選取20 ms一幀，10 ms一次重疊，自編碼器的隱含層節點設為10；將MFCC提取的特征向量輸入自編碼器，并且通過10次重復實驗來驗證準確率誤差情況，得到10次重復實驗分類準確率如圖5所示。

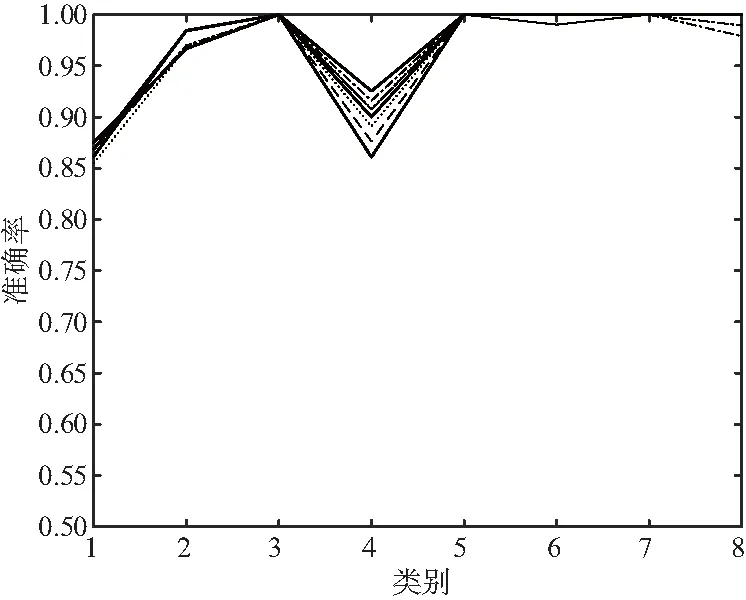
圖5 MFCC算法下自編碼器10次實驗分類準確率

根據多次重復實驗的準確率統計平均值，可以得到每一類聲信號的近似分類準確率，如表1所示。其中，為了獲得穩定的統計平均值，取重復實驗次數為100次。

表1 MFCC算法下自編碼器100次分類準確率平均值

信號12345678準確率/%86.2397.13100.0090.12100.0099.90100.0099.68

圖5中，橫坐標為重復實驗次數，縱坐標為每一次實驗準確率，折線為每一種聲信號的類型。由圖5以及表1可以看出，在MFCC算法下，每一類聲信號的自編碼器的分類準確率均在85%以上，平均準確率為95.98%，除了類別1的86.23%，其余準確率均在90%以上。實驗證明，在MFCC算法下，自編碼器可以較為準確地分類出8種不同的飛機類型。

對于類別1聲信號識別準確率較其他信號低的問題，將32維聯合特征作為輸入特征信號，經過自編碼器分類的結果如表2所示，其中準確率均取100次重復實驗后10次的平均值。

表2 聯合特征算法下自編碼器分類準確率 %

由表2可以看出，聯合特征提取通過自編碼器進行分類，其類別1信號由原來MFCC算法下的86.23%增加為99.91%，且MFCC算法下，類別4的分類結果比起其他類別聲信號較低，經過聯合特征進行提取后，其準確率由90.12%提高到92.46%，其他類別信號也有小幅度的提升，多次重復實驗結果波動較小，說明對于實際信號應用中相對穩定。相比于MFCC算法下的分類結果，整體的平均正確率從95.98%提升至97.74%，實驗結果證明其整體正確率提升效果明顯且分類結果穩定。

5 結束語

針對截取的非合作通信環境下飛機駕駛艙內的聲信號，提取非語音段聲信號的特征值，提出了對提取特征通過自編碼器值進行分類來準確判斷飛機類型。本文是將8類不同類型的飛機通過截取背景音信號進行特征提取和分類；背景音的聲信號主要位于低頻段且為非線性時變信號，根據聲信號的短時平穩性應用MFCC算法對8種不同飛機的聲信號進行特征提取，將自編碼器首次應用于本文研究的聲信號特征分析中進行分類，經過MFCC算法特征提取后的自編碼器對8類信號100次重復實驗的平均準確率分別為：86.23%，97.13%，100.00%，90.12%，100.00%，99.90%，100.00%，99.68%。針對自編碼器對類別1的準確率較其他信號低的問題，提出特征聯合—自編碼器對自編碼器進行優化。實驗結果表明，優化自編碼器的類別1聲信號的平均準確率為99.91%，準確率較未優化的自編碼器提高了13.68%。另外，本文研究的聲信號聲學環境復雜，可能存在更好的特征提取方法以待研究，目前97.74%的平均準確率已經可以在實際應用中發揮較好的應用效果。