融合高斯過程回歸的UKF估計(jì)方法

葉文，蔡晨光，楊平，李建利

（1.中國計(jì)量科學(xué)研究院 力學(xué)與聲學(xué)計(jì)量科學(xué)研究所，北京100029；2.北京航空航天大學(xué) 儀器科學(xué)與光電工程學(xué)院，北京100083）

高精度位置姿態(tài)測量系統(tǒng)（Position and Orientation System，POS）本質(zhì)是一個(gè) SINS／GNSS非線性組合系統(tǒng)，其通過非線性濾波方法，如擴(kuò)展卡爾曼濾波（Extended Kalman Filter，EKF）、無跡卡爾曼濾波（Unscented Kalman Filter，UKF），融合來自GNSS和SINS的位置、速度等運(yùn)動參數(shù)，估計(jì)SINS的狀態(tài)誤差，進(jìn)而為載荷提供可靠、高頻、高精度的運(yùn)動信息[1-2]。無論是線性濾波還是非線性濾波，都需要事先精確建立慣導(dǎo)誤差模型和確定噪聲統(tǒng)計(jì)特性[3-4]。然而，這存在 2個(gè)嚴(yán)重問題：①精確建立誤差模型幾乎不可能，因?yàn)橄到y(tǒng)復(fù)雜時(shí)變；②已知噪聲統(tǒng)計(jì)特性會隨著系統(tǒng)的工作狀態(tài)變化而變化。眾所周知，由于后處理平滑利用了所有可觀測的信息，理論上其具有最高的估計(jì)精度[5-6]。因此，一方面，后處理平滑結(jié)果可作為基準(zhǔn)數(shù)據(jù)；另一方面，濾波估計(jì)方法仍有提升的空間。然而，怎樣提升濾波估計(jì)精度是一個(gè)很有挑戰(zhàn)的難題。

隨著機(jī)器學(xué)習(xí)的發(fā)展，該問題得以解決。尤其是以高斯過程回歸（Gaussian Process Regression，GPR）為主的無參數(shù)回歸方法，具有不確定度輸出、非線性映射、隨機(jī)性預(yù)測等優(yōu)點(diǎn)，很適合與貝葉斯濾波方法進(jìn)行結(jié)合[7-11]。因此，針對UKF不可能把系統(tǒng)的所有誤差源都考慮到，導(dǎo)致UKF的預(yù)測和估計(jì)能力仍有局限性的問題，本文提出了一種增強(qiáng)高斯過程的UKF（Enhanced GPUKF，EGP-UKF）方法。該方法的核心思想是利用GP學(xué)習(xí)濾波估計(jì)值與后處理平滑估計(jì)值之間的殘差。

本文詳細(xì)論述了如何使用非參數(shù)GP學(xué)習(xí)狀態(tài)模型和量測模型與真實(shí)值（平滑）之間的殘差，以及如何無縫地把這些殘差融合到UKF中。由此產(chǎn)生的EGP-UKF方法具有非參數(shù)GP的優(yōu)點(diǎn)：①EGP-UKF方法取決于已建立的狀態(tài)模型和量測模型，但不需要完全精確的數(shù)學(xué)模型，而且也取決于GP模型，EGP-UKF模型及其參數(shù)可以從較少的訓(xùn)練數(shù)據(jù)中學(xué)習(xí)得到；②EGP-UKF方法考慮了動態(tài)模型的不確定性。此外，UKF可避免因沒有足夠的訓(xùn)練數(shù)據(jù)引起的EGP-UKF更多不確定性。通過車載實(shí)驗(yàn)驗(yàn)證了EGP-UKF方法的估計(jì)性能，實(shí)驗(yàn)結(jié)果表明，該方法可明顯提高 POS的濾波估計(jì)精度。

1 SINS／GNSS組合導(dǎo)航

1.1 非線性慣導(dǎo)誤差模型及狀態(tài)方程

本文采用基于角誤差模型的非線性姿態(tài)誤差方程，該非線性誤差模型是UKF的基礎(chǔ)。首先定義坐標(biāo)系，i為慣性坐標(biāo)系，p為平臺坐標(biāo)系，n為導(dǎo)航坐標(biāo)系，b為載體坐標(biāo)系，e為地球坐標(biāo)系。

1.1.1 姿態(tài)誤差微分方程

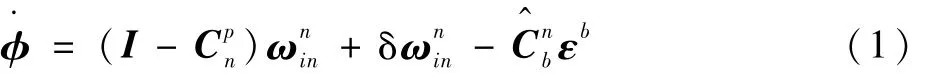
式中：φ=[φEφNφU]T描述數(shù)學(xué)平臺坐標(biāo)系與導(dǎo)航坐標(biāo)系之間的失準(zhǔn)角；Cpn為平臺坐標(biāo)系p到導(dǎo)航坐標(biāo)系n的方向余弦矩陣；ωnin為投影在導(dǎo)航坐標(biāo)系n下的導(dǎo)航坐標(biāo)系n相對于慣性坐標(biāo)系i的角速度；δωnin為其誤差；εb=[εxεyεz]T為陀螺儀隨機(jī)漂移在載體坐標(biāo)系b的投影；為從載體坐標(biāo)系b到導(dǎo)航坐標(biāo)系n方向余弦陣Cnb的估計(jì)；（I-Cpn）ωnin為姿態(tài)誤差微分方程中的非線性部分。

1.1.2 速度誤差微分方程

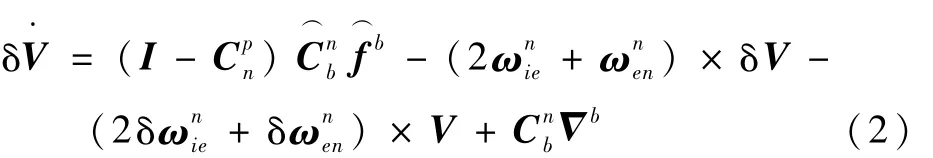
式中：V=[VEVNVU]T為導(dǎo)航坐標(biāo)系 n投影下的速度；δV為其誤差為加速度計(jì)所測比力在載體坐標(biāo)系b上的投影；為加速度計(jì)隨機(jī)偏置誤差在載體坐標(biāo)系b下的投影為速度誤差微分方程中的非線性項(xiàng)。

1.1.3 位置誤差微分方程

式中：δL、δλ和 δH分別為緯度、經(jīng)度和高度誤差；RN和 RM分別為橢球卯酉圈和子午圈曲率半徑。

1.1.4 慣性器件方程

慣性測量單元由3個(gè)陀螺儀和3個(gè)加速度計(jì)組Δ成。假設(shè)陀螺儀隨機(jī)Δ誤差ε和加速度計(jì)隨機(jī)Δ誤差 包括隨機(jī)常數(shù) εc、c和高斯白噪聲 εg、g。雖然隨機(jī)常值每次啟動不同，但啟動后是確定的。因此，陀螺儀和加速度計(jì)的隨機(jī)誤差如下：

SINS／GNSS組合導(dǎo)航系統(tǒng)的狀態(tài)方程可以通過誤差模型（包括姿態(tài)誤差、速度誤差、位置誤差、慣性器件陀螺儀和加速度計(jì)的誤差）獲得，其對應(yīng)的狀態(tài)方程為式（1）～式（3）和式（5）。

1.2 量測方程

量測方程是一個(gè)離散的線性方程，通過SINS捷聯(lián)解算的速度／位置和 GNSS的速度／位置差得到。

式中：xk為 POS的狀態(tài)向量；VGE、VGN和 VGU分別為 GNSS的東向、北向和天向速度；LGNSS、λGNSS和HGNSS分別為GNSS測量所得的緯度、經(jīng)度和高度；ZV（k）和HV分別為速度量測信息和速度量測矩陣；ZP（k）和HP分別為位置量測信息和位置量測矩陣；MV和NP分別為GNSS的速度和位置噪聲。

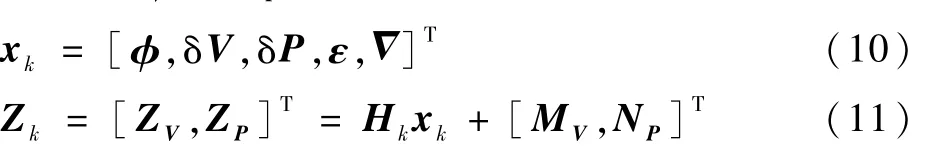
1.3 UKF方法

UKF是Sigma點(diǎn)卡爾曼濾波的一種，通過UT非線性變換逼近非線性系統(tǒng)狀態(tài)的后驗(yàn)均值和協(xié)方差，估計(jì)精度至少能達(dá)到二階泰勒以上，且不需要計(jì)算雅可比矩陣。

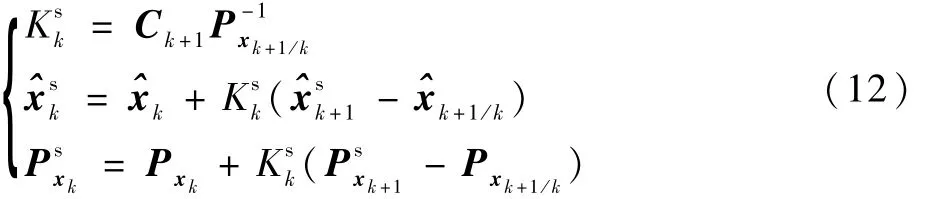
2 高斯過程

GP是一組隨機(jī)變量的集合，且集合中任意數(shù)量的隨機(jī)變量都應(yīng)滿足聯(lián)合高斯分布的隨機(jī)過程，由均值函數(shù)和協(xié)方差函數(shù)確定[12-13]。

式中：xi，xj∈Rd為任意隨機(jī)變量。

式中：xi為輸入量，yi為輸出量，它們分別組成了Xin和為均值為零的高斯白噪聲。

訓(xùn)練集中的Yout和測試點(diǎn)x*的預(yù)測值y*的聯(lián)合分布為

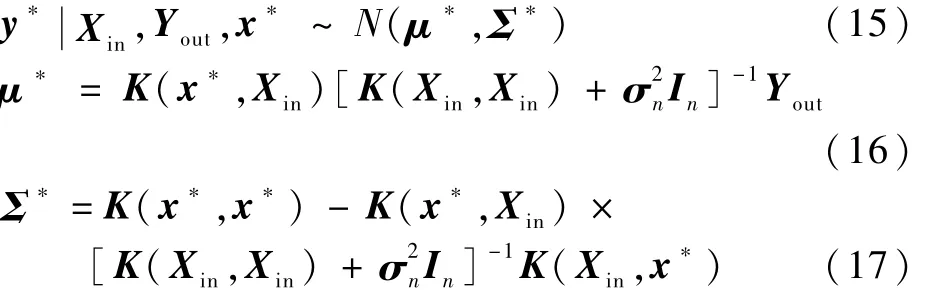
式中：K（Xin，Xin）為對稱的協(xié)方差矩陣；σn為 n維高斯噪聲矩陣；In為n維單位矩陣；μ*為均值；Σ*為方差。

為了實(shí)現(xiàn)最優(yōu)的訓(xùn)練效果，通常采用高斯核函數(shù)，如下：

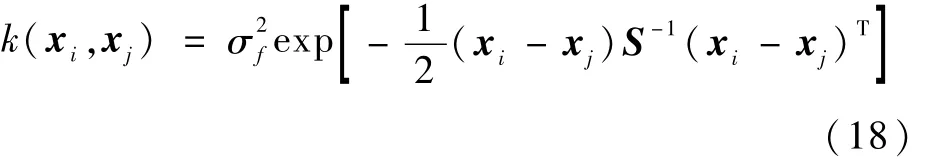
式中：θ=｛S，σ2f，σ2n｝為超參數(shù)，可通過對數(shù)極大似然函數(shù)求解后驗(yàn)分布獲得；σ2f為信號方差。一般采用共軛梯度方法求解最優(yōu)超參數(shù)。函數(shù)的偏導(dǎo)數(shù)如下：

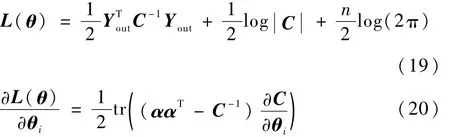
式中：C=K（Xin，Xin）+σ2nIn；α=（K（Xin，Xin）+σ2nIn）-1Yout。

3 EGP-UKF模型

3.1 學(xué)習(xí)狀態(tài)方程和量測方程

EGP-UKF是一種融合數(shù)學(xué)模型和數(shù)據(jù)模型各自優(yōu)勢的高精度濾波模型。利用GP學(xué)習(xí)UKF的狀態(tài)方程和量測方程以及協(xié)方差陣Q和R。針對多維誤差模型，采用 GP學(xué)習(xí)UKF中的每一個(gè)狀態(tài)估計(jì)值和真值之間的差值，且每個(gè)GP的訓(xùn)練數(shù)據(jù)都是一組輸入輸出關(guān)系。采用GP學(xué)習(xí)狀態(tài)模型的殘差時(shí)，首先求解UKF濾波估計(jì)值和后處理平滑值；然后將狀態(tài)模型中當(dāng)前時(shí)刻的狀態(tài)映射到狀態(tài)變化量。量測模型由狀態(tài)映射到觀測，它們分別是由SINS／GNSS組合導(dǎo)航系統(tǒng)后處理平滑和差分GNSS計(jì)算得到的。狀態(tài)模型和量測模型的訓(xùn)練數(shù)據(jù)集的形式分別表示為

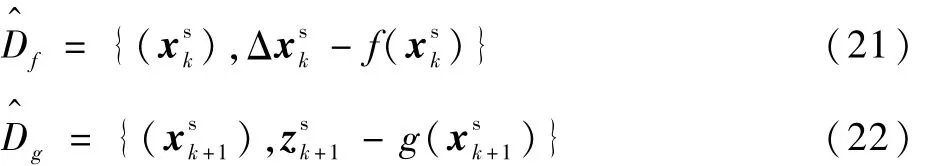
式中：xsk+1為后處理平滑估計(jì)狀態(tài)量；zsk+1為捷聯(lián)

慣導(dǎo)解算結(jié)果和差分GNSS之差。采用GP學(xué)習(xí)狀態(tài)模型和量測模型殘差的數(shù)學(xué)模型如下：

3.2 EGP-UKF方法流程

經(jīng)過上述分析，EGP-UKF方法由2個(gè)階段組成：學(xué)習(xí)和估計(jì)。在學(xué)習(xí)殘差模型階段中，采用GP分別進(jìn)行學(xué)習(xí)狀態(tài)模型和量測模型的訓(xùn)練數(shù)據(jù)），可分別得到狀態(tài)模型和量測模型的殘差回歸模型及其協(xié)方差陣；在估計(jì)殘差模型階段中，在UKF算法的基礎(chǔ)上，采用GP分別對狀態(tài)方程和量測方程的殘差進(jìn)行預(yù)測，并自適應(yīng)獲取其協(xié)方差陣。具體算法如下。

1）初始化

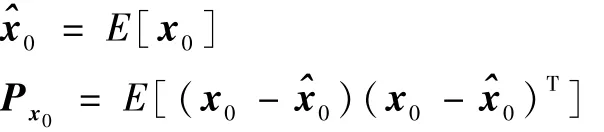
2）計(jì)算 Sigma點(diǎn)

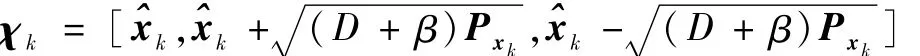
3）時(shí)間更新

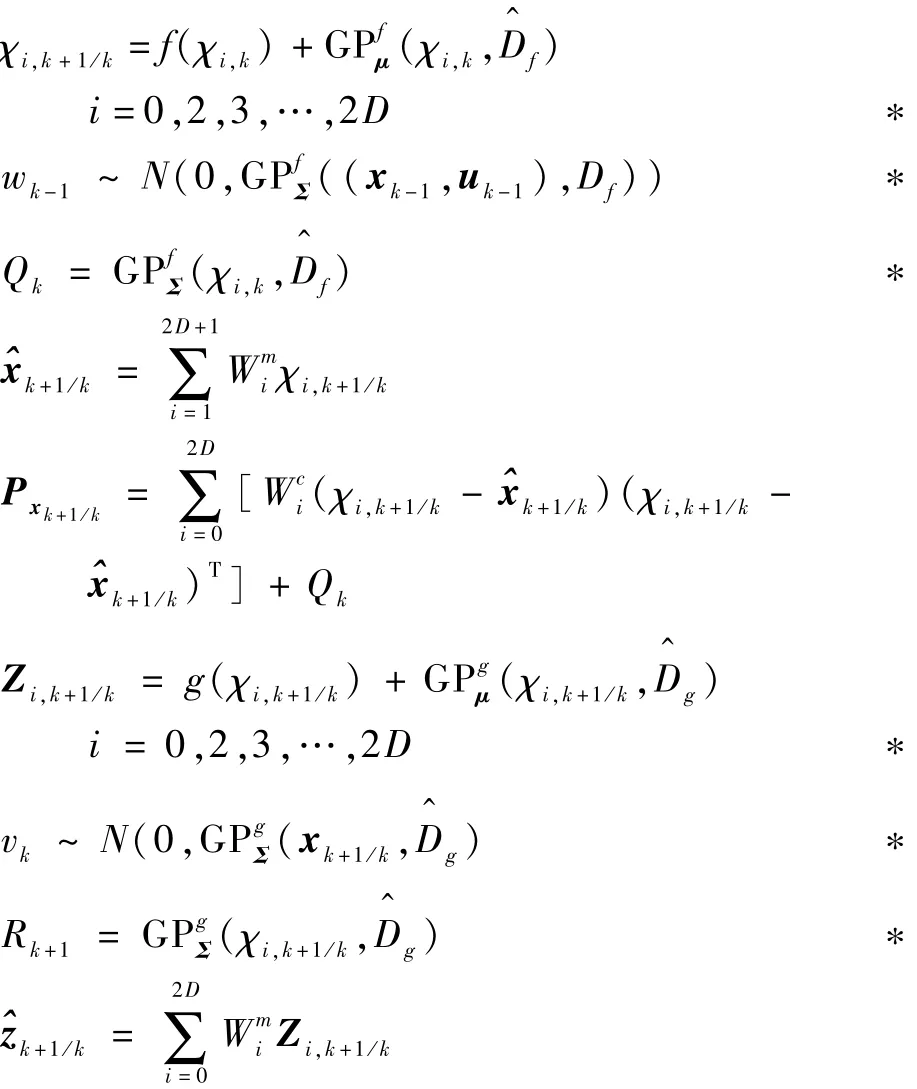
4）量測更新

5）狀態(tài)更新

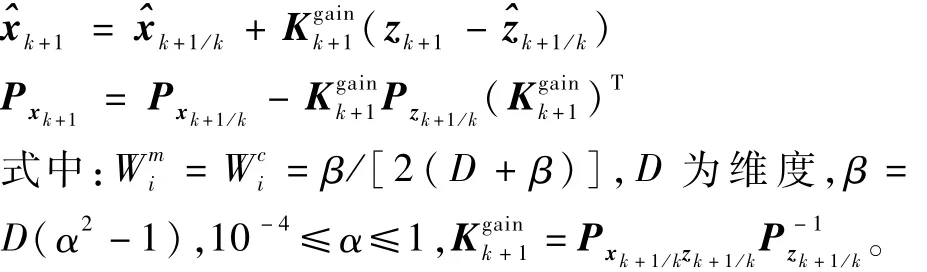
本文提出的EGP-UKF高精度濾波估計(jì)方法不僅不需要訓(xùn)練數(shù)據(jù)包含整個(gè)誤差狀態(tài)空間，也不需要精確的數(shù)學(xué)模型。正如算法中標(biāo)注“*”的公式所示。EGP-UKF建模可以用來學(xué)習(xí)狀態(tài)模型和量測模型，其優(yōu)于參數(shù)模型，特別是當(dāng)參數(shù)模型是不準(zhǔn)確的。GP的殘差模型由GPf和GPg組成，一旦模型被訓(xùn)練好，預(yù)測模型便可得出：

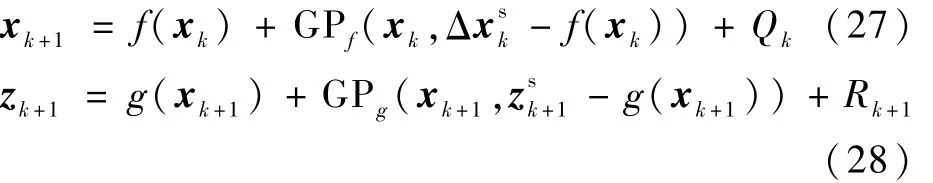
4 車載實(shí)驗(yàn)

為了評價(jià)本文EGP-UKF方法的性能，通過車載實(shí)驗(yàn)數(shù)據(jù)驗(yàn)證了UKF、GP-UKF和EGP-UKF的性能。車載所用的 SINS／GNSS組合導(dǎo)航系統(tǒng)是北京航空航天大學(xué)設(shè)計(jì)的 POS，其由 IMU、GNSS和PCS組成，如圖1所示。此外，為了保證后處理平滑的精度，在實(shí)驗(yàn)過程中架設(shè)了GNSS地面基準(zhǔn)站，如圖1（c）所示。POS安裝在實(shí)驗(yàn)車上，如圖 1（b）所示。

為了保證后處理的精度且更好地評價(jià)EGPUKF的性能，在北京市昌平區(qū)的航空博物館前進(jìn)行了車載實(shí)驗(yàn)。原因如下：①面積開闊，無GNSS信號遮擋；②道路相對平直，約3 km長。在實(shí)驗(yàn)過程中，SINS／GNSS組合導(dǎo)航系統(tǒng)運(yùn)行良好，采集所有相關(guān)數(shù)據(jù)，如IMU數(shù)據(jù)、GNSS數(shù)據(jù)和實(shí)時(shí)組合導(dǎo)航數(shù)據(jù)，時(shí)長約為2200 s。因此，IMU數(shù)據(jù)和差分GNSS數(shù)據(jù)的平滑結(jié)果可以作為真值，其中前 800 s用來訓(xùn)練 GP-UKF[14-15]和 EGP-UKF，最后1 400 s評價(jià)本文方法的性能。車載實(shí)驗(yàn)軌跡如圖 1（d）所示。

圖1 車載實(shí)驗(yàn)Fig.1 Vehicle-mounted experiment

圖2～圖 4給出了 EGP-UKF、UKF、GP-UKF在緯度誤差、經(jīng)度誤差和高度誤差上的對比結(jié)果。在圖2～圖4中，本文提出的EGP-UKF方法和另外2種方法在開始階段的性能幾乎相同，一方面，因?yàn)樵陟o止部分參數(shù)模型與后處理平滑模型基本一致，另一方面在靜止部分本文方法的噪聲幾乎和參數(shù)模型一致。如果發(fā)生了機(jī)動，EGP-UKF精度明顯高于 UKF和 GP-UKF。因?yàn)?EGP-UKF不僅能自適應(yīng)調(diào)節(jié)系統(tǒng)噪聲和量測噪聲，而且還考慮了模型不確定性，然而UKF未考慮模型不確定性和噪聲的影響。盡管GP-UKF考慮了噪聲的影響，但該方法嚴(yán)重依賴數(shù)據(jù)模型，未考慮系統(tǒng)本身的數(shù)學(xué)模型。機(jī)動之后，本文方法也明顯優(yōu)于其他2種方法，因?yàn)镋GP-UKF在系統(tǒng)誤差模型的基礎(chǔ)上進(jìn)一步利用了數(shù)據(jù)模型，抑制了系統(tǒng)誤差模型不確定度的影響。事實(shí)上，模型的不確定主要由參數(shù)模型和相應(yīng)的平滑之間的殘差組成。在某種程度上，EGP-UKF可以學(xué)習(xí)和預(yù)測這種模型不確定性帶來的殘差，并減輕其帶來的不利影響。

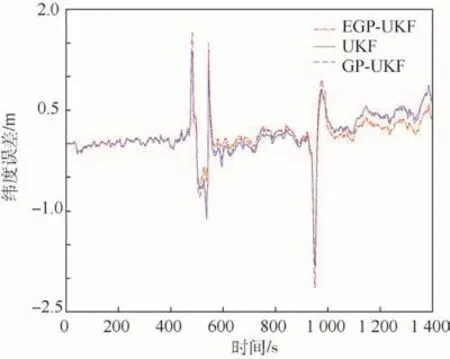
圖2 緯度誤差對比Fig.2 Comparison of latitude error

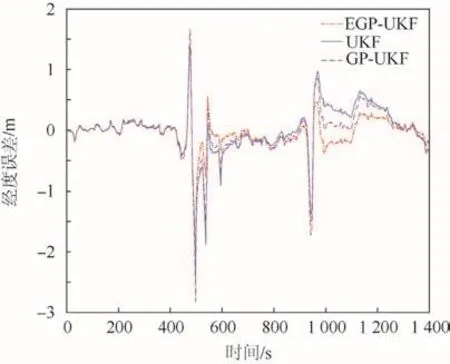
圖3 經(jīng)度誤差對比Fig.3 Comparison of longitude error

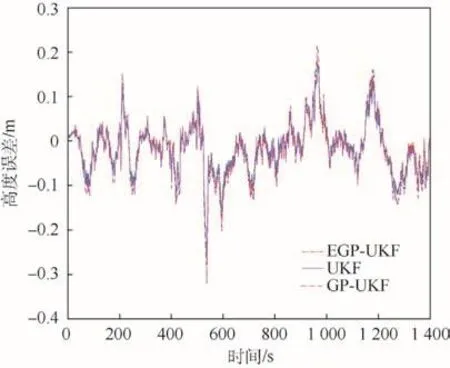
圖4 高度誤差對比Fig.4 Comparison of altitude error

圖5～圖7表明，在東向速度誤差和北向速度誤差方面，EGP-UKF比UKF和GP-UKF的精度更高、更穩(wěn)定。一方面，東向速度誤差在圖3所示經(jīng)度誤差一致；另一方面，北向速度誤差變化和圖2所示的緯度誤差變化一致，符合慣性導(dǎo)航系統(tǒng)的誤差傳播定律。由圖4和圖7可知，高度誤差和天向速度誤差幾乎相同。

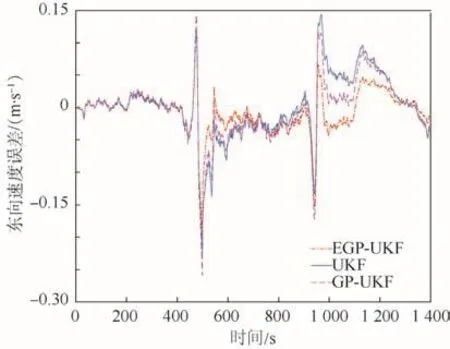
圖5 東向速度誤差對比Fig.5 Comparison of east velocity error

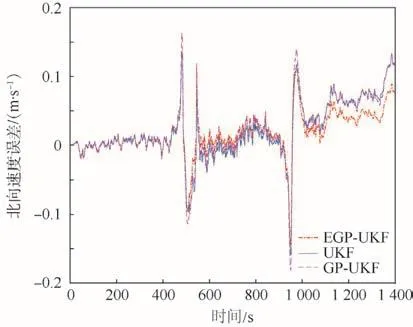
圖6 北向速度誤差對比Fig.6 Comparison of north velocity error

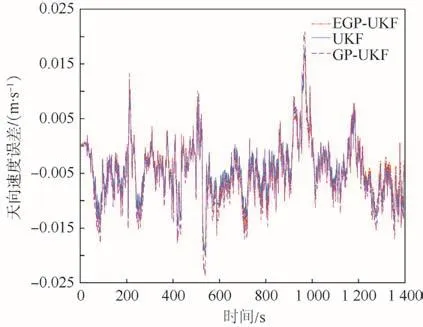
圖7 天向速度誤差對比Fig.7 Comparison of up velocity error

圖8～圖10表明，在航向角誤差、俯仰角誤差和橫滾角誤差方面，本文 EGP-UKF方法明顯優(yōu)于UKF和GP-UKF。可以看出，EGP-UKF的收斂速度比UKF和GP-UKF更快。此外，在航向角誤差方面 EGP-UKF與 UKF、GP-UKF幾乎是相同的。

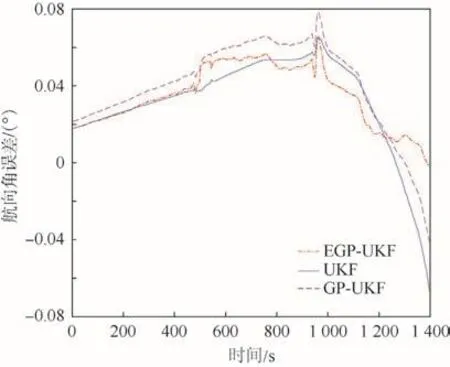
圖8 航向角誤差對比Fig.8 Comparison of heading angle error

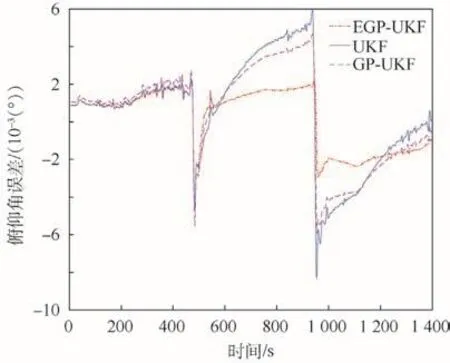
圖9 俯仰角誤差對比Fig.9 Comparison of pitch angle error

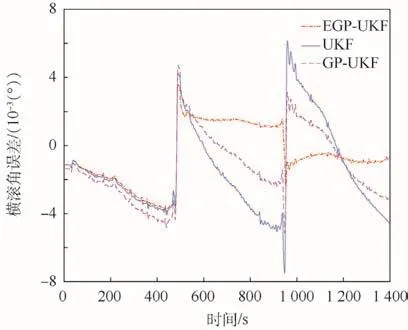
圖10 橫滾角誤差對比Fig.10 Comparison of roll angle error

本文定量分析了3種方法的性能。相比GPUKF和 UKF，本文 EGP-UKF在緯度誤差和經(jīng)度誤差分別降低了 18.5%、24.6%和 9.1%、10.6%。在高度誤差方面，這3種方法幾乎相同。東向速度誤差和北向速度誤差分別降低了42.5%、43.3%和22.6%、24.3%。因?yàn)樘煜蛩俣群透叨鹊南嚓P(guān)性，天向速度誤差幾乎是相同的。此外，航向角誤差、俯仰角誤差和橫滾角誤差分別降低了10.3%、30.1%、24.6%和3.4%、24.7%、28.2%。總之，EGP-UKF學(xué)習(xí)了UKF和其后處理平滑之間的殘差模型，通過該殘差模型提高了POS的測量精度。

在一般情況下，UKF的計(jì)算復(fù)雜度為狀態(tài)向量的維數(shù)的二次方。然而，GP在學(xué)習(xí)和預(yù)測過程中的計(jì)算復(fù)雜度分別是訓(xùn)練數(shù)據(jù)的三次方和二次方，故 GP-UKF比 UKF運(yùn)算速度慢，另外由于EGP-UKF融合了 GP和 UKF共同的優(yōu)點(diǎn)，所以EGP-UKF的運(yùn)算速度比GP-UKF慢。

5 結(jié) 論

1）針對傳統(tǒng)非線性濾波模型不確定性的問題，提出了增強(qiáng) GP的UKF方法。該方法既充分利用了GPR和UKF的優(yōu)點(diǎn)，又克服了它們自身的缺點(diǎn)。

2）該方法的核心是通過非參數(shù) GP學(xué)習(xí)UKF的狀態(tài)方程、量測方程和后處理平滑之間的殘差。

3）車載實(shí)驗(yàn)結(jié)果表明，與 UKF、GP-UKF相比，EGP-UKF具有更高的估計(jì)精度，因?yàn)?EGPUKF不僅具有更強(qiáng)的不確定度預(yù)測能力，而且具有更強(qiáng)的泛化能力。

4）如何提高EGP-UKF的實(shí)時(shí)性是未來的一個(gè)研究方向。