“建模—析模—用模”策略在生物學教學中的運用

蔣 進 李 椿

(江蘇省泰興中學 泰興 225400)

普通高中生物學課程標準(2017年版)將模型納入基礎知識范疇，并將模型方法規定為高中學生必須掌握的科學方法之一[1]。本節課“種群數量的變化”教學采用“建模—析模—用模”的教學策略，引導學生運用所學知識分析并解決實際問題。

1 教材分析

“種群數量的變化”一節是人教版高中生物學教材(必修3)第4章第2節的內容。本節內容安排在種群的特征之后，學生已有相關知識作鋪墊。在自然界中，某種生物種群數量的變化往往會直接或間接地影響群落乃至生物圈中其他生物種群數量的變化，與日常生產生活實際聯系緊密。因此，本節內容不僅在本章中承上啟下，對于本模塊也是舉足輕重。本部分內容共需要2課時，本節課為第1課時，確定教學內容為： 數學模型的建構、分析及應用。

2 模型建構

建構主義認為，學習者的知識不是通過教師傳授獲得的，而是學習者借助于他人(包括教師或同學)，利用相關學習資料(書本或其他媒介)，主動建構知識的過程。所謂建構，不只是輸入信息，而是加工、分析、選擇、重組甚至改造已有的知識經驗，最終形成自己的新觀點的過程。用于表達生命活動規律的計算公式、函數式，以及由實驗數據繪制成的曲線圖、柱形圖和餅狀圖等都稱為數學模型。數學模型建構的基礎是數學方法，有利于提升學生的思維技能，形成簡約而嚴密的邏輯思維品質[2]。

活動1 建構大腸桿菌種群數量增長數學模型。大腸桿菌常通過分裂來增殖，將大腸桿菌接種到液體培養基中，每隔一段時間統計數量，繪制曲線可顯示其數量隨時間增加的情況： ①如果營養和空間不受限制，每隔20 min大腸桿菌數目加倍。在假設條件下，請你算出1個大腸桿菌產生的后代在不同時間的數量，并填入表1；②請在坐標紙上作圖： 為每個坐標軸選擇合適的刻度，并在刻度上做記號在圖上標出；③請描述自己畫出的曲線形狀，并嘗試說出該種群數量的增長特點。

表1 大腸桿菌數量變化情況記錄表

設計意圖： 讓學生根據材料提供的實例，通過計算、填表和繪圖來建構種群數量增長的“J”型曲線(參看圖2中曲線A)。讓學生先通過自主建構，再小組合作探究，感悟數學模型。

活動2 建構果蠅種群數量增長的數學模型。果蠅繁殖速度快、易計數和保存，常作為生態學研究的材料。實驗時，每天將14只發育程度相同的果蠅成蟲(雌雄各半)準確地放入相應編號的培養瓶之中。塞住瓶口后，置于相同條件下(25℃恒溫培養箱)培養，每隔1 d記錄各個瓶中的果蠅成蟲數量： ①統計果蠅成蟲數量完成表2，并根據數據繪制果蠅種群數量(假設成蟲： 幼蟲≈2∶5)的增長曲線；②請描述自己畫出的曲線形狀，嘗試說出該種群數量的增長特點；③開放式討論： 環境中的哪些因素會影響果蠅種群的繁殖？

課前進行了充分的準備工作，包括： 果蠅培養基的配制、果蠅的接種與培養以及果蠅種群數量計數板的設計與制作等。課堂上學生借助于相關用具(毛筆、牙簽等)將培養瓶中的果蠅成蟲轉移到計數板進行數量統計(表2)和數據處理(圖1)。

表2 果蠅成蟲數量變化情況記錄表(11月)

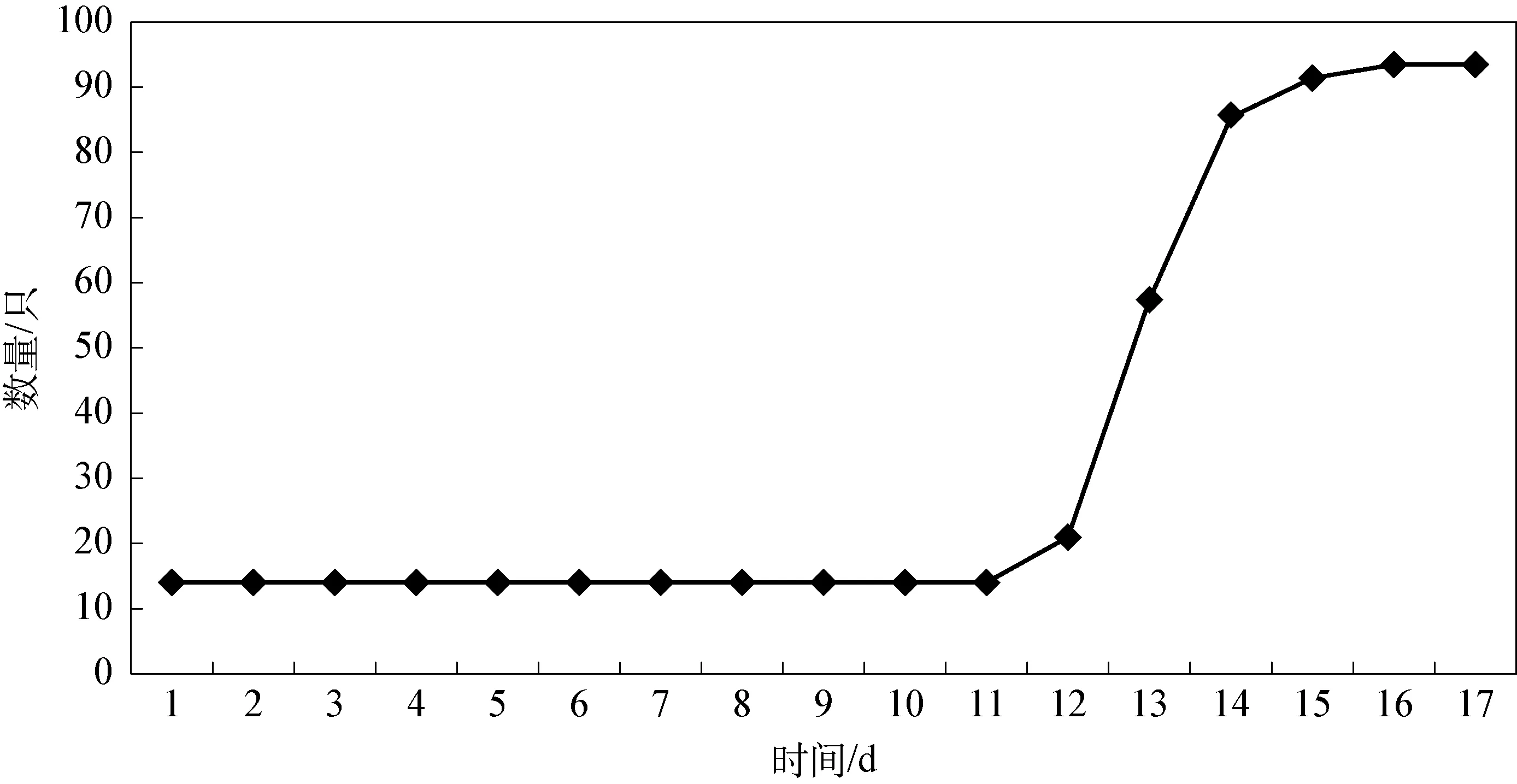
圖1 果蠅種群數量變化曲線圖注： 第1 d為培養瓶中的果蠅數量，第2 d為培養瓶中的果蠅數量，以此類推

設計意圖： 通過小組合作探究，學生自主地體驗果蠅培養的過程，參與果蠅成蟲數量的統計及種群“S”型增長模型的建構。學生明確并掌握種群“S”型增長的特點等相關基礎知識的同時，培養學生的科學思維和科學探究能力。

3 模型分析

模型分析即借助于模型，細致地尋找能夠解決實際問題的主線，并通過分析問題最終解決問題的一種科學思維活動。本節課由于時間和空間的限制，為了讓學生在課堂上能分析一個果蠅種群的數量隨時間變化的規律，教師讓學生統計不同時間接種，但在相同條件下培養的不同種群數量來模擬同一種群隨時間變化的情況。

活動3 對學生進行批判性思維的訓練。有興趣小組的學生連續20 d培養20個果蠅種群，數量統計如表3。通過小組合作討論并完成下列問題： ①結合構建的“J”型及“S”型增長模型(圖2)，嘗試分析種群數量變化的原因；②在種群數量減少時，怎樣做可能使種群開始增長？

表3 果蠅成蟲數量變化情況記錄表

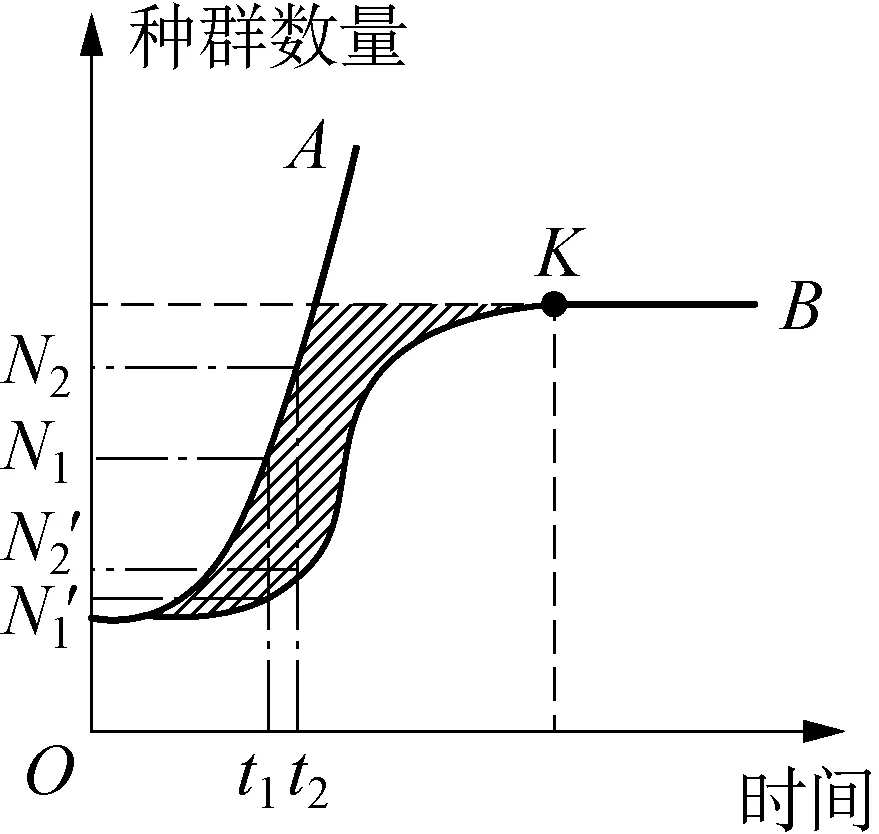
圖2 種群數量變化的兩種增長曲線

設計意圖： 引導學生分析進一步探究實驗條件下(連續培養果蠅20 d)曲線的變化趨勢。學生依據活動1和活動2的實例提供的兩種不同情境，結合構建的“J”型及“S”型增長數學模型分析得知： 培養早期由于食物和空間條件充裕，氣候適宜，種群數量急劇增長；培養的中后期由于受到資源和空間的限制，種內斗爭也在加劇，種群會停止增長并穩定在一定水平；隨著時間的推移，培養末期的不利生存條件最終會導致種群數量急劇下降甚至消亡。

活動4 比較“J”型及“S”型曲線的差異。假設圖2中A、 B是果蠅種群的兩種增長曲線，請討論并回答下列問題： ①曲線A、 B所示的增長方式分別在什么情況下發生？②請依據所學知識，嘗試說出圖中(N1-N1′)以及(N2-N2′)的含義。③嘗試說出陰影部分所表示的含義。

設計意圖： 在一系列問題的設置中，學生通過比較及歸納等分析方法，厘清了兩種增長曲線的適用范圍。同時，問題②為問題③作鋪墊，讓學生對“J”型及“S”型曲線的差異進行更透徹的分析，并得出結論： 陰影部分即表示現實條件中通過生存斗爭而被淘汰的個體。

4 模型應用

模型應用是指將所學知識運用于新的具體情境，包括原則、方法和規律的拓展。它代表較高水平的學習成果，需要建立在對知識點掌握的基礎之上。而引導學生應用數學模型方法解釋生命現象，揭示生命活動的規律是構建數學模型的著眼點。教師要引導學生在現實生活背景中學習生物學，并指導學生應用獲取的生物學知識指導生產實踐，解決實際問題。

活動5 ①資料1： 老鼠繁殖次數多、孕期短、產仔率高和性成熟快，數量能在短期內急劇增加。其適應性很強，常對農業生產釀成巨大災害。人們通常通過器械、藥物進行捕殺，但種群數量又很快恢復。因此，這種方法是治標但不治本。②資料2： 一位大熊貓研究專家發現： 由于棲息地減少和偷獵者的雙重打擊，白頭葉猴的數量比大熊貓還稀少。他建議要限制農民上山砍柴，并關閉采石場。最近報道，該地約20 km2的研究基地內，白頭葉猴已達800只左右。③資料3： 圖3所示的曲線可用于指導漁業捕撈，保證魚類資源的可持續發展。

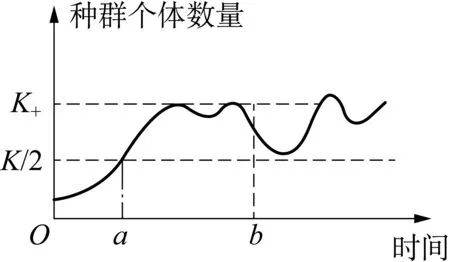
圖3 種群個體數量隨時間變化的曲線

根據資料進行分析討論。分析上述3則資料，指導學生進行開放式討論： ①為達到既治標又治本，試從環境容納量的角度思考可通過哪些措施控制鼠害？②結合資料2說說我國對大熊貓、白頭葉猴等珍稀動物的保護采取了哪些有效措施？其原理是什么？③漁業捕撈時，既要獲得魚類資源較大捕撈量，又要保證其高速增長。分析資料3，說說種群數量在何區間可以開捕？捕撈后剩余量宜為多少？

設計意圖： 在學生對J”型及“S”型增長數學模型有了感性和理性認識之后，結合相關資料，進一步運用嚴密的數學模型思維分析并解決具體問題。例如，通過改變環境容納量(K值)來有效地控制老鼠等有害動物的數量，來拯救大熊貓等瀕危的珍稀物種；在種群增長速度最快且種群數量恢復也較快的K/2值合理進行魚類資源的捕撈，以實現資源的可持續利用。這一系列實例都是種群數量“S”型增長數學模型在生產生活中的具體應用。

5 教學反思

本節課采用的“建模—析模—用模”教學策略，是數學模型在生物學研究中的一個典型例子，應該使學生舉一反三，不斷嘗試將數學方法滲透進生物學學科的學習中。數學模型的建構體現了跨學科的思想，用數學模型方法來反映生命活動的規律，更容易被學生接受，可起到事半功倍的效果。