基于改進PSO-BP神經網絡的冰蓄冷空調冷負荷動態預測模型
楊熊,于軍琪,郭晨露,華宇劍,趙安軍
(西安建筑科技大學 a.信息與控制工程學院;b.陜西省新型城鎮化與人居環境研究院,西安 710055)
隨著中國社會經濟的快速發展,能源短缺和環境惡化現象日益突出,沉重的能源負擔已成為阻礙經濟可持續發展的重要桎梏。其中,建筑能耗約占全社會總能耗的30%[1],在所有建筑中,大型公共建筑因其舒適度要求高、人流量大、空調系統運行時間長等原因,已成為建筑能耗中的“巨無霸”,其空調系統單位建筑面積能耗約為城鎮建筑的5倍[2]。作為緩解這種緊張局面的一種有效方式,冰蓄冷空調系統利用水/冰相變潛能儲存能量,使用夜間低價電制冰蓄冷,白天用電高峰融冰釋冷,以滿足建筑物的負荷需求,不僅對電網的電力負荷具有移峰填谷的作用,同時,也降低了用戶空調系統的運行費用。合理匹配谷段及峰段電價時間內制冷機組供冷和蓄冰裝置融冰供冷是冰蓄冷空調系統優化控制的核心問題,其中,準確的冷負荷動態預測數據更是冰蓄冷空調系統節能優化的首要因素。
當前,建筑冷負荷預測方法主要有回歸分析法、仿真模擬法和機器學習法。回歸分析法主要包括多元線性回歸模型(MLR)[3]、自回歸(AR)模型[4]。由于MLR模型在影響建筑冷負荷的多變量方面具有嚴重的非線性,因此,預測精度相對較低。AR模型輸入變量僅為建筑冷負荷的歷史數據,而沒有考慮其他因素,預測精度也很難滿足實際要求。常用的建筑冷負荷模擬軟件有TRNSYS[5-6]、ESP-r[7-8]和EnergyPlus[9-10]等,其在冷負荷預測過程中軟件程序效率較低,主要表現在:1)系統模型的建立需要花費較長的時間,并且模型也必須根據實際運行結果進行驗證和完善,才能產生高精度的輸出;2)由于模擬軟件通常用于空調系統的前期設計階段,因此,在系統運行階段難以提供準確、實時的指導控制;3)建模過程中參數設置對建模人員的專業化、工程經驗均要求高。綜上所述,傳統的仿真軟件程序不適合用于實際的系統管理。隨著人工智能AI(Artificial Intelligence)的快速發展,其中,BP(Back Propagation)神經網絡以其突出的非線性映射、自適應、容錯性強等特點,廣泛地應用于建筑冷負荷的動態預測[11-15]。然而,BP神經網絡具有局部最優、收斂速度慢、對訓練數據依賴性大的缺陷,往往又阻礙了其在實際工程中的應用。多數研究者采用粒子群優化算法PSO(Particle Swarm Optimization)的全局搜索能力優化BP神經網絡,極大地避免模型陷入局部最優的缺陷。然而,由于模型輸入變量與輸出變量相關性差、冗余度高導致的模型預測精度差的缺陷仍然沒有得到良好解決[16-17]。
筆者在傳統PSO-BP神經網絡全變量預測模型的基礎上,采用灰色關聯度分析法對模型輸入變量預處理,剔除相關性較低的因子,采用與輸出結果關聯度高的因子作為模型輸入變量預測大型公共建筑冰蓄冷空調系統動態冷負荷。研究表明,該改進模型相對于傳統PSO-BP神經網絡全輸入變量預測模型在預測精度、收斂速度方面均有較大的提高,滿足工程實際應用需求。
1 大型公共建筑冷負荷動態預測模型
1.1 灰色關聯度分析法
灰色關聯度分析法是一種多因素統計分析方法,以各因素的樣本數據為依據來描述輸入因素對輸出結果影響的強弱、大小和次序[18]。若輸入變量與輸出結果變化的趨勢、速度基本一致,則它們之間的關聯度較大;反之,關聯度較小。該方法避免了由于輸入變量不對稱帶來的損失,并且對數據要求較低,工作量較少,廣泛用于數據預處理。
1.2 PSO-BP神經網絡算法
PSO-BP神經網絡將粒子群優化算法引入BP神經網絡,利用PSO算法的全局搜索特性和BP算法快速局部搜索能力,達到良好的預測效果[19-21]。PSO-BP神經網絡模型,將網絡權值和閾值映射為種群粒子編碼,以樣本輸出值與期望值之差的絕對值之和為粒子適應度函數,通過反復迭代,最終獲得最優粒子,解碼后得到BP神經網絡全局最優權值和閾值。
2 基于改進PSO-BP神經網絡的大型公共建筑冷負荷動態模型
2.1 實驗數據來源與分析
實驗數據來源于西安賽格國際購物中心,該建筑物高40.6 m,總建筑面積25 萬m2,商業面積20 萬m2,分為地下兩層,地上八層,建筑空調面積18.76 萬m2,夏季空調采用部分蓄冷的冰蓄冷空調系統。
冰蓄冷空調冷負荷預測訓練樣本的輸入層節點通常為T時刻室外空氣溫度、濕度、太陽輻射強度、室外風速[22-25],考慮到太陽輻射、室外溫度會導致建筑空調冷負荷存在嚴重的滯后現象,因此,在預測模型中還加入了T-1 h時刻室外空氣溫度、太陽輻射強度[26]。考慮到空調冷負荷的時間序列性,相關研究還加入了T-1 h時刻空調冷負荷、T-2 h時刻空調冷負荷、T-3 h時刻空調冷負荷以及T-24 h時刻空調冷負荷作為模型輸入變量。輸出層節點為T時刻空調預測冷負荷。
實驗以6月、7月空調系統逐時冷負荷數據、室外干球溫度數據、室外空氣濕度以及太陽輻射強度等變量做為訓練數據,采用8月份數據對模型進行驗證分析,如圖1所示。3個月的室外氣象參數與空調冷負荷均具有強烈的關聯性,3個月某日中空調冷負荷隨著室外氣象參數的變化發生相應的變化:室外溫度、太陽輻射強度與空調冷負荷正相關,室外濕度與空調冷負荷負相關。
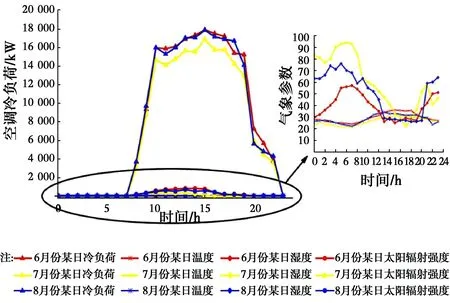
圖1 6月、7月、8月空調冷負荷與室外氣象參數曲線圖Fig.1 Air-conditioning cooling load and outdoor meteorological parameters in June, July and
2.2 輸入變量關聯性分析
采用灰色關聯度分析法,計算輸入變量與輸出結果間灰色關聯度,具體步驟如下。
step1:采用式(1),建立相關指標的原始數據矩陣xi;
xi=(xi(0),xi(1),xi(2)...,xi(23))
(1)
式中:xi(0),xi(1),xi(2)...,xi(23)分別表示第i個變量在0:00—23:00時刻的值。
step2:采用式(2),建立初始化變化矩陣
xi(2)/xi(0),...xi(23)/xi(0))=
(2)
step3:采用式(3),求差序列Δoi(k);
(Δoi(0),Δoi(1),...,Δoi(23))
(3)
Step4:采用式(4)、式(5),計算關聯系數ξoi(k)和灰色關聯度γoi;
(4)
(5)
空調冷負荷動態預測模型各輸入變量與T時刻空調冷負荷灰色關聯度如表1。
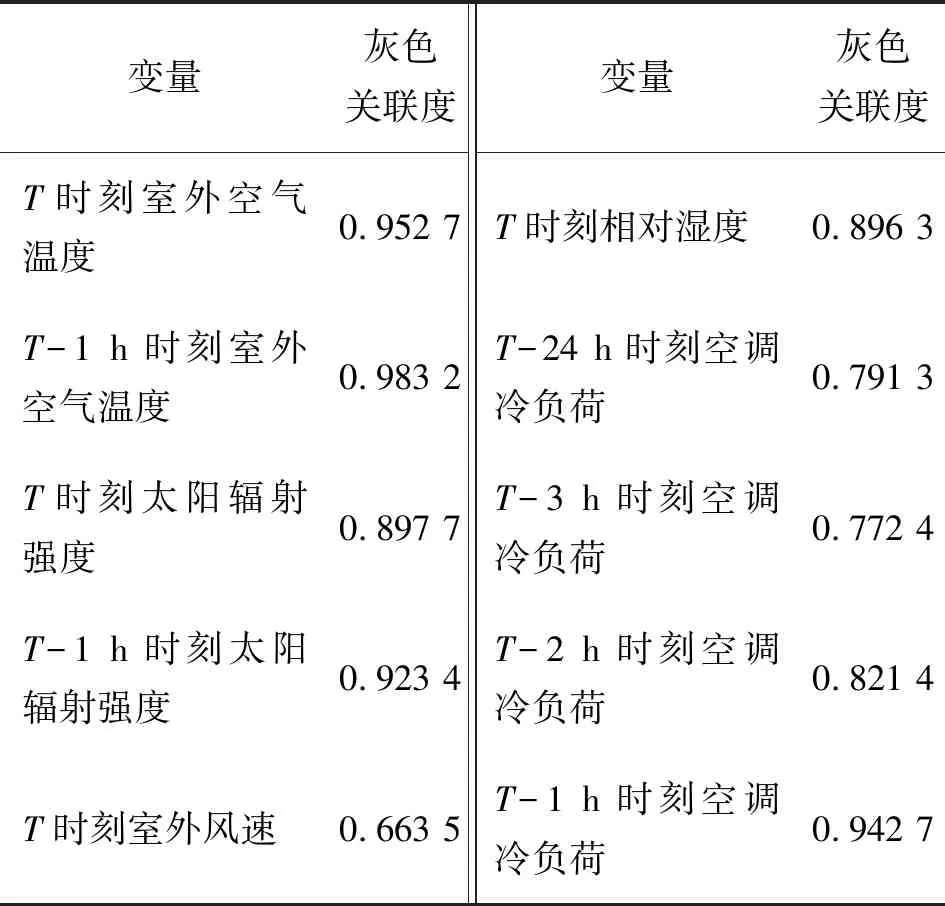
表1 各影響因子與T時刻空調冷負荷灰色關聯度Table 1 The impact of various factors andT timeair conditioning cooling load gray correlation
由上述分析可知,T時刻室外風速與T時刻空調冷負荷關聯度較小,關聯度系數僅為0.663 5,這是由于多數大型公共建筑采用封閉式的外圍護結構,沒有與外界形成自然通風,室內形成相對封閉的環境,因此,室外風速對空調系統冷負荷的影響較小;T-24 h時刻空調冷負荷與T時刻空調冷負荷關聯度為0.791 3,由于前一天與當天可能會存在較大的氣象參數差異,因此,相同時刻的空調冷負荷就會存在較大差異;T-3 h時刻空調冷負荷、T-2 h時刻空調冷負荷相對于T-1 h時刻空調冷負荷與T時刻空調冷負荷關聯度較低,為了降低僅由于歷史冷負荷對T時刻冷負荷的耦合作用,僅采用關聯度較高的T-1 h時刻空調冷負荷作為歷史冷負荷影響T時刻預測冷負荷的關鍵因素;T時刻室外空氣溫度、濕度、太陽輻射強度與T時刻空調冷負荷表現出較高的關聯性,這與多數大型公共建筑冷負荷影響因素研究的結論一致[4,7,11,15,27-28]。由于室外空氣溫度、太陽輻射強度對大型公共建筑空調冷負荷存在嚴重的滯后性,因此,T-1 h時刻室外空氣溫度、太陽輻射強度與T時刻空調冷負荷關聯度也較高。
綜上分析,確定T時刻室外空氣溫度、T-1 h時刻室外空氣溫度、T時刻室外空氣濕度、T時刻太陽輻射強度、T-1 h時刻太陽輻射強度、T-1 h時刻空調冷負荷為影響T時刻空調冷負荷的關鍵因素。
2.3 基于PSO-BP神經網絡模型進行大型公共建筑動態冷負荷預測
基于上述對預測模型輸入變量的分析,實驗采用3層BP神經網絡結構,輸入層神經元數為6,T時刻空調冷負荷數據為輸出層,故輸出層神經元數為1,隱含層因子數由經驗式(6)得出為13。隱含層節點采用tansig轉移函數,輸出層節點采用purelin轉移函數。
m=2n+1
(6)
式中:m為隱含層神經元個數;n為輸入層神經元個數。
1)由于神經網絡訓練函數的活性范圍為[0,1],采用式(7)離差標準化對輸入數據進行處理。
(7)
2)初始化粒子群的規模,包括種群粒子個數N、粒子個體長度D、粒子的初始速度、位置。
試驗中粒子數N取值為100,粒子個體長度D的計算式為
D=S1S2+S2S3+S2+S3
(8)
式中:S1、S2、S3分別為BP神經網絡輸入層因子數、隱含層因子數、輸出層因子數。計算得D=105。
3)粒子適應度計算。以預測值和觀測值的誤差絕對值之和作為粒子適應度值F,計算公式為
(9)
式中:n為樣本數;yi為樣本i的觀測值;Oi為樣本i的預測值。
4)粒子適應度比較。比較規則為:
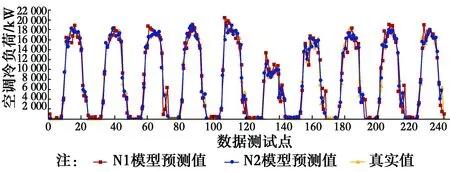
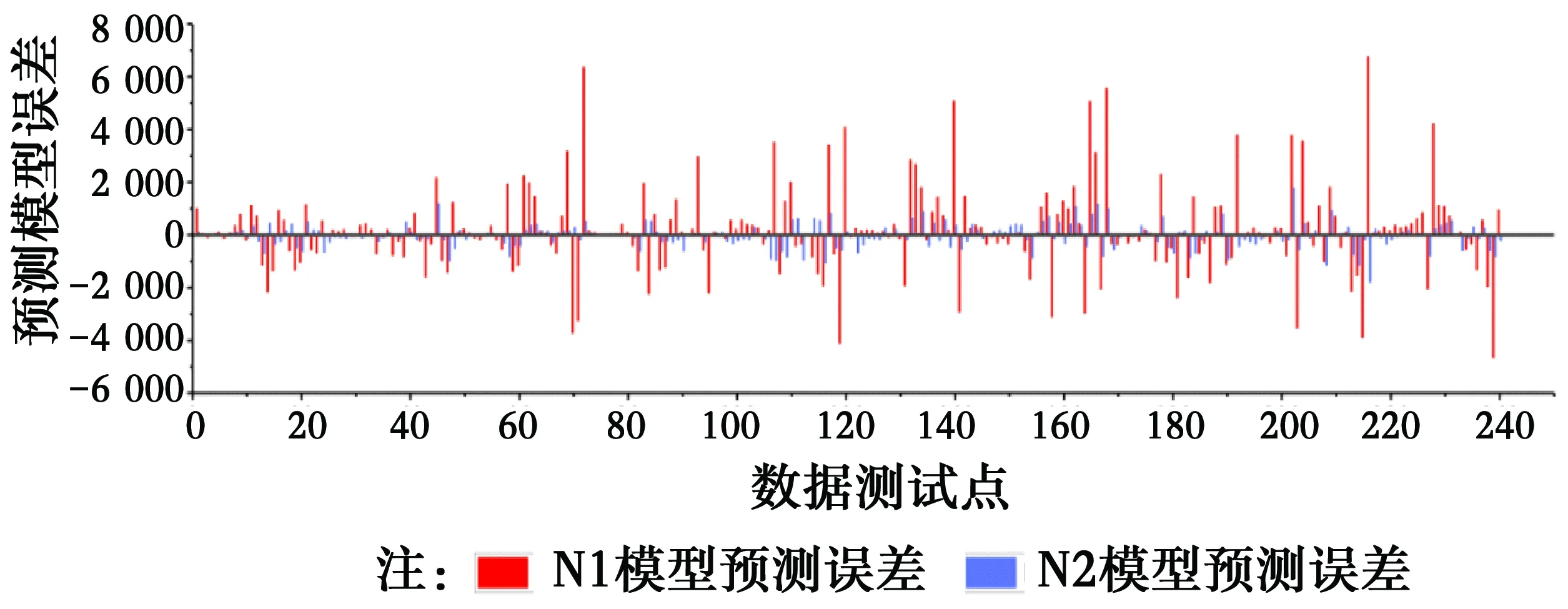
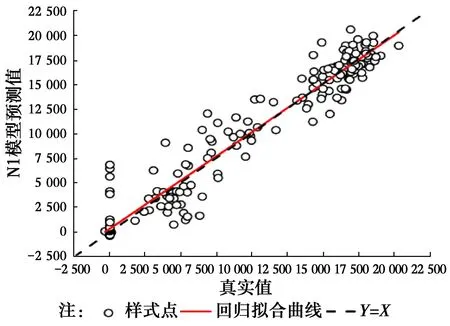
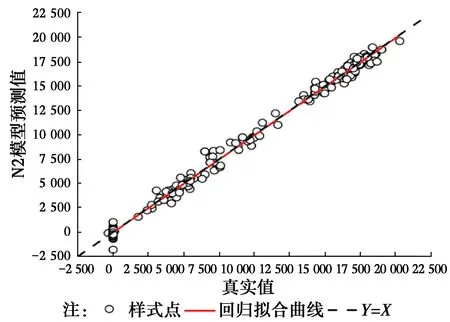
如果sse 如果sse 其中:sse是粒子的當前適應值;pbestfitness是粒子的個體最優適應值;gbestfitness是種群全局最優適應值;pbest是粒子個體最優值;gbest是種群全局最優值;xi為當前計算粒子。 5)粒子位置及速度的更新。采用式(10)、式(11)進行粒子速度及位置的更新。 (10) (11) 6)當前迭代次數Epoch與最大迭代次數tmax比較,若Epoch>tmax,則終止算法,當前的gbest為BP神經網絡優化的權值和閾值,否則跳至步驟2),繼續下一次迭代。 兩種模型的預測結果如圖2所示,其中,N2預測模型為采用本文提出的改進算法建立的模型,N1預測模型為采用傳統PSO-BP神經網絡的全輸入變量算法建立的模型。由圖2可知,采用N2預測模型的預測精度高于N1預測模型。為進一步得出兩種預測模型誤差對比,圖3給出了兩種模型的絕對誤差,由圖3可見,N2預測模型的絕對誤差遠小于N1預測模型。 圖2 兩種模型預測值與空調冷負荷真實值曲線圖Fig.2 Two model predicted values and air conditioning cooling load actual value 圖3 兩種模型預測值與空調冷負荷真實值絕對誤差柱狀圖Fig.3 The absolute errors between the real values of the air conditioning cooling load and the two 以RMSPE(Root mean square percentage error)(式(12))均方根相對誤差作為兩種預測模型誤差評價指標, (12) 圖4 N1模型預測值與真實值回歸擬合曲線Fig.4 The regression fitting curve between the predicted value of N1 model and the real 圖5 N2模型預測值與真實值回歸擬合曲線Fig.5 The regression fitting curve between the predictedvalue of N2 model and the real 提出一種基于改進PSO-BP神經網絡算法,實現對冰蓄冷空調動態冷荷的準確預測,結論為:基于灰色關聯性分析法,確定影響冰蓄冷空調系統冷負荷的關鍵因素,并以此作為PSO-BP神經網絡預測模型的輸入變量,相對于傳統PSO-BP神經網絡全輸入變量預測模型,改進模型在預測精度、收斂速度方面均有較大提高,滿足工程實際需求,對大型公共建筑冰蓄冷空調系統的優化運行管理有重要的應用價值。
3 預測結果分析
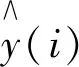
4 結論

