淺談直觀在數學教學中的作用
張明東

學生們的數學學習是需要由感性認識上升到理性認識,這樣才能夠深化對于知識的理解,更好地掌握知識。因此在數學教學中特別強調直觀教學的作用,因為它能夠直接、真實的給學生呈現知識,很好的彌補學生抽象思維能力的不足,同時直觀呈現知識也能夠使學生們對于知識更親切,降低學生們學習中畏難的心理障礙。在數學直觀教學中,我們可以借助教具實現直觀呈現,當然更多的是通過現代化的多媒體信息技術來給學生直觀呈現,通過圖形的變化、色彩的對比或者動畫的移動來更具體呈現。同時,隨著新課程的推進,數學核心素養目標的提出,對于數學直觀教學的重要性更加凸顯,就這一問題筆者談一談自己的認識。
一、利用多媒體實現直觀教學
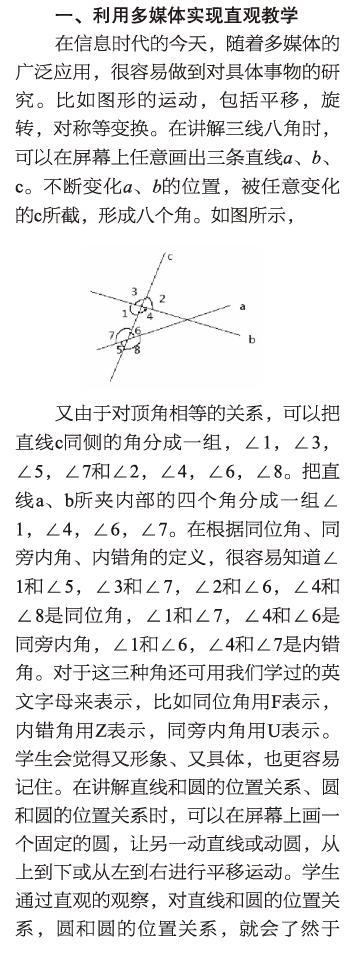
在信息時代的今天,隨著多媒體的廣泛應用,很容易做到對具體事物的研究。比如圖形的運動,包括平移,旋轉,對稱等變換。在講解三線八角時,可以在屏幕上任意畫出三條直線a、b、c。不斷變化a、b的位置,被任意變化的c所截,形成八個角。如圖所示,
又由于對頂角相等的關系,可以把直線c同側的角分成一組,∠1,∠3,∠5,∠7和∠2,∠4,∠6,∠8。把直線a、b所夾內部的四個角分成一組∠1,∠4,∠6,∠7。在根據同位角、同旁內角、內錯角的定義,很容易知道∠1和∠5,∠3和∠7,∠2和∠6,∠4和∠8是同位角,∠1和∠7,∠4和∠6是同旁內角,∠1和∠6,∠4和∠7是內錯角。對于這三種角還可用我們學過的英文字母來表示,比如同位角用F表示,內錯角用Z表示,同旁內角用U表示。學生會覺得又形象、又具體,也更容易記住。在講解直線和圓的位置關系、圓和圓的位置關系時,可以在屏幕上畫一個固定的圓,讓另一動直線或動圓,從上到下或從左到右進行平移運動。學生通過直觀的觀察,對直線和圓的位置關系,圓和圓的位置關系,就會了然于心,記憶深刻。
二、數形結合實現直觀教學
華羅庚先生說:“數無形,少直觀,形無數,難入微。”像數軸的運用,坐標系的運用,函數圖像的運用等等。比如二次函數的教學,在求解函數的有關問題時,若能恰當、巧妙地將數與形有機的結合并相互轉化,則可使求解的問題獲得直觀而簡捷、迅速而準確地解答。
例如:二次函數y=ax2+bx+c的圖像如上面右圖所示,則反比例函數y=ab/x 的圖像的兩個分支分別在第_____象限。
分析:本題關鍵確定ab的符號,注意觀察圖像的特點,從拋物線的開口方向和對稱軸x=-b/2a的位置易知a>0,-b/2a>0,即a>0,b<0,所以ab<0。故反比例函數y=ab/x的圖像的兩個分支分別在二、四象限。
說明:運用數形結合的思想將函數圖像與數量關系有機結合并相互轉化,這在解決有關函數問題時起著重要作用。
三、重視畫圖實現直觀教學
在數學教學中,對于圖形的分析是學生們數學學習的重要內容,而僅僅是腦子里想是無法實現具體、細致的分析的,需要結合具體的圖進行針對性的解析,所以要重視學生畫圖能力的培養,要培養學生的畫圖意識,同時逐漸掌握正確的畫圖習慣。具體來說,在教學中能通過畫圖更好解決問題的知識一定要要求學生去畫,其實質就是具體化、直觀化的呈現知識,有利于學生通過直觀的思維來實現感性認識到理性認識的飛躍。
其中,為了更好的進行直觀教學,對于學生動手操作能力培養非常重要。特別是一些幾何問題和函數問題。它是由學生實際執行的操作,具有不可替代的直觀性,為以后畫圖的精確性提供保障,更有利于問題的解決。現在我們強調讓學生自己動手,用折紙,度量,拼湊的方法進行幾何操作,尺規作圖正是這樣的活動。實際教學中,尺規作圖以嚴密的邏輯推理,成為數學教學中獨具一格的教學內容,由于其獨特的知識結構,多年來在初中教學中未有深入的涉及和研究,對學生的教學要求,只局限于五種基本尺規作圖法的理解和操作,隨著新課程對學生能力培養的要求,對尺規作圖的要求也提出了更高的要求:除了要熟練操作五種基本圖形作法外,還要結合幾何推理,對目標圖形進行作圖原理推究、作圖方法探索。這在一定程度上,對尺規作圖的課堂教學帶來了一定的挑戰。
總之,教師直觀在數學教學中的作用,以激發學生的學習興趣,增強他們的探索欲望,提高學生的幾何思維能力和實踐操作能力。
(作者單位:山東省淄博市淄川區淄河中學)

