空間曲線平移并聯機構構型綜合與分類

葉梅燕 石志新 羅玉峰,3

(1.南昌大學機電工程學院， 南昌 330031； 2.南昌大學理學院， 南昌 330031；3.華東交通大學機電與車輛工程學院， 南昌 330013)

0 引言

在管道焊接、曲面加工、軌跡追蹤等工程應用中，人們通常期望設計出執行構件能夠沿空間曲線運動的機械裝備。目前人們的設計思路大多基于外在幾何觀點(將空間曲線嵌入外圍3維歐氏空間)，即設計一個三平移機構，通過算法協調控制3個方向的移動輸出，實現執行構件沿指定空間曲線作平移運動。然而根據高斯非歐幾何的內蘊思想(將曲線和曲面本身視為獨立空間)，空間曲線屬于1維幾何形體，若采用1自由度的曲線平移機構替代上述三平移機構，則可實現減少自由度、降低控制難度、節約成本的目的。因此，研究簡單、實用的各類曲線平移機構十分必要。

目前機器人機構構型綜合的方法主要有：基于螺旋理論的方法[1-6]、基于位移子群/流形的運動綜合方法[7-11]、基于線性變換與進化形態學的方法[12-13]、基于方位特征集的方法[14-20]以及基于GF集的綜合方法[21-24]。然而，這些理論方法均難以直接應用于具有彎曲平移(沿曲線或曲面平移)運動特征的機構，原因為：①缺少可描述彎曲平移運動特征的表達模型。②過于強調局部運動特征，缺少平移空間整體形態特征。③缺少彎曲平移運動特征的運算規則。對于彎曲平移機構而言，由于移動方向時刻變化，因此局部運動特征不能反映整體形態特征，而且基于線性空間的運動特征求交和求并運算規則不再適用。

本文根據內蘊幾何思想，建立可描述彎曲平移運動特征的表達模型，研究機器人機構末端構件彎曲平移運動的形成機理及其基本類型，制定彎曲平移運動特征的運算規則，并結合實例提出空間曲線平移并聯機構的構型綜合方法。

1 可描述彎曲平移運動特征的表達模型

剛體運動包括平移和轉動2種基本運動類型，因此機器人末端構件的運動特征應由平移特征和轉動特征共同組成。

(1)旋轉特征。轉動特征可由旋轉軸數量和方向來表征。

(2)平移特征。平移運動包括平直移動(沿直線或平面平移)和彎曲平移(沿曲線或曲面平移)2種情況。如平行四邊形機構的連桿作圓周曲線平移運動，3-UU機構[21]的動平臺沿球面作平移運動等。由于彎曲平移的移動方向時刻變化，因此其運動特征需要由平移空間的維數、整體形態以及生成方式三者共同表達。

綜合考慮旋轉特征和平移特征，本文采用的末端構件運動特征描述模型為

(1)

式中M——末端構件的運動特征集

t——平移

p——平移空間的維數(獨立平移數目)

w——平移空間的整體形態

N——平移空間的生成方式

r——轉動

q——獨立旋轉方向矢量的數目

S——旋轉軸方向單位矢量組成的集合

基于內蘊幾何學的基本思想，直線和曲線可被視為1維獨立平移空間，平面和曲面則被視為2維獨立平移空間。0維和3維平移空間無需記錄整體形態和生成方式，故其移動特征可分別表示為t0和t3。0維和3維轉動空間無需記錄旋轉軸方向，其轉動特征分別表示為r0和r3。1維和2維轉動空間的轉動特征分別表示為r1(l)和r2(l1,l2)，其中l、l1和l2均為旋轉軸方向的單位矢量。

2 支鏈末端構件彎曲平移運動的形成

由于支鏈(串聯機構)是由若干個運動副依次串聯而成，因此其末端構件的運動特征集是各運動副運動輸出特征的并集，可表示為

(2)

式中ML——支鏈末端構件的運動特征集

2.1 單自由度運動副的運動輸出特征

機器人機構的運動副類型較多，常見運動副包括：轉動副(R副)、移動副(P副)、球副(S副)、胡克鉸(U副)、圓柱副(C副)等。為了分析方便，可采用運動副等效替換的方法將它們簡化為只含轉動副和移動副。如球副等效為3個軸線匯交于1點的轉動副，胡克鉸等效為2個軸線垂直正交的轉動副，圓柱副等效為共軸的轉動副和移動副。

(1)P副的運動輸出特征。由于P副僅產生直線平移運動，其移動空間整體形態為直線，并且該移動空間由P副生成，由式(1)可知，移動副的運動輸出特征可表示為t1(直線,P)，其中P為P副方向的單位矢量。

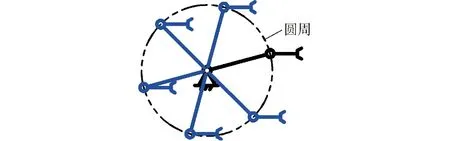
圖1 R‖R機構及其末端構件的平移空間Fig.1 R‖R mechanism and translation space of its end-effector

(2)R副的運動輸出特征。轉動副不僅能產生繞其軸線的運動，而且可衍生出垂直于軸線方向的圓周曲線平移運動，即其運動特征具有二重性，可按如下規則選取：①優先取旋轉運動作為運動輸出特征，記為r1(R)，其中R為R副軸線方向的單位矢量。②若已有運動副產生了與該轉動副旋轉方向相同的旋轉運動，則該轉動副將會衍生圓周曲線平移(圖1)，此時應取衍生圓周曲線平移作為其運動輸出特征，記為t1(圓,R┴)，其中R┴表示由R副衍生且與R垂直的圓周平移運動。

2.2 2維曲面平移運動的形成及其類型

2維曲面平移空間是由2個1維平移空間合并而成，而且二者不能均為直線，即其中至少1個1維平移空間應為圓周。

2.2.1t1(直線)與t1(圓)的求并運算規則

由2.1節可知，1維圓周平移空間存在2種生成方式：一種由Pa副產生，另一種為兩平行R副衍生而成。

高校的課程設置不僅決定一個專業的定位，決定專業的寬度和廣度，更決定未來所培養學生的視野、知識儲備、專業傾向等綜合素質，是高校辦學中非常重要的環節。地方本科高校無論歷史沉淀、師資力量、學生素質還是整體綜合實力，與綜合性大學相比，差距都是非常大的。在這種情況下，扎根當地，發掘能夠體現地方價值與特色的課程就顯得尤為重要。

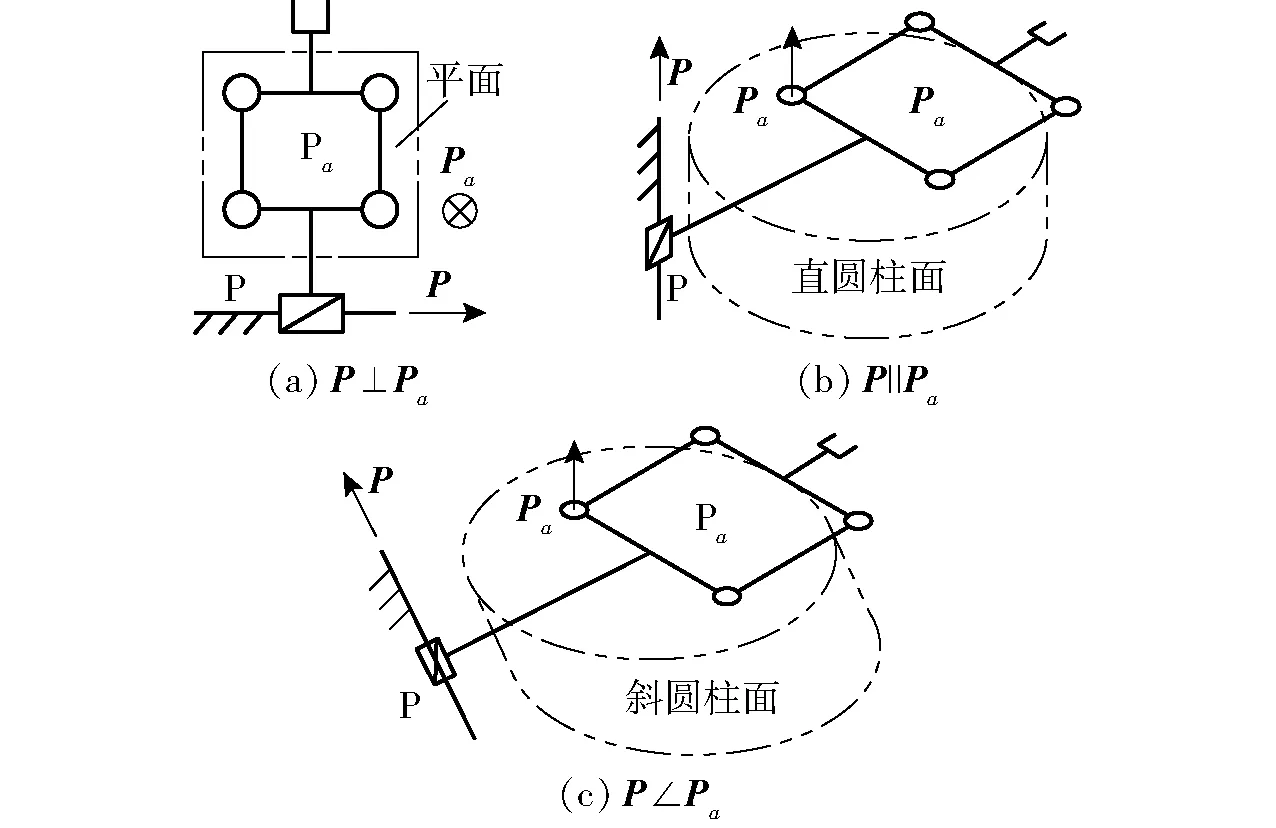
圖2 P-Pa機構及其末端構件的平移空間Fig.2 P-Pa mechanisms and translation spaces of theirs end-effector

(2)當1維圓周平移空間由兩平行R副衍生而成時，P副與它們在各種裝配關系下的合成2維平移空間如圖3所示，因此t1(直線,P)與t1(圓,R┴)的求并結果如下：

當P⊥R時，二者合成的平移空間為平面(圖3a)，故此時t1(直線,P)與t1(圓,R┴)的求并結果記為t2(平面,R)。

當P‖R時，二者合成的平移空間為直圓柱面(圖3b)，故此時t1(直線,P)與t1(圓,R┴)的求并結果為t2(直圓柱面,P⊕R┴)。

當P∠R且P副位于兩平行R副兩邊時，二者合成的平移空間為斜圓柱面(圖3c)，故此時t1(直線,P)∪t1(圓,R┴)=t2(斜圓柱面,P⊕R┴)。

當P∠R且P副位于兩平行R副中間時，二者合成的平移空間為圓錐面(圖3d)，故此時t1(直線,P)∪t1(圓,R┴)=t2(圓錐面,P⊕R┴)。

RPR機構(圖3)的末端構件除了具有2維平移特征外還具有繞R旋轉的1維轉動特征。

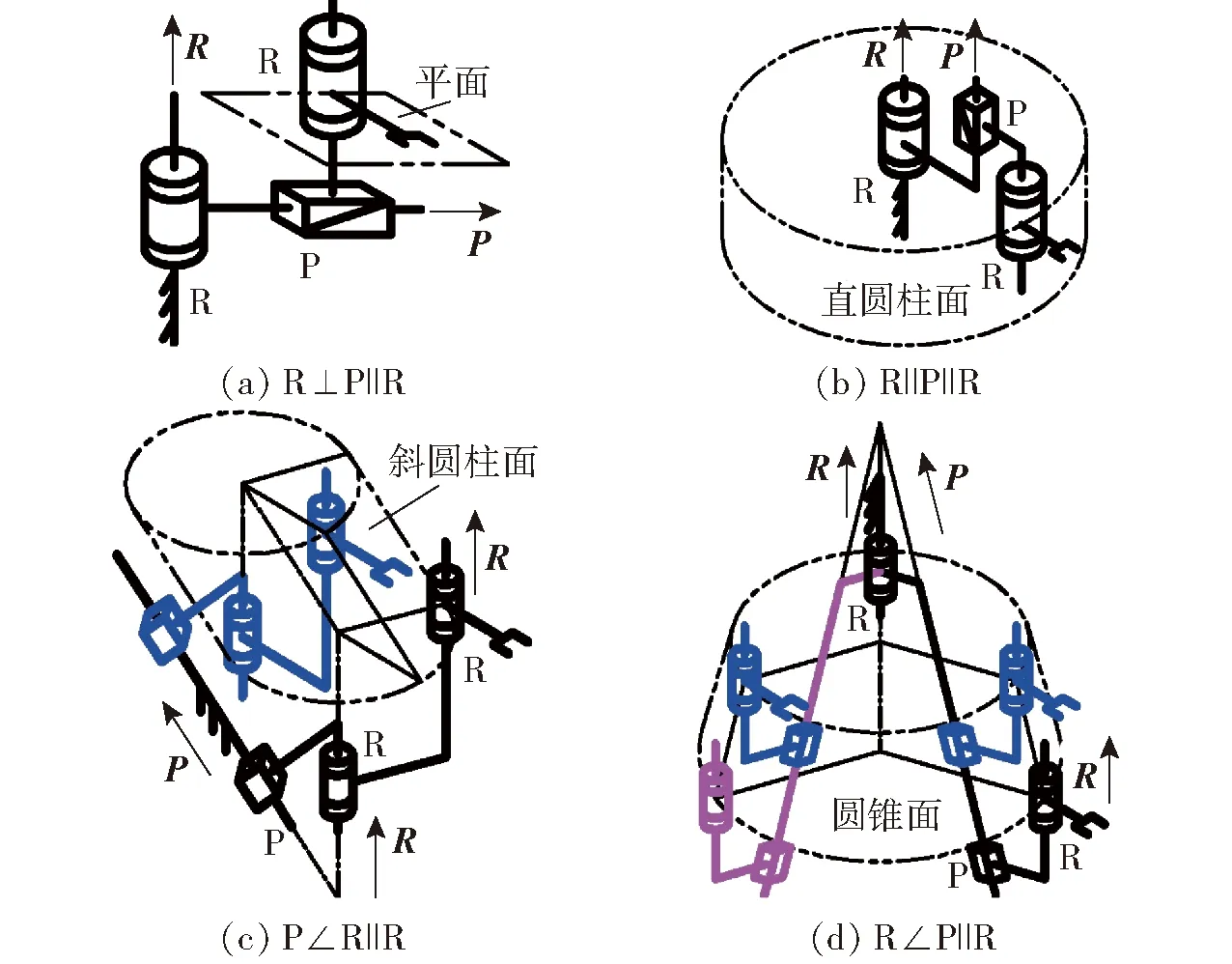
圖3 RPR機構及其末端構件的平移空間Fig.3 RPR mechanisms and translation spaces of theirs end-effector

2.2.2t1(圓)與t1(圓)的求并運算規則

兩圓周平移存在3種生成方式：兩圓周平移均由Pa副產生、兩圓周平移均由R副產生、兩圓周平移分別由Pa副和R副產生。由于上述3種生成方式下的合成平移空間類型均相同，因此無需分別討論。

兩圓所在的平面存在平行、相交(包括垂直和斜交)2種位置關系，且兩圓心的位置存在重合與不重合2種情況。上述各種方位關系對應的機構示例如圖4所示。

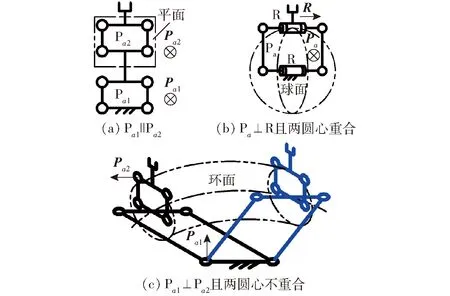
圖4 兩圓周平移合成各類2維空間的實例Fig.4 Examples of 2-dimension space generated by two circular-translation motion

綜合上述分析結果可以得出，支鏈末端構件的2維曲面平移空間存在圓柱面(包括直圓柱面和斜圓柱面)、圓錐面、球面、環面這4種基本類型。

3 空間曲線平移并聯機構的構型綜合

3.1 空間曲線平移并聯機構的基本類型

并聯機構由靜平臺(機架)、動平臺以及若干條支鏈組成。由于動平臺是在各支鏈共同作用下進行運動，因此其運動特征是各支鏈末端構件運動特征的交集。又考慮到空間曲線可看作空間兩曲面的交線，因此空間曲線平移并聯機構可由2條具有2維彎曲平移運動特征的支鏈構成。

根據第2節分析結果可知，支鏈末端構件的2維曲面平移空間存在4種形態(圓柱面、圓錐面、球面、環面)。考慮到這些曲面兩兩的交集一般為1條空間曲線(稱為相貫線)，因此空間曲線平移并聯機構可按曲線形態劃分為9種基本類型：柱柱相貫線平移機構、柱錐相貫線平移機構、柱球相貫線平移機構、柱環相貫線平移機構、錐錐相貫線平移機構、錐球相貫線平移機構、錐環相貫線平移機構、球環相貫線平移機構和環環相貫線平移機構。兩球面的交線為圓(屬于平面曲線)，它不屬于空間曲線。

本文僅對上述9種基本類型中的前2類并聯機構進行構型綜合，其余7類機構可以采用類似方法綜合得到。

3.2 柱柱相貫線平移機構構型綜合

3.2.1具有2維圓柱面平移特征的支鏈

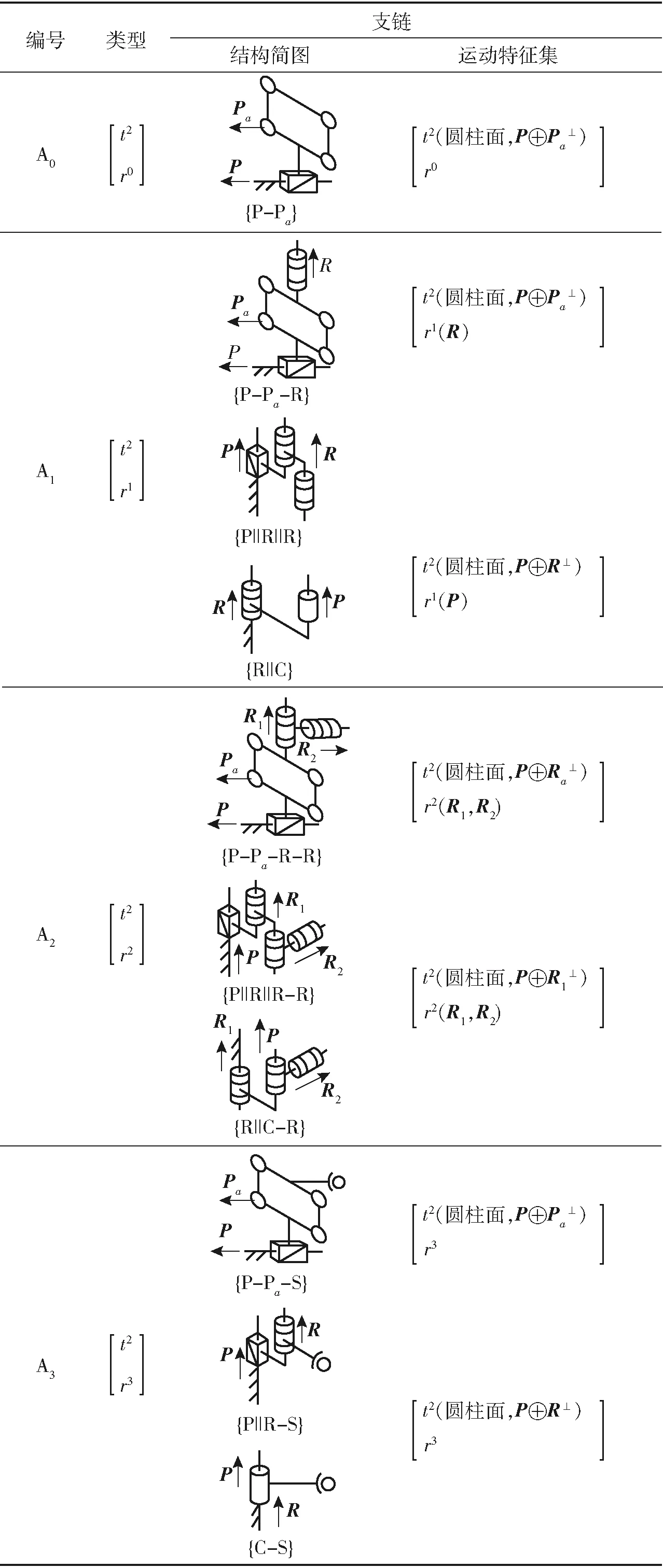
根據2.2.1節分析結果可知，2維圓柱面平移空間由直線平移和圓周平移合成產生，并且直線和圓所在的平面不能平行。具有2維圓柱面平移特征的支鏈結構類型如表1所示。

表1 具有2維圓柱面平移特征的支鏈
Tab.1 Branches with 2-dimension cylindertranslation characteristic

3.2.2支鏈組合方案

根據3.1節分析結果可知，柱柱相貫線平移機構可由表1中某2條支鏈(記為支鏈1和支鏈2)構成。為保證動平臺沿柱柱相貫線作純平移運動(不含轉動)，支鏈1、2的組合方案如表2所示。

表2 柱柱相貫線平移機構支鏈組合方案Tab.2 Branch assembling schemes of cylinder-cylinder intersection line translation mechanisms

3.2.3支鏈裝配幾何條件

(1)t2(圓柱面)與t2(圓柱面)的求交運算規則

當兩圓柱面的軸線平行時，二者的交線為平行于軸線的直線；否則，二者的交線為空間曲線(柱柱相貫線)。因此，2維彎曲平移特征t2(圓柱面)與t2(圓柱面)的求交運算規則為

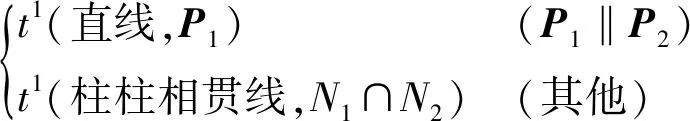
(3)

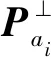
(2)兩支鏈裝配幾何條件分析

根據預期設計目標，支鏈1和支鏈2的運動特征集應滿足

(4)

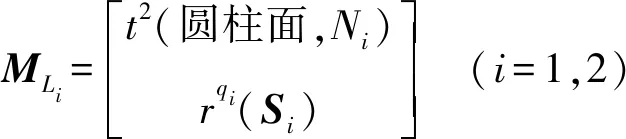
式中qi——支鏈i末端構件旋轉方向矢量的數目

Si——支鏈i末端構件旋轉方向單位矢量組成的集合

結合式(3)，可知式(4)成立的條件為P1與P2不平行且S1∩S2=?(空集)。因此表2中各組合方案對應裝配條件如下：

(1)組合方案1～4。支鏈1、2分別為表1中支鏈結構類型庫A0和Ai(i=0,1,2,3)。由于支鏈1的轉動特征為r0(表1)，故此時S1∩S2=?恒成立，因此支鏈1、2的裝配條件為P1與P2不平行。

(2)組合方案5。支鏈1、2均為表1中支鏈結構類型庫A1，二者的轉動特征可分別記為r1(R1)和r1(R2)。此時S1∩S2=?成立的充要條件為R1與R2不平行，因此支鏈1、2的裝配條件為P1與P2不平行且R1與R2不平行。

(3)組合方案6。支鏈1、2分別為支鏈結構類型庫A1和A2，二者轉動特征分別為r1(R)和r1(R1,R2)(表1)。此時S1∩S2=?成立的條件為R與R1、R2均不平行，故支鏈1、2的裝配條件為P1與P2不平行且R與R1、R2均不平行。

3.2.4柱柱相貫線平移機構

根據上述支鏈組合方案和裝配幾何條件，可綜合得到25種柱柱相貫線平移機構。表2中組合方案1～6生成的代表性機構如圖5所示。

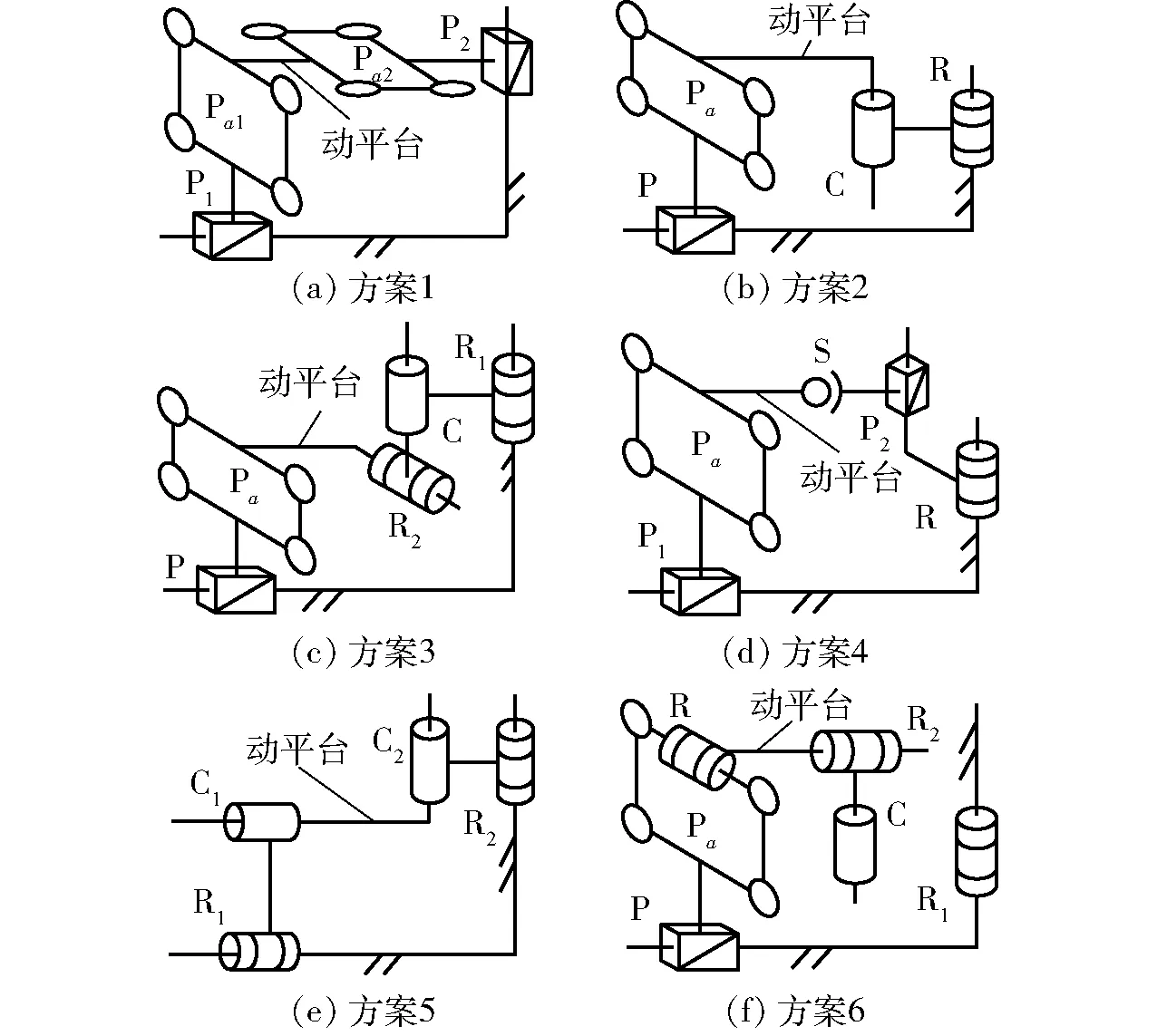
圖5 表2各組合方案生成的代表性并聯機構Fig.5 Representative mechanisms generated by assembling schemes in Tab.2

3.2.5分析驗證

以圖5e所示機構為例，分析該機構動平臺的運動特征。

已知兩支鏈末端構件運動特征集為

其中Pi為圓柱副Ci軸線方向單位矢量。故二者的并集為

(5)

根據自由度計算公式[14]可知，該機構自由度為

式中fi——第i個運動副的自由度

dim——維數函數

由于R1與R2不平行，r1(R1)∩r1(R2)=r0，故該機構的動平臺不含轉動輸出，又由于自由度F等于1，因此該機構的動平臺僅沿兩圓柱相貫線作彎曲平移運動(圖6)。

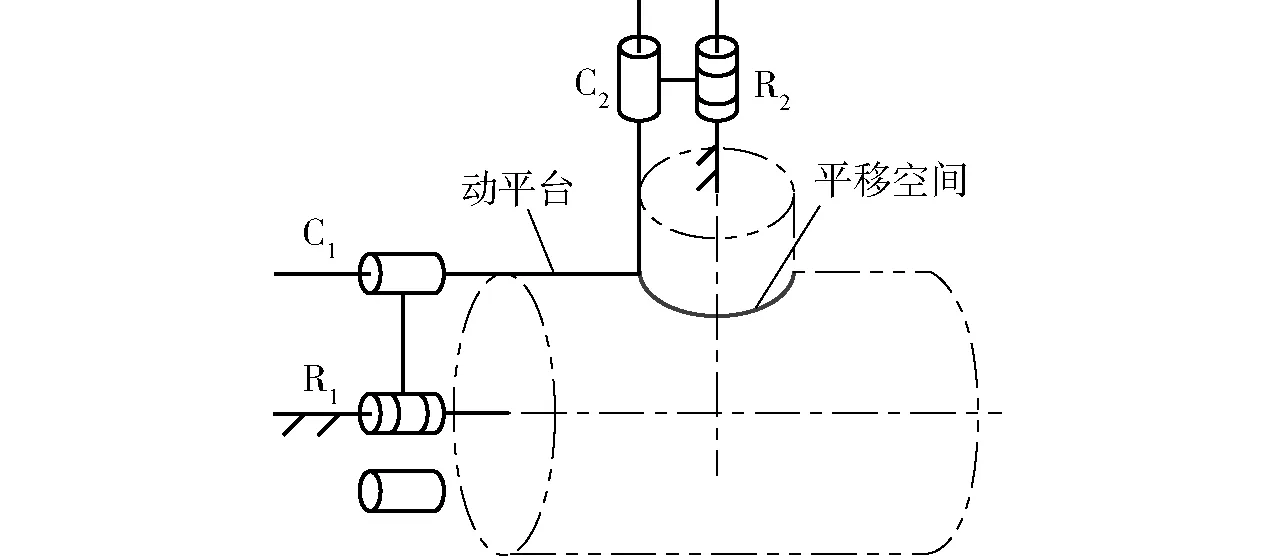
圖6 R‖C-C‖R機構及其動平臺的平移空間Fig.6 R‖C-C‖R mechanism and translation space of its end-effector

3.3 柱錐相貫線平移機構構型綜合

3.3.1具有2維圓錐面平移特征的支鏈

根據2.2.1節分析結果可知，2維圓錐面平移空間產生的條件為P副位于兩平行R副中間且P∠R。因此，具有2維圓錐面平移特征的支鏈結構類型如表3所示。

3.3.2支鏈組合方案

根據3.1節分析結果可知，可從表1、3中分別挑選1條支鏈(記為支鏈1和支鏈2)，二者共同構成柱錐相貫線平移機構。為保證動平臺僅沿柱錐相貫線作純平移運動(不含轉動)，支鏈1、2的組合方案如表4所示。

3.3.3支鏈裝配幾何條件

為保證動平臺無轉動輸出，兩支鏈末端構件轉動特征集的交集應為空集(即S1∩S2=?)，因此表4中各組合方案對應裝配條件如下：

(1)組合方案1～3。支鏈1均取自表1中支鏈結構類型庫A0。由于支鏈1的轉動特征為r0，故此時S1∩S2=?恒成立，因此支鏈1、2可任意裝配。

表3 具有2維圓錐面平移特征的支鏈
Tab.3 Branches with 2-dimension conetranslation characteristic

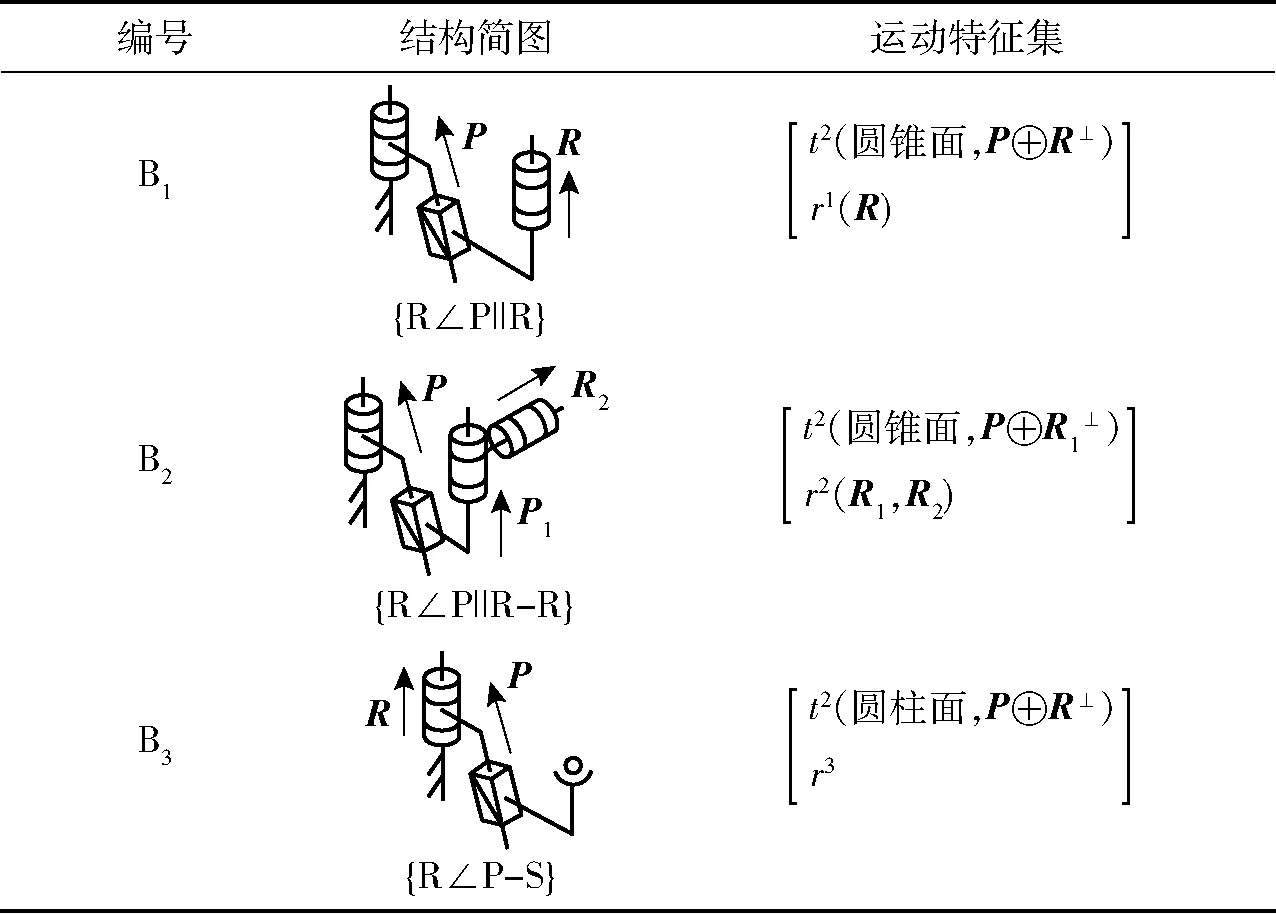
表4 柱錐相貫線平移機構支鏈組合方案Tab.4 Branch assembling schemes of cylinder-cone intersection line translation mechanisms

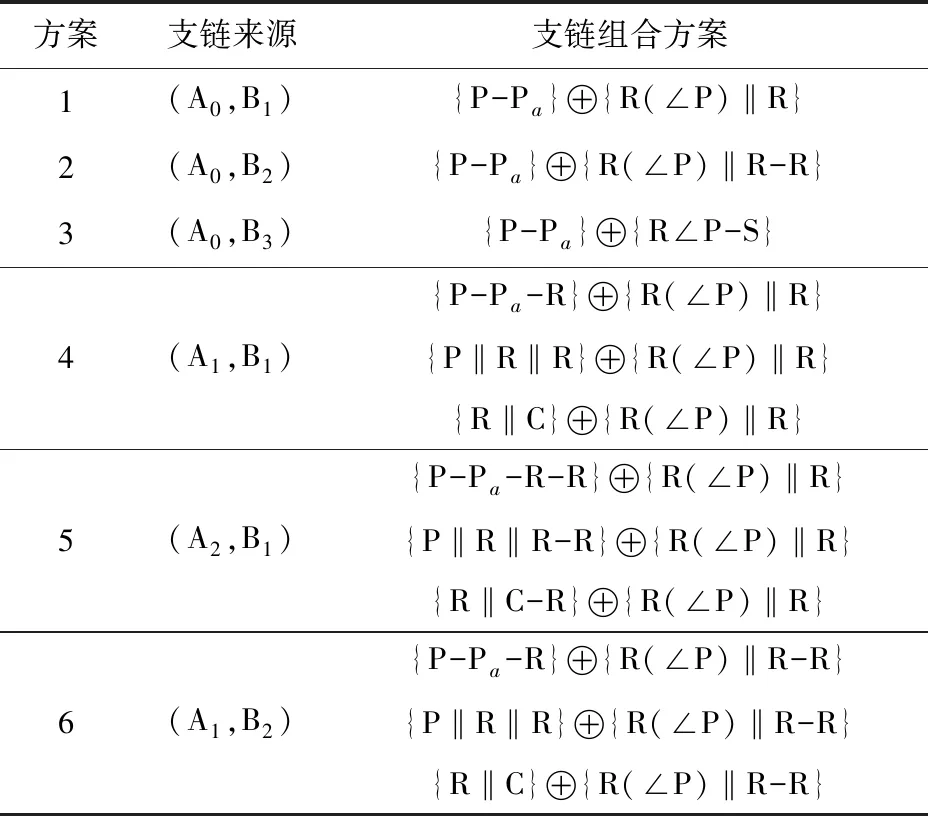
方案支鏈來源支鏈組合方案1(A0,B1){P-Pa}{R(∠P)‖R}2(A0,B2){P-Pa}{R(∠P)‖R-R}3(A0,B3){P-Pa}{R∠P-S}4(A1,B1){P-Pa-R}{R(∠P)‖R}{P‖R‖R}{R(∠P)‖R}{R‖C}{R(∠P)‖R}5(A2,B1){P-Pa-R-R}{R(∠P)‖R}{P‖R‖R-R}{R(∠P)‖R}{R‖C-R}{R(∠P)‖R}6(A1,B2){P-Pa-R}{R(∠P)‖R-R}{P‖R‖R}{R(∠P)‖R-R}{R‖C}{R(∠P)‖R-R}

(2)組合方案4。支鏈1取自表1中類型庫A1，支鏈2取自表4中類型庫B1，二者的轉動特征分別記為r1(R1)和r1(R2)。此時S1∩S2=?成立的充要條件為R1與R2不平行，因此支鏈1、2的裝配條件為R1與R2不平行。

(3)組合方案5和6。支鏈1、2分別取自類型庫A2和B1(或A1和B2)，二者的轉動特征可分別記為r1(R1,R2)和r1(R)，此時S1∩S2=?成立的條件為R與R1、R2均不平行。因此支鏈1、2的裝配條件為R與R1、R2均不平行。

3.3.4柱錐相貫線平移機構

根據3.3.2節得到的支鏈組合方案和裝配幾何條件，共可綜合得12種柱錐相貫線平移機構。圖7僅列舉了表4中各組合方案生成的部分代表性機構。根據自由度計算公式可計算得出，該類機構自由度為1。又由于兩支鏈末端構件轉動特征集的交集為空集，因此動平臺不含轉動輸出，僅能沿柱錐相貫線作平移運動。

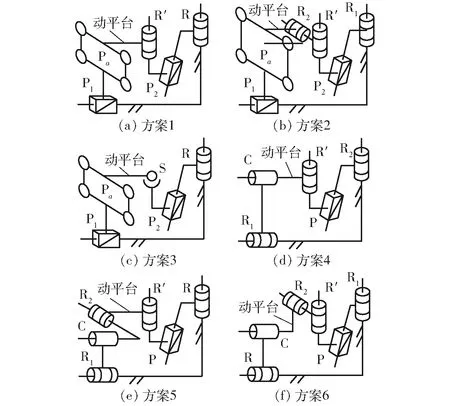
圖7 表4各組合方案生成的代表性并聯機構Fig.7 Representative mechanisms generated by assembling schemes in Tab.4

4 結論

(1)基于高斯非歐幾何的內蘊思想，可將曲線和曲面本身視為彎曲平移空間。這些空間的維數、整體形態以及生成方式能夠清晰表達末端構件的彎曲平移運動特征。

(2)支鏈末端構件的2維彎曲平移空間存在圓柱面(包括直圓柱面和斜圓柱面)、圓錐面、球面、環面4種基本類型。

(3)根據平移空間的整體形態，空間曲線平移機構可被劃分為9種基本類型。類型細分不僅能夠豐富和完善現有機構類型庫，而且有利于設計者根據實際工況作出合理選擇。

(4)綜合得到了25種柱柱相貫線平移機構和12種柱錐相貫線平移機構，并給出了代表性機構。與三平移機構相比，這些空間曲線平移機構具有自由度小(等于1)、結構簡單、控制容易等特點。