一個不可微算子的二步迭代法在ω條件下的半局部收斂分析*
徐秀斌, 何寧杰
(浙江師范大學 數學與計算機科學學院,浙江 金華 321004)
0 引 言
隨著科學技術的迅速發展,求解非線性算子方程在工程技術中已有廣泛的應用,但如可應用于非線性微分方程、邊值問題和積分方程組求解等領域是學術界關注的焦點.設X,Y是Banach空間,Ω?X是一非空開凸子集,H:Ω?X→Y為非線性算子,考慮求解非線性方程
H(x)=0.
(1)
一般情況下,通常用迭代法求解非線性方程(1)的根,如果H是一個可微算子,那么Newton法[1-4]就是解方程(1)最常用的迭代方法之一,其迭代格式為
xn+1=xn-[H′(xn)]-1H(xn),n=0,1,….
(2)
但是,這種方法需要算子H′的存在性,若算子H不可微,則無法使用Newton法解方程(1).在這種情況下,通常使用差商法去逼近Newton法中的算子H′(xn).記L(X,Y)為從X到Y的所有有界線性算子組成的空間,對x,y∈Ω,若[x,y;H]∈L(X,Y)滿足
[x,y;H](x-y)=H(x)-H(y),
(3)
則稱[x,y;H]為算子H在點x和y處的一階差商.
文獻[5]提出了與Newton法有相同收斂速度的線性插值法,且無需求解H′(xn),迭代格式如下:
(4)
文獻[6-8]把H拆成以下兩部分:
H(x)=F(x)+G(x)=0.
(5)
式(5)中:F是可微算子;G是連續不可微算子.
許多學者對Newton法作了二步修正[9-11],研究了半局部收斂性.文獻[12]提出了如下類似于二步修正Newton法的二步迭代法:
(6)
證明了在Lipschitz條件下的半局部收斂性.
文獻[13]引入了如下迭代法:
(7)
證明了該方法在一類ω條件下的半局部收斂性.
受文獻[12-13]的啟發,本文將討論迭代式(6)在ω條件下的半局部收斂性,同時證明解的唯一性.
1 半局部收斂性分析
這一節研究迭代法的半局部收斂性.取初值x0,y0∈Ω,并且假設:
1)‖y0-x0‖≤2α.
3)?x,y∈Ω,
‖F′(x)-F′(y)‖≤ω1(‖x-y‖).
(8)
式(8)中:ω1:R+→R+是一個連續不減的函數;ω(0)≥0.
4)?x,y,u,v∈Ω,
‖[x,y;G]-[u,v;G]‖≤ω2(‖x-u‖,‖y-v‖).
(9)
式(9)中:ω2:R+×R+→R+是關于2個變量都連續不減的函數;ω(0,0)≥0.
定理1假設條件1)~4)成立,記
m=max{β(ω1(η)+ω2(2α+η,0)),β(ω1(η)+ω2(2η,0))}.
不妨再設方程
(10)
存在最小正根r.如果


即x1∈B(x0,r).根據Taylor公式得

(11)
另一方面,由差商公式可知
G(x1)-G(x0)=[x1,x0;G](x1-x0).
(12)
結合式(11)和式(12)可知,
H(x1)=F(x1)+G(x1)=H(x0)+F′(x0)(x1-x0)+

-(F′(x0)+[y0,x0;G])(x1-x0)+F′(x0)(x1-x0)+

[x1,x0;G](x1-x0)-[y0,x0;G](x1-x0)+

(13)
從而
‖H(x1)‖≤‖[x1,x0;G]-[y0,x0;G]‖‖x1-x0‖+


(ω1(η)+ω2(2α+η,0))‖x1-x0‖.
(14)
又因為
所以
‖y1-x0‖≤‖y1-x1‖+‖x1-x0‖≤[1+β(ω1(η)+ω2(2α+η,0))]‖x1-x0‖ 即y1∈B(x0,r).由x1,y1∈B(x0,r)得 β(ω1(α+r)+ω2(2α+r,r))<1. (15) 即x2有定義. 由式(14)和式(15)可得 (16) 因此, ‖x2-x0‖≤‖x2-x1‖+‖x1-x0‖≤(M+1)‖x1-x0‖≤r, 即x2∈B(x0,r). 類似于式(13)可得 H(x2) =F(x2)+G(x2)=H(x1)+F′(x1)(x2-x1)+ -(F′(x1)+[y1,x1;G])(x2-x1)+F′(x1)(x2-x1)+ 從而 ‖H(x2)‖≤‖[x2,x1;G]-[y1,x1;G]‖‖x2-x1‖+ (ω1(η)+ω2(2η,0))‖x2-x1‖. (17) 所以 M‖x2-x1‖≤M2‖x1-x0‖; ‖y2-x0‖=‖y2-x2‖+‖x2-x1‖+‖x1-x0‖≤ M2‖x1-x0‖+M‖x1-x0‖+‖x1-x0‖≤(M2+M+1)‖x1-x0‖ 因此,y2∈B(x0,r). 假設xn,yn∈B(x0,r),則 β(ω1(α+r)+ω2(2α+r,r)) < 1. 所以Ln的逆存在,且 ‖xn+1-xn‖≤M‖xn-xn-1‖≤Mn‖x1-x0‖≤η. 類似于式(13)可得 H(xn) =F(xn)+G(xn)=H(xn-1)+F′(xn-1)(xn-xn-1)+ -(F′(xn-1)+[yn-1,xn-1;G])(xn-xn-1)+F′(xn-1)(xn-xn-1)+ [xn,xn-1;G](xn-xn-1)-[yn-1,xn-1;G](xn-xn-1)+ 從而 ‖H(xn)‖≤‖[xn,xn-1;G]-[yn-1,xn-1;G]‖‖xn-xn-1‖+ (ω1(η)+ω2(2η,0))‖xn-xn-1‖. 所以 M‖xn-xn-1‖≤Mn‖x1-x0‖. 那么 ‖xn+1-x0‖≤‖xn+1-xn‖+‖xn-xn-1‖+…+‖x1-x0‖≤ 故xn+1∈B(x0,r).從而證得由式(6)產生的序列{xn}是有定義的,且含于B(x0,r)中. 下證{xn}是柯西列.?q∈N,有 ‖xn+q-xn‖≤‖xn+q-xn+q-1‖+‖xn+q-1-xn+q-2‖+…+‖xn+1-xn‖≤ (18) ‖H(xn)‖≤(ω1(r)+ω2(2r,0))‖xn-xn-1‖, 所以當n→∞時,‖xn-xn-1‖→0.由H(x)的連續性可知,H(x*)=0. 則 L(y*-x*)=H(y*)-H(x*)=0. 因此,如果L-1存在,那么必有y*=x*.實際上, βω2(‖y*-y0‖,‖x*-x0‖)≤β(ω1(r)+ω2(r+2α,r))<1. 由Banach引理可知,L-1存在,故y*=x*.定理1證畢. 考慮條件3)和4)的特殊情形: 3′)?x,y∈Ω, ‖F′(x)-F′(y)‖≤K‖x-y‖,K>0. 4′)?x,y,u,v∈Ω, ‖[x,u;G]-[y,v;G]‖≤K‖x-y‖+K‖u-v‖,K>0. 則得 推論1在1),2),3′)和4′)成立的條件下,設m=max{βK(2α+2η),3Kβη}.假設方程 考慮下列非線性方程組: (19) 式(19)中,(x1,x2)∈Ω:={(x1,x2)∈R2|x1,x2>0}.令 F=(f1,f2),G=(g1,g2). 易知 因此, α≈0.116 5;β≈0.753 6;η≈0.230 4;m≈0.341 1;r≈0.500 3. 且β(ω1(α+r)+ω2(2α+r,r))≈0.632 2<1,M≈0.927 4<1.從而滿足了半局部收斂結果的假設,解的唯一性區域為{x∈R2:‖x-x0‖≤0.500 3}. 討論了具有不可微算子的二步迭代法的半局部收斂性,證明了非線性算子F的一階導數和非線性算子G的一階差商滿足ω條件下的半局部收斂定理,推廣了文獻[12]的結果.但本文未給出不可微算子的二步迭代法在ω條件下的局部收斂定理及收斂半徑,這是以后還可以繼續研究的課題.











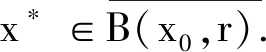





2 數值例子

3 結 語

