零膨脹模型在散裝熟肉制品中單核細(xì)胞增生李斯特氏菌定量暴露評估中的應(yīng)用
孫菀霞,金玉琴,戴穎秀,肖建偉,王 翔,董慶利,*
(1.上海理工大學(xué)醫(yī)療器械與食品學(xué)院,上海 200093;2.上海市楊浦區(qū)疾病預(yù)防控制中心,上海 200090)
單核細(xì)胞增生李斯特氏菌(Listeria monocytogenes,以下簡稱單增李斯特菌)是一種能夠引起人畜共患病的致病菌,廣泛分布于自然界,如土壤、污水、人和動物糞便以及多種食品中。由單增李斯特菌導(dǎo)致的李斯特菌病通常發(fā)病率低但后果嚴(yán)重,該菌可穿透腸道、血腦和胎盤三大屏障,引起人類腹瀉、腦膜炎、敗血癥等疾病[1-2],人類一旦感染死亡率高達(dá)20%~30%[3-4]。易感人群主要包括老年人、免疫功能缺陷者、孕婦及新生兒[5]。已有資料表明,單增李斯特菌的發(fā)病與即食食品有較大關(guān)系[6]。我國污染物監(jiān)測網(wǎng)2010—2013年的資料[7-9]顯示,我國的即食涼拌菜、熟肉制品、生食水產(chǎn)品和豆制品均受到單增李斯特菌不同程度的污染,在對上述各類即食食品中單增李斯特菌的暴露情況進(jìn)行初步風(fēng)險分級和比較之后,散裝熟肉制品被認(rèn)為可能是導(dǎo)致我國居民發(fā)生食源性李斯特菌病的主要食品類別之一。因此,對散裝熟肉制品中單增李斯特菌進(jìn)行定量風(fēng)險評估對減少食源性李斯特菌病的發(fā)生、保障消費者健康以及減輕國家經(jīng)濟負(fù)擔(dān)具有一定意義。
1999年食品法典委員會制定的《微生物風(fēng)險評估原則和指導(dǎo)方針》將微生物定量風(fēng)險評估分為危害識別、危害特征描述、暴露評估和風(fēng)險特征描述4 個步驟[10]。暴露評估作為風(fēng)險評估的核心內(nèi)容,其主要作用是在統(tǒng)計分布的基礎(chǔ)上對某個個體或群體暴露于致病菌的可能性及攝入的菌量進(jìn)行估計[11-12]。進(jìn)行暴露評估時,常用泊松分布描述菌落計數(shù)過程中的隨機性,用對數(shù)正態(tài)分布描述致病菌的濃度[13-14]。當(dāng)同時考慮計數(shù)隨機性和污染水平變異性時,采用負(fù)二項分布或泊松對數(shù)正態(tài)分布進(jìn)行描述[15-16]。在實際檢測中,受檢測方法所限,無法完全定量樣品中已存在的微量致病菌,當(dāng)致病菌的含量小于定量檢測限(limit of quantification,LOQ)時就會產(chǎn)生左刪失數(shù)據(jù)[17]。此類數(shù)據(jù)實際上是由“陰性樣本”(真零值)和“假陰性樣本”(非零值)兩個部分共同構(gòu)成,并通常均以“<LOQ”的形式表達(dá)。目前,在微生物定量暴露評估中,針對左刪失數(shù)據(jù)的常用處理方法是將缺失的數(shù)據(jù)以某種特定分布的形式代替[18-20]。然而,對于散裝熟肉制品中的單增李斯特菌而言,監(jiān)測結(jié)果中的左刪失數(shù)據(jù)通常占據(jù)較大比例,并且包含大量的真零值,數(shù)據(jù)呈現(xiàn)出零膨脹現(xiàn)象[21],超出了傳統(tǒng)模型所能估計的范疇,造成實際數(shù)據(jù)與既定的傳統(tǒng)模型之間可能存在較大偏離,導(dǎo)致暴露評估結(jié)果不準(zhǔn)確。另外,在單增李斯特菌的監(jiān)測結(jié)果中除了零膨脹現(xiàn)象外,還常常出現(xiàn)過度離散的現(xiàn)象。若忽視這一現(xiàn)象也將導(dǎo)致不準(zhǔn)確的暴露評估結(jié)果。
因此,本研究以上海市某區(qū)散裝熟肉制品中單增李斯特菌的定量檢測結(jié)果為例,探究不同概率分布的選擇對暴露評估結(jié)果的影響,以期提供較為理想的左刪失數(shù)據(jù)處理方法,提高風(fēng)險評估結(jié)果的準(zhǔn)確性,同時為風(fēng)險管理提供可靠的理論依據(jù)。
1 材料與方法
1.1 散裝熟肉制品中單增李斯特菌的定量檢測
2017年2—12月從上海市某區(qū)各大超市、農(nóng)貿(mào)市場以及餐飲環(huán)節(jié)隨機采集散裝熟肉制品共254 份,每份樣品250 g(表1)。根據(jù)GB 4789.30—2016《食品安全國家標(biāo)準(zhǔn) 食品微生物學(xué)檢驗 單核細(xì)胞增生李斯特氏菌檢驗》進(jìn)行單增李斯特菌定量檢測,并參照單增李斯特菌最可能數(shù)(most probable number,MPN)檢索表獲得單增李斯特菌濃度[22]。采集的樣品均置于干冰貯存箱內(nèi)轉(zhuǎn)運至實驗室進(jìn)行檢測,檢測結(jié)果可近似認(rèn)為是零售階段散裝熟肉制品中單增李斯特菌的污染水平。

表1 2017年上海市某區(qū)不同時間散裝熟肉制品的采樣地點、采樣量及單增李斯特菌定量檢測結(jié)果Table 1 Sampling locations, number of samples and number of samples positive for L. monocytogenes in bulk cooked meat products in a certain district of Shanghai in 2017
1.2 模型構(gòu)建
根據(jù)254 份樣品中單增李斯特菌的定量檢測結(jié)果,分別選用泊松分布、負(fù)二項分布、對數(shù)正態(tài)分布、泊松對數(shù)正態(tài)分布及其零膨脹形式進(jìn)行擬合,從而定量描述零售階段散裝熟肉制品中單增李斯特菌的污染水平。
1.2.1 標(biāo)準(zhǔn)統(tǒng)計分布
1.2.1.1 泊松分布
假設(shè)254 份散裝熟肉制品中單增李斯特菌的數(shù)量服從泊松分布(平均值等于方差),則其概率質(zhì)量函數(shù)如式(1)[23]所示。

式中:Yi表示散裝熟肉制品中單增李斯特菌的定量檢測結(jié)果;λ表示樣本數(shù)據(jù)的平均值;Pr(Yi)為單增李斯特菌的概率質(zhì)量。
1.2.1.2 負(fù)二項分布
當(dāng)單增李斯特菌的檢測結(jié)果出現(xiàn)過度離散現(xiàn)象時,常用負(fù)二項分布取代泊松分布進(jìn)行描述,其概率質(zhì)量函數(shù)如式(2)[23]所示。
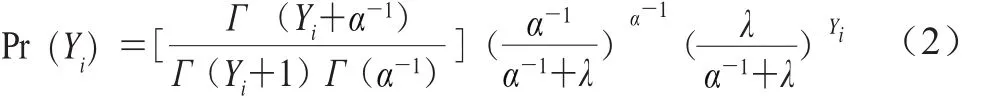
式中:α表示離散參數(shù);Yi表示單增李斯特菌的定量檢測結(jié)果;Γ表示伽馬函數(shù),即Γ(α)=∫∞0e-ttα-1dt;Pr(Yi)為單增李斯特菌的概率質(zhì)量。
1.2.1.3 對數(shù)正態(tài)分布
對數(shù)正態(tài)分布作為一種連續(xù)型分布,可以對單增李斯特菌的濃度結(jié)果進(jìn)行描述。當(dāng)零膨脹數(shù)據(jù)過多時,該分布的估計值與實際值之間可能有較大偏離,其概率密度如式(3)所示。
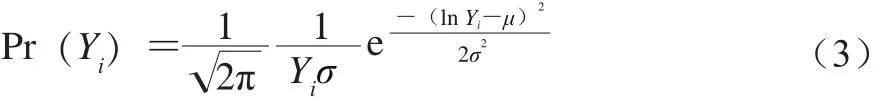
式中:Yi表示單增李斯特菌的污染濃度;μ和σ分別為定量檢測結(jié)果的對數(shù)平均值和對數(shù)方差;Pr(Yi)為單增李斯特菌的概率密度。
1.2.1.4 泊松對數(shù)正態(tài)分布
統(tǒng)計學(xué)上,針對過度離散現(xiàn)象常用的處理方法是進(jìn)行對數(shù)轉(zhuǎn)換。本研究選擇泊松對數(shù)正態(tài)分布描述不同樣本之間單增李斯特菌數(shù)量的變異性和不確定性,其概率質(zhì)量函數(shù)如式(4)所示。

式中:Yi表示單增李斯特菌定量檢測結(jié)果的對數(shù)值;λ服從對數(shù)正態(tài)分布,即λ~Lognormal(μ,σ);Pr(Yi)為單增李斯特菌的概率質(zhì)量。
1.2.2 零膨脹統(tǒng)計分布
零膨脹分布中小于LOQ的數(shù)值來源于兩種不同的過程:一種是由于樣本未被污染而表現(xiàn)出的真零值,其真零值的待估計概率用p0表示;另一種是由于檢測方法所限導(dǎo)致未檢出的數(shù)值。
1.2.2.1 零膨脹泊松分布
若散裝熟肉制品中單增李斯特菌的定量檢測結(jié)果出現(xiàn)零膨脹現(xiàn)象,且陽性數(shù)據(jù)服從泊松分布,則可采用零膨脹泊松分布進(jìn)行描述,具體如式(5)所示。

式中:p0為“零膨脹參數(shù)”,表示真零值的概率;Yi表示單增李斯特菌的定量檢測結(jié)果;λ表示樣本數(shù)據(jù)的平均值;Pr(Yi)為單增李斯特菌的概率質(zhì)量。
1.2.2.2 零膨脹負(fù)二項分布
若單增李斯特菌的陽性檢測結(jié)果出現(xiàn)偏大離差(方差大于期望),則需要將零膨脹泊松分布擴展到零膨脹負(fù)二項分布,其概率質(zhì)量函數(shù)如式(6)所示。
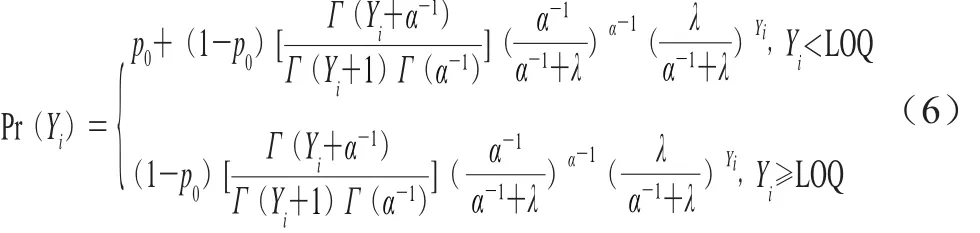
式中:p0為陰性樣本的待估計概率;α表示離散參數(shù);Yi表示單增李斯特菌的定量檢測結(jié)果;Pr(Yi)為單增李斯特菌的概率質(zhì)量。
1.2.2.3 零膨脹對數(shù)正態(tài)分布
零膨脹對數(shù)正態(tài)分布概率密度函數(shù)如式(7)所示。
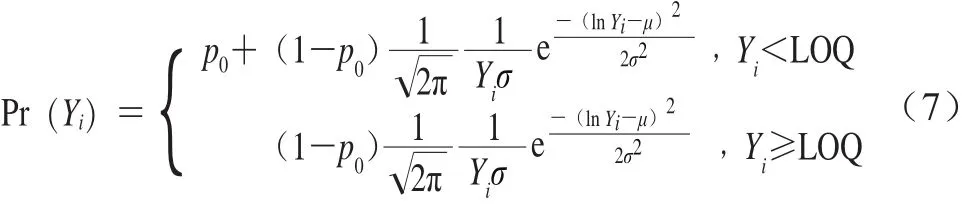
式中:p0為陰性樣本所占的比例;Yi表示單增李斯特菌的污染濃度;μ和σ分別為定量檢測結(jié)果的對數(shù)平均值和對數(shù)方差;Pr(Yi)為單增李斯特菌的概率密度。
1.2.2.4 零膨脹泊松對數(shù)正態(tài)分布
為盡可能縮小樣本檢測結(jié)果的離散程度,本研究選擇采用泊松對數(shù)正態(tài)分布描述陽性樣本間的變異性和不確定性,其零膨脹形式的概率質(zhì)量函數(shù)如式(8)所示。
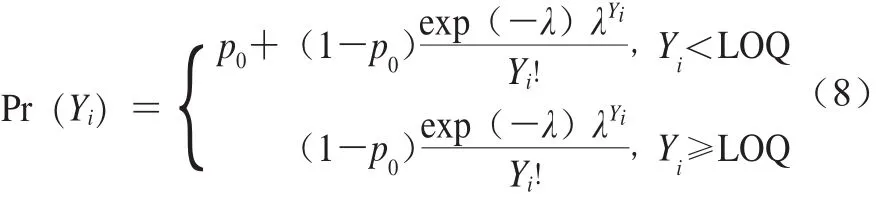
式中:p0為陰性樣本的檢出率;Yi表示單增李斯特菌的定量檢測結(jié)果的對數(shù)值;λ服從對數(shù)正態(tài)分布;Pr(Yi)為單增李斯特菌的概率質(zhì)量。
1.3 參數(shù)估計
標(biāo)準(zhǔn)統(tǒng)計分布與零膨脹分布的參數(shù)估計均可采用最大似然估計的方法。在進(jìn)行參數(shù)估計時,泊松分布與泊松對數(shù)正態(tài)分布的差異在于是否進(jìn)行模型參數(shù)λ的對數(shù)轉(zhuǎn)換,即λ的數(shù)值不同,因此本研究只給出泊松分布和零膨脹泊松分布似然函數(shù)的顯式。本節(jié)模型中模型參數(shù)的意義與1.2節(jié)相同。泊松分布、負(fù)二項分布、對數(shù)正態(tài)分布及其零膨脹模型的對數(shù)似然函數(shù)分別如式(9)~(14)所示。
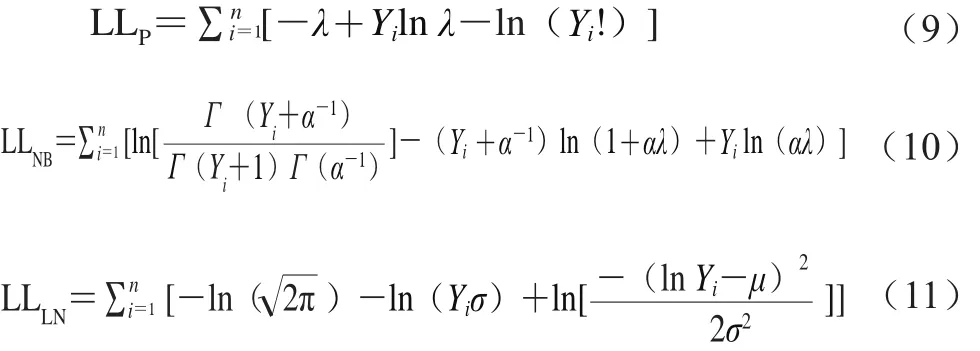
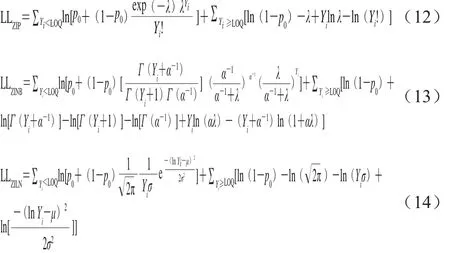
式中:LLP、LLNB和LLLN分別為泊松分布、負(fù)二項分布和對數(shù)正態(tài)分布的對數(shù)似然函數(shù);LLZIP、LLZINB和LLZILN別為零膨脹泊松分布、零膨脹負(fù)二項分布和零膨脹對數(shù)正態(tài)分布的對數(shù)似然函數(shù)。
1.4 模型選擇
在不考慮模型間關(guān)系的前提下,通過信息準(zhǔn)則指標(biāo)進(jìn)行模型的選擇與比較。本研究選用被廣泛用于判斷模型優(yōu)劣的赤池信息準(zhǔn)則(Akaike information criterion,AIC)、貝葉斯信息準(zhǔn)則(Bayesian information criterion,BIC)[24]。通過對每個模型計算AIC、BIC值并比較其大小,從而完成對模型的選擇。模型評價參數(shù)公式如式(15)、(16)[25]所示。

式中:LL表示模型對數(shù)似然函數(shù)的最大值;k1和k2分別為模型種參數(shù)的個數(shù);n為樣本量。AIC和BIC值遵循取值越小模型越優(yōu)的原則。
X2統(tǒng)計量是對于數(shù)據(jù)的分布與預(yù)期(或假設(shè))分布之間差異的度量,因此,利用卡方統(tǒng)計量比較各個模型的優(yōu)劣,如公式(17)[25]所示。

式中:k為總體被分成數(shù)據(jù)段的個數(shù);Ni為第i個數(shù)據(jù)段中觀測的樣本數(shù);Ei為第i個數(shù)據(jù)段中期望的樣本數(shù)。
2 結(jié)果與分析
2.1 散裝熟肉制品中單增李斯特菌的定量檢測結(jié)果
采集254 份散裝熟肉制品進(jìn)行單增李斯特菌定量檢測,陽性樣品的檢出時間及檢出地點如表1所示。40 份大型超市散裝熟肉樣品中均未出現(xiàn)單增李斯特菌陽性檢測結(jié)果。農(nóng)貿(mào)市場和餐飲環(huán)節(jié)共檢出4 份陽性樣品。總體陽性檢出率為1.57%,由此可見,小于LOQ的樣本量占據(jù)較大比例,出現(xiàn)了零膨脹現(xiàn)象。
由表2可知,4 份陽性樣品中單增李斯特菌濃度的最小值和最大值分別為3.6 MPN/g和75.0 MPN/g,平均值為22.85 MPN/g,方差為1 215.69,單增李斯特菌陽性檢出結(jié)果出現(xiàn)偏大離差現(xiàn)象。

表2 2017年上海市某區(qū)散裝熟肉制品中單增李斯特菌抽樣調(diào)查的陽性檢測結(jié)果Table 2 Quantification of L. monocytogenes in bulk cooked meat samples in a certain district of Shanghai in 2017
2.2 零售階段散裝熟肉制品中單增李斯特菌的污染水平
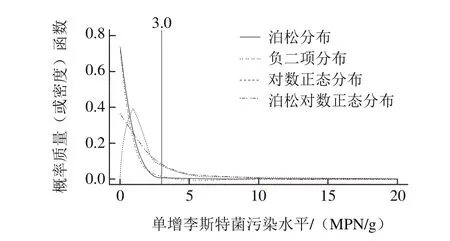
圖1 泊松分布、負(fù)二項分布、對數(shù)正態(tài)分布和泊松對數(shù)正態(tài)分布擬合單增李斯特菌定量檢測數(shù)據(jù)的概率質(zhì)量(或密度)Fig. 1 Predictive distribution of the L. monocytogenes contamination level as modeled by the Poisson, Negative Binomial, Lognormal and Poisson Lognormal models
如圖1所示,與對數(shù)正態(tài)分布和泊松對數(shù)正態(tài)分布相比,泊松分布和負(fù)二項分布有較高的預(yù)測零值。進(jìn)行了對數(shù)轉(zhuǎn)換的標(biāo)準(zhǔn)統(tǒng)計分布所估計的陽性樣本污染濃度較高,且陽性率的估計值也高于泊松分布和負(fù)二項分布。
對單增李斯特菌污染水平進(jìn)行擬合時,由于對數(shù)正態(tài)分布在零處無意義,因此,與其他標(biāo)準(zhǔn)統(tǒng)計分布估計的零值概率產(chǎn)生較大差異。由此可見,標(biāo)準(zhǔn)對數(shù)正態(tài)分布不適于估計低菌量條件下的污染水平。Gonzales-Barron等[26]利用對數(shù)轉(zhuǎn)換方法對牛胴體表面的大腸桿菌進(jìn)行濃度估計時也得到相似的結(jié)論。

圖2 零膨脹模型擬合單增李斯特菌濃度的累積概率Fig. 2 Cumulative probability of L. monocytogenes MPN results as fitted by zero-inflated distribution
圖2描述了4 種零膨脹模型的累積概率,結(jié)果表明零膨脹模型比標(biāo)準(zhǔn)統(tǒng)計分布有更高的預(yù)測零值。零膨脹對數(shù)正態(tài)分布克服了其標(biāo)準(zhǔn)形式的不足,與帶有層次結(jié)構(gòu)的零膨脹泊松對數(shù)正態(tài)分布得到的擬合結(jié)果相似。相比于零膨脹對數(shù)正態(tài)分布和零膨脹泊松對數(shù)正態(tài)分布,零膨脹負(fù)二項分布在一定程度上低估了單增李斯特菌的污染水平。
零膨脹泊松分布與其他零膨脹模型的累積概率產(chǎn)生較大差異,主要是因為該組數(shù)據(jù)的陽性檢測結(jié)果有偏大離差現(xiàn)象,而泊松分布只適用于擬合平均值等于方差的數(shù)據(jù)[27]。根據(jù)模型擬合結(jié)果可以推斷,4 種零膨脹模型均可以對左刪失數(shù)據(jù)的零膨脹現(xiàn)象進(jìn)行準(zhǔn)確的估計。
2.3 模型參數(shù)與模型比較
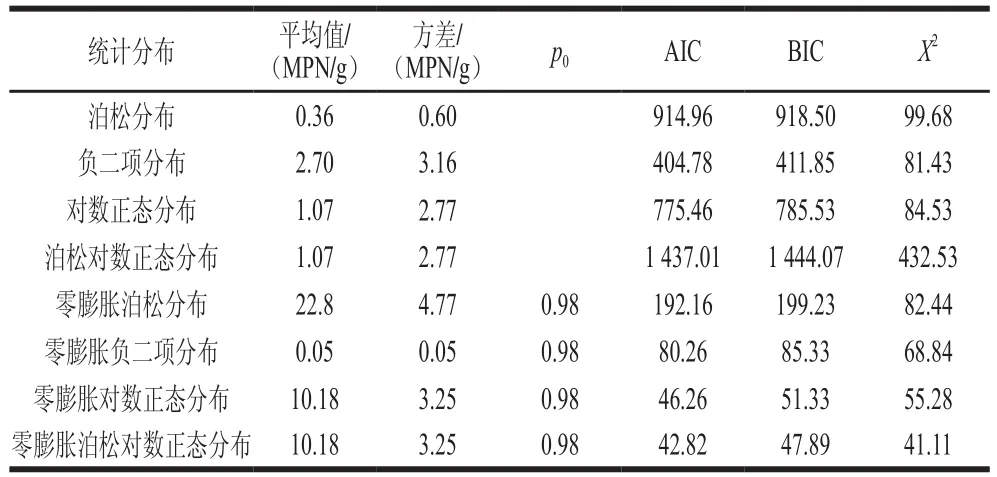
表3 基于散裝熟肉制品中單增李斯特菌定量檢測數(shù)據(jù)的參數(shù)估計Table 3 Model parameter estimates based on quantitative detection of L. monocytogenes in bulk cooked meat products
泊松分布、負(fù)二項分布、對數(shù)正態(tài)分布、泊松對數(shù)正態(tài)分布及其零膨脹模型的參數(shù)估計及擬合效果見表3。零膨脹參數(shù)p0顯著不為零,這進(jìn)一步說明散裝熟肉制品中單增李斯特菌呈現(xiàn)零膨脹現(xiàn)象,同時也表明標(biāo)準(zhǔn)統(tǒng)計分布均不適合描述該組數(shù)據(jù)。另外,由模型評價結(jié)果可知,零膨脹泊松對數(shù)正態(tài)分布比其他零膨脹模型更適合擬合該組數(shù)據(jù),說明單增李斯特菌的陽性污染水平出現(xiàn)偏大離差。
參照GB 29921—2013《食品安全國家標(biāo)準(zhǔn) 食品中致病菌限量》[28]規(guī)定的預(yù)包裝熟肉制品中單增李斯特菌限量標(biāo)準(zhǔn),同時出于保護(hù)消費者健康的角度考慮,本研究將散裝熟肉制品中單增李斯特菌的風(fēng)險閾值設(shè)定為不得檢出(每份樣品25 g)。由表3可以看出,零膨脹模型所估計的總體陽性檢出率均為2%,這與實際監(jiān)測的陽性率(1.57%)接近。
3 討 論
本研究基于散裝熟肉制品中單增李斯特菌的定量檢測結(jié)果構(gòu)建零膨脹模型,并與傳統(tǒng)模型進(jìn)行比較,將擬合結(jié)果應(yīng)用于單增李斯特菌的暴露評估中,為食源性致病菌檢測數(shù)據(jù)中出現(xiàn)的零膨脹和過度離散現(xiàn)象提供方法學(xué)支持。
研究發(fā)現(xiàn),盡管泊松分布常作為描述食源性致病菌污染水平的假設(shè)統(tǒng)計分布之一,但是它對數(shù)據(jù)有著嚴(yán)格的要求[29-30],因此并不能較好地處理檢測結(jié)果之間的變異性。一般來說,當(dāng)單增李斯特菌的檢測結(jié)果出現(xiàn)由較大變異性所導(dǎo)致的過度離散現(xiàn)象時,通常可以采用負(fù)二項分布和對數(shù)正態(tài)分布分別對菌落計數(shù)和污染濃度進(jìn)行擬合[31]。然而,當(dāng)數(shù)據(jù)中存在由零膨脹現(xiàn)象導(dǎo)致的過度離散現(xiàn)象時,則需要采用能夠準(zhǔn)確描述陽性樣本變異性的零膨脹模型進(jìn)行擬合。此時若依然選擇標(biāo)準(zhǔn)統(tǒng)計分布進(jìn)行單增李斯特菌的定量暴露評估,不但會低估真實零值的概率,而且對于陽性樣本污染濃度較高的情況也無法作出準(zhǔn)確估計。
通過分析不同模型對散裝熟肉制品中單增李斯特菌暴露水平的描述情況,可以看出:1)零膨脹模型處理左刪失數(shù)據(jù)的能力明顯優(yōu)于標(biāo)準(zhǔn)統(tǒng)計分布;2)零膨脹模型可以同時估計陽性率和陽性樣本的污染水平;3)零膨脹模型污染濃度的參數(shù)估計值受LOQ影響小。因此,在進(jìn)行暴露評估時,建議優(yōu)先選擇零膨脹模型。另外,本研究無法區(qū)分零膨脹對數(shù)正態(tài)分布與零膨脹泊松對數(shù)正態(tài)分布的優(yōu)劣。本研究中的擬合優(yōu)度指標(biāo)雖然顯示零膨脹泊松對數(shù)正態(tài)分布優(yōu)于零膨脹對數(shù)正態(tài)分布,但是二者之間的差距不大。因此,在進(jìn)行模型選擇時需更注重數(shù)據(jù)類型(離散變量或連續(xù)變量)及數(shù)據(jù)結(jié)構(gòu)(零值的比例及來源)。

