非承壓含水層底部單孔疏放水滲流特征
李 洋,王文學,肖 航,孫 毅,王 運,狄夢娜
?
非承壓含水層底部單孔疏放水滲流特征
李 洋1,王文學2,肖 航1,孫 毅3,王 運3,狄夢娜3
(1. 河南省水文水資源局,河南 鄭州 450003;2. 華北水利水電大學,河南省巖土力學與結構工程重點實驗室,河南 鄭州 450045;3. 河南省地礦建設工程(集團)有限公司,河南 鄭州 450007)
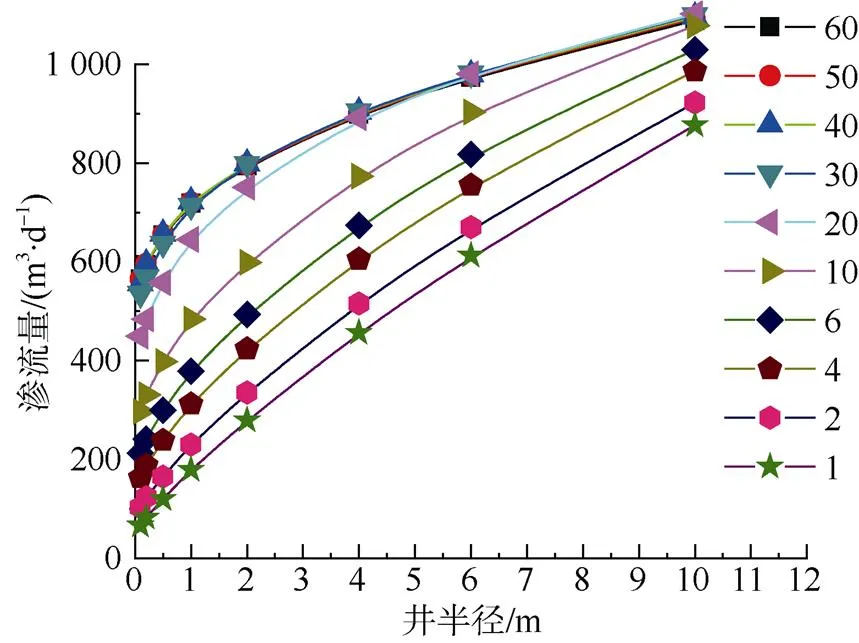
由含水層底部向上施工疏放水孔(井)進行疏水降壓是保證煤礦安全開采的重要措施之一,該類疏放水孔與地面抽水井的滲流特征具有顯著差別。為了研究井下疏放水孔的滲流特征,以非承壓含水層底部單井疏放水孔為例,采用數值模擬的方法對其滲流特征進行研究。研究結果表明,當疏放水井的井長w小于臨界長度c時,即w 含水層;疏放水井;涌水量;Dupuit公式 水體(含水層、水庫、河流、湖、海等)下煤層開采在國內外煤炭工業生產中普遍存在[1-5]。地下煤層開采導致上覆巖層垮落、沉降變形,采動裂隙由下而上擴展,形成大量滲流通道,一旦裂隙導入上覆含水層(體),將引起工作面涌水量增大或突水,對安全施工構成威脅。預測預防突水及準確預測涌水量對地下工程安全施工尤為重要。 超前探測并對含水層(體)進行疏水降壓是解決水體下工程施工發生突水潰砂災害的有效手段[6-7]。對于深部地下工程施工,地面施工鉆孔進行抽排水降壓,時間長、費用高,在地下空間施工仰斜鉆孔對含水層(體)進行疏水降壓更為經濟、合理[8]。此外,采動裂隙向上發育揭穿含水層的長度以及面積對工作面涌水量影響顯著,以往多采用“大井法”對工作面的涌水量進行計算[9-10],將裂隙揭穿含水層區域看作同面積的大井,采用裘布衣(Dupuit)完整井公式計算。因此,研究含水層底部仰斜鉆孔的滲流特征對如何更有效地施工井下疏放水孔以及準確預測礦井涌水量具有重要的指導意義。 在井下探放水鉆孔涌水量計算方面,李明山等[11]從水力學中的伯努利(Bernoulli)方程出發, 考慮水流的水頭損失, 推導出一種井下探放水鉆孔涌水量計算的新方法;陳實等[12]以空間點源理論為基礎,運用反映法,建立了均質各向異性無限水平承壓含水層中非完整傾斜鉆孔的井流計算方程,討論了多個傾斜鉆孔同時工作時,多孔疊加的疏放水井流計算方法;趙寶峰[13]通過灰色關聯度計算和對各影響因素與疏放水量之間關聯度的比較,鉆孔方位角對鉆孔疏放水量影響最大,含水層厚度、鉆孔仰角、孔深對鉆孔疏放水量影響依次減小,并指出只要鉆孔穿透有效含水層即可,過長的孔深不會有效的增加疏放水量;靳月燦等[14]應用有限厚度的承壓非完整井理論,對某礦收縮開采階段中封閉不良防塵取水孔的涌水量預測進行了討論。上述研究在井下疏放水鉆孔計算滲流量方面取得一定進展,但井下疏放水孔與地面抽水井滲流特征存在明顯差別,井下疏放水鉆孔由含水層底部進入,鉆孔進入含水層的長度、鉆孔半徑對滲流量的定量影響仍不清楚。 筆者考慮疏放水孔半徑、長度的影響,借助于數值模擬軟件Midas GTS NX滲流分析,采用數值模擬的方法研究含水層底部施工疏放水孔滲流特征,為了便于研究將井下疏放水井視為垂直鉆孔,研究疏放水孔進入含水層的長度、半徑對其涌水量的影響,對井下疏放水孔的施工及滲流量的計算提供理論基礎。 a.含水層水平分布,等厚均勻、各向同性; b. 含水層頂底板無垂向補給、排泄; c. 滲流滿足達西定律; d.滲流井傾角90°,井壁及井底均可進水; e.滲流井內壓力水頭為0。 Midas GTS NX是一款針對巖土領域研發的通用有限元分析軟件,支持線性或非線性動態分析、滲流和固結分析、邊坡穩定分析、施工階段分析等多種分析類型,可以進行滲流–應力耦合、滲流–邊坡耦合等多種耦合分析。 模型中含水層在,和方向上的尺寸分別為1 200、1 200、60 m,在模型中間設置疏放水井,疏放水井由含水層底板中心點向上施工,含水層邊界為定水頭邊界。模型垂直方向厚度為60 m,將含水層邊界總水頭設為60 m,即整個含水層內充滿水,但不承壓,滲流井井壁及井底均可向井內滲流,流入井內水被及時排出,不存水,本次研究中不考慮滲出面(水躍)問題,井壁及井底內外壓力水頭為0,含水層滲透系數為0.4 m/d。 為了分析疏放水井井徑的影響,本次模型中將井徑設定為0.1、0.2、0.5、1、2、4、6、10 m,井長由含水層底部向上以1 m為間隔逐漸增加至含水層頂部以分析井長對滲流的影響,具體數值模擬模型如圖1所示。 在無限延伸潛水含水層中單井完整井抽水穩定流滲流量計算公式如式(1)所示,在數值模擬分析過程中,井長與含水層厚度相等時,疏放水井為完整井,此時,可以采用潛水完整井公式(1)計算疏放水井的滲流量,不同井徑疏放水完整井數值模擬滲流量及采用Dupuit潛水完整井穩定流計算公式的計算結果如表1和圖2所示。可以看出,不同井徑疏放水完整井采用Dupuit潛水完整井穩定流計算公式與數值模擬結果吻合較好,最大誤差小于8.24%,說明數值模型模擬結果可靠。 式中為抽水井流量,m3/d;為滲透系數,m/d;為抽水井中水位降深,m;0為潛水含水層天然厚度,m;w為抽水井半徑,m;為影響半徑,m。 圖2 疏放水井不同井徑滲流量理論計算與數值模擬結果對比 以往的研究認為由含水層底部向上鉆取疏放水井的涌水量與鉆入含水層的長度無關或者在計算涌水量時可不考慮鉆孔鉆入含水層的長度。但研究發現,當疏放水井的半徑及長度均較小時,疏放水井上方含水層內的孔隙水壓力仍大于0,疏放水孔上方的水不能完全滲流入疏放水井,以半徑為1.0 m時不同井長的穩定滲流流網為例,如圖3所示。 圖3 不同井長穩定滲流條件下等水位及流網分布(Rw=1.0 m) 在疏放水井井底上方附近會形成等勢線降低區,等勢線以滲流井為中心呈“拱形”向外圍逐漸擴展。“拱形”等勢線隨著滲流井長的增加其中間圓弧曲率逐漸增加,中間凸起越明顯。當“拱形”等勢線擴展至地下水水位線時,“拱形”等勢線在滲流井兩側轉變為兩條分開的等勢線曲線。滲流井兩側分開的等勢線曲線在水平方向隨著距疏放水井距離增加其等勢線所代表的值越大,如圖3所示。圖3中,兩條等勢線間的水頭差值為5 m,圖中只顯示水平方向距離井心50 m范圍等勢線分布特征。滲流井周圍流線在含水層底部曲率最小,在滲流井中心上方,流線曲率最大。滲流井上方流線曲率隨著滲流井井長的增加,逐漸減小,當滲流井井長達到地下水水位線以上時,此時的疏放水井上方流線曲率最小,且不再隨著井長的增加而變化。 圖4 不同井長穩定滲流條件下孔隙水壓力分布曲線(Rw=1.0 m) 當地下水位降低至疏放水井長以下時,疏放水井的等勢線及流線不再隨著井長的增加變化,此時,井底上方孔隙水壓力降低為0(本次研究不考慮非飽和土效應)。 疏放水井周圍孔隙水壓分布特征如圖4所示。當疏放水井的半徑及長度均較小時,疏放水井上方含水層內的孔隙水壓力仍大于0,疏放水孔上方的水不能完全滲流入疏放水井。在疏放水井井底上方附近會形成孔隙水壓力降低區,在水平方向隨著距疏放水井中心距離增加,孔隙水壓力逐漸增加至初始孔隙水壓力。 井底上方孔隙水壓力降低區及孔隙水壓力為0的范圍隨著井長的增加而增加,當井長增大到一定程度后,孔隙水壓力降低區的范圍不再隨著井長的增加而改變,在井長1 m至60 m數值模擬中,分析發現當井長大于33 m時(該模型流網與圖3中井長40、50、60 m相同),疏放水井引起含水層孔隙水壓力變化曲線基本穩定,不再隨著井長的增加而改變;當疏放水井的井長較小時,如井長小于33 m時,疏放水井底上方含水層內孔隙水壓力大于0,由井底向上形成孔隙水壓力先增加再減小的規律,距離井底較遠位置孔隙水壓力由下而上逐漸減小,如圖4和圖5所示。圖5為井徑1.0 m、井長10 m時,疏放水井中心上方及水平方向距疏放水井中心10 m位置的孔隙水壓力由下而上的變化,可以看出在疏放水井中心上方孔隙水壓力水頭由0逐漸增加至20 m,然后逐漸減小至0;而水平方向距離疏放水井10 m位置孔隙水壓力由下而上由40 m逐漸變為0。 圖5 疏放水井中心上方及水平距離10 m位置垂直方向孔隙水壓力分布(Rw=1.0 m, lw=10 m) 對于地下煤層開采,無論在地面還是井下施工鉆孔進行疏放水,合理的布設疏放水井尤為重要,即最少的鉆進長度達到最優的疏放水效果[15]。對于井下疏放水鉆孔,除合理布設其鉆井位置,單個疏放水孔的鉆進參數,例如井長、井徑,也顯著影響疏放水效果。 不同半徑的疏放水井滲流量與井長的關系如圖6所示,可以看出在初始階段,隨著井長的增加,滲流量也在增加,通過擬合發現滲流量與井長滿足=+exp(w)(2>0.99)指數函數關系,、和均為擬合參數。當井長超過臨界長度c時滲流量達到最大,且不再隨著井長的增加而增加。疏放水井的臨界長度c定義為疏放水井在一定直徑條件下,達到最大滲流量時的最小井長。由圖6也可以看出,井的半徑越大,滲流井的臨界長度c越小。不同半徑w條件下,疏放水井的臨界長度c的大小如表2所示。表2中=c/0,為疏放水井的臨界長度與含水層厚度比值。與w的關系如圖7所示,可以看出疏放水井的臨界長度隨井徑的增加呈對數函數減小關系,=–ln(w+)(2>0.99),其中、、為擬合參數。 圖6 滲流量與井長的關系 表2 不同半徑條件下疏放水井的臨界長度及其與含水層厚度比 圖7 k與Rw的關系 圖8 滲流量與井徑的關系 由圖8可以看出,不同井長疏放水井的滲流量隨著井徑的增加逐漸增加,且滿足=+w,a、b和c均為擬合參數,2=1且<1.0的函數關系。 由上述分析可知,在井下施工疏放水井時,并非與地面抽排水孔完全一樣,井長越長,滲流量或抽排水量越大。對于井下疏放水鉆孔,當長度過小時,如小于c,不能達到最大疏放水的效果;當長度過大時,如大于c,多余的鉆井尺寸沒有達到增加涌水量的目的,浪費施工時間、費用。而不同的井徑所對應的臨界長度不同,可以根據擬定鉆孔半徑確定最優鉆進尺寸,即鉆進的極限井長c,最優化鉆進方案。臨界長度c的界定對井下疏放水鉆進方案的確定具有重要指導意義。 由于當疏放水滲流井井長超過臨界長度c時,其滲流量與完整井滲流量一樣,為最大滲流量,可以采用式(1)進行滲流量計算。當疏放水井井長小于c時,其滲流量再采用Dupuit潛水完整井滲流公式計算將產生較大誤差。以半徑為1 m的井下疏放水滲流井為例,當井長小于c時,根據數值模擬結果,對不同井長條件下滲流井達到穩定滲流時所引起的水位降深進行統計(表3)。根據式(1)對滲流量s進行計算,并將其與數值模擬結果n進行對比,發現誤差很大,范圍在–16%~–33.4%。將+w代替水位降深,代入式(1)對其進行修正,如式(2)所示,采用修正后的Dupuit公式(2)對疏放水非完整井滲流量r進行計算,其結果與數值模擬結果n十分接近,與數值模擬結果相對誤差為–0.1%~ 2.8% (表3),相比以往方法該計算結果更為準確。 因此,在進行礦井涌水量預測時,應當考慮采動裂隙發育至含水層的高度及含水層的厚度和初始孔隙水壓,不能簡單的認為導水裂隙上部含水層的孔隙水壓力降低為0,采用“大井法”估算礦井涌水量。借助于修正的Dupuit公式計算,合理的將裂隙概化為等效孔徑疏放水孔,查明裂隙上部孔隙水壓力降低值及裂隙揭露含水層長度,可更準確預測礦井涌水量。 表3 潛水含水層滲流量計算(Rw=1.0 m) a.由含水層底部進行疏放水時,疏放水井上方會形成孔隙水壓力降低區,當疏放水井的井長較小時,在疏放水井中心上方孔隙水壓力大于0,且由下而上呈先增加后逐漸減小的規律分布。 b.當w c.將+w代替水位降深代入Dupuit潛水完整井計算公式對其修正,當w [1] Niskovskiy Y,Vasianovich A. Investigation of possibility to apply untraditional and ecologically good methods of coal mining under sea bed[C]//The Sixth International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers,1996,51–53. [2] SUN Yajun,XU Zhimin,DONG Qinghong,et al. Forecasting water disaster for a coal mine under the Xiaolangdi reservoir[J]. Journal of China University of Mining and Technology,2008,18(4):516–520. [3] ZHANG Jincai,SHEN Baohong. Coal mining under aquifers in China:A case study[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(4):629–639. [4] LI Tie,MEI Tingting,SUN Xuehui,et al. A study on a water-inrush incident at Laohutai coalmine[J]. International Journal of Rock Mechanics and Mining Sciences,2013,59:151–159. [5] 武雄,于青春,汪小剛,等. 地表水體下煤炭資源開采研究[J]. 巖石力學與工程學報,2006,25(5):1029–1036. WU Xiong,YU Qingchun,WANG Xiaogang,et al. Exploitation of coal resources under water body[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(5):1029–1036. [6] 武強,趙蘇啟,董書寧,等. 煤礦防治水手冊[M]. 北京:煤炭工業出版社,2013. [7] 方俊,張杰. 定向長鉆孔超前疏放頂板水技術在棗泉煤礦的應用[J]. 煤炭工程,2016,48(7):56–59. FANG Jun,ZHANG Jie. Application of advance roof dewatering with directional long borehole in Zaoquan mine[J]. Coal Engineering,2016,48(7):56–59. [8] HANG Yuan,ZHANG Gailing,YANG Guoyong. Numerical simulation of dewatering thick unconsolidated aquifers for safety of underground coal mining[J]. Mining Science and Technology(China),2009,19(3):312–316. [9] 尹尚先,張祥維,徐慧,等. “大井法” 中滲透系數及含水層厚度的優化[J]. 煤田地質與勘探,2015,43(5):53–56. YIN Shangxian,ZHAGN Xiangwei,XU Hui,et al. Optimization of permeability coefficient and aquifer thickness in large-well- method[J]. Coal Geology & Exploration,2015,43(5):53–56. [10] 陳沖,李文堯,徐世光. 大井法在煤礦涌水量預測中的應用[J]. 煤炭技術,2017,36(11):199–201. CHEN Chong,LI Wenrao,XU Shiguang. Application of large diameter method in estimation water inflow of coal mine[J]. Coal Technology,2017,36(11):199–201. [11] 李明山. 伯努利方程與井下探放水鉆孔涌水量計算[J]. 礦業安全與環保,1999,26(2):37–38. LI Mingshan. Bernouli Equation and calculation of water inflow rate from probing and discharging[J]. Mining Safety & Environmental Protection,1999,26(2):37–38. [12] 陳實,董書寧,李競生,等. 煤礦工作面頂板傾斜鉆孔疏放水井流計算方法[J]. 煤炭學報,2016,41(6):1517–1523.CHEN Shi,DONG Shuning,LI Jingsheng,et al. Analytical solution for slanted well in the roof of coal mine working face[J]. Journal of China Coal Society,2016,41(6):1517–1523. [13] 趙寶峰. 灰色關聯度在井下鉆孔疏放水效果分析中的應用[J]. 遼寧工程技術大學學報(自然科學版),2013,32(3):289–292. ZHAO Baofeng. Application of gray correlation in the effect analysis of underground drilling water drainage[J]. Journal of Liaoning Technical University(Natural Science Edition),2013,32(3):289–292. [14] 靳月燦,孫亞軍,徐智敏,等. 收縮開采期封閉不良鉆孔的涌水量預測研究[J]. 中國煤炭,2012,38(6):99–103. JIN Yuecan,SUN Yajun,XU Zhimin,et al. Research on water inflow prediction from bad sealed boreholes in contraction coal mining[J]. China Coal,2012,38(6):99–103. [15] 王文學,隋旺華. 某礦第四系底部含水層降水井群優化布置[J]. 煤田地質與勘探,2011,39(2):30–33.WANG Wenxue,SUI Wanghua. Optimization for dewatering well design in the Quaternary bottom aquifer[J].Coal Geology & Exploration,2011,39(2):30–33. The seepage characteristics of a single well dewatering from an unconfined aquifer bottom LI Yang1, WANG Wenxue2, XIAO Hang1, SUN Yi3, WANG Yun3, DI Mengna3 (1. Henan Province Bureau of Hydrology and Water Resources, Zhengzhou 450003, China; 2. Henan Province Key Laboratory of Rock and Soil Mechanics and Structural Engineering, North China University of Water Resources and Electric Power, Zhengzhou 450045, China; 3. Henan Province Geology and Mining Construction Engineering LTD, Zhengzhou 450007, China) Dewatering from an aquifer bottom for drain and depressurization is one common method to ensure safety mining. This method is significantly different from pumping from the ground. In order to study the seepage characteristics of the dewatering hole(well), the seepage characteristics of a single well dewatering from an unconfined aquifer bottom was taken as an example and studied using numerical simulation method. The results show that whenw aquifer; dewatering well; seepage flow; Dupuit formula National Natural Science Foundation of China(41602298);Henan Institution of Higher Education Key Scientific Research Project(16A410004) 李洋,1979年生,男,河南正陽人,碩士,高級工程師,從事水文地質、工程地質、地下水監測等領域的生產研究工作. E-mail:laymanlee13@ qq.com 王文學,1985年生,男,江蘇豐縣人,博士,講師,從事水文地質、工程地質等方面的教學科研工作. E-mail:wang603698305@163.com 李洋,王文學,肖航,等. 非承壓含水層底部單孔疏放水滲流特征[J]. 煤田地質與勘探,2019,47(3):154–159. LI Yang,WANG Wenxue,XIAO Hang,et al. The seepage characteristics of a single well dewatering from an unconfined aquifer bottom[J]. Coal Geology & Exploration,2019,47(3):154–159. 1001-1986(2019)03-0154-06 P641.4+1 A 10.3969/j.issn.1001-1986.2019.03.024 2018-10-06 國家自然科學基金項目(41602298);河南省高等學校重點科研項目(16A410004) (責任編輯 周建軍)1 假設條件及模型建立
1.1 假設條件
1.2 模型建立
2 模擬結果可靠性分析
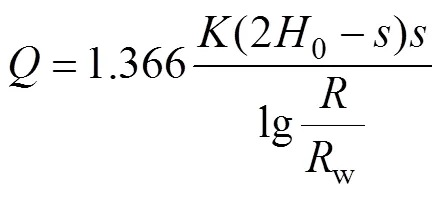
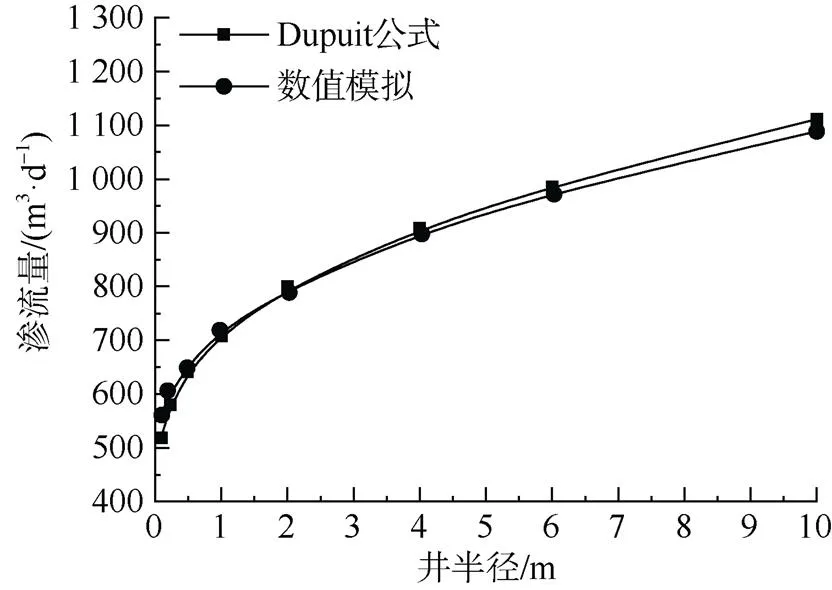
3 結果分析
3.1 疏放水井的滲流特征
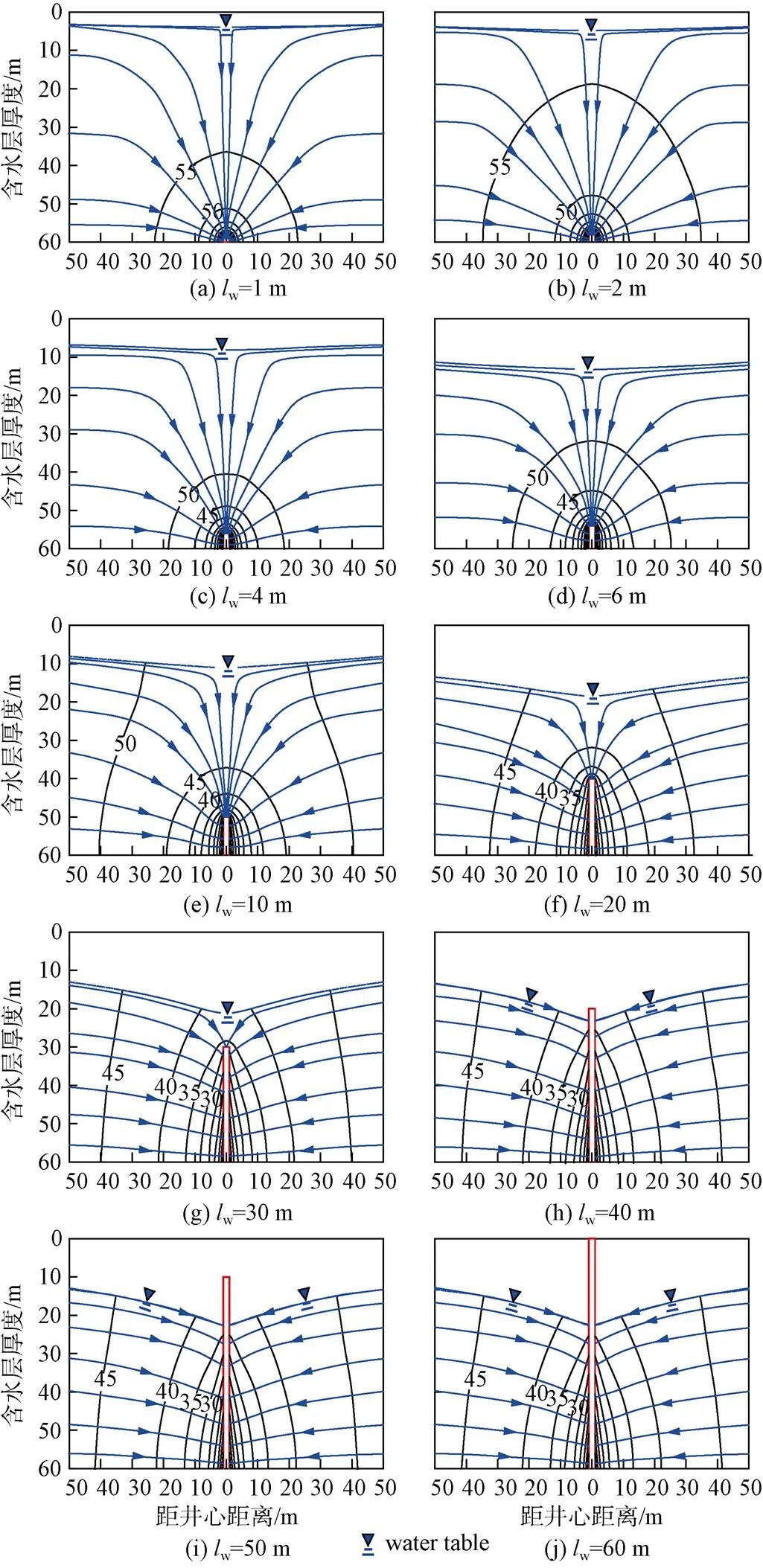
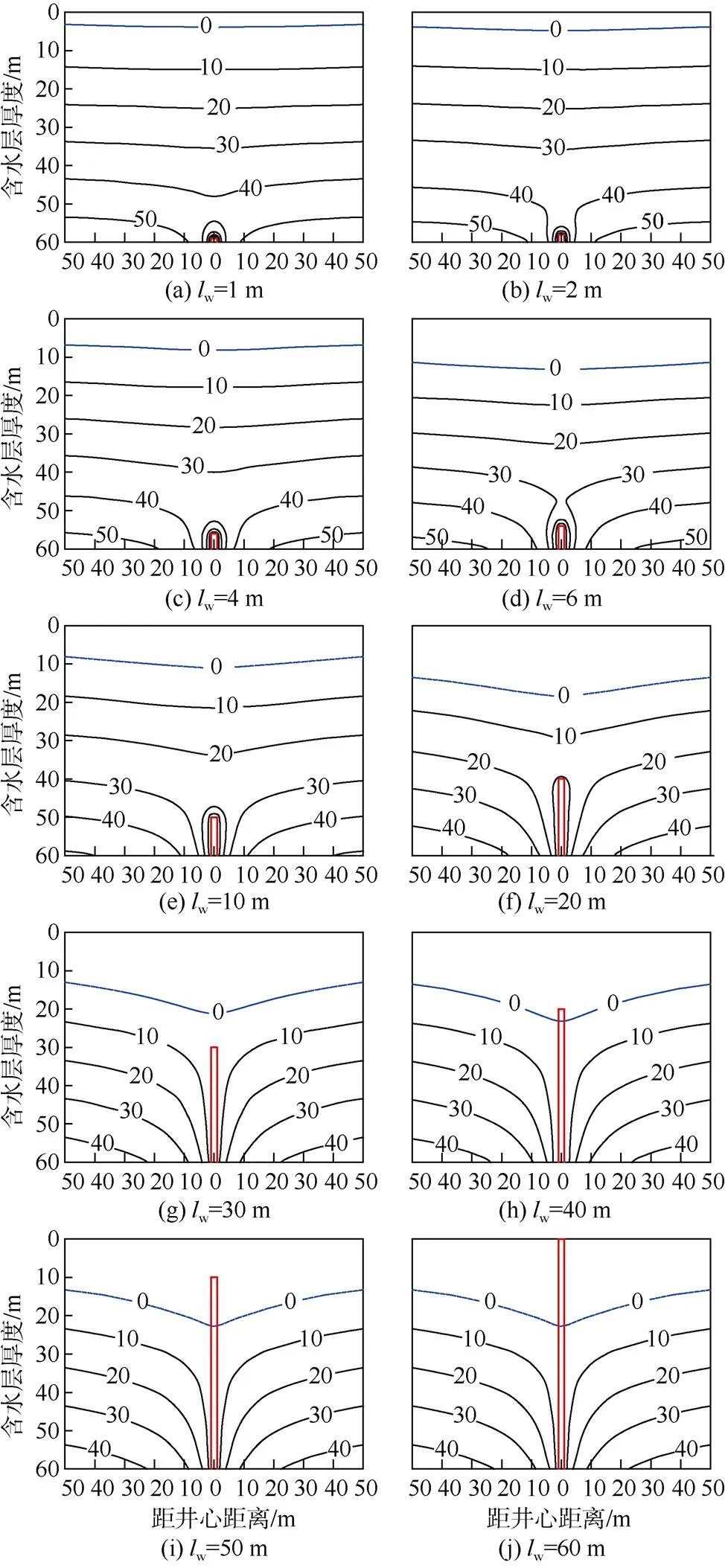
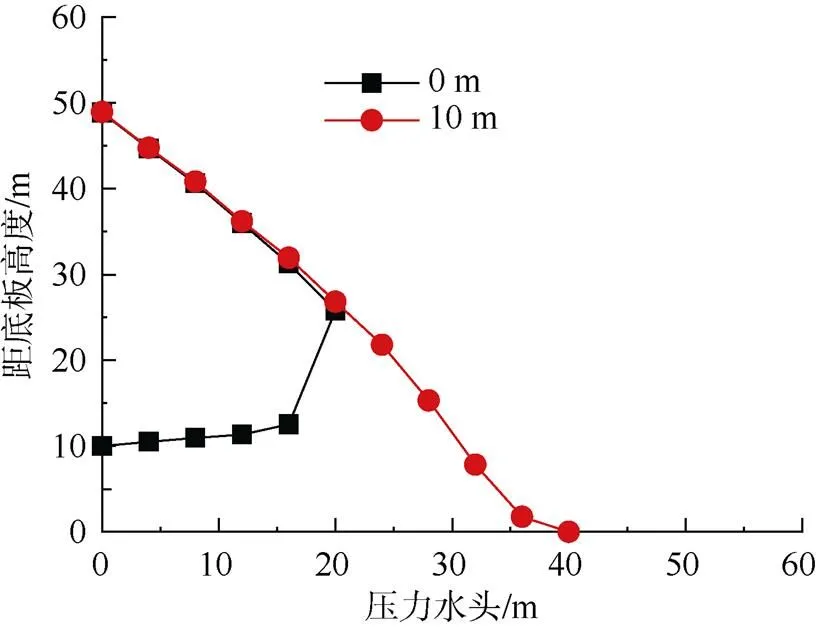
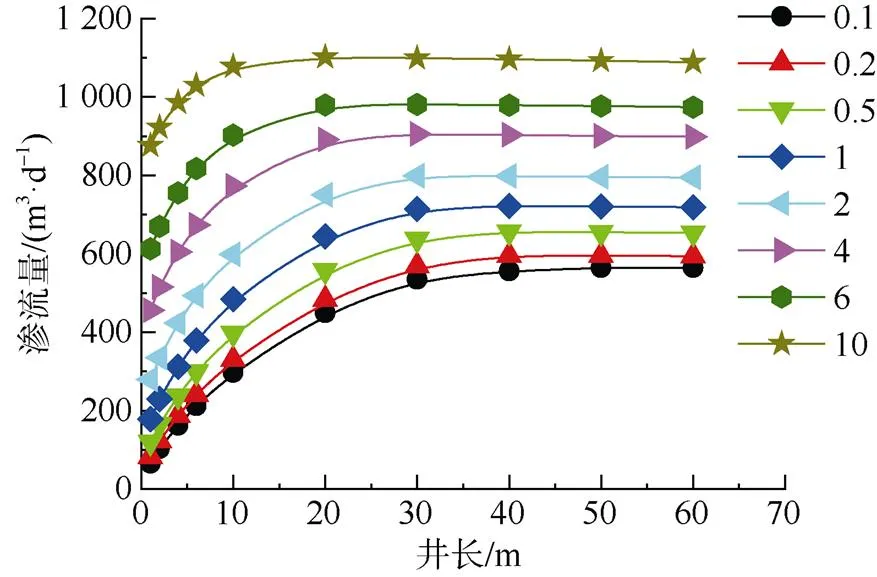
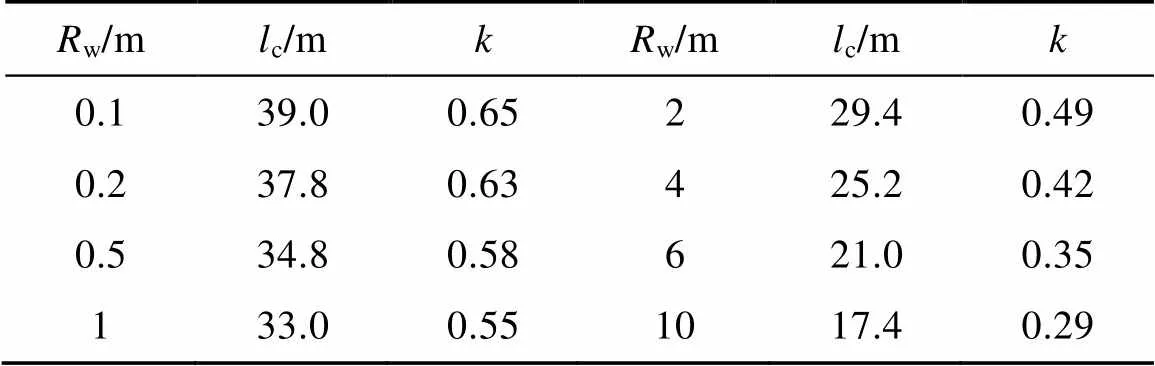
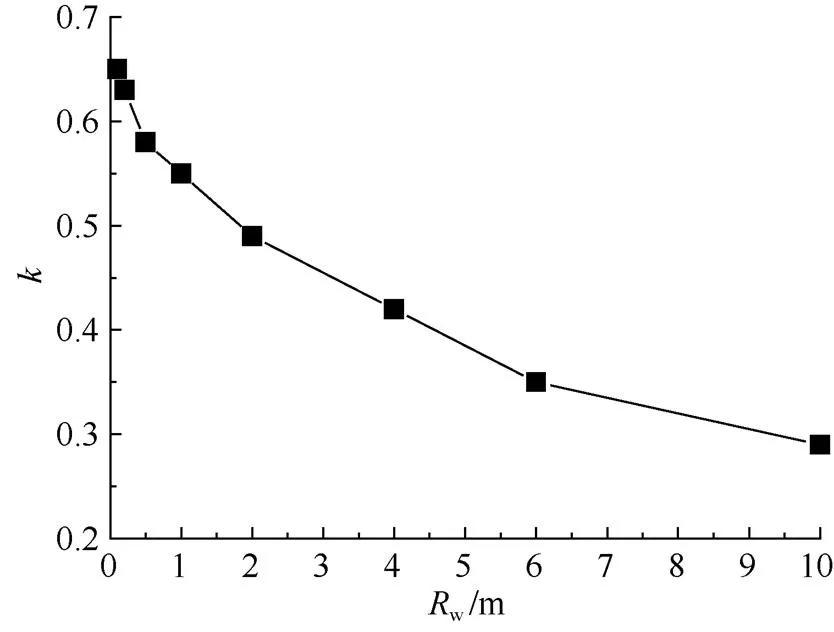
3.2 滲流量與井徑及井長關系
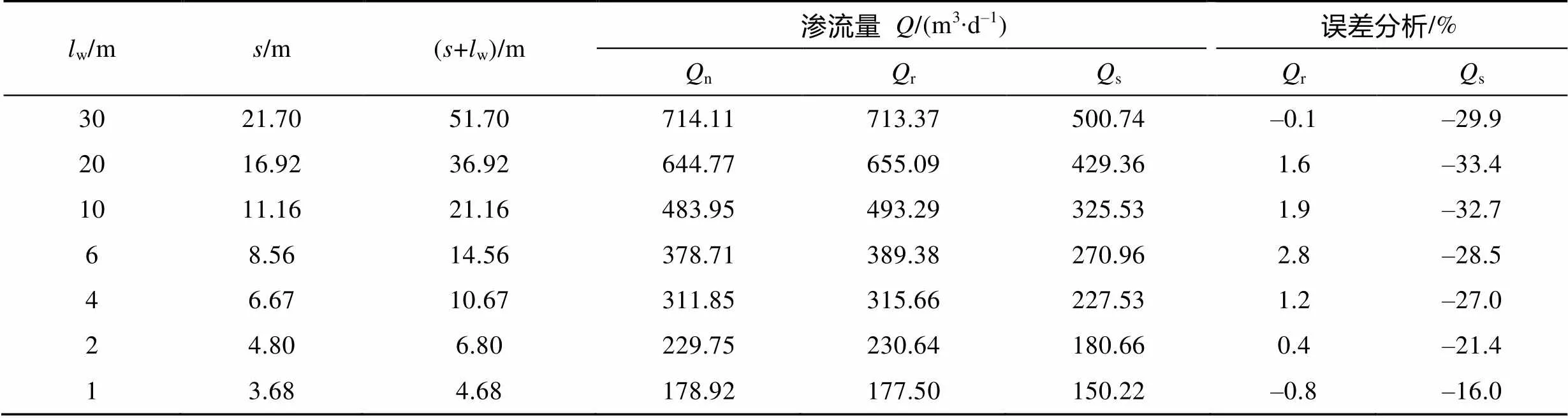
3.3 基于修正的Dupuit公式計算疏放水非完整井涌水量
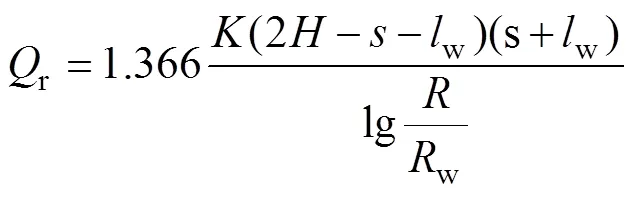
4 結論

