復雜環(huán)境對紅外空空導彈制導精度影響規(guī)律研究
李權成, 朱傳祥, 凡永華, 萬士正, 閆杰
(1.西北工業(yè)大學 航天學院, 陜西 西安 710072; 2.西北工業(yè)大學 機電學院, 陜西 西安 710072)
紅外空空導彈是最有效的近距空戰(zhàn)殺傷武器,并有數(shù)據(jù)顯示,半數(shù)的飛機在空戰(zhàn)中都是由紅外空空導彈擊落,這個比例正在不斷提高[1]。因此,研究針對紅外空空導彈的對抗策略,是十分有必要的。Timo等[2]建立了目標桶滾機動的簡易模型并利用伴隨法對其合理性進行了驗證,Imado等[3]在目標桶滾機動對導彈脫靶量影響方面進行了研究,但上述研究都未考慮誘餌影響。Arthur等[4]利用伴隨法[5]研究了目標機動和誘餌干擾對導彈脫靶量的影響,從而給出了相應的對抗策略,但其研究的是平面機動,且未考慮誘餌彈受力影響。黃鶴松等[6]基于真實數(shù)據(jù)建立了目標機動及面源誘餌的運動和輻射模型,并針對前向來襲導彈結合目標機動和誘餌投放進行了策略分析,但其對多誘餌的投放策略等研究較少。本文建立了紅外誘餌彈運動模型,并考慮誘餌彈壓制比差異,建立了紅外誘餌彈在干擾過程中的能量中心變化模型,然后研究了在空間中目標桶滾機動和誘餌投放對抗紅外導彈的戰(zhàn)術策略。
1 誘餌作用過程描述及建模
根據(jù)紅外誘餌彈的輻射特性可將其分為點源誘餌彈和面源誘餌彈[7]。本文針對點源誘餌進行建模仿真。
分析導彈對抗誘餌的過程,戰(zhàn)機投放誘餌彈至起燃時間[8],在導彈導引頭視場內(nèi)生成與目標紅外特性相近的輻射源,此時誘餌彈已脫離戰(zhàn)機一段距離,導引頭在一段時間內(nèi)無法分辨真實目標與誘餌,不失一般性,假設當導彈受到誘餌干擾時,視線指向目標與導彈的能量中心,即質(zhì)心干擾原理[9]。通常紅外誘餌彈投放技術參數(shù)有起燃時間、持續(xù)燃燒時間、齊投數(shù)量、組投放間隔、投射方向策略等。導彈抗干擾的過程可描述為4個階段[4,10],如圖1所示。
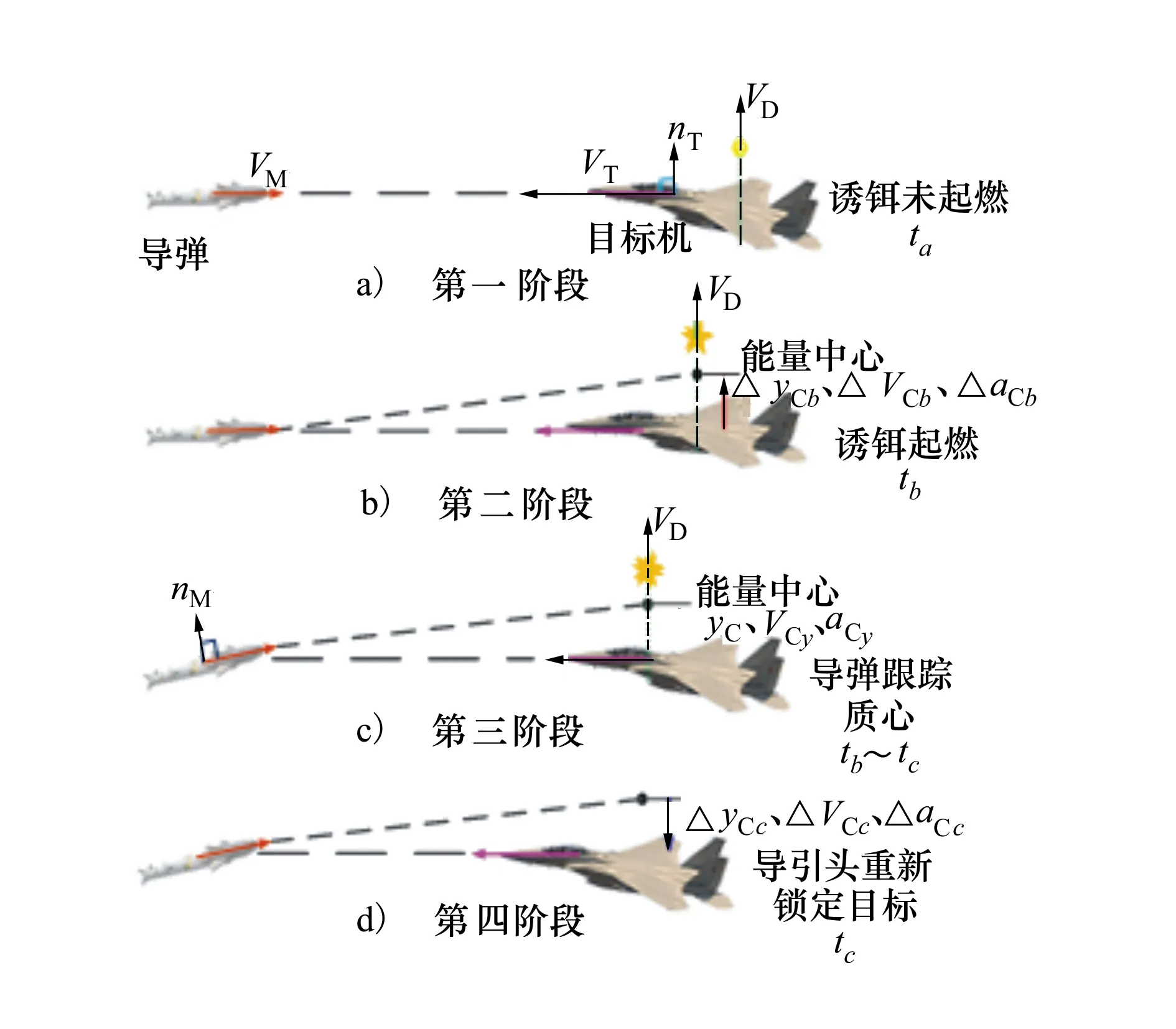
圖1 空空導彈與抗干擾過程
導彈末制導鎖定目標,此時載機導彈告警系統(tǒng)發(fā)出告警信號,在ta時刻發(fā)射誘餌,此時誘餌脫離戰(zhàn)機,但尚未起燃,如圖1a)所示。tb時刻誘餌彈燃燒后,由于導彈導引頭無法瞬時分辨誘餌和目標,導引頭將跟蹤誘餌和目標的能量中心,即“假目標”,能量中心位移、速度和加速度均會發(fā)生跳變,即目標視線角發(fā)生“突跳”,如圖1b)所示。且隨著誘餌和戰(zhàn)機的運動,“假目標”將按照一定的速度和加速度遠離戰(zhàn)機,且誘使導引頭鎖定“假目標”運動,如圖1c)所示。當經(jīng)過時間間隔tbc后,即在tc時刻導引頭通過抗干擾算法已成功分離誘餌和目標,導彈重新鎖定目標(假定目標未出導引頭視場,若此時目標已出視場,則導引頭丟失目標,不在本文討論之列),目標視線角發(fā)生“突跳”,如圖1d)所示。圖中VM,VT分別為導彈和目標的速度,Vc=VM+VT為彈目接近速度。為簡單起見,令初始目標視線角λ=0,彈目距離R=Vctgo,其中tgo=tF-t為剩余飛行時間,t為飛行時間,tF為遭遇點時刻,tF對應的彈目距離即為脫靶量。nM,nT分別為導彈和目標機動過載。VD為誘餌速度,yC,VCy,aCy為能量中心Y方向即鉛錘方向運動距離、運動速度以及加速度,并用Z方向代表水平方向。ΔyCb,ΔVCb,ΔaCb分別為誘餌彈起燃時能量中心位移、速度和加速度跳變值,ΔyCc,ΔVCc,ΔaCc分別為導彈重新鎖定目標后能量中心位移、速度和加速度跳變值。
為了有效地誘偏紅外制導空空導彈,紅外誘餌彈的輻射強度總是設計得比載機的紅外輻射強度大,動態(tài)時誘餌輻射能量與目標輻射能量比值即壓制系數(shù)K一般在2~3之間[11]。可認為目標一次齊投誘餌彈所形成的紅外輻射源強度為單個誘餌彈輻射強度之和[9],根據(jù)質(zhì)心干擾原理,假設目標機動和誘餌運動都在鉛垂平面進行,則Y方向能量中心可由(1)式求出,Z方向與Y方向類似。
(1)
式中,WD表示單個誘餌的輻射強度,WT表示目標的輻射強度,yD,VDy,aDy分別為誘餌彈Y方向的位移、速度和加速度,yT,VTy,aTy分別為戰(zhàn)機Y方向的位移、速度和加速度,n為誘餌彈一次齊投數(shù)目。
2 誘餌投放和目標機動對導彈干擾伴隨模型
2.1 紅外誘餌彈模型
誘餌彈在發(fā)射后主要受到重力和空氣阻力的作用。其運動方程如下
(2)
式中,f為誘餌彈所受阻力,Cd為阻力系數(shù),S為誘餌彈的迎風面積,ρ為大氣密度,mD為誘餌彈質(zhì)量,VDx,VDy,VDz為導彈速度在地面系的分速度,g為重力加速度。
誘餌彈初速度計算可參考文獻[12],本文討論桶滾機動中誘餌彈的初速度VDx0,VDy0,VDz0可通過(3)式進行計算
(3)
式中,VF為誘餌彈相對目標機發(fā)射速度,向桶滾機動外側投射時為正,反之為負。φ為投射誘餌時目標桶滾機動方位角。
以Y方向為例,建立誘餌彈模型,Z方向與此類似。為了方便建模,認為在導彈識別真實目標階段,誘餌彈加速度aDy為常值,其具體計算如下
(4)
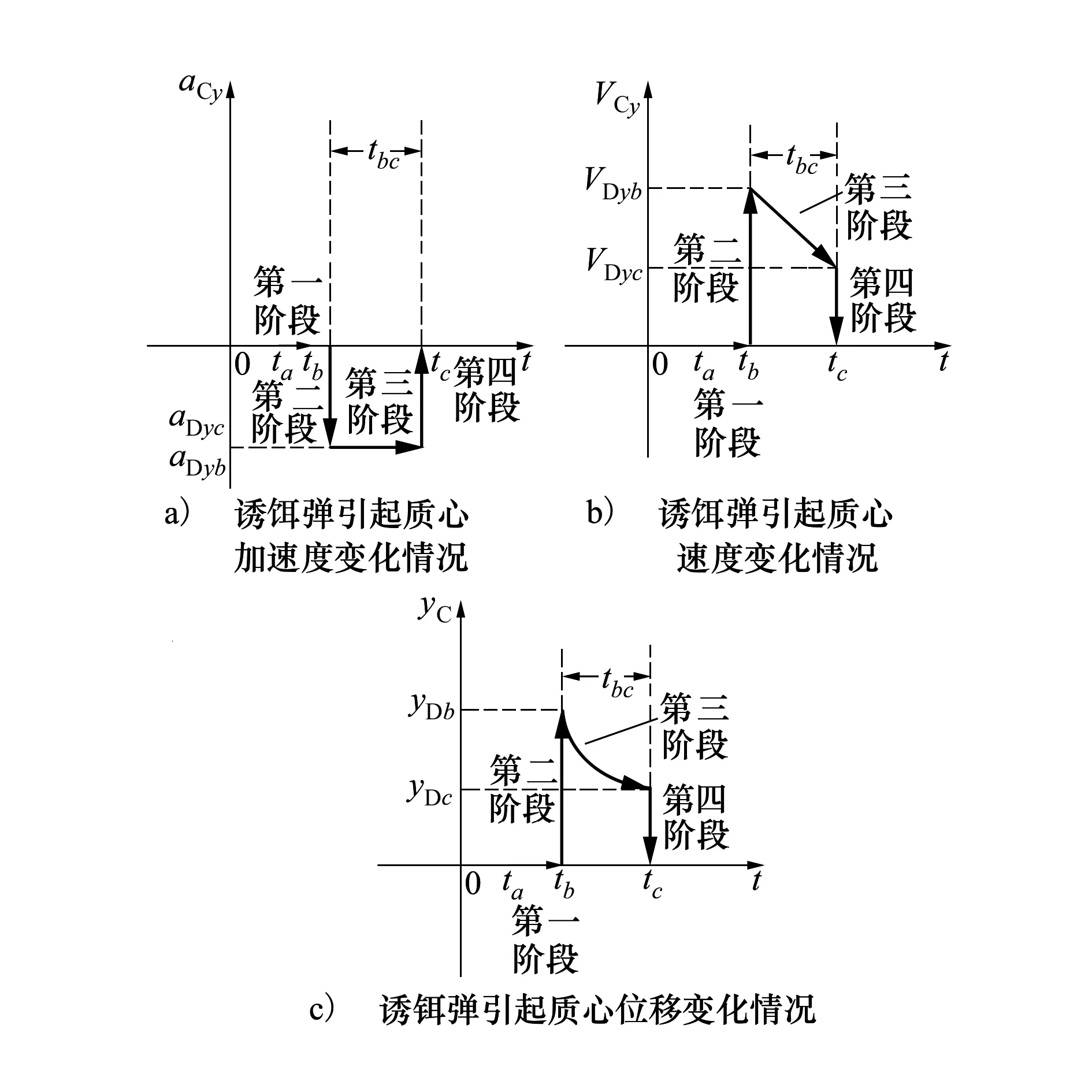
圖2 誘餌干擾過程
式中,VDyb為導彈跟蹤質(zhì)心起始tb時誘餌彈Y向速度,VDyc為導彈識別出目標時刻tc時誘餌彈Y向速度,tbc=tc-tb為誘餌彈誘偏作用時間,即導引頭抗干擾算法識別出真實目標時間。當目標無機動,根據(jù)上述討論可知,誘餌的干擾過程如圖2所示。圖2中誘餌在ta時刻發(fā)射,至tb時刻起燃,tc時刻被導引頭抗干擾算法剔除。yDb,yDc分別表示tb,tc時刻誘餌彈相對ta時刻的位移量,目標tb,tc時刻位移yTb,yTc定義與之類似。在第一階段(ta~tb),誘餌彈發(fā)射但尚未達到有效輻射強度,誘餌彈對導引頭視線角并未產(chǎn)生影響,則此階段誘餌彈引起的質(zhì)心加速度、速度和位移均未發(fā)生變化;在第二階段(tb),誘餌彈燃燒后,此時導引頭跟蹤對象不再是真實目標,而是誘餌與真實目標的能量中心/質(zhì)心,此時誘餌彈已經(jīng)脫離目標一段距離,質(zhì)心加速度、速度和位移均發(fā)生跳變,tb時刻由誘餌彈引起的質(zhì)心加速度跳變量ΔaDyb、速度跳變量ΔVDyb和位移跳變量ΔyDb可通過公式(5)計算;第三階段(tb~tc),由于之前已經(jīng)認為誘餌彈引起的質(zhì)心加速度為常值,則速度線性變化,位移呈拋物線型變化;第四階段,導引頭成功分辨誘餌與真實目標,其跟蹤對象從能量中心跳變回真實目標,tc時刻由誘餌彈引起的質(zhì)心加速度跳變量ΔaDyc、速度跳變量ΔVDyc和位移跳變量ΔyDc及tb時刻跳變量可表示為
(5)
誘餌干擾作用下能量中心的線性模型可以圖3所示采用脈沖函數(shù)的形式給出,圖中VCD表示由誘餌投放對質(zhì)心速度的影響量。
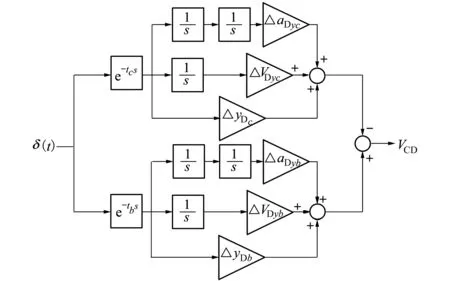
圖3 誘餌干擾作用下能量中心運動模型
2.2 目標機動模型
文獻[2]所述模型考慮到戰(zhàn)機桶滾機動時具備一定的法向初速度,但是通常的情況是戰(zhàn)機處于勻速巡航狀態(tài),即假定在導彈發(fā)射時目標處于勻速直線飛行狀態(tài),在導彈發(fā)射后目標先以額定過載能力做階躍形式的過渡機動,具備桶滾機動初速條件時,實施桶滾機動,該機動可以描述為戰(zhàn)斗機在桶滾橫截面做圓周運動,在X方向上作勻速直線運動。
假設桶滾機動起始相位角為φ0,目標額定過載能力為nT,桶滾機動角速度為ω,則目標桶滾機動初速VR=nTg/ω,階躍機動時間tstep=VR/(nTg)=1/ω,目標Y方向和Z方向的過載值為nTy,nTz,加速度值為aTy,aTz,則目標階躍機動時其值如(6)式所示。
(6)
則可以將目標機動形式轉化為脈沖輸入函數(shù),縱向加速度信號如圖4所示。

圖4 脈沖輸入的縱向加速度信號
分析圖3所示紅外空空導彈抗干擾過程,在不存在速度指向偏差和初始位移偏差情況下,桶滾機動對導彈脫靶量影響的模型如圖5所示:
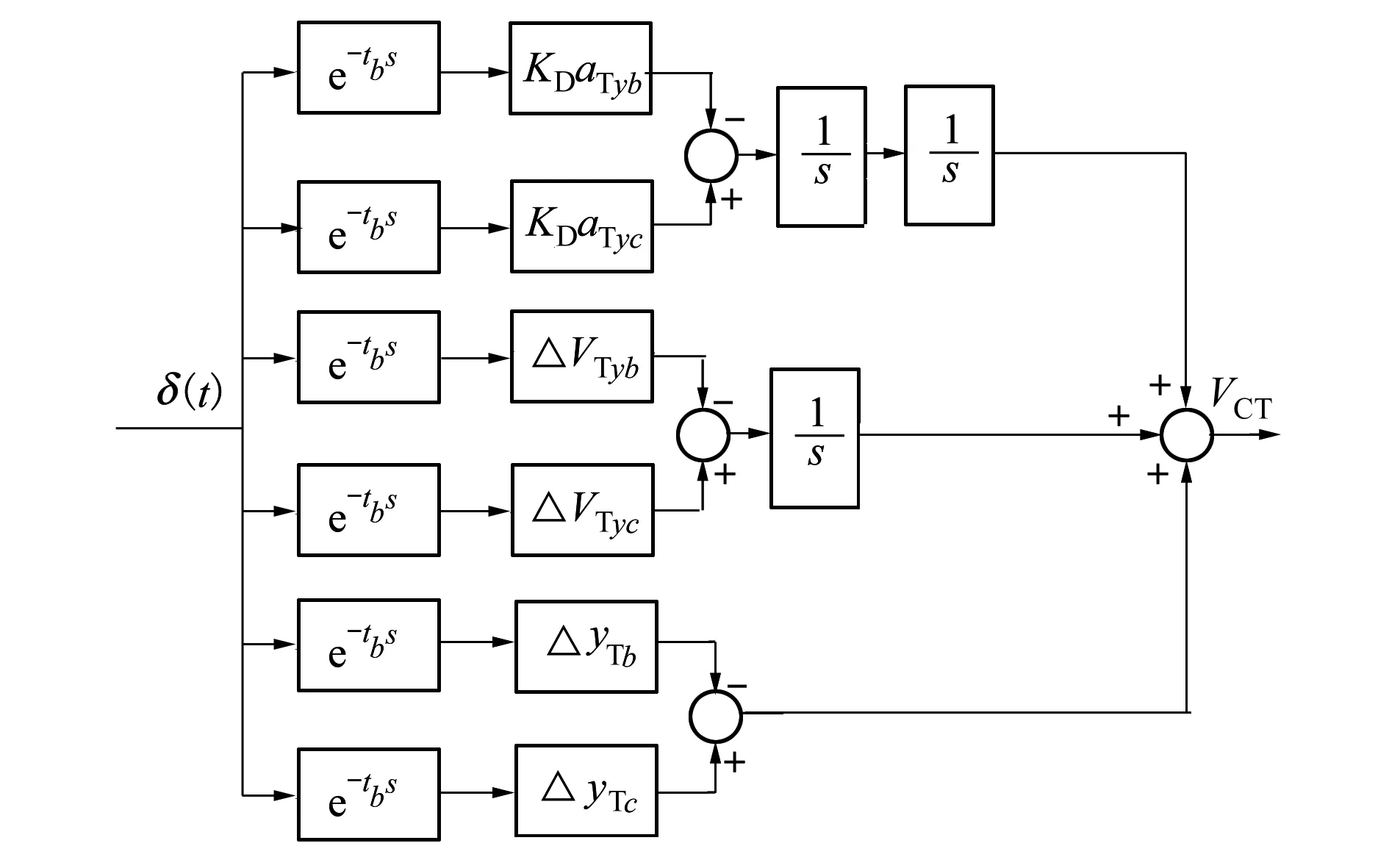
圖5 桶滾機動作用下能量中心運動模型
圖5中,VCT表示投射誘餌時由目標機動對質(zhì)心速度的影響量。根據(jù)公式(1)在誘餌開始工作即tb時刻,目標對質(zhì)心加速度的影響減小KD倍,在誘餌停止工作即tc時刻目標對質(zhì)心加速度的影響又增大KD倍。ΔVTyb,ΔyTb為tb時刻由于誘餌開始工作后目標使質(zhì)心產(chǎn)生的速度和位移跳變值,ΔVTyc,ΔyTc為tc時刻由于誘餌停止工作后目標使質(zhì)心產(chǎn)生的速度和位移跳變值。aTyb,aTyc分別為tb,tc時刻加速度跳變的輸入量,為了確保在加速度跳變時刻與aTy相位的一致性,需對正弦信號初始相位按照公式(7)進行調(diào)整,圖5所示為其轉化為脈沖輸入的形式。
(7)
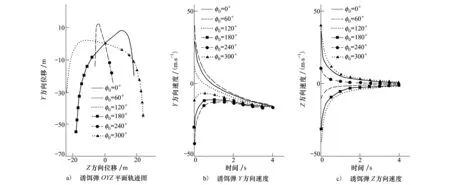
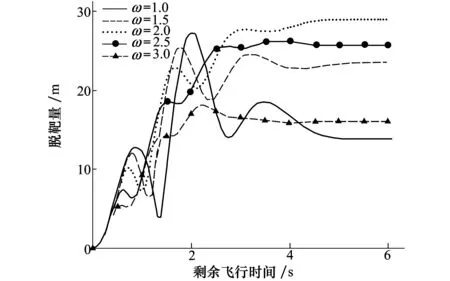
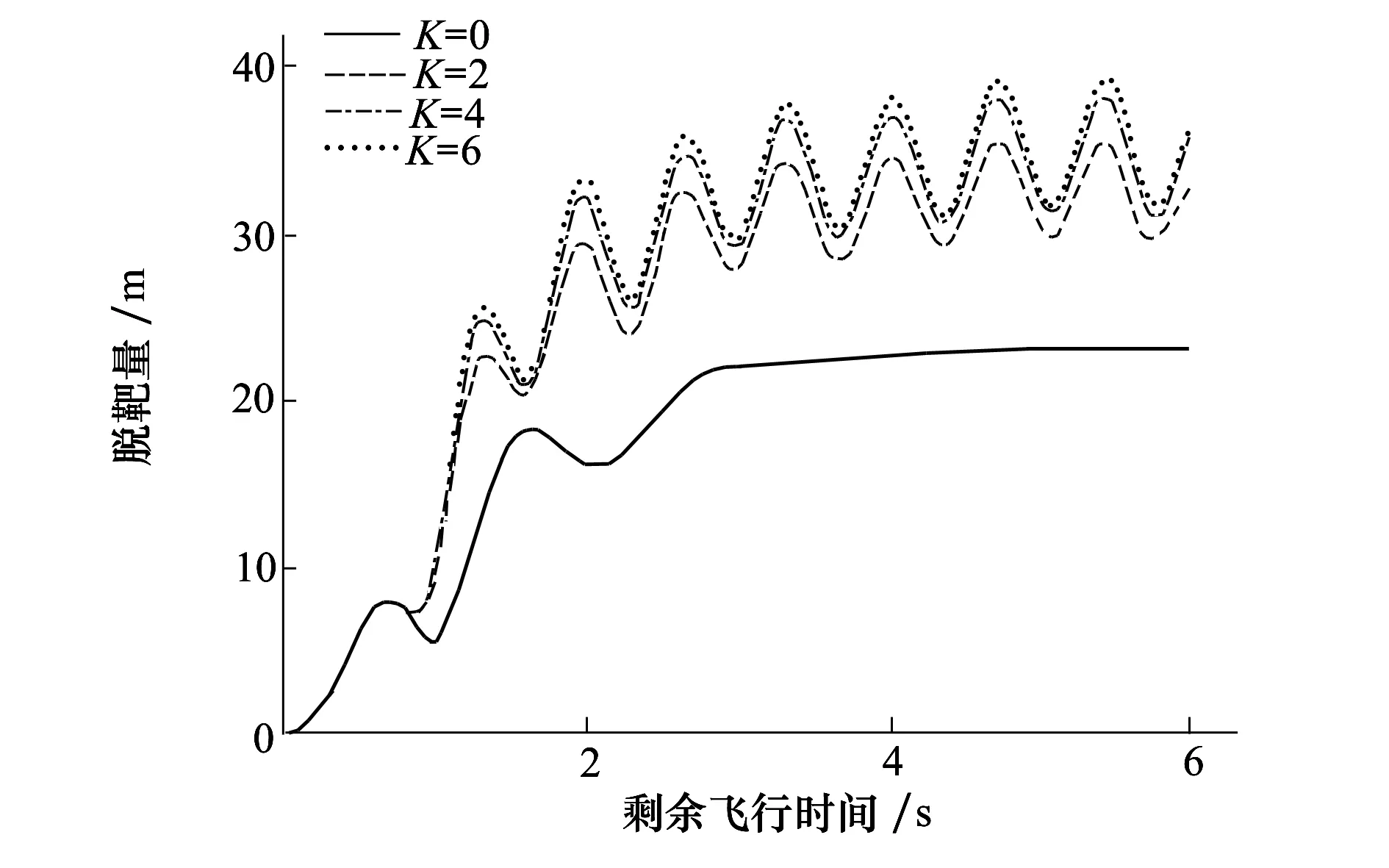
跳變量ΔVTyb,ΔyTb可由ta~tb時間段真實目標與質(zhì)心的初始位置差、初始速度差以及加速度差獲得,同理可計算ΔVTyc,ΔyTc,計算過程可由公式(8)表示,公式中t (8) 式中,VTya,VTyb分別表示ta和tb時刻目標的速度。在MATLAB仿真中通過積分、Enabled和Triggered等模塊可完成仿真模型的建立。運用該方法可以避免復雜的分情況討論以及參數(shù)推導,同時可以完成對更復雜機動方式和連續(xù)機動以及多誘餌投放的研究。 經(jīng)過上述討論,以Y方向為例,結合圖3所示VCD和圖5所示VCT計算模塊,建立一次誘餌投放過程中目標桶滾機動對導彈干擾線性化模型,如圖6所示。 圖6 導彈受目標機動和誘餌投放干擾線性化模型 圖6中模型參數(shù)[2]τSH表示導彈導引頭時間常數(shù),τN表示信號處理時間常數(shù),τAP表示導彈自動駕駛儀時間常數(shù),ωM表示導彈氣動響應角頻率,ζ表示導彈阻尼比,N為比例導引系數(shù),aMy為導彈y方向實際加速度值。 按照線性系統(tǒng)伴隨模型的建立準則[5,10],可建立目標桶滾機動和誘餌投放對導彈干擾伴隨分析模型。圖6所示模型有3個輸入,則導彈y方向脫靶量my可由伴隨模型3個輸出之和得到。同理可以建立z方向導彈脫靶量mz,則導彈總脫靶量mall計算公式為[13] (9) 對于多誘餌情況,只需在導彈伴隨分析模型外并聯(lián)相應時間的跳變量計算模塊即可,同時應用伴隨法,可通過一次伴隨仿真得到直接法需多次仿真才能計算的結果,計算效率顯著提高。 目標做桶滾機動過程中投放誘餌,某典型誘餌彈初始質(zhì)量為0.25 kg,質(zhì)量消耗率為0.03 kg/s,迎風面積S為0.003 2 m2,燃燒時間為4 s,發(fā)射速度VF為30 m/s,發(fā)射角為90°,取起燃時間為0 s,Cd=0.3,發(fā)射時戰(zhàn)機飛行高度為3 km,過載為6g,速度為0.8Ma,桶滾角速率為2 rad/s,則可求得誘餌彈在地面系的速度,誘餌彈在地面系位移量可通過對速度積分求得,在目標機桶滾相位角分別為0°,60°,120°,180°,240°,300°時投射誘餌彈,其OYZ平面軌跡圖及速度隨時間變化情況如圖7所示。 圖7 誘餌投放軌跡及速度變化曲線 誘餌彈投放組間隔應不小于tbc,因為如果在前一組誘餌尚未移出導彈視場或目標尚未被導彈識別之前投放下一組誘餌,會影響前一組誘餌形成的質(zhì)心干擾,使質(zhì)心向目標方向移動[4]。實際作戰(zhàn)中,作戰(zhàn)態(tài)勢、誘餌彈的齊投數(shù)量、方向、速度等都會造成導引頭識別真實目標時間的差異,為進行規(guī)律分析此處認為導引頭識別真實目標時間不發(fā)生變化,本文取tbc=0.5 s。通過計算可得不同桶滾機動起始相位角時誘餌彈各時刻位移、速度和加速度值。 仿真條件:取最大剩余飛行時間tmax=6 s,τSH=0.1 s,τN=0.11 s,τAP=0.15 s,ωM=18 rad/s,ζ=0.7,N=4,Vc=1 500 m/s,φ0=0°,ω選為1 rad/s,1.5 rad/s,2 rad/s,3 rad/s,4 rad/s,導彈尾后追擊目標機,其余仿真參數(shù)設置同圖7,研究桶滾機動角速率對導彈脫靶量影響。導彈脫靶量隨剩余飛行時間變化情況如圖8所示。 從圖8中可以看出,該仿真條件下,當剩余飛行時間大于2.5 s,桶滾角速率在2~3 rad/s時產(chǎn)生的脫靶量最大,均大于25 m,所以要使導彈產(chǎn)生足夠大的脫靶量,戰(zhàn)機必須具備充裕的時間進行桶滾機動,戰(zhàn)機應盡量將導彈置于尾后以消耗導彈能量并增加剩余飛行時間。 圖8 各桶滾角速率值對應脫靶量隨tgo變化曲線 3.3.1 誘餌彈齊投數(shù)量、投放組間隔對導彈脫靶量影響 紅外誘餌彈參數(shù)設置同圖7,相對目標機身垂直向下投射,投放組間隔為0.7 s,目標桶滾機動角速率為2 rad/s,其余參數(shù)與圖8相同。投射1枚誘餌的壓制比K=2,則齊投n枚時K=2n,齊投數(shù)量對導彈脫靶量影響如圖9所示,圖中K=0表示目標只做桶滾機動不投放誘餌。 圖9 不同K時導彈脫靶量隨tgo變化曲線 (10) 式中,m(tgo)表示伴隨模型所得tgo對應的導彈脫靶量。誘餌彈投放組間隔從0.5~4.1 s間隔0.2 s變化,則得導彈平均脫靶量隨投放組間隔變化如圖10所示。 圖10 不同K時導彈平均脫靶量隨投放組間隔變化曲線 從圖9可以看出,在該投放組間隔下,導彈脫靶量存在多個極值和極小值,投誘餌比不投誘餌能產(chǎn)生更大的脫靶量,齊投數(shù)量越多,脫靶量越大。同時,從圖10可得齊投數(shù)量越多,投放組間隔越小,導彈平均脫靶量越大,投誘餌比不投誘餌能產(chǎn)生更大的平均脫靶量,但是隨著齊投數(shù)量的增大,平均脫靶量增長幅度越來越小,因為戰(zhàn)斗機攜帶誘餌彈數(shù)量有限,并且一般要對抗多次導彈來襲,則在該仿真條件下,誘餌彈齊投數(shù)量在2或3,投放間隔小于1 s為宜。 3.3.2 起燃時間、投放策略對導彈脫靶量影響 誘餌投放策略選為“向外”、“向內(nèi)”、“外內(nèi)外”和“內(nèi)外內(nèi)”4種,其具體投放方式如圖11所示。 圖11 4種誘餌彈投放策略 圖11中圓表示桶滾機動橫截面,“內(nèi)”和“外”指誘餌投射是朝圓周運動的內(nèi)側或外側投射,假設桶滾一周投射8組誘餌,投射速度依次為VD1~VD8,其大小相同但方向不同。選取仿真條件如下:桶滾機動起始相位角為0°,齊投數(shù)量為2,投放組間隔為0.7 s,起燃時間從0~0.6 s間隔0.1 s變化,其余仿真條件不變,則導彈平均脫靶量變化如圖12所示。 圖12 不同投放策略下導彈平均脫靶量隨起燃時間變化曲線 從圖12可以得出,在相同起燃時間情況下,采用向外投放策略,會使導彈平均脫靶量達到最大,向內(nèi)投放策略平均脫靶量最小,其余2種投放策略介于兩者之間。所有投放策略的平均脫靶量隨起燃時間的增加而增大,但導彈導引頭視場角很小,起燃時間過長會使誘餌彈起燃時距離目標過遠甚至已出視場從而起不到干擾作用。所以,桶滾機動中應選取向外投射誘餌策略,同時起燃時間應適中。 文中建立了更為實際的目標桶滾機動模型、誘餌投放模型和對導彈制導精度的伴隨分析模型,研究了目標桶滾機動和紅外誘餌彈對紅外制導導彈脫靶量影響。在導彈告警系統(tǒng)發(fā)出告警信號后,目標機應將導彈置于尾后,階躍機動達到速度條件后進行角速率為2~3 rad/s的桶滾機動,同時向桶滾機動橫截面外側即相對戰(zhàn)機向下投放誘餌彈。典型條件下誘餌彈投放時組間率隔盡可能接近導引頭識別時間,每組投放2或3枚誘餌,同時合理控制誘餌彈起燃時間。本研究對于目標機動逃逸及誘餌彈投放具有指導意義。2.3 伴隨分析模型的建立
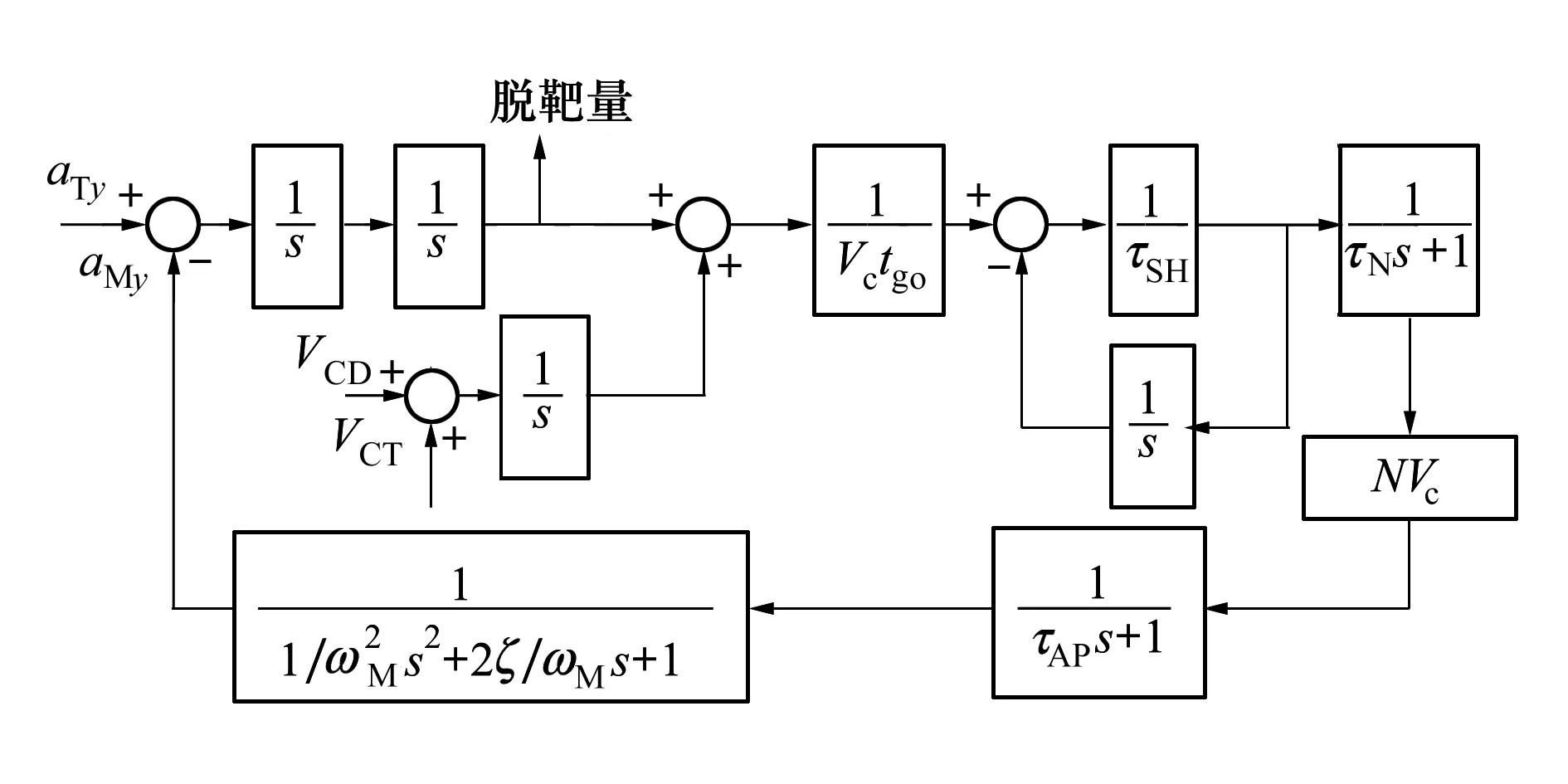
3 仿真與分析
3.1 目標桶滾機動與誘餌投放仿真結果
3.2 桶滾機動對導彈脫靶量影響分析
3.3 桶滾機動時誘餌投放對導彈脫靶量影響分析

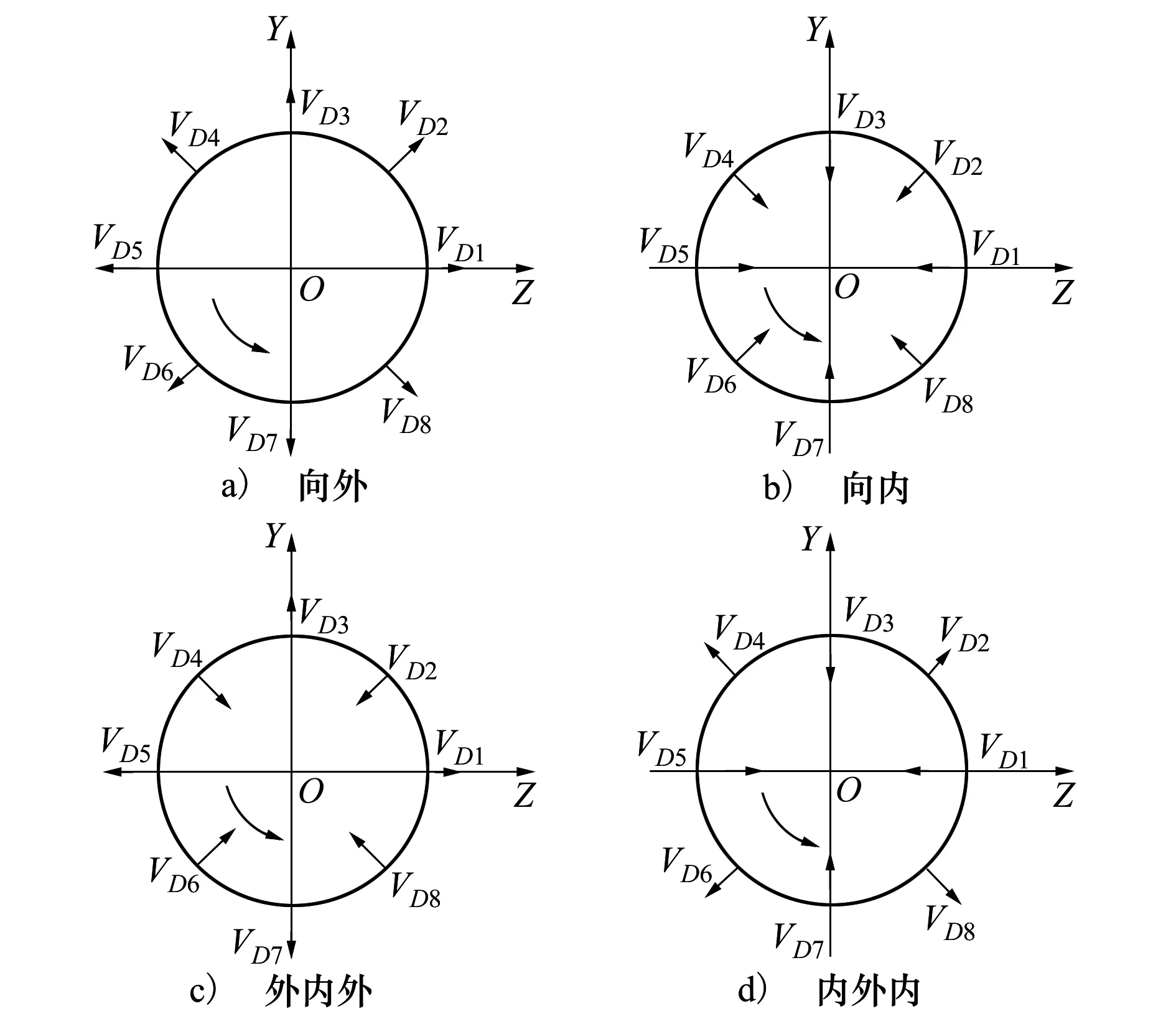
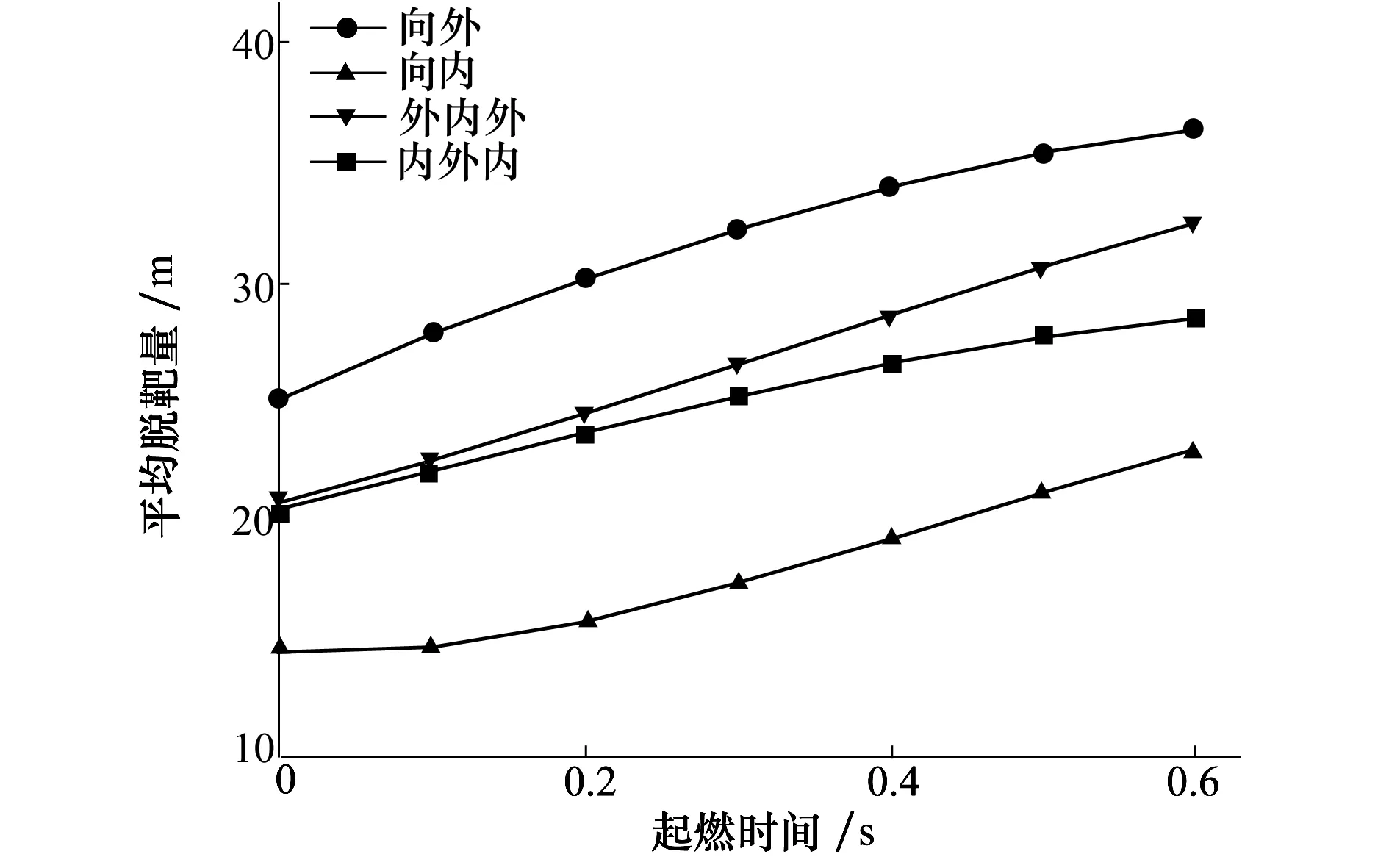
4 結 論

