變厚度胞體壁多孔夾層材料的主動散熱性能研究

董浩, 都琳, 張凱, 崔迪, 鄧子辰

(1.西北工業大學 理學院, 陜西 西安 710072; 2.西北工業大學 力學與土木建筑學院, 陜西 西安 710072； 3.中國人民解放軍 61267部隊, 北京 101114; 4.復雜系統動力學與控制工信部重點實驗室, 陜西 西安 710072)

多孔夾層材料是構成胞體的邊界和表面的支柱或平板相互連通成網絡結構的材料[1]。隨著現代工業裝備技術的發展，多孔夾層材料以其優良的結構效率和隔熱降噪等性能備受科研人員和工業技術人員的青睞，被廣泛應用于現代建筑、軍事裝備和交通運輸等諸多領域[2-4]。

近年來，多孔夾層材料作為一種超輕結構材料，其主動散熱性能成為學術界關注的熱點。Lemos等[5]研究了橢圓柱多孔夾層材料的傳熱系數及散熱性能，并發現在相同的質量流率下，橢圓柱構型比方形構型具有更低的傳熱系數。Zhang等[6]采用了有限元與有限差分混合的快速數值方法，研究了在強迫對流條件下梯度金屬多孔夾層材料的散熱性能，并獲得了固體壁面和流體沿著流動方向的溫度分布。Ferkl等[7]分析了一維多孔夾層材料模型中的熱傳遞，并給出了其等效熱導率，為研究三維多孔夾層材料的熱傳遞打下了基礎。Mukherjee等[8]建立了具有多孔夾層結構的超燃沖壓發動機的一維傳熱模型，并研究了其燃燒器表面的主動散熱性能。Eusebio等[9]討論了對流、輻射、傳導邊界條件下，胞體結構的性質對聚合泡沫金屬和多孔金屬材料的散熱性能影響，并指出在高熱通量情況下，相對密度對多孔材料散熱性能的影響是最大的。楊微[10]基于FE-FDM方法對四邊形蜂窩結構散熱器的結構尺寸和拓撲構型進行優化設計，使蜂窩結構整體散熱性能提高了50%左右。張凱等[11]考慮了對流換熱的邊界條件下多孔夾層材料的主動散熱性能，發現正六邊形構型的多孔夾層材料具有顯著的主動散熱性能優勢。雷鴻等[12]利用場協同原理分析了泡沫材料的對流換熱機制，并指出在使用泡沫材料作為散熱器的核心部件時，應選擇空隙大小較為均勻的材料。王浩[13]基于蒙特卡洛和熱網絡法建立了導熱和輻射換熱耦合條件下金屬蜂窩結構的傳熱計算模型，指出減小蜂窩結構的孔隙率可以提高金屬蜂窩結構熱防護性能。吳一昊等[14]建立了考慮輻射效應金屬蜂窩芯板的有限元傳熱模型，發現輻射換熱是蜂窩結構的主要傳熱方式。

從以上研究成果可以發現，無論是理論計算還是實驗分析，都是在等厚度胞體壁的條件下進行的，而自然和工程實例告訴我們，變厚度胞體壁多孔夾層材料具有更優的性能。因此，本文將通過推導變厚度胞體壁多孔夾層材料的散熱系數，分析胞體壁厚度變化下，不同胞體構型多孔夾層材料的相對密度與散熱系數的關系，進而研究胞體壁厚度變化對各種胞體構型多孔夾層材料的主動散熱性能的影響。本文的研究可為變厚度胞體壁多孔夾層材料的結構優化提供一定的理論基礎。

1 研究模型及其相關參數

1.1 研究模型

本文分析的散熱器模型和多孔夾層材料胞體構型如圖1和圖2所示，其中胞體的構型分為三連通正方形、四連通正方形、四連通三角形、六連通三角形和六邊形。上下壁面保持恒定溫度Tw。速度為V0,溫度為T0,壓強為p0的冷卻流體在入口處進入多孔夾層結構。在出口處,流體的溫度為Te,壓強為pe。Ωf,vf,μf,cp分別表示恒定壓降下的流體密度、運動黏度、剪切黏度和比熱容。

圖1 分析模型

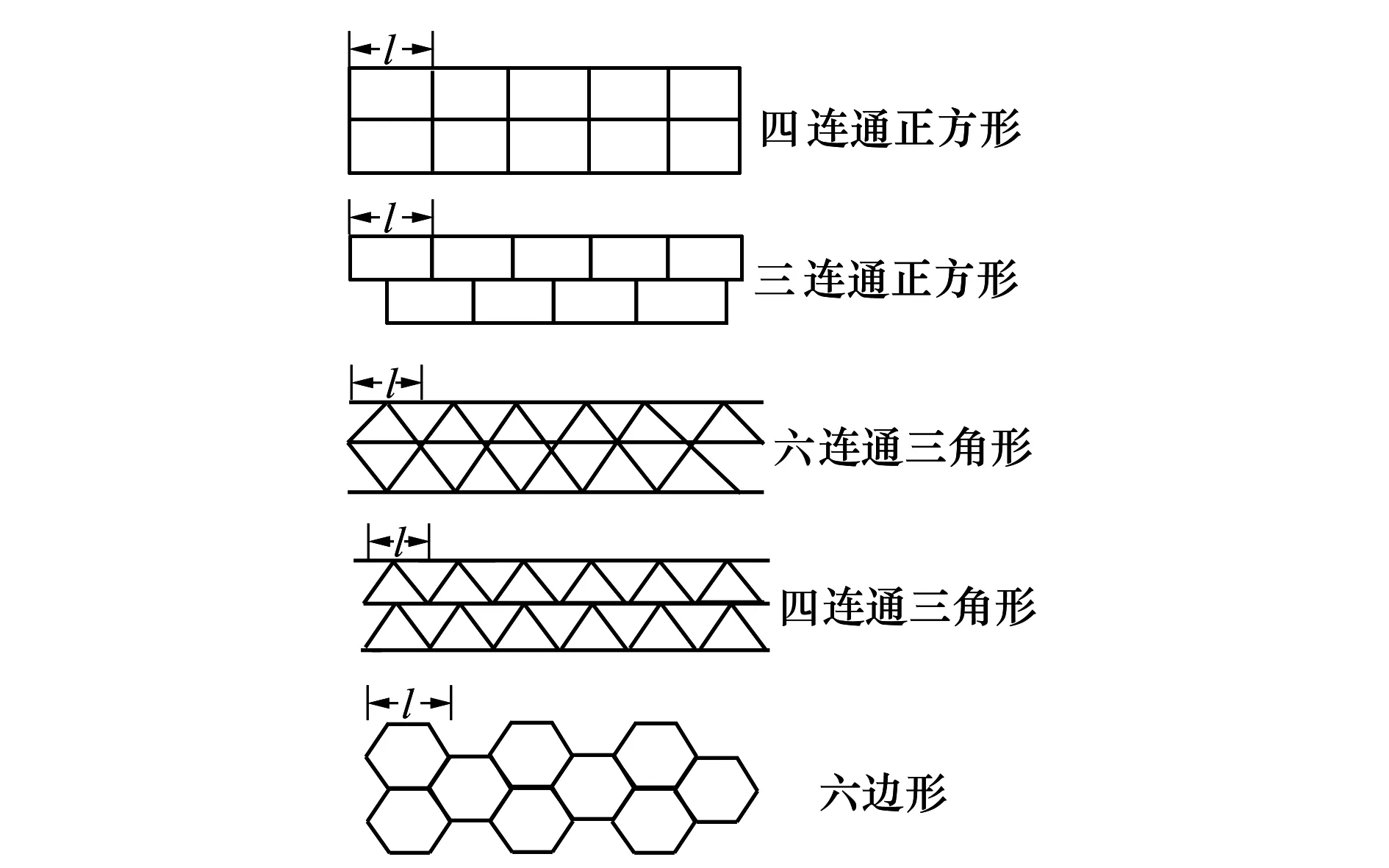
圖2 胞體結構形式

1.2 相對密度

變厚度胞體壁多孔夾層材料模型如圖3所示。

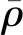
三角形、正方形和六邊形胞體構型多孔夾層材料的長寬比t/l為

(4)

(5)

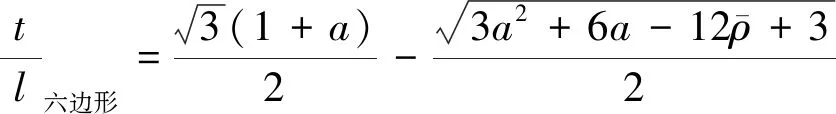
(6)

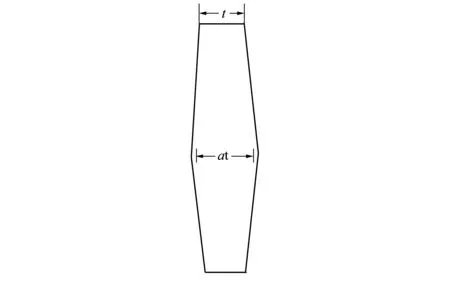
圖3 變厚度胞體壁

1.3 壓降

每種胞體構型的表面積密度αa為

(7)

其中表面積密度系數為ca,每種胞體構型的水力直徑Dh為

(8)

由Hagen-Poiseuille動量方程可以得到多孔夾層材料的壓降Δp

(9)

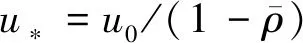
2 多孔夾層材料散熱系數的建立

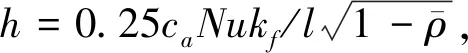
(10)

式中努塞爾特數為Nu,流體熱導率為kf,沿著胞體長度的局部坐標為ξ。考慮等溫的邊界條件T(0,x)=T(cHH,x)=Tw,其中cH為胞體壁彎曲系數,解此方程得

(11)

從上下壁面流入空氣的熱量為

qw(x)=2h(W-Nscwt)[Tw-Tf(x)]

(12)

式中，Ns=cnW/l從上下壁面流入流體中的熱量為

(13)

由流經結構氣體的能量守恒可以得到

cp「Tf(x+dx)-Tf(x)?=nNsq+qw

(14)

解得

Tf(x)=Tw-(Tw-T0)exp(-x/L*)

(15)

式中

(16)

則氣體的平均溫度為

(17)

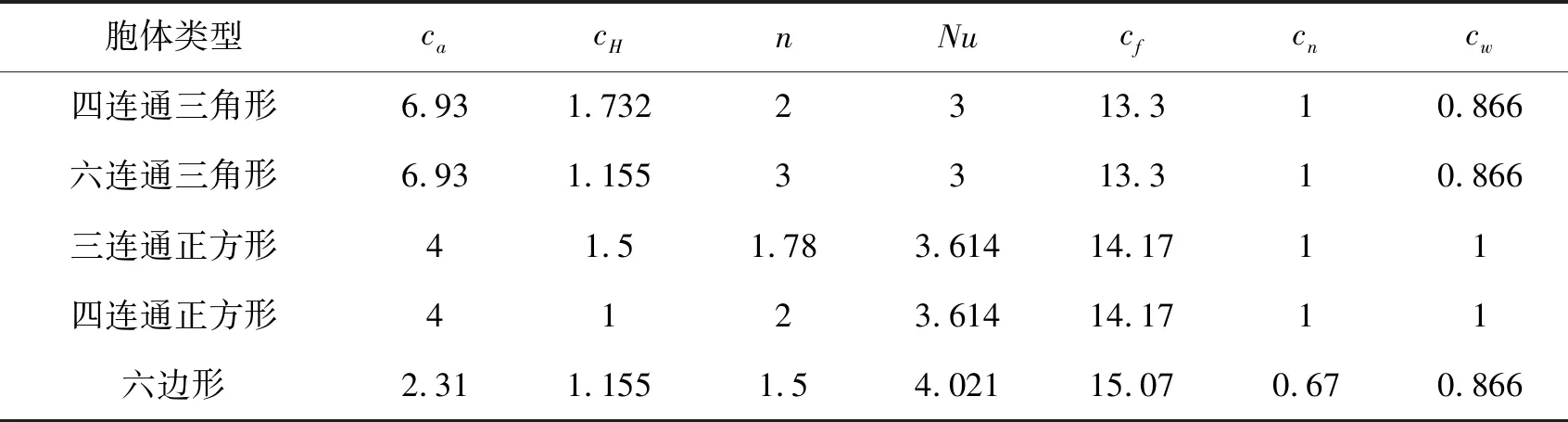
表1 多孔夾層材料中各種胞體構型的相關參數

由多孔夾層材料中氣體的溫度分布,可以得到氣體流經多孔夾層材料后消散的總熱量為

Q=mcp(Te-T0)=mcp(Tf(L)-T0)

(18)

多孔夾層材料的總傳熱系數為

(19)

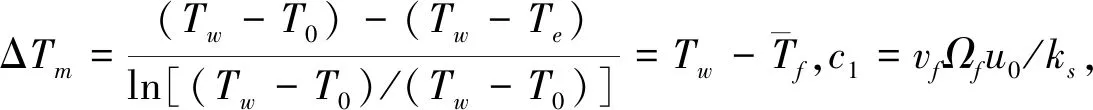
(20)

3 胞體壁厚度變化對多孔夾層材料主動散熱性能的影響與分析

其中l=1 mm,L/l=100,H/l=10,ks=

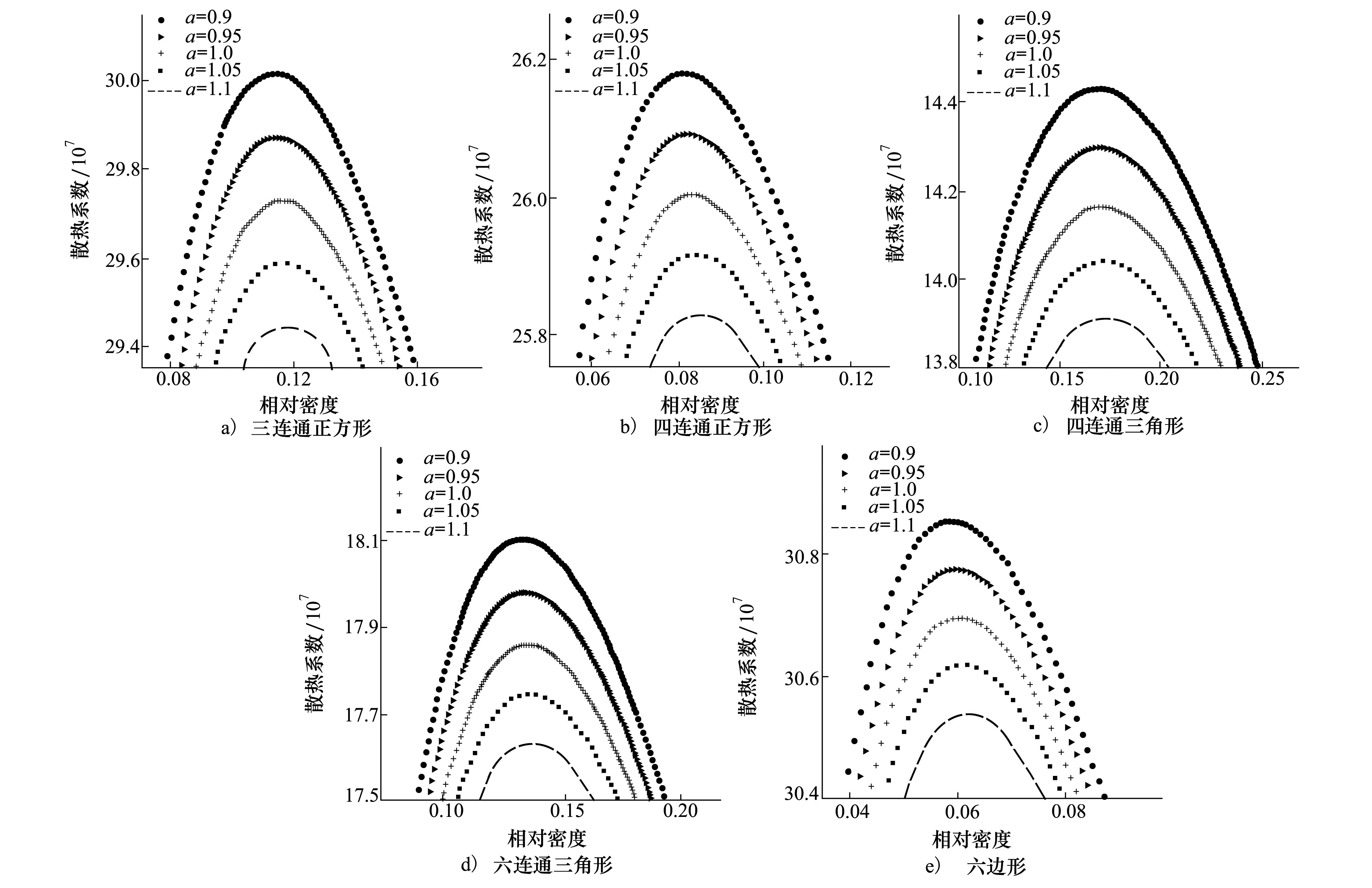
圖4 不同胞體構型多孔夾層材料的相對密度與散熱系數的關系

隨著厚度參數a的增大,六連通三角形的最佳相對密度增大最快,而六邊形增大最慢,三連通正方形的最大散熱系數下降最快,而六邊形的最大散熱系數下降最慢。這表明厚度的變化對六邊形單元的主動散熱能力影響小,而對三角形和正方形單元的影響大。

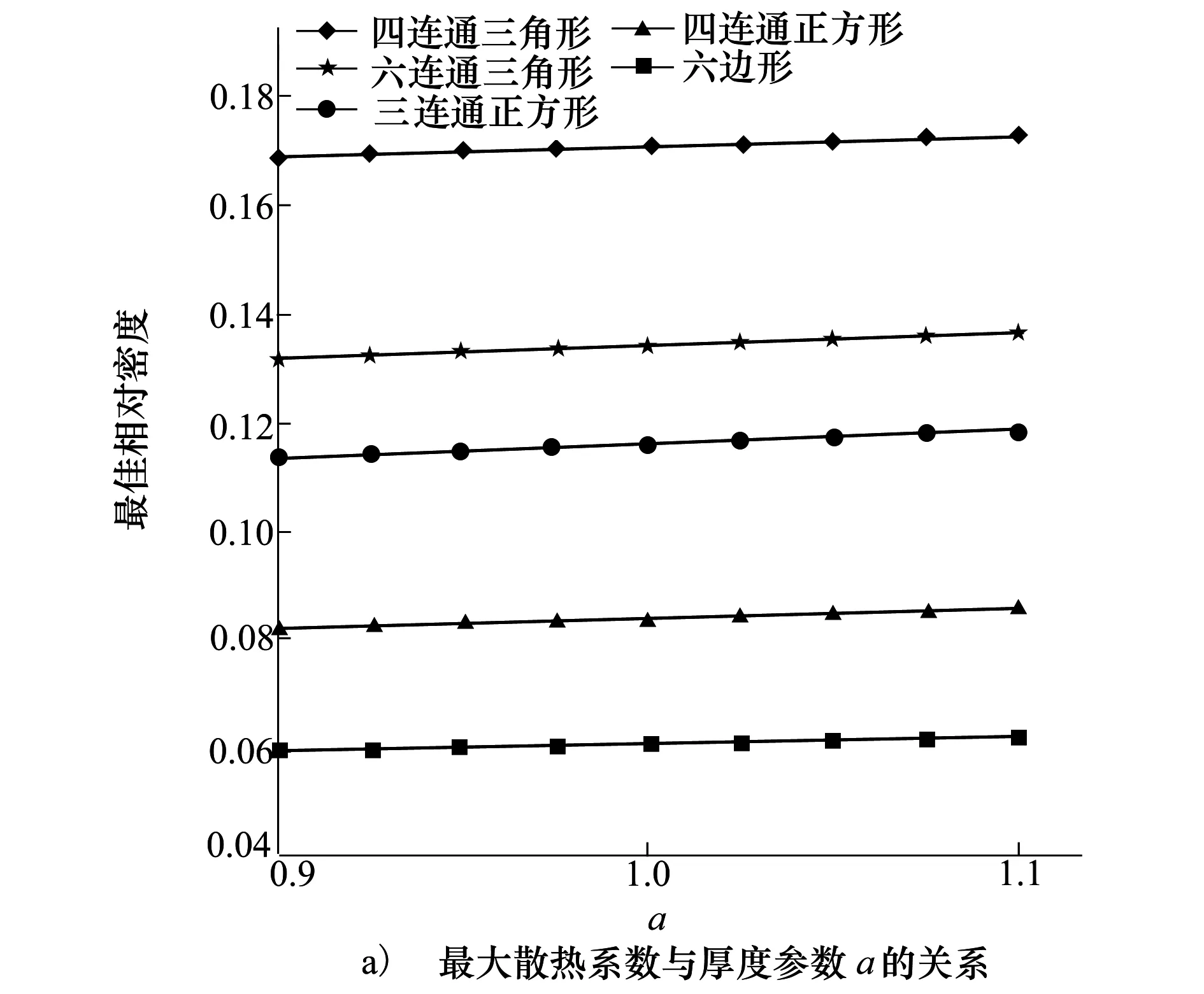
圖5 各種胞體構型的最大散熱系數和最佳相對密度與厚度參數a的函數圖

4 結 論

本文通過推導變厚度胞體壁多孔夾層材料散熱系數,研究了胞體壁厚度變化對多孔夾層材料主動散熱性能的影響。得到了以下結論:

3) 隨著厚度參數a的變化,三角形和正方形的最大散熱系數和最佳相對密度變化快,而六邊形的最大散熱系數和最佳相對密度變化慢。說明厚度的變化對六邊形單元的主動散熱能力影響小,而對三角形和正方形單元的影響大。

本文研究了變厚度胞體壁多孔夾層材料的主動散熱性能,為變厚度胞體壁多孔夾層材料的結構優化提供了理論支持,同時為三維金屬泡沫材料的主動散熱性能研究打下一定的基礎。