四軸飛行器串級ADRC軌跡跟蹤控制
胡文華,曹仁贏
(華東交通大學電氣與自動化工程學院,江西 南昌,330013)
四軸飛行器具有功能多樣、飛行靈活、能垂直起降的特點,在基礎設施建設、農業、能源、公共安全、新聞媒體等領域已獲得廣泛應用。從控制角度出發,四軸飛行器為欠驅動、強耦合、非線性的復雜系統,難以精確建模,同時易受外部環境的干擾。四軸飛行器最傳統的控制方法是PID控制。文獻[1]在PID控制基礎上加入限制積分飽和的模塊,以避免系統產生超調,但外部干擾會影響飛行器的穩定性;文獻[2]針對姿態角速率、姿態角分別設計內環LQR(線性二次型調節器)控制以及外環PID控制的雙回路閉環控制器,改善了系統的控制性能,但LQR本質上依然是線性控制,模型不確定對其控制效果有較大影響;文獻[3]采用魯棒控制,對外界干擾和負載不確定具有一定的適應性;文獻[4]采用自抗擾控制(active disturbance rejection control, ADRC)技術,并使用粒子群算法對ADRC參數自整定,既利用了ADRC的抗干擾性能,也解決了ADRC參數過多、整定費時、難以獲得最優解的問題,具有重要借鑒意義;文獻[5]采用有限時間反步控制并結合輔助輸入飽和補償器,避免了旋轉運動的奇異性;文獻[6]將反步法和滑模控制相結合,并將定位算法擴展到無人機中,提高了非線性控制器的控制性能。

1 四軸飛行器建模
通過動力學和運動學分析,根據牛頓-歐拉方程建立四軸飛行器的數學模型[7]:
(1)

(2)

2 串級自抗擾控制器設計
2.1 控制結構

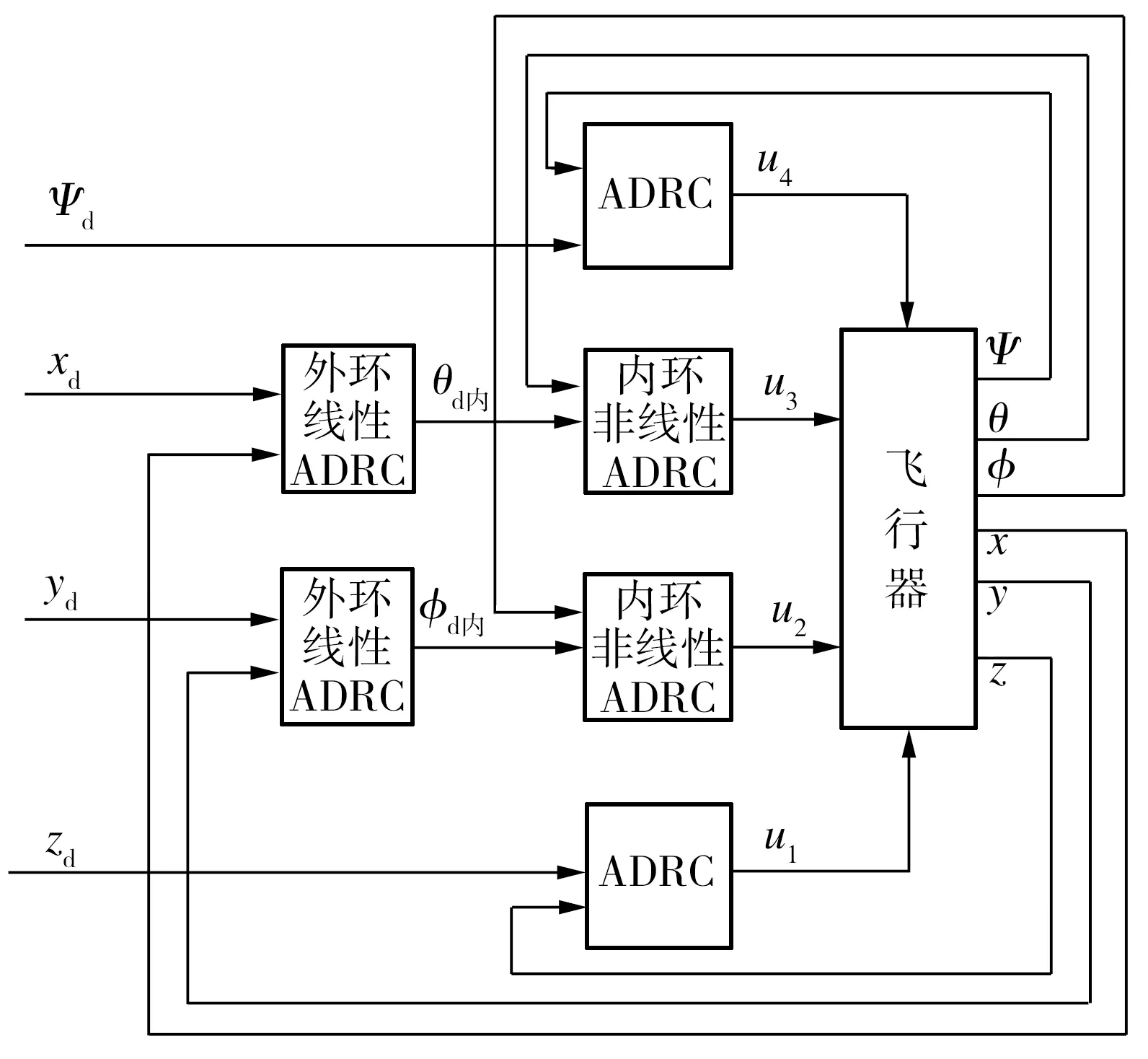
圖1 四軸飛行器串級自抗擾控制結構
2.2 非線性自抗擾控制器原理
非線性ADRC由跟蹤微分器TD、擴張狀態觀測器ESO、非線性狀態誤差反饋律NLSEFCL三部分組成。本文設計的內環非線性ADRC的基本結構如圖2所示。

圖2 內環自抗擾控制結構
(1)二階跟蹤微分器TD
根據設定值vd安排過渡過程vd1,并提取其微分信號vd2。
(3)
式中:h為步長;h0為濾波因子;r決定微分器對輸入信號的跟蹤速度,稱為速度因子;fst是非線性的最速控制綜合函數,其一般形式為fst(x1,x2,r,h),定義如下:
(4)
(2)擴張狀態觀測器ESO
根據被控對象的輸入u、輸出w估計出被控對象狀態z1、z2以及對象受到的總擾動量z3。
(5)
式中:β01、β02、β03是大于零的參數,其選取原則可參考文獻[8];0<α1、α2<1,通常取α1=0.5,α2=0.25;b為常數;δ為fal函數線性區間寬度,fal函數定義為:
(6)
式中:α一般取值為0.5。
(3)非線性狀態誤差反饋律NLSEFCL
根據輸入到NLSEFCL中的誤差e1、e2以及ESO輸出的z3來決定被控對象的最終控制量u:
(7)
式中:fal函數定義和式(6)中的一致,但α取值不同。選取合適參數β1、β2,即可實現對積分串聯對象的非線性控制。
2.3 線性自抗擾控制器原理
線性ADRC由跟蹤微分器TD、擴張狀態觀測器ESO和線性狀態誤差反饋律LSEFCL三部分組成,其中TD和ESO與非線性ADRC的一致,而線性狀態誤差反饋律為:
(8)
式中:b1、b2分別為比例和微分系數;e1、e2、b的定義與非線性ADRC中類似;u為最終輸入到飛行器的控制量,通過控制無刷直流電機的調速器,調整旋翼槳葉的速度,即可對飛行器的飛行狀態進行控制。
3 改進粒子群算法
本文采用文獻[9]中的改進粒子群算法,該算法是在標準粒子群算法的基礎上,對速度更新公式中的慣性權重ω進行改進,根據粒子與全局最優粒子的距離動態改變慣性權重,同時引入雜交變異算子,增加迭代后期的粒子多樣性。
在標準粒子群算法中,慣性權重ω是一固定值,而改進粒子群算法中慣性權重的計算公式為:
(9)
其中,
(10)
(11)
式中:Lki表示第k次迭代后粒子i(最優粒子除外)與當前全局最優粒子的距離;Lki,max、Lki,min表示粒子i經過k次迭代后的最大和最小Lki值;Tmax為最大迭代次數;ωmax、ωmin為最大和最小慣性權重值。

適應度函數選取ITAE指標,其定義為:

(12)
式中:t為時間;e(t)為誤差。
改進粒子群算法的具體流程為:
(1)隨機初始化種群,包括50個粒子,每個粒子有4個維度,將其作為參數載入四軸飛行器Simulink仿真模型,得出適應度值,并選出個體的歷史最優和種群的全局最優;
(2)計算各個粒子與當前全局最優粒子的距離,更新下一次迭代過程中各粒子的慣性權重ω;
(3)更新每個粒子的位置和速度,并計算適應度值;
(4)若該粒子當前適應度值比其歷史最優值好,則用當前值取代歷史最優值;
(5)若該粒子歷史最優值比全局最優值好,則替代全局最優值;
(6)判斷是否滿足雜交條件即連續10代全局最優值保持不變,若滿足則執行第(7)步,否則執行第(8)步;
(7)從當前50個粒子中選取20個較優粒子雜交產生新粒子,替換舊粒子,轉到第(2)步;
(8)判斷是否達到最大迭代次數,是則輸出全局最優值,否則轉到第(2)步。
4 Simulink仿真
根據四軸飛行器數學模型和實驗室的四軸飛行器實際參數(見表1),采用Simulink軟件進行仿真實驗。
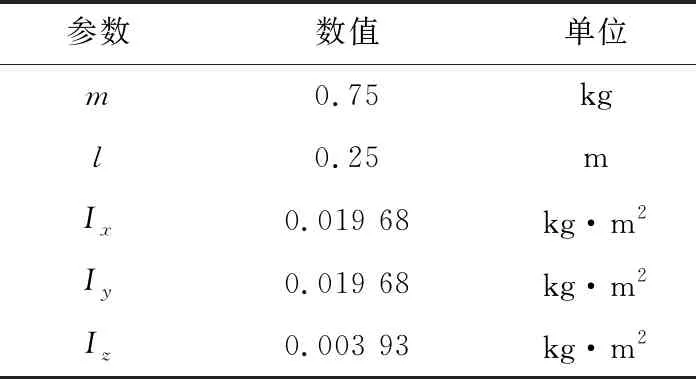
表1 四軸飛行器參數
4.1 飛行器定點懸停能力
為測試基于串級ADRC的四軸飛行器懸停能力,將飛行器初始位置定為原點O(0,0,0),設定其飛向指定的三維空間位置A(2,3,3.5),仿真結果見圖3。從圖3可以看出,飛行器在3 s內即可到達預設空間位置A,且超調量在3%以內。圖4為四軸飛行器的偏航角變化曲線,由圖4可知,Ψ通道僅靠單ADRC即可以獲得精確快速的偏航角控制。
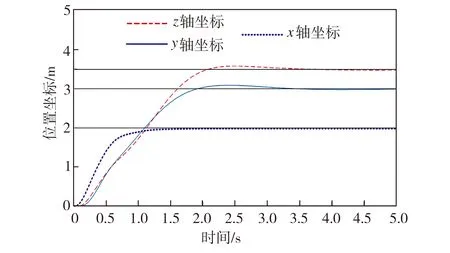
圖3 四軸飛行器的位置變化曲線

圖4 四軸飛行器的偏航角變化曲線
采用改進粒子群算法的參數優化曲線如圖5所示,適應度函數值的變化如圖6所示。從圖5、圖6中可知,改進粒子群算法收斂速度很快。
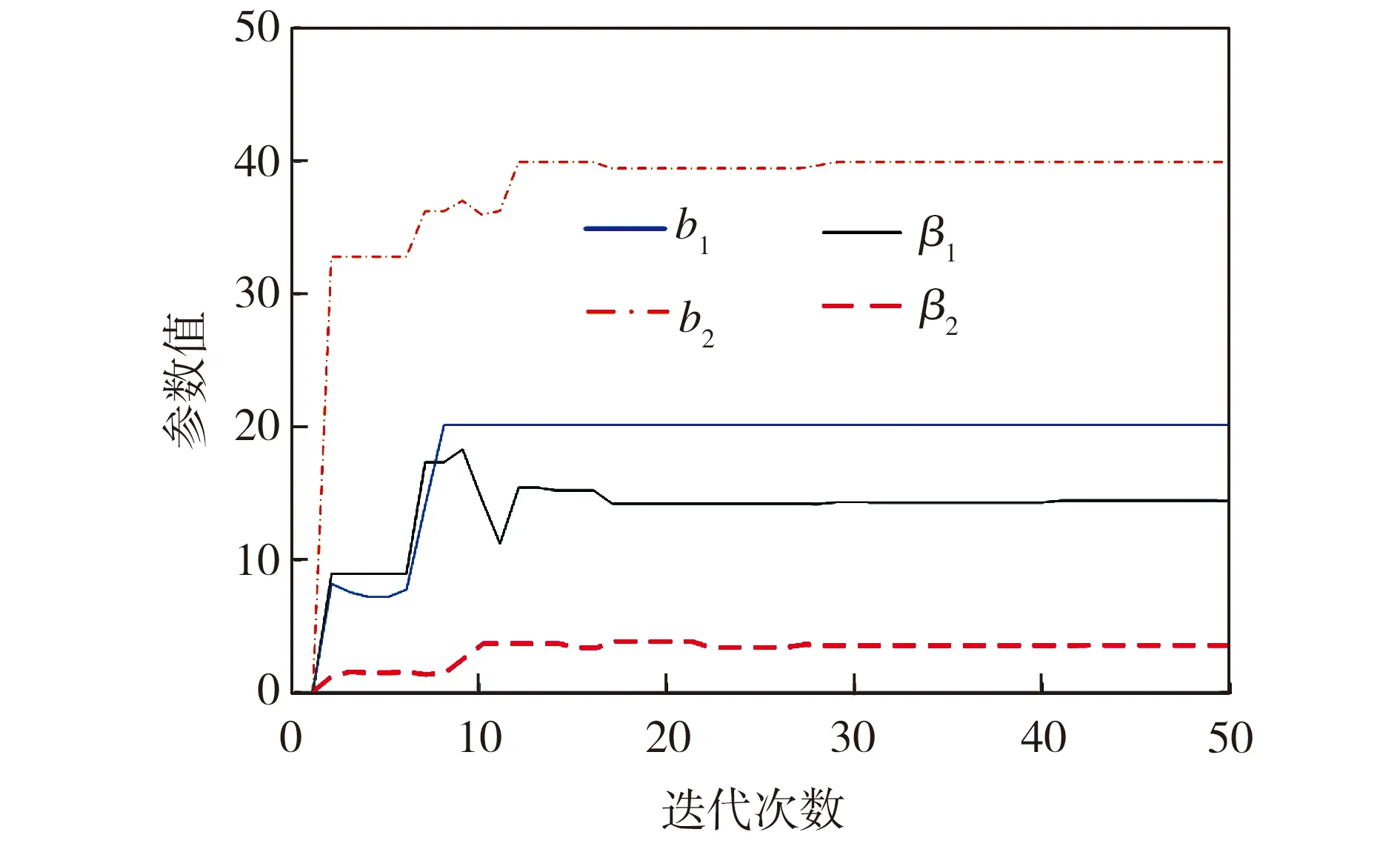
圖5 參數優化曲線
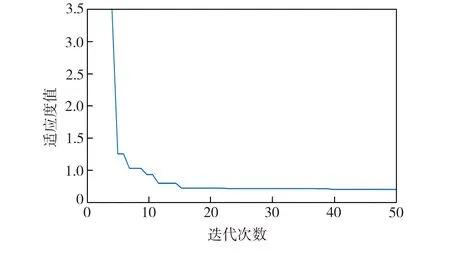
圖6 適應度值變化曲線
4.2 飛行器指令跟蹤能力
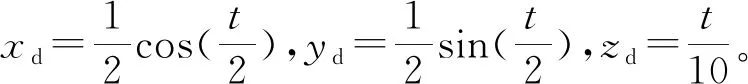
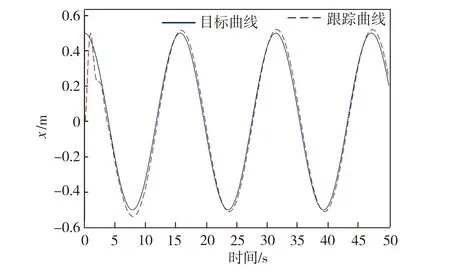
圖7 x軸軌跡跟蹤
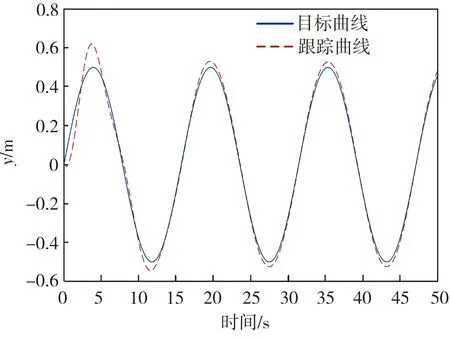
圖8 y軸軌跡跟蹤
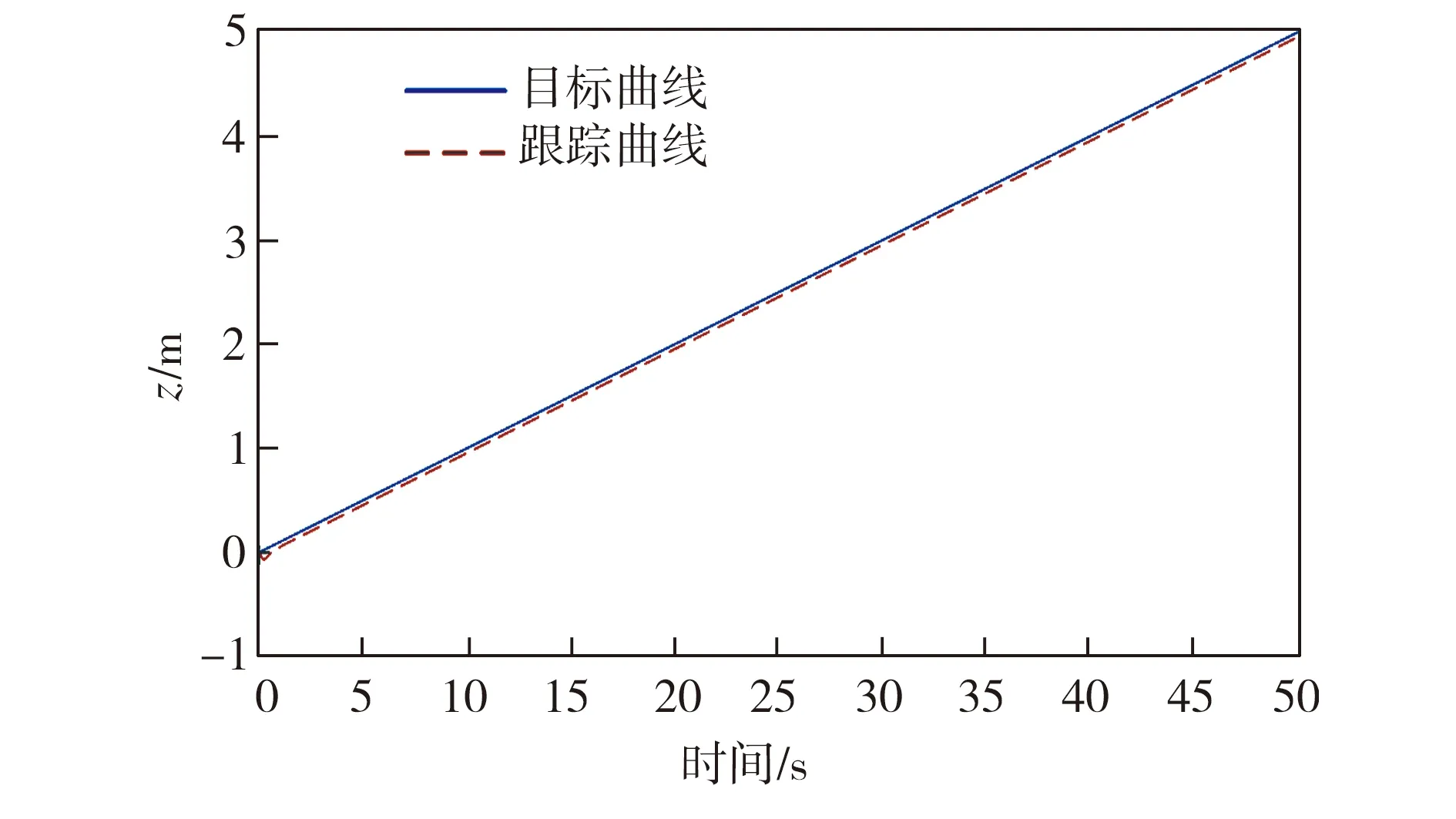
圖9 z軸軌跡跟蹤

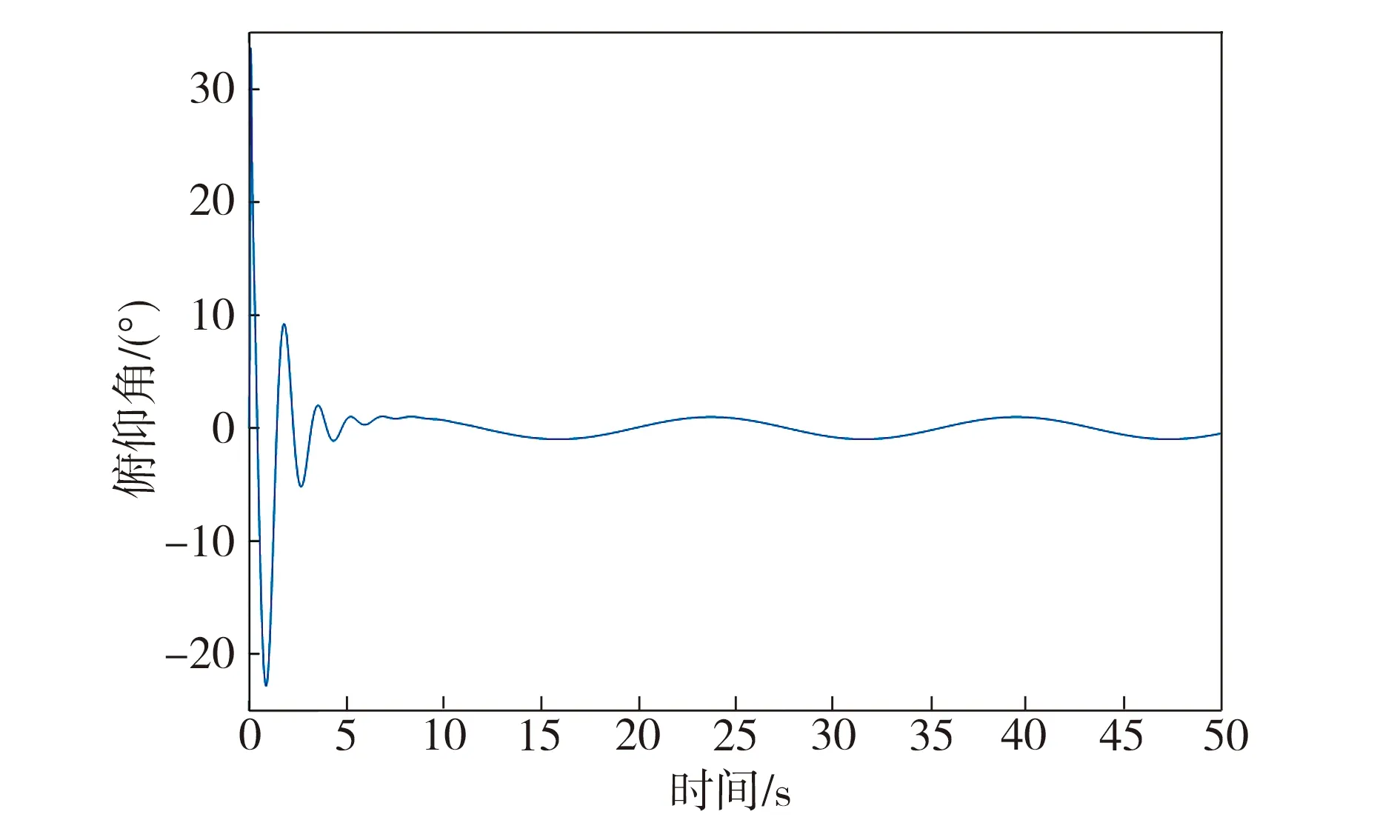
圖11 俯仰角變化曲線

圖12 翻滾角變化曲線
4.3 飛行器抗干擾能力

圖13 噪聲干擾
從圖14可以看出,在外部干擾下,基于串級ADRC的四軸飛行器軌跡偏離很小,可以忽略不計,而基于串級PID控制的飛行器產生較大的抖動,由此證明本文提出的串級ADRC的抗干擾性能優于串級PID控制,即具有良好的魯棒性。
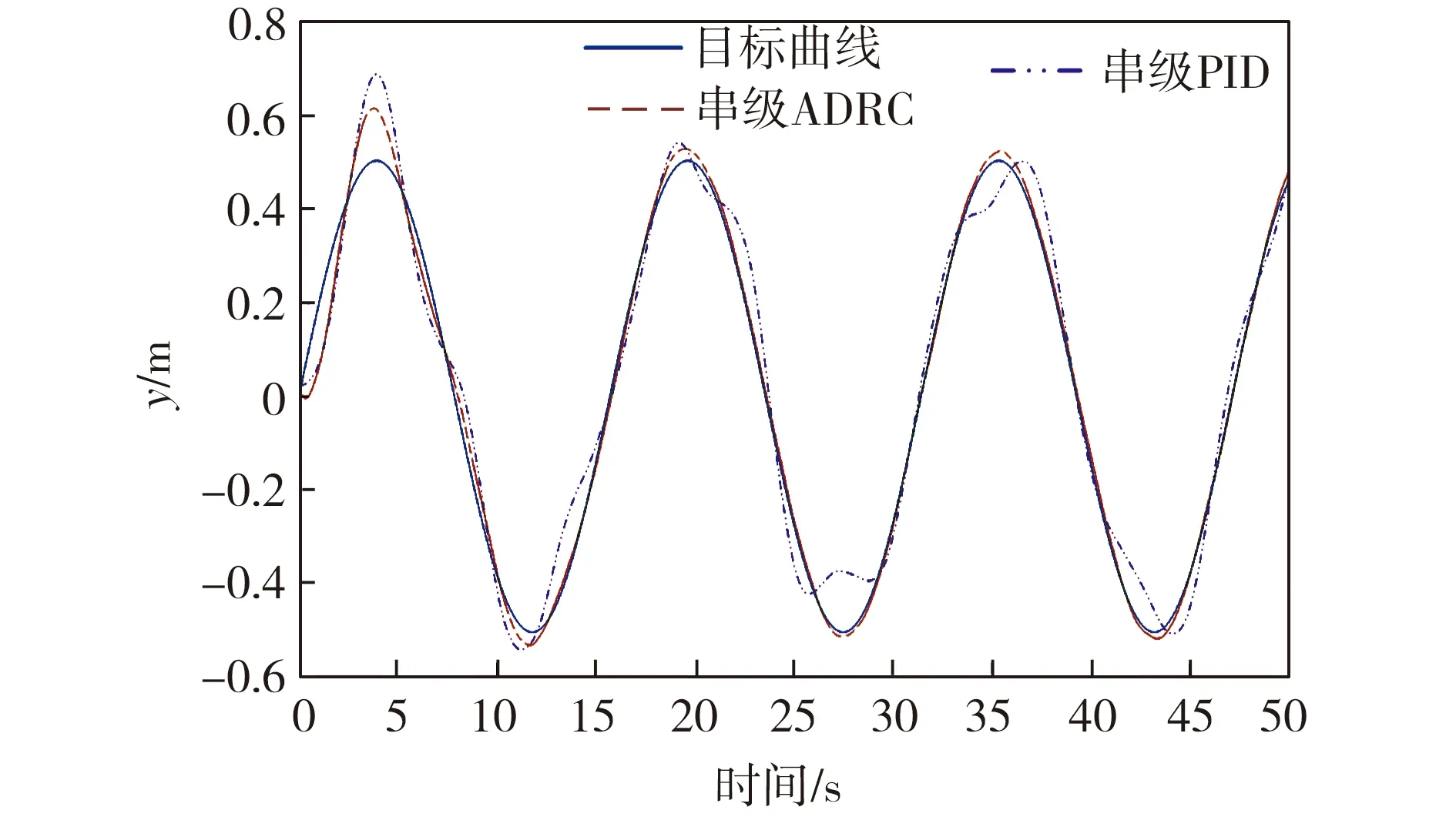
圖14 噪聲干擾下的四軸飛行器軌跡跟蹤
Fig.14 Trajectory tracking of quadrotor subjected to noise interference
5 結語


