混沌理論支持下的橋梁變形監測研究

許章平，欒元重，劉中華，崔騰飛，相 濤

(山東科技大學測繪科學與工程學院，山東 青島 266590)

大橋在人們生活中扮演著重要的角色，跨海大橋更是為人們的出行提供了方便。它處在海洋之上，不僅經受海水的沖擊，還承受著車載的外力，發生形變后如果不進行充分的維護，就會影響橋體的使用，嚴重時會危及橋身的安全，引起坍塌，給社會和人類的生活帶來極大的損失。因此，隨時監測橋體的變形狀態，并及時維護，不僅能保證橋身的正常運行，還能降低國家和人民的經濟損失。由于橋梁的變形受很多因素的影響，使用傳統的預測模型，難以精確判別橋梁變形程度。針對橋梁形變的非線性特點，需要使用非線性的預測模型進行分析。

非線性混沌時間預測是當今科學與工程技術領域研究的熱點，但在變形分析方面的認識還不夠深入，需要研究和解決的問題較很多[1]。因此，開展針對跨海大橋應用混沌理論進行時間序列預測的研究，深入了解并探尋大橋的變形規律，可為橋梁的維護和安全運行提供科學數據，對揭示跨海大橋變形機理、實現橋梁安全運營具有重大意義。本文對青島膠州灣跨海大橋開展變形監測工作，在傳統數據處理的基礎上，進行非線性、動態的測量數據處理，并通過建立加權一階局域預計模型和RBF神經網絡混沌預計模型對其進行預測研究。

1 時間序列的相空間重構

混沌系統形變軌跡經過長時間不斷的變化，具有一定的規律可循。這種軌跡經過多種變化，變成一種與時間有關的序列時會呈現出混亂的特性。由于系統元素是相關的，因此所產生的數據點也是互相關聯的。文獻[2]提出使用原系統中的某個變量的延遲坐標進行相空間重構；文獻[3]證實了可以找到合適的嵌入維數，即若延遲坐標的維數是動力系統的維數，在該嵌入維空間之中可以把這個有規則的軌跡還原出來，從而為混沌時間序列的預測理論打下基礎。相空間重構的核心是延遲時間和嵌入維數的求取，傳統的C-C算法和G-P算法能夠準確求出重構參數[4-6]，但這兩種算法存在著不足之處。針對這些不足，本文使用改進的C-C算法和G-P算法，能夠更好地完成相空間重構，可為后續預計模型的建立提供方便。

1.1 傳統C-C算法原理

C-C算法是應用關聯積分構建時間序列的檢驗統計量來代表非線性時間序列的相關性，最終求取嵌入維數的計算方法。定義檢驗統計量，N為時間序列長度[7-8]，即

S1(m,N,r,t)=C(m,N,r,t)-Cm(1,N,r,t)

(1)

將時間序列分解為t個子序列，t為重構時延，當N→∞時，將統計量采用分塊策略可表示為

(2)

求取最大與最小兩個半徑r的差量如下

ΔS(m,t)=max{S(m,rj,t)}-min{S(m,rj,t)}

(3)

(4)

(5)

(6)

1.2 C-C算法的改進

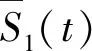
(7)

式中，Xn,s和xn,s分別為X和x的n個無重疊子集，n為常數，它可以控制計算精度和速度。當n=1時,S1(m,N,r,t)的計算精度最高；當n較大時，會存在一定的誤差，但不同的時間之間只相差一個常數，因此不影響局部極值的讀取。

1.3 傳統G-P算法原理

G-P算法從時間序列中計算吸引子的關聯維數，對實測數據x(1)，x(2)，…,x(t)用Tankens嵌入維定理進行延時重構[9]，得到一組空間向量X(t)=(x(t),x(t+τ),…,x[t+(m-1)τ])，t=1,2，…,M，其中M=N-(m-1)τ,對于空間中的M點，計算有關聯向量的對數。間距小于指定正數r的向量都是關聯向量，向量的距離一般有兩種表示方法：2-笵數與∞-笵數，這里選用∞-笵數來計算，即將兩向量最大分量作為距離。它在M2種可能中，配對所占的百分比稱為關聯積分

(8)

式中，θ(·)為Heaviside單位函數，即

(9)

由此可計算關聯積分Cr(r)，選擇不同鄰域半徑r，并分別對Cr(r)進行計算，然后擬合出Dm，增加m，最后得出飽和值D，根據m≥2D+1求出恰當的嵌入維數m[10]。

1.4 G-P算法的改進

傳統G-P算法存在4個問題：①尋找鄰域半徑r時，個人主觀性很強，若r取值太小，則鄰域內相位點太少，Cr(r)趨近于0，若r取值太大，則會包含所有的相位點，此時Cr(r)趨近于1，給嵌入維數的判別帶來困難；②主要依賴人的觀察來判別無標度區間，選取個人認為的線性區域，然后判別該區域線段的導數是否變化，這種主觀占決定因素的判別容易產生誤差；③鄰域半徑r變化步長的選擇，步長太大，樣本點數會變少，影響精度，步長太小，不僅增加運算量，同時也放大了噪聲誤差；④求取關聯積分的方法在原理和結構上存在冗余，若不進行改善，不能滿足實用性需要。

針對以上幾個問題，本文采用以下方法進行改進：①鄰域半徑r的選擇范圍應該在相點間距的最小與最大的數值之間；②選定[ln(σ/3),ln(3σ)](σ為時間序列的標準差)為無標度區間的界限，找出Dm和m的函數關系，并畫出關系曲線圖，當曲線斜率趨近于0時，說明Dm趨于飽和；③步長從0開始線性遞增，進行多次嘗試；④在原始數據中讀取相點的多維元素來計算相點間距離，不再進行多次重構，可以減輕大量的計算任務，當嵌入維數確定以后相點間距離不受r的影響，由于循環計算造成計算冗余，因此每進行一次相點距離的計算便與r進行一次比較，根據如下遞推公式可以減少大量計算工作

(10)

2 時間序列混沌識別

運用小數據量法求取最大Lvyapunov指數，小數據量法基本原理[11]為：根據重構的混沌時間序列的相空間，查詢給定軌道上每個點的最小間距的鄰點，即

(11)

通過計算所有相鄰最近兩點的平均發散率的估算值獲取最大Lyapunov指數，即

(12)

式中,m為常數；Δt為樣本周期；dt(i)為第t組相鄰最近的兩點經過i個離散時間的步長距離。對dt(i)取對數得

lndt(i)=lnCt+λ1(iΔt)t=1,2,…,M

(13)

最大Lyapunov指數可通過近似于式(13)中直線的斜率獲得。

3 混沌時間序列預測

3.1 加權一階局域預測模型

在相空間之間計算每個鄰域點到X(t)之間的歐氏距離，并找出X(t)的參考向量集X(ti),i=1,2,…,N，且點X(ti)與X(t)的區間為d，假設dm為di中的最小量，定義點權值為[12]

(14)

式中，a為常系數，通常取a=1。則一階局域線性擬合為

X(ti+1)=aR+bX(ti)i=1,2,…,N

(15)

式中，R=[11…1]T。嵌入維數m=1時，采用加權最小二乘法，有

(16)

對式(16)中與a、b有關的函數求偏導，并求解a和b，代入可以求取預測值如下

X(ti+1)=aR+bX(ti)

(17)

3.2 神經網絡混沌預測模型

徑向基函數RBF神經網絡將前饋網絡分為3層：第1層為輸入層，由信號源節點組成[13]；第2層為隱含層，將輸入空間投影到新的空間，根據問題的需要確定單元數；第3層為輸出層，對輸入模式的作用作出反應[14]。

RBF網絡進行投影f：Rn→Rm，其數學表達式為

(18)

(19)

式中，β表示寬度值，為常數。

RBF神經網絡混沌預測的步驟為[15]：

(1) 對時間序列進行歸一化處理，所得數據分為預測部分和訓練部分；利用時間延遲和嵌入維數m兩個重構參數對訓練部分進行相空間重構，重構后的點數為N=n-(m-1)。

(2) 通過調用newrb函數建立徑向基神經網絡的預測模型，其格式為net=newrb(P,T,goal,SPERAD,MN,DF)，其中，P為輸入向量，m個輸入層元素；T為目標向量；SPREAD為隱含層的分布密度；指定元素的最大數目為MN；DF為兩次顯示時間間隔內所增加的神經元數量。newrb函數內部確定線性變換及非線性變換、初始偏離值與初始值。用RBF網絡逼近函數時，newrb可以自動添加網絡中的隱層神經元，當均方誤差滿足限差時停止，此時所用的網絡輸出為an=sim(net,P)。

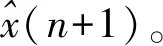
3.3 預測模型評價

預測過程中存在多種不確定因素，若預測結果不科學，建立的模型就不能用在橋梁變形數據處理中，因此需要采用科學的評價標準進行評定。評定的方法有很多種，本文采用以下兩種方法：

(1) 平均絕對誤差(MAE)：計算每期實際值與預測值絕對誤差的平均值，公式如下

(20)

(2) 均方根誤差(RMSE)：求取絕對誤差平方和的平均值，然后將平均值進行開方，計算公式如下

(21)

式中，y(i)為第i點的預測值；x(i)為第i點的實測值；n為期數。

4 應用實例

本次觀測高程基準網共布設7個控制點，其中3個已知的基準點。根據《國家一、二等水準測量規范》(GB/T 12897—2006)規定的二等水準測量要求對青島膠州灣大橋的高程基準網進行觀測。采用精度為0.6 mm的Trimble DINI03數字水準儀及配套銦瓦條碼尺，按“后前前后”奇偶交替模式對青島膠州灣大橋進行往返觀測，數據合格后取其平均值作為項目實測數據，確保變形數據的可靠性。從2017年4月—2017年10月期間連續檢測的數據中每3 d取一期形成等間隔的時間序列，共70期數據。下沉值計算均以第1期觀測數據為基準。以沉降點R6為例，下沉數據如圖1所示。

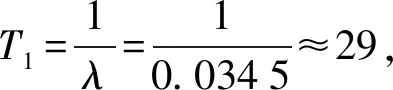
本文運用兩種混沌時間序列預測方法對跨海大橋沉降數據進行預計：①根據時間延遲τ=0和嵌入維數m=10對時間序列進行相空間重構，建立加權一階局域預測模型[17]；②對時間序列進行歸一化，取前60期數據作為訓練樣本，再根據前面所求的時間延遲和嵌入維數進行相空間重構，建立RBF神經網絡混沌預測模型[18]；③使用以上兩種混沌預計模型及系數為0.9和0.5的指數平滑法對時間序列進行短期預測。系統最長預報時間為87 d，為保證預測精度，預測數據選取后30 d觀測的最后10期數據對比分析預測結果。如表1和圖9所示。

由表1可以看出，混沌時間序列預測結果比指數平滑預測結果更接近實測值，說明混沌時間序列預測方法的可靠性；RBF神經網絡混沌時間序列預計效果優于加權一階局域法預計效果。由圖9可知，兩種模型預測結果都與真實值相差不大，且隨著期數的增加，兩種模型預計值與實測值的差距越來越大，預測誤差隨著預測時間的增加呈遞增趨勢，但最大相對誤差為11%，說明混沌預測法在橋梁變形監測中進行短期預測是可行的。

表1 兩種模型預測結果對比

對以上3種模型的預測精度進行評定，結果見表2。

表2 3種預測模型精度對比

從表2中定量數值可看出，加權一階局域法和RBF神經網絡混沌法預測精度明顯高于指數平滑法，RBF神經網絡混沌法計算精度優于加權一階局域法，表明混沌時間序列預測方法可靠，能夠反映橋梁變形的真實狀態。

5 結 論

本文根據青島膠州灣跨海大橋的變形監測數據，提出了橋梁變形混沌狀態判別標準，給出了橋梁變形混沌相空間重構方法；并綜合神經網絡非線性數據處理的能力，建立了橋梁變形神經網絡混沌時間序列預計模型。結論如下：

(1) 采用改進的C-C法計算時間序列的時間延遲τ，采用改進的G-P法計算最佳嵌入維數m，通過這兩個重構參數，對橋梁實測數據進行了相空間重構，實例表明與傳統算法相比，改進算法的抗干擾性、計算效率等方面都得到了改善。

(2) 建立了混沌預測模型，將混沌預測方法預測精度與指數平滑法預測精度進行比較，前者預測精度明顯高于后者，RBF神經網絡混沌法預測精度優于加權一階局域法。