基于CRITIC-有限區間云模型的邊坡穩定性評價*

王加闖,黃明健,2,過 江

(1.中南大學 資源與安全工程學院，湖南 長沙 410083； 2. 湖南漣邵建工(集團)有限責任公司，湖南 長沙 410011)

0 引言

近幾年基建設施規模日益完善,邊坡穩定性成為建設過程中比較重要的一環，其穩定性評價成為決定工程施工成敗的重要因素。影響邊坡穩定性的因素的不確定性、危險性等級分級標準的不確定性以及影響因子權系數求取的不確定性，這些使得邊坡的穩定性等級分類和工程治理充滿著不確定性。為此學界專家學者基于這種不確定性問題提出了多種理論來探討邊坡的穩定性。

宋盛淵等[1]利用突變理論模型剖析了邊坡系統的內在機制；胡軍等[2]提出了BP神經網絡的耦合模型；戴興國[3]、閆長斌[4]構建了邊坡穩定性評價的距離判別賦權模型,彌補了馬氏距離法忽略指標重要性存在差異的缺陷；楊文東等[5]根據指標隸屬不同穩定性等級的特征建立了巖質邊坡穩定性的云模型評估方法；趙軍等[6]基于實際評價指標的綜合信息量,提出基于改進的熵權計算權重方法的云模型評價模型。這些理論和模型在一定程度上完善了邊坡穩定性的評價體系,但由于影響邊坡穩定性因素的復雜性,仍難以克服自身存在的缺陷:突變理論模糊數學模型沒有考慮指標權重,只是衡量了指標的相對重要性,仍然摻雜著人為主觀性；可拓模型仍采用了主觀賦值權重的方法,在計算過程中會忽略一些重要的約束條件；耦合的神經網絡算法計算復雜,獲取的樣本代表性不強,擬合速度難以控制；距離判別賦權模型對樣本數據依賴性強。

本文引用結合實際評價指標服從均勻分布和正態分布的有限區域云模型[7]。傳統的云模型在邊界為單邊區間時即形如[0,C]或[C,)區間時,其邊緣的指標分布仍如傳統正態分布一樣,這種理論下的模擬結果,往往會和實際情況存在偏差,因此引入了有限區間的云模型；運用CRITIC算法[8]計算指標權重,可以考慮各指標間的相關性,使計算結果更具有準確性。

1 云模型理論

云模型是由李德毅等[9]提出的一種處理模糊問題的概念模型,其是從隸屬度的角度出發處理數據的模糊性和隨機性。現已應用于生產生活的多個領域,并取得了良好的效果[10-11]。

1.1 云的基本概念

云模型是利用3個數學符號表示的不確定關系,進而進行定性與定量轉化的一種模糊模型[9]。傳統的云模型通常處理的是指標分布近似趨于正態分布,但在工程實踐中，傳統的正態云模型很難正確的描述出模擬對象的特征，故本文采用經修改的有限區間下的云模型。

設U是一個精確數值表示的定量集合,其中,U={x},C是U上的定性概念,若存在任意的定量元素,且x存在1個穩定傾向的隨機數μ(x)=(0,1)在定性概念C上的1次隨機實現,其中[12]:

μ:U→[0,1],?x∈U,x→μ(x)

(1)

則x在集合U上的分布稱為云,每1個點(x,μ(x))稱為1個云滴。

1.2 數字特征

通常云模型概念的支撐,主要用3個基本云模型數字特征值加以表述,即期望Ex、熵En、超熵He[9]。期望Ex代表了定性概念的中間位置,決定了云滴分布的位置；熵En表示在論域區間被定性概念表述的云滴的取值范圍,反映了基本概念的模糊性和隨機性；超熵He,也就是熵的熵,表示熵的不確定性,在云圖中,通常表示云的厚度,超熵越大,云越厚。

(2)

(3)

(4)

(5)

(6)

(7)

同理亦可求出指標值越大,等級區間越小型指標屬于等級k的左、右半區間長度:

(8)

(9)

1.3 云發生器

正向云發生器是云模型從理論到實際應用的關鍵,是利用云特征參數N(Ex,En,He)產生云滴即P(xi,μi)(i=1,2,3,…,n),進而將定性分析向定量計算的轉化過程；以正向云發生器為載體，利用云模型特征參數,結合指標等級特征和想要生成的云滴數N(本文取N=5 000),通過Matlab編程即可進行擬合。當指標處于兩端等級云均值之間的區間里時,該數學概念模型可以有如下定義:設U是1個精確數值表示的定量集合,其中,U={x},C是U上的定性概念,存在任意的定量元素x,且x存在1個穩定傾向的隨機數μ(x)=[0,1]在定性概念C上的1次隨機實現。若x滿足:x～[Ex,En2],x服從在特定有限區間里的正態分布,即x對C的確定度滿足:

(10)

當指標遠離期望Ex,此時x服從確定度為1的均勻分布。綜上所述，x服從的分布為式(11),本文kmax=5:

(11)

2 有限區域云模型和改進CRITIC法賦權模型的構建

所謂權重,是指在評價過程中,影響問題因素的重要程度,這種重要程度可以通過定性概念描述,也可以用定量數值表示。定性描述的權重充滿著主觀性,因此在實際生產中的指標權重,通常會用具體的算法表示。傳統求權算法通常只考慮指標信息量大小忽略了指標的相關性，因此本文主要采用另一種客觀賦權法—CRITIC算法[8]。

2.1 邊坡穩定性評價計算框架及流程

1)根據眾多學者和地質研究人員的邊坡穩定性分析工作,建立滑坡評價指標的危險性等級劃分標準;2)求出分類指標的云特征參數利用云發生器繪制云滴圖,生成云模型；3)根據樣本實測數據計算各指標對應的各級別確定度；4)利用改進的CRITIC算法計算各指標權重；5)計算綜合權重值,按照最大隸屬度原則確定邊坡危險等級。

圖1 傳統云模型與有限區間云模型Fig.1 Traditional cloud model and finite interval cloud model

圖2 邊坡穩定性評價流程Fig.2 Procedure of slope stability evaluation stability evaluation flow chart

2.2 CRITIC法賦權算法

CRITIC算法是由Diakoulaki[15]在1995年提出的一種客觀賦值法。這種方法通常用以下2個量來反映:指標間的相關系數及指標內的變異大小。通常相關系數越大,指標間的沖突性越小,體現的信息量重復性越強,指標所占權重也就越小；指標內的變異大小,通常用指標變異性進行量化,用指標的標準差來衡量,標準差越大,對象之間的差異就越大,指標所占權重就越大。

基于以上2個量,不難看出,基于CRITIC算法所得到的權重大小,既考慮了評價指標間的相關性,又考慮了評價指標內的變異性,即體現的信息量,因此,優越于信息熵算法只考慮指標信息量大小,所得權重也更加準確、客觀。設評價對象m個,評價指標n個，其主要步驟如下[9]:

1)利用初始數據,建立預測樣本指標數值矩陣:

X=(xij)m×n

(12)

式中:xij為第i個評價對象第j個指標所對應的原始數值。

2)根據Z-score方法,對式(12)矩陣X中的指標值進行標準化處理:

(13)

根據該算法,上述公式中2個參數:

(14)

3)求指標的變異系數：

(15)

式中：vj為第j個指標的變異系數。

4)利用步驟2)得到標準化矩陣X*,利用統計學概念計算相關系數,得到相關系數矩陣:

R=(rkl)n×n,k=1,2,…,n;l=1,2,…,n

(16)

式中：rkl為第K個指標和第l個指標間的相關系數。

5)求各指標表示獨立性程度的概念—量化系數:

(17)

6)計算各指標綜合信息量:

(18)

7)確定各評價指標權重:

(19)

2.3 綜合權重的確定

經過以上步驟的展開和計算,我們可以得出不同評價指標實測數據x隸屬于某云滴確定度μ(x),再結合CRITIC算法算出不同評價指標的權重,則最終的綜合確定度公式:

(20)

式中：μk,j為樣本的第j個指標的實測值所在k的確定度；ω(Ej)為樣本第j個評價指標所占權重大小。

根據最終的綜合確定度,按照最大隸屬度原則,確定樣本的隸屬等級:

L=max(μ1,μ2,μ3,…,μk)

(21)

3 工程實例

3.1 評價指標的選取

邊坡的穩定性受自身的復雜特點和工程技術的影響,最主要的因素主要包括邊坡所在位置的地質地貌、水文結構和外部環境如人類的生產活動、地質災害、降水量等。到目前為止,決定邊坡穩定性的因素,在學界和地質工程界并沒有統一標準。根據建立的分級標準應滿足代表性、關聯性、易量化、易獲取和存異性5個原則,參考相關文獻[13],特選定單軸抗壓強度(Rc)X1、彈性模量(Em)X2、泊松比(μ)X3、巖體結構特征(RQD)X4、巖土黏聚力(C)X5、內摩擦角(φ)X6、日最大降雨量X7、最大地應力X8、地下水狀態X9、邊坡高度X10、邊坡角X11和巖體聲波速度X12為評價因子。

由于邊坡穩定性影響因素的隨機性和模糊性會隨著時間和環境的變化而改變。分級標準的基礎通常與巖質邊坡的實際情況、不連續的地質情況有關。一般情況下,由于工程背景的不同,許多潛在因素也會對實際工況產生影響。結合文獻[16]露天采場的實際情況,參照工程巖體分類標準將邊坡分為5個等級,分別為極穩定(Ⅰ)、穩定(Ⅱ)、基本穩定(Ⅲ)、不穩定(Ⅳ)和極不穩定(Ⅴ)。具體指標的分類標準見表1，邊坡指標實測值見表2。

3.2 云滴圖的生成

根據有限區域云模型理論和分級標準,依據式(2)～(9)確定云特征參數,生成云滴圖如圖3所示。橫坐標表示評價指標,縱坐標表示不同取值的評價指標所確定的確定度,即隸屬度。

根據2.1節的計算方法,利用改進的CRITIC算法進行計算,根據公式(14)可計算出各指標的均值和方差,同時利用式(15)求出變異系數,根據初始指標的實測值,計算出標準化后數據所對應的指標之間的相關系數,利用式(19)可求出各評價指標的權重，如表3所示。

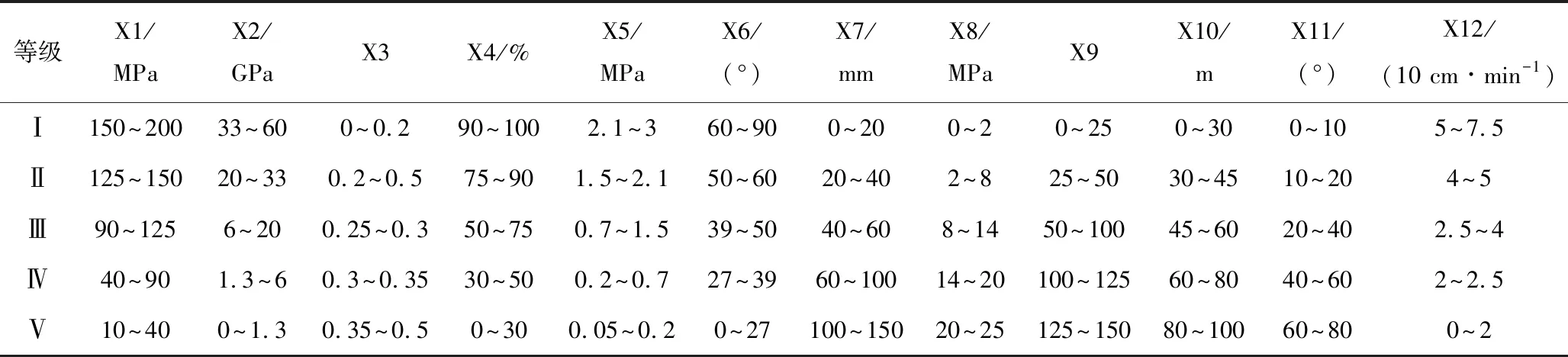
表1 單因素邊坡穩定性評價指標Table 1 Single factor evaluation indexes of slope stability

表2 指標實測值Table 2 Measured values of indexes

圖3 評價指標隸屬于各級別的云滴圖Fig.3 Cloud droplet graph of evaluation indexes attaching to each level

評價指標X1/MPaX2/GPaX3X4/%X5/MPaX6/(°)X7/mmX8/MPaX9X10/mX11/(°)X12/(10 cm?min-1)指標權重0.0500.0690.1400.020.0890.1450.0010.1200.0370.1830.1340.013

3.4 預測結果及分析

基于CRITIC算法和有限區域下云模型的計算模型,根據式(2)～(4)求出的云模型特征參數,進而結合云圖和正態云發生器,可計算出實測值隸屬于不同級別的隸屬度,帶入式(20)中,按照最大隸屬度原則,可求出不同樣本的最終穩定性級別。以第1個樣本第1項評價指標為例即單軸抗壓強度,實測值為X1=52.6 MPa,根據有限區域云模型計算公式和正向云發生器,可以求出該實測值隸屬于不同的評價等級分別為μ1=μ2=0,μ3=0.001,μ4=0.829,μ5=0.006。根據所求確定度數值,單從第1個樣本的單軸抗壓強度可以得知,該露天礦邊坡穩定性隸屬于第Ⅳ等級,隸屬于第五等級有很小的可能性,有非常小的可能隸屬于第Ⅲ等級,但是不可能隸屬于Ⅰ，Ⅱ等級,這與事實比較符合。因此可以結合式(20),根據最大隸屬度原則,計算出不同邊坡所在的危險等級,分級結果及對比見表4。

根據最終權重結果和確定度分析,相對于其他方法[16],基于CRITIC算法的有限區域云模型方法相對保守。樣本1，3，4危險性等級處于第Ⅲ等級,即基本穩定狀態,但是樣本1和樣本4對于等級Ⅳ有一定的傾向性,可以對邊坡的治理和防護提供一定的參考；樣本2根據最大隸屬度原則,該樣本危險性處在第Ⅳ等級,即不穩定狀態,根據實測數據可知,相對于其他樣本,樣本2的X6(內摩擦角)因素較大,而且根據權重計算,該影響因素所占權重較大,因此對邊坡的穩定性有一定的影響。對于不穩定樣本和有不穩定傾向的樣本應該采取一定的防護措施,如使用錨索和噴射混凝土加以牢固,或者利用網格梁支護等措施進行處理,做好邊坡穩定性工作的預防工作,防止發生危險事故。

表4 分析結果及比較Table 4 Analysis results and comparison

4 結論

1)利用CRITIC算法計算權重,選取某銅礦山露天邊坡,經對實測數據關聯度的計算,提高了評價指標權重的準確性。根據最終評價結果分析,利用該算法不僅可以進行安全現狀評價,也可以在得到危險性等級的同時,了解樣本危險性等級的傾向性,達到安全預測的目的。

2)針對邊坡穩定性評價的不確定性,選取某銅礦山露天邊礦的4個剖面,著重選取了12個影響邊坡穩定性的不安全因素(評價指標),使得評價結果更為合理,評價指標體系更加完善,提高了評價的可信度。

3)根據傳統正態云模型,結合改進的有限區域云模型,使評價指標的隸屬度更加合理準確,彌補了傳統模型下理論分布與實際部分不符的情況,擺脫了傳統理論模型下模擬結果可能超出實際范圍的風險；同時結合CRITIC求權算法,使得模擬結果與實際情況更加符合。結合多種分析方法可知,該方法預測結果相對準確,對分析露天礦邊坡穩定性問題提供了可行的定量分析方法。